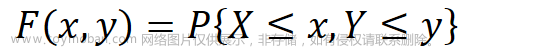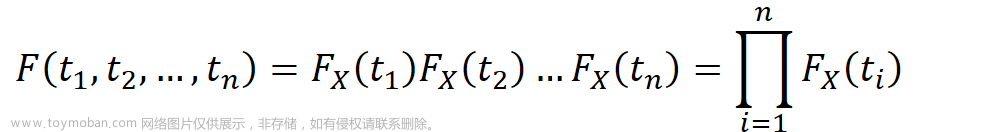概率论
第01回:一些基本概念
1. 随机试验
满足下列条件的试验称为随机试验.
- 可以在相同的条件下重复地进行;
- 每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果;
- 进行一次试验之前不能确定哪一个结果会出现.
2. 样本空间
我们研究随机现象的方法其实就是利用已知找到规律来分析未知,既然随机试验的所有可能结果我们都能事先知道,那我们先把这些结果列出来。
- 样本点:随机试验的每一个可能结果称为一个样本
- 样本空间S:所有样本点全体组成的集合称为样本空间
3. 随机事件
随机现象往往是通过一个具体情况或具体事件出现的,比如“扔色子扔出的点数是偶数”这个事件,相当于给扔出的点数有附加了一个条件,它的所有可能结果写欣集合内{2,4,6},我们会发现这个集合是样本空间的一个子集。
- 随机事件:样本空间S的子集称为随机事件,通常用大写字母A,B,C等表示.
- 基本事件:由单个样本点组成的单点集.
- 事件发生:在每次试验中,当且仅当事件的结果集合中一个样本点出现时,称这一事件发生.
- 必然事件:在每次试验中总是发生的,称为必然事件,记为S。必然事件包含样本空间S所有样本点,它是样本空间S自身的子集.
- 不可能事件:在任何一次试验中都不发生的事件称为不可能事件,记为∅。不可能事件∅不包含任何样本点,它也是样本空间的子集.
第02回: 事件关系集运算
1.事件间的关系
| 名称 | 符号 | 从事件发生角度理解 | 集合定义 | 图示 |
|---|---|---|---|---|
| A包含B | B⊂A | 事件B发生必有事件A发生 | B是A的子集 | |
| A与B相等 | A=B | 事件A发生必有事件B方法,且事件B发生必有事件A发生 | A与B所包含样本点相同 | |
| A与B的和 | A∪B | 事件A∪B发生<=>事件A发生或事件B发生 | A与B的并集 | |
| A与B的积 | A∩B或AB | 事件A∩B发生<=>事件A发生且事件B发生 | A与B的交集 | |
| A与B的差 | A-B或A-AB或A非B | 事件A-B发生<=>事件A发生且事件B不发生 | 属于A而不属于B的样本点组成的集合 | |
| A与B互斥 | AB=∅ | 事件A与事件B不会同时发生 | A与B没有共同的样本点 | |
| A的对立事件 | 非A | 每次试验事件A与事件feiA有一个发生且仅有一个发生 | A∪ A ‾ \overline{A} A=S,A A ‾ \overline{A} A=∅ | |
2.事件运算的性质
-
交换律:
A∪B=B∪A; A∩B=B∩A.
-
结合律:
A∪(B∪C)=(A∪B)∪C;
A∩(B∩C)=(A∩B)∩C.
-
分配律:
A∪(B∩C)=(A∪B)∩(A∪C);
A∩(B∪C)=(A∩B)∪(A∩C).
-
德摩根律:
A U B ‾ \overline{AUB} AUB= A ‾ \overline{A} A∩ B ‾ \overline{B} B, A ∩ B ‾ \overline{A∩B} A∩B= A ‾ \overline{A} A∪ B ‾ \overline{B} B;
A ∪ B ∪ C ‾ \overline{A∪B∪C} A∪B∪C= A ‾ \overline{A} A∩ B ‾ \overline{B} B∩ C ‾ \overline{C} C, A ∩ B ∩ C ‾ \overline{A∩B∩C} A∩B∩C= A ‾ \overline{A} A∪ B ‾ \overline{B} B∪ C ‾ \overline{C} C
注:德摩根率:长杠变短杠,开口换方向。
第03回:什么是概率
概率是衡量一件事发生的可能性大小的数值!
1.概率的频率定义
在大量重复试验下,随着试验次数的增加,一个事件A出现的频率总在一个固定的数值附近摆动,我们把这个“固定的数”称为事件A的概率。
2.概率的公理化定义
设E是随机试验,S是它的样本空间,对于E的每一个事件A赋予一个实数,记为P(A),称为事件A的概率,如果集合函数P()满足下列条件:
-
非负性:对于每一个事件A,有P(A)≥0;
-
规范性:对于必然事件S,有P(S)=1;
-
可列可加性:设A1,A2…是两两互不相容的事件,即对于
i ≠ j , A i A j = Φ , i , j = 1 , 2 , . . . 则有 i≠j,A_iA_j=Φ,i,j=1,2,... 则有 i=j,AiAj=Φ,i,j=1,2,...则有
3.概率的性质
- P(∅)=0,P(S)=1;
- 有限可加性:设A1,A2…An是两两互不相容的事件,则有
- 逆事件的概率:对于任意事件A,有P(A)=1-P(A);
- 减法公式:设A,B是两个事件,P(A-B)=P(A B ‾ \overline{B} B)=P(A)-P(AB)。特别地,若A⊂B,有P(A)<= P(B),且P(B-A)=P(B)-P(A)
- 加法公式:对于任意两随机事件A,B有: P(AUB)=P(A)+P(B)-P(AB)
注:3个事件的概率加法公式:
P(AUBUC)=P(A)+P(B)+ P©-P(AB)-P(BC)-P(AC)+P(ABC).
第04回:古典概型
1.古典概型(等可能概型)
定义:一个试验的样本点有限,并且每个样本点出现的可能性都相等,那这个试验就是古典概型(等可能概型),比如扔骰子,每个点数出现的可能性都是1/6。
计算方法:
比如A=扔骰子扔出奇数,P(A)=3/6=1/2
2.几何概型
如果试验E是从某一线段(或平面、空间中有界区域)Ω上取一点,并且所取的点位于Ω中任意两个长度(或平面、体积)相等的子区间(或子区域)内的可能性相同,则所取得点位于Ω中的任意子区间(或子区域)A内这一事件(仍记作A)的概率为:
例1:甲乙两人约好上午8点到12点见面,谁先到等对方一小时离去,求甲乙两人能见面的概率。
解:设A={两人能见面} P(A)
甲到的时间为x,乙到的时间为y
A={(x,y)|y-x<=1 或 x-y<=1}
P(A) = (16-9)/(4*4) = 7/16
第05回: 条件概率与乘法法则
1.条件概率的概念
条件概率P(B|A)表示已知事件A发生的情况下事件B发生的概率:
2.条件概率的性质
- 0 <= P(B|A)<=1
- P(S|A)=1
- P( A ‾ \overline{A} A|B)=1-P(A|B)
- P(A+B|C) = P(A|C)+P(B|C)-P(AB|C)
3.乘法法则
第06回:全概率公式与贝叶斯公式
P(A)=P(AB1)+P(AB2)+P(AB3)
注:B1,B2,B3将样本空间占完,即叫做完备事件组。
1.全概率公式
2.贝叶斯公式
注:贝叶斯公式实质就是条件概率公式。
第07回:事件的独立性
1.事件的独立性
设A和B是两件事,若满足P(AB)=P(A)P(B),则称事件A和B相互独立。
2.事件独立性的相关结论
- A和B相互独立<=>P(AB)=P(A)P(B)
<=>P(B)=P(B|A) (P(A)>0)
<=>P(B|A)=P(B| A ‾ \overline{A} A) (0<P(A)<1)
<=>P(A|B)=P(A| B ‾ \overline{B} B) (0<P(B)<1)
注:A发不发生不影响B的结果。
-
A和B相互独立,这A和 B ‾ \overline{B} B, A ‾ \overline{A} A和B, A ‾ \overline{A} A和 B ‾ \overline{B} B也相互独立;
-
当0<P(A)<1,0<P(B)<1时,A和B相互独立与A和B互不相容不能同时成立,也就是独立则不互斥,互斥则不独立,因为A和B互不相容 <=> AB=∅ <=> P(AB)=0
如果A事件是扔骰子扔出奇数,A={1,3,5},B是扔出点数大于4,B={5,6},两者的交集为5并不互斥,但“扔出奇数”事件和“扔出大于4的点数”事件之间是独立的这与P(AB)=P(A)P(B)>0是矛盾的。
-
三个时间A,B,C相互独立,则满足
- P(AB)=P(A)P(B)
- P(BC)=P(B)P©
- P(AC)=P(A)P©
- P(ABC)=P(A)P(B)P©
若只满足前三个式子,则叫做两两相互独立。
互不相容、对立、独立对比:
- 互不相容:AB=∅
- 对立:AB=∅ A∪B=S
- 独立:P(AB)=P(A)P(B)
第08回:离散型随机变量
1. 随机变量
定义:随机变量X是定义在随机试验样本空间S={e}上的单实值函数,记为X=X(e)。
注:
- 随机变量X=X(e)是一个单实值函数,也就是随机试验的每个结果在实数轴上只有一个值与之对应,当然,不同元素对应的实数值可能是一样的,比如年龄问题,很多人都对应 60这个年龄数值;
- X(e)体现的是对随机事件的描述;
- X(e)的各个取值都有一定的概率;
- 试验之前可知X(e)的取值范围,但无法预知取到何值。
2.离散型随机变量
离散型随机变量是指随机变量的全部可能取值是有限个或可列无限个。可列无限个事指能与自然数一一对应上。
离散型随机变量的分布率:
设离散型随机变量X的所有可能取值为xk(k=1,2,…),x取到各个可能值的概率P(X=xk)=pk,(k=1,2,3,…),称为随机变量X的概率分布,也叫分布律。
| X | x1 | x2 | x3 | … | xn | … |
|---|---|---|---|---|---|---|
| Pk | p1 | p2 | p3 | … | pn | … |
注:
- pk>=0,(k=1,2,…)
-
3.常见的离散型随机变量
0-1分布
随机试验的结果只有两个,随机变量X只有两个可能取值0和1,其分布规律可以写成:
| X | 0 | 1 |
|---|---|---|
| Pk | 1-p | p |
比如抛硬币,产品是否合格,一个事件是否发生。
二项分布
只有两个结果的随机试验称为伯努利试验,观察A发生或A不发生,将这种试验独立重复进行n次,称为n重伯努利试验。n重伯努利试验中A发生的次数也是一个随机变量:
假设单独一次试验A发生的概率为p(0<p<1),而A不发生的概率为q(q=1-p),则n次试验中A发生k次的概率为:
我们把这个n重伯努利试验中A发生的次数这个随机变量X服从的分布称为二项分布记为B(n,p).
泊松分布
泊松分布适合于描述单位时间(空间)内随机事件发生的次数。如加油站一小时内到达的车辆数,一个医院一天内出生的新生儿数量,手上单位面积内细菌分布的数量等等。
泊松分布用P(λ),π(λ)表示,其分布律:
这里λ>0是一个常数,表示单位时间(空间)内随机事件发生的平均次数。X~P(λ)表示随机变量X服从参数为λ的泊松分布。
顺口溜:拉ke负拉比上负阶乘
例题:一部热线电话每分钟接到电话的次数服从参数为4的泊松分布,求某一分钟内恰好接到8个电话的概率。
泊松定理
注:泊松定理就是告诉我们,当n特别大的时候,二项分布就可以近似的看成泊松分布了。
例:设某工厂生成零件的次品率是0.1%,且各个零件是否是次品是相互独立的,求1000个零件中至少有2个是次品的概率。
4.随机变量的分布函数
定义:设x是随机变量,x是任意实数,则函数F(x)=P(X<=x),-∞<x<+∞称为X的分布函数。
分布函数表示将随机变量X取值中小于等于x的所有取值对应的概率相加!
注:
- F(x)是一个不减函数
- P(a<x<=b)=F(b)-F(a);
- 0<=F(x)<=1,F(-∞)=0,F(+∞)=1;
- F(x)右连续
第09回:一维连续型随机变量
1.连续型随机变量及其概率密度
定义:如果对于随机变量X的分布函数F(x),存在非负可积函数f(x),使对任意实数x有
则称X为连续型随机变量,f(x)称为X的概率密度函数,简称概率密度。
注:
-
f(x)>=0
-
-
P(x1<X<=x2)=F(x2)-F(x1)=
P(x1<X<=x2)=P(x1<=X<=x2)=P(x1<=X<x2)=P(x1<X<x2);
-
若f(x)在点x处连续,则有F`(x)=f(x)
2.常见的连续型随机变量
均匀分布
若连续型随机变量X具有概率密度
f ( x ) = { 1 b − a , a < x < b 0 , 其他 f(x)=\begin{cases} 1 \over b-a, & a<x<b \\ 0, & 其他 \end{cases} f(x)={b−a,10,a<x<b其他
则称X在区间(a,b)上服从均匀分布,记为X~U(a,b)
X的分布函数为:
F ( x ) = { 0 , x < a x − a b − a a < = x < b 1 x > = b F(x)=\begin{cases} 0, & x<a \\ x-a \over b-a & a<=x<b \\ 1 & x>=b \end{cases} F(x)=⎩ ⎨ ⎧0,b−ax−a1x<aa<=x<bx>=b
指数分布
若连续型随机变量X具有概率密度
f ( x ) = { λ e − λ x , x > 0 0 , 其他 f(x)=\begin{cases} λe^{-λx}, & x>0 \\ 0, & 其他 \end{cases} f(x)={λe−λx,0,x>0其他
其中λ>0为常数,则称X服从参数为λ的指数分布,记为X~E(λ)
X的分布函数为:
f ( x ) = { 1 − e − λ x , x > 0 0 , 其他 f(x)=\begin{cases} 1-e^{-λx}, & x>0 \\ 0, & 其他 \end{cases} f(x)={1−e−λx,0,x>0其他
指数分布的无记忆性:
对于任意的s,t>0,有P(X>s+t | X>s)=P(X>t)
一个元件的寿命服从指数分布,那么它已经工作了s小时,还能继续工作t小时的概率就等于从最开始这个元件能工作t小时的概率。只看时间间隔,不看起始时间。
正态分布
正态分布(Normal distribution),也叫常态分布,高斯分布。
正态分布怎么来的?
注:
-
这个函数的解析式是:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vp94pt5l-1686022186342)(C:\Users\renanquan\AppData\Roaming\Typora\typora-user-images\image-20230530094327077.png)]
-
服从正态分布记作X~N(μ,σ2),读作“X服从正态分布”
-
这里的μ指的就是期望,也就是这组数据的平均数;
这里的σ指的就是标准差,标准差就是方程开根号,
那么σ2就是方差咯,所以它描述的是这组数据的分散程度。
正态分布的性质:
-
曲线在x轴上方,与x轴不相交;
-
曲线是单峰的,它关于直线x =u对称;
-
曲线在x=μ处达到峰值
;
-
曲线与x围成的面积是1;(记住就好了)
-
当σ一定时,曲线的位置由μ确定,随着μ的变化沿着x轴平移;
-
由于曲线与x轴围城的面积是固定的,那么当μ一定时,曲线的形状由σ确定,σ越小(越集中)曲线就高瘦,σ越大(越分散)曲线越矮胖.
3σ原则是什么鬼?
标准正态分布
若X~N(0,1),则称X服从标准正态分布,有概率密度:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Dejl4RDX-1686022186344)(C:\Users\renanquan\AppData\Roaming\Typora\typora-user-images\image-20230530094123215.png)]
注:
-
关于x=0对称,f(-x)=f(x)
-
分布函数Φ(-x)=1-Φ(x);
-
若X~N(μ,σ2),则
此时
-
-
第10回:随机变量函数的分布
1.离散型随机变量函数的分布
例1.已知随机变量X的分布率如下表所示
| X | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| P | 1 12 {1 \over 12} 121 | 1 6 {1 \over 6} 61 | 1 3 {1 \over 3} 31 | 1 12 {1 \over 12} 121 | 2 9 {2 \over 9} 92 | 1 9 {1 \over 9} 91 |
问:求Y=(X-2)2的分布率?
解:
| Y=(X-2)2 | 4 | 1 | 0 | 1 | 4 | 9 |
|---|---|---|---|---|---|---|
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 1 12 {1 \over 12} 121 | 1 6 {1 \over 6} 61 | 1 3 {1 \over 3} 31 | 1 12 {1 \over 12} 121 | 2 9 {2 \over 9} 92 | 1 9 {1 \over 9} 91 |
合并后得
| Y | 0 | 1 | 4 | 9 |
|---|---|---|---|---|
| P | 1 3 {1 \over 3} 31 | 1 4 {1 \over 4} 41 | 11 36 {11 \over 36} 3611 | 1 9 {1 \over 9} 91 |
例2.已知随机变量X的分布函数为
F ( x ) = { 0 x < − 1 1 3 − 1 < = x < 0 1 2 0 < = x < 1 2 3 1 < = x < 2 1 x > = 2 F(x)=\begin{cases} 0 & x<-1 \\1\over3 & -1<=x<0\\1\over2 & 0<=x<1\\2\over3 & 1<=x<2\\1 & x>=2\\ \end{cases} F(x)=⎩ ⎨ ⎧03121321x<−1−1<=x<00<=x<11<=x<2x>=2
求Y=(sin π 6 {π \over6 } 6πX)2的分布函数。
解:
-
X的分布率
X -1 0 1 2 P 1 3 {1 \over 3} 31 1 6 {1 \over 6} 61 1 6 {1 \over 6} 61 1 3 {1 \over 3} 31 -
Y的分布率
Y 1 4 {1 \over 4} 41 0 1 4 {1 \over 4} 41 1 4 {1 \over 4} 41 X -1 0 1 2 P 1 3 {1 \over 3} 31 1 6 {1 \over 6} 61 1 6 {1 \over 6} 61 1 3 {1 \over 3} 31 将其合并即可。
2.连续型随机变量函数的分布
分布函数法:设随机变量X的概率密度函数为[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nrKRjQHD-1686022186345)(C:\Users\renanquan\AppData\Roaming\Typora\typora-user-images\image-20230530102956077.png)]那么Y=g(X)的分布函数为其概率密度函数为[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LnpQOIhc-1686022186345)(C:\Users\renanquan\AppData\Roaming\Typora\typora-user-images\image-20230530103124659.png)]
例1. 设随机变量X的分布函数为F(x),则随机变量Y=2X+1的分布函数G(y)=(F( 1 2 {1 \over 2} 21y- 1 2 {1 \over 2} 21))
解:G(y)=P(Y<=y)=P(2X+1<=y)=P(X<= $ y-1 \over 2$)
由F(x)=P(X<=x)知:
=F( y − 1 2 y-1\over2 2y−1)
=F( y 2 y\over2 2y- 1 2 1\over2 21)
第11回:二维离散型随机变量
1.二维随机变量
定义︰设E是一个随机试验,其样本空间为S={e},设X=X(e),Y=Y(e)是定义在样本空间S={e}上的随机变量,则由它们构成的一个向量(X,Y),叫做二维随机向量,或二维随机变量.
2.二维离散型随机变量
引例:小明同学网购数据
| X\Y | 5 | 6 | 7 | P(X=xi) |
|---|---|---|---|---|
| 10 | 0.05 | 0.15 | 0.20 | 0.4 |
| 12 | 0.07 | 0.11 | 0.22 | 0.4 |
| 15 | 0.04 | 0.07 | 0.09 | 0.2 |
| p(Y=yi) | 0.16 | 0.33 | 0.51 | 1 |
2.1 联合分布率
P{X=xi,Y=yi}=Pij,(i,j=1,2,…)
2.2 联合分布函数
2.3 边缘分布
单独考虑随机变量X或随机变量Y的分布情况:
随机变量X的边缘分布率:
分布函数:
随机变量Y的边缘分布率:
分布函数:
2.4条件分布
例:
2.5独立性
在实际应用中,我们会关心两个随机变量之间是否存在某些依赖关系,还是相互独立的。比如身高和体重,身高高的通常体重也会重,因此身高和体重之间存在一定的线性关系,不是独立的。
对于二维随机离散型随机变量:
随机变量X,Y相互独立<=>Pij=Pi·xP·j,(i,j=1,2,…)
<=>F(x,y)=FX(x)·FY(y)
第12回:二维连续型随机变量
1.联合分布函数
注:
-
-
-
设G是xOy平面上的区域,则点(X,Y)落在G内的概率为
例:
- 若f(x,y)在店(x,y)处连续,则有
2.边缘分布
3.条件分布
4.独立性
对于二维连续随机变量:
随机变量X,Y相互独立<=>f(x,y)=fX(x)·fY(y)
5.常用的二维分布
-
二维均匀分
如果二维随机变量(X,Y)有概率密度 f ( x , y ) = { 1 A ( x , y ) ∈ G , 0 其他 f(x,y)=\begin{cases} 1 \over A & (x,y)∈G,\\ 0 & 其他 \end{cases} f(x,y)={A10(x,y)∈G,其他,其中G为平面有界区域,其面积为A,则称(X,Y)在G上服从二维均匀分布
-
二维正态分布
第13回:二维随机变量函数的分布
1.二维离散型随机变量函数的分布
例1. 设随机变量X,Y的联合分布律为:
| x\Y | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 1/5 | 0 | 1/5 |
| 2 | 1/5 | 1/5 | 1/5 |
求: Z1=X+Y ,Z2=max(X,Y)的分布律.
解:
| Z1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| P | 1/5 | 1/5 | 2/5 | 1/5 |
| Z2 | 1 | 2 | 3 |
|---|---|---|---|
| P | 1/5 | 2/5 | 2/5 |
2.二维连续型随机变量函数的分布
特殊类型:
-
Z=X+Y
-
Z= Y X Y \over X XY,Z= Y X Y \over X XY
-
Z=XY
-
最大值,最小值函数
Z=max(X,Y) 或 Z=min(X,Y)
第14回:期望与方差
1.随机变量的数学期望
在概率论和统计学中,数学期望(mathematic expectation [4] )(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
数学期望:随机变量由概率加权的平均值。
加权平均值:期末成绩=平时成绩*30%+期末卷分数*70%
1.1离散型随机变量的数学期望
1.2连续型随机变量的数学期望
1.3随机变量数学期望的性质
- 设C为常数,则有E©=C;
- 设X为一随机变量,且E(X)存在,C为常数,则有E(CX)=CE(X);
- 设X与Y是两个随机变量,则有E(X±Y)=E(X)±E(Y);
- 设X与Y是两个随机变量,则有E(aX±bY)=aE(X)±bE(Y);
- 设X与Y相互独立,则有E(XY)=E(X)E(Y),(反之不成立)
1.4随机变量函数的数学期望
-
一维随机变量函数的数学期望
-
两个随机变量函数的数学期望
2.随机变量的方差
概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
方差是衡量源数据和期望值相差的度量值。
方差:偏差平方的概率加权平均值。它是用来衡量平均偏离程度(稳定性)
2.1 方差定义
2.2方差的计算公式:平方的期望-期望的平方
2.3方差的性质
-
设C为常数,则D©=0;
-
如果X为随机变量,C为常数,则D(CX)=C2D(X);
-
如果X为随机变量,C为常数,则有D(X+C)=D(X);
-
若X,Y相互独立,则D(X±Y)=D(X)+D(Y)
更一般地:D(aX+bY)=a2D(X)+b2D(Y)
3.常用随机变量的数学期望和方差
| 分布 | 参数 | 分布率或概率密度 | 数学期望 | 方差 |
|---|---|---|---|---|
| 0-1分布(伯努利) | P | P{x=k}pk(1-p)1-k (k=0,1) | p | p(1-p) |
| 二项分布B(n,p)(n重伯努利) | n,p | P{x=k}=Cnkpk(1-p)s-k | p | (n-k)p(1-p) |
| 泊松分布P(λ) | λ | λ | λ | |
| 均匀分布U(a,b) | a<b | |||
| 正态分布N() | μ,σ | μ | ||
| 指数分布e(λ) | λ | f ( x ) = { λ e − λ x , x < 0 0 , 其他 f(x)=\begin{cases}λe^{-λx}, & x<0 \\0, & 其他\end{cases} f(x)={λe−λx,0,x<0其他 |
第15回:协方差与相关系数
1.协方差
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
-
协方差定义
设(X,Y)是二维随机变量,且EX和EY都存在,如果E[(X-EX)(Y-EY)]存在,则称为随机变量X与Y的协方差,记作Cov(X,Y),即Cov(X,Y)=E[(X-EX)(Y-EY)]
-
协方差的计算公式
Cov(X,Y)=E(XY)-E(X)E(Y)
-
协方差的性质:
-
Cov(X,Y)=Cov(Y,X);
-
Cov(X,Y+Z)=Cov(X,Y)+Cov(X,Z);
-
Cov(aX,bY)=abCov(X,Y),其中a,b为任意常数
-
Cov(C,X)=0,其中C为任意常数
-
Cov(aX1±bX2,Y)=aCov(X1,Y)±bCov(X2,Y);
-
如果X与Y相互独立,则Cov(X,Y)=0;
-
D(X±Y)=D(X)+D(Y)±2Cov(X,Y)
D(X±Y)=D(X)+D(Y)(X,Y相互独立)
-
常常被量纲(单位所影响),而相关系数则消除了量纲的影响。
2.相关系数
-
相关系数的定义
-
相关系数的性质
|ρXY|≤1。当ρXY=0时,称X与Y不相关.
-
-1≤ρXY≤1,|ρXY|越大,相关性越强
-
ρ X Y = { > 0 正相关 ( = 1 完全正相关 ) = 0 不相关 < 0 负相关 ( = − 1 完全负相关 ) ρ_{XY}=\begin{cases} {>}0 & 正相关(=1 完全正相关) \\ =0 & 不相关\\ {<0} & 负相关(=-1 完全负相关) \end{cases} ρXY=⎩ ⎨ ⎧>0=0<0正相关(=1完全正相关)不相关负相关(=−1完全负相关)
-
随机变量X与Y不相关的等价说法:当DX≠0,DY≠0时,
ρXY=0<=>Cov(X,Y)=0
<=>E(XY)=E(X)E(Y)
<=>D(X±Y)=DX+DY
-
若随机变量X,Y相互独立则X与Y不相关,但反之不一定.
-
3.二维正态分布
注:
-
二维正态分布的两个边缘分布也是正态分布;
-
E(X)=μ1,D(X)=σ12,E(Y)=μ2,D(Y)=σ22,ρXY=ρ;
-
当ρ=0时,X,Y相互独立,也不相关。
补充:两个相互独立的且服从正态分布的随机变量,它们的线性组合还是服从正态分布。
第16回:大数定律与中心极限定理
1.切比雪夫不等式
设随机变量X,其E(X)=μ,D(X)=σ2都存在,则对任意ε>0均有P{|X-E(X)|≥ε}≤ D ( X ) ε 2 D(X) \over ε^2 ε2D(X)或P{|X-E(X)|<ε}≥1- D ( X ) ε 2 D(X) \over ε^2 ε2D(X)
2.大数定律
依概率收敛定义:设X1,X2,…,Xn,…是一个随机变量序列,a是一个常数,如果对于任意给定的正数ε,有则称随机变量序列X1,X2,…,Xn,…依概率收敛与a,记为Xn—》a.
| 名称 | 大数定律 | 注释 |
|---|---|---|
| 切比雪夫大数定律 | 设随机变量序列X1,X2,…两两不相关,且方差均存在,又存在常数C>0,使D(Xi)≤C(i=1,2,…)则对任意ε>0,有 |
在定理条件下有 |
| 辛钦大数定律 | 设随机变量序列X1,X2,…独立同分布,且数学期望存在,即E(Xi)=μ(i=1,2,…),则对任意ε>0,有 |
在定理条件下,有[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WXiXY9N2-1686022186348)(C:\Users\renanquan\AppData\Roaming\Typora\typora-user-images\image-20230601164306213.png)] |
| 伯努利大数定律 | 设μn是n次独立试验中事件A发生的次数,而p是事件A在每次试验中发生的概率,则对任意ε>0,有 |
事件A发生的频率依概率收敛于事件A的概率,即 |
3.中心极限定理
1.林德伯格-莱维(独立同分布)中心极限定理
设随机变量X1,X2,…,Xn,…相互独立同分布,且期望和方差均存在,即E(Xk)=μ,D(Xk)=σ2>0,(k=1,2,3,…)则随机变量之和的标准化变量
的分布函数Fn(x)对于任意x满足:
告诉我们:
2.棣莫弗-拉普拉斯中心极限定理
设随机变量X1,X2…,Xn,…独立同分布,且服从0-1分布,即P(Xk=1)= p,P(Xk =0)=1-p,(0<p<1,k=1,2,3,…),则对于任意x满足:
告诉我们:当n充分大时,
也就是说,当n充分大的时候,二项分布的极限分布是正态分布
补充:独立同分布
独立
独立可以理解为"互不影响".
例如,假若随机变量X1和X2是相互独立的,那么就意味着
- 当X1和X2两个这随机变量的事件相遇时,它们各自的概率没有因此发生变化。
- X1的取值不影响X2的取值
- X2的取值不影响X1的取值.
- P(XY)=P(X)P(Y)
- E(XY)= E(X)E(Y)
- D(X+Y)=D(X)+D(Y)
同分布
同分布可以理解为"服从相同的概率分布".
例如,假若随机变量X1和X2是同分布的,那么就意味着文章来源:https://www.toymoban.com/news/detail-776479.html
- X和X,具有相同的分布形状和相同的分布参数
- 若X1和X2是离散型随机变量,则它们具有相同的分布律
- 若X1和X2是连续型随机变量,则它们具有相同的概率密度函数
- X1和X2有着相同的分布函数,相同的期望、方差
独立同分布
指"服从相同的概率分布并且互相独立”(也就是同时满足了上面提到的两个条件)文章来源地址https://www.toymoban.com/news/detail-776479.html
到了这里,关于概率论学习笔记全网最全!!!!的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!