B3610 [图论与代数结构 801] 无向图的块题解-Toy模板网

这篇具有很好参考价值的文章主要介绍了B3610 [图论与代数结构 801] 无向图的块题解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

B3610 [图论与代数结构 801] 无向图的块题解

$2023$ ，再见。 $2024$ ，你好！

解法

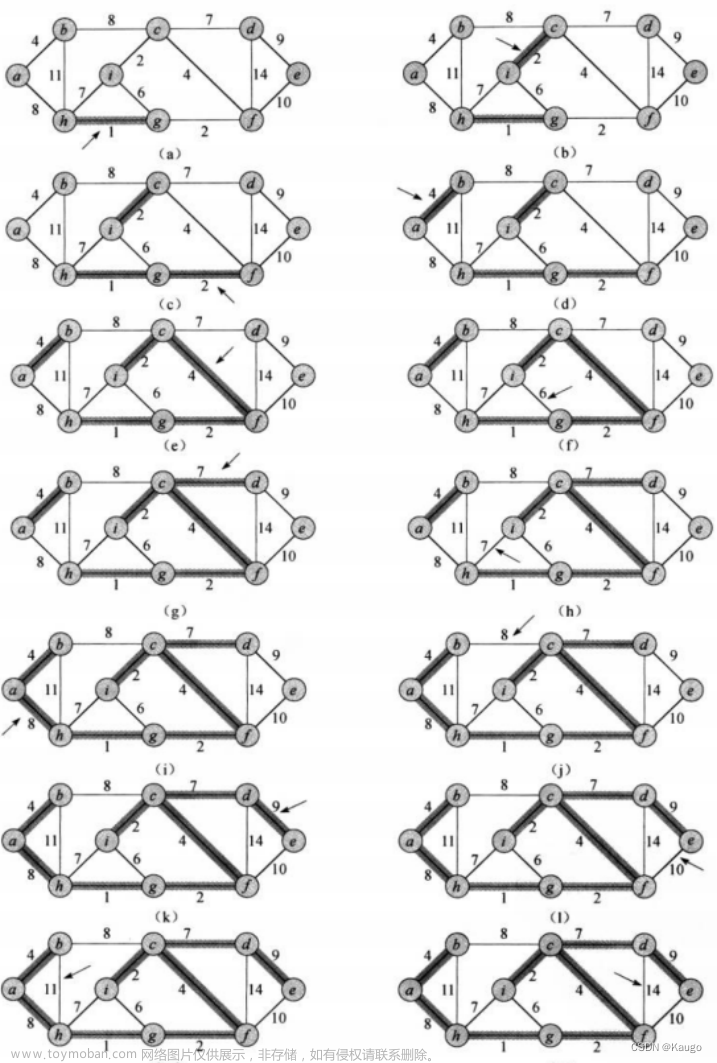
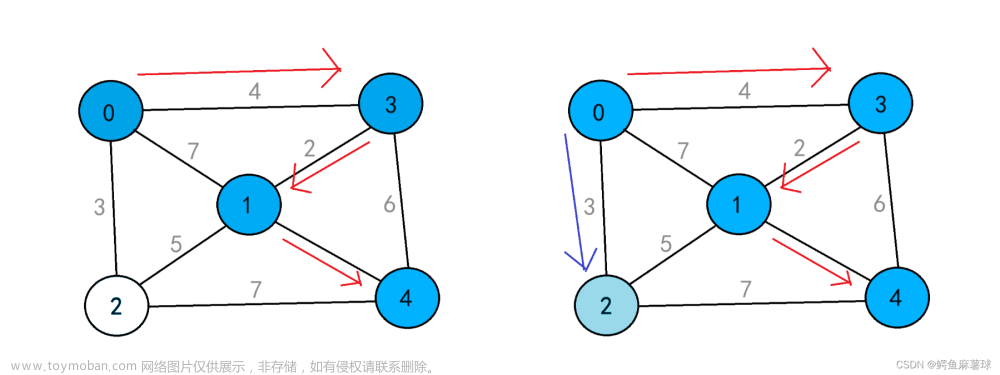
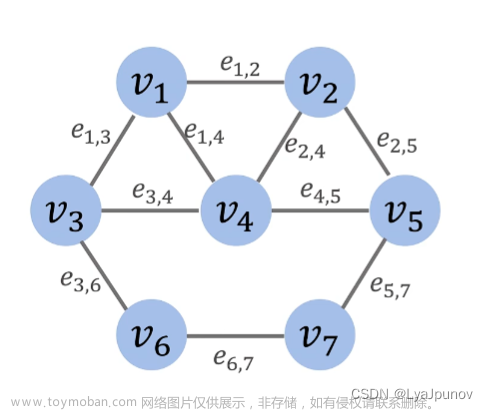
其实就是统计点双连通分量的个数。需要注意的是，孤立点在这里不被看作块。本文使用 tarjan 算法来解决这道题。

概念明晰

时间戳：这里记为 $dfn_i$ ，表示第一次深度优先搜索到节点 $i$ 的时间。时间 $\in \mathbb{N}^+$ 且随这搜索依次递增。
搜索树：从选定的节点出发的深搜，每个节点仅搜索一次，把所有搜索路径组成一颗树，称为搜索树。如果给定的图不是一整个连通图，则称为搜索森林。
追溯值：这里记为 $low_i$ ，表示节点 $i$ 最多经过一条返祖边能走到搜索树中以 $i$ 的子树中的节点的最小 $df n$ 为多少（简洁的定义出自东灯的博客）。
割点：对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点。

追溯值的计算

首先根据定义， $low_i$ 的初始值应赋为 $dfn_i$ 。现在考虑怎么进一步更新 $low_i$ 。

如果在搜索树上 $i$ 是 $j$ 的父节点，则 $low_i = \min(low_i,low_j)$ 。
如果从 $i$ 到 $j$ 的连边不是搜索树上的边，则 $low_i= \min(low_i,dfn_j)$ 。

割点的判定方法

定义搜索树中节点 $i$ 的子树为 $son_i$ 。

如果 $i$ 不是搜索树的根，则当 $\exists dfn_i \le low_j,j \in son_i$ 时， $i$ 是割点。
如果 $i$ 是搜索树的根，则当有两个不同的 $j$ 满足上述条件时， $i$ 是割点。

判定方法的证明

如果 $dfn_i \le low_j$ ，则证明从 $\in son_i$ 出发，不经过点 $i$ 无论如何也不能到达 $i$ 的祖先。所以如果把 $i$ 删去，则 $son_i$ 就会与原图分离。文章来源地址https://www.toymoban.com/news/detail-776607.html

代码

#include<bits/stdc++.h>
using namespace std;
#define Getchar() p1==p2 and (p2=(p1=Inf)+fread(Inf,1,1<<7,stdin),p1==p2)?EOF:*p1++
#define Putchar(c) p3==p4 and (fwrite(Ouf,1,1<<7,stdout),p3=Ouf),*p3++=c
char Inf[1<<7],Ouf[1<<7],*p1,*p2,*p3=Ouf,*p4=Ouf+(1<<7);
inline void read(int &x,char c=Getchar())
{
	bool f=c!='-';
	x=0;
	while(c<48 or c>57) c=Getchar(),f&=c!='-';
	while(c>=48 and c<=57) x=(x<<3)+(x<<1)+(c^48),c=Getchar();
	x=f?x:-x;
}
inline void write(int x)
{
	if(x<0) Putchar('-'),x=-x;
	if(x>=10) write(x/10),x%=10;
	Putchar(x^48);
}
struct my_stack
{
	int top,a[500010];
	inline int size()
	{
		return top;
	}
	inline int &operator[](const int &x)
	{
		return a[x];
	}
	inline int back()
	{
		return a[top];
	}
	inline void push_back(const int &x)
	{
		a[++top]=x;
	}
	inline void pop_back()
	{
		top--;
	}
	inline void clear()
	{
		top=0;
	}
};
my_stack v;
int n,m,head[500010],cnt,dfn[500010],low[500010],times,belong[500010],tot;
vector<int> ans[500010];
struct edge
{
	int to,next;
};
edge e[4000010];
inline void add(const int &x,const int &y) noexcept
{
	e[++cnt].to=y,e[cnt].next=head[x],head[x]=cnt;
}
inline void tarjan(const int &pos,const int &fa)
{
	int son=0;
	dfn[pos]=low[pos]=++times,v.push_back(pos);
	for(int i=head[pos];i;i=e[i].next)
		if(!dfn[e[i].to])
		{
			son++,tarjan(e[i].to,pos),low[pos]=min(low[pos],low[e[i].to]);
			if(low[e[i].to]>=dfn[pos])
			{
				tot++;
				while(v[v.top+1]!=e[i].to) ans[tot].push_back(v.back()),v.pop_back();
				ans[tot].push_back(pos);
			}
		}else if(e[i].to!=fa) low[pos]=min(low[pos],dfn[e[i].to]);
}
int main()
{
	read(n),read(m);
	for(int i=1,x,y;i<=m;i++) read(x),read(y),add(x,y),add(y,x);
	for(int i=1;i<=n;i++) if(!dfn[i]) v.clear(),tarjan(i,0);
	for(int i=1;i<=tot;i++) std::sort(ans[i].begin(),ans[i].end());
	std::sort(ans+1,ans+tot+1,[](std::vector<int> &lhs,std::vector<int> &rhs)
	{
		for(int i=0;i<std::min(lhs.size(),rhs.size());i++) if(lhs[i]!=rhs[i]) return lhs[i]<rhs[i];
		return lhs.size()<rhs.size();
	});
	write(tot),Putchar('\n');
	for(int i=1;i<=tot;i++,Putchar('\n'))
	{
		for(int j=0;j<ans[i].size();j++) write(ans[i][j]),Putchar(' ');
	}
	fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
	return 0;
}