⛄一、遗传算法及栅格地图简介
1 遗传算法
遗传算法是一种基于生物进化论模型的优化算法,通过模拟生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。遗传算法可以用于解决各种优化问题,如函数优化、组合优化、机器学习等。在遗传算法中,个体的适应度函数值越高,就越有可能被选择为下一代的父代,从而进化出更优秀的解。遗传算法的优点是可以在大规模搜索空间中找到全局最优解,但是也存在一些缺点,如收敛速度慢、参数设置困难等。
2 遗传算法步骤
遗传算法是一种模拟自然进化过程的优化算法,其步骤如下:
(1)初始化种群:随机生成一定数量的个体,每个个体都是由若干个基因组成的染色体。
(2)评估适应度:对于每个个体,通过一个适应度函数来评估其适应度,即该个体在解决问题中的表现好坏。
(3)选择操作:根据适应度函数的值,选择一部分个体作为父代,用于产生下一代个体。
(4)交叉操作:对于选出的父代个体,进行交叉操作,生成新的个体。
(5)变异操作:对于新生成的个体,进行变异操作,引入新的基因,增加种群的多样性。
(6)重复步骤2-5,直到达到预设的终止条件(如达到最大迭代次数或找到满足要求的解)。
3 遗传算法求解带容量和体积的车辆路径规划问题
遗传算法是一种基于生物进化原理的优化算法,可以用于求解带容量和体积的车辆路径规划问题。具体实现过程如下:
(1)定义染色体编码方式,将车辆路径规划问题转化为染色体的编码问题。
(2)初始化种群,随机生成一定数量的染色体。
(3)评估适应度,根据染色体编码计算每个染色体的适应度。
(4)选择操作,根据适应度选择一定数量的染色体作为下一代的父代。
(5)交叉操作,对父代染色体进行交叉操作,生成新的染色体。
(6)变异操作,对新生成的染色体进行变异操作,增加种群的多样性。
(7)评估适应度,计算新生成的染色体的适应度。
(8)选择操作,根据适应度选择一定数量的染色体作为下一代的种群。
(9)重复步骤4-8,直到满足停止条件。
在带容量和体积的车辆路径规划问题中,染色体编码可以采用基因串编码,其中每个基因表示一个客户点,基因串表示车辆的路径。同时,需要引入容量和体积约束条件,确保每个车辆的容量和体积不超过限制。在评估适应度时,可以考虑车辆的行驶距离和满足约束条件的程度。
2 栅格地图
2.1 栅格法应用背景
路径规划时首先要获取环境信息, 建立环境地图, 合理的环境表示有利于建立规划方法和选择合适的搜索算法,最终实现较少的时间开销而规划出较为满意的路径。一般使用栅格法在静态环境下建立环境地图。
2.2 栅格法实质
将AGV的工作环境进行单元分割, 将其用大小相等的方块表示出来,这样栅格大小的选取是影响规划算法性能的一个很重要的因素。栅格较小的话,由栅格地图所表示的环境信息将会非常清晰,但由于需要存储较多的信息,会增大存储开销,同时干扰信号也会随之增加,规划速度会相应降低,实时性得不到保证;反之,由于信息存储量少,抗干扰能力有所增强,规划速随之增快,但环境信息划分会变得较为模糊,不利于有效路径的规划。在描述环境信息时障碍物所在区域在栅格地图中呈现为黑色,地图矩阵中标为1,可自由通行区域在栅格地图中呈现为白色,地图矩阵中标为0。路径规划的目的就是在建立好的环境地图中找到一条最优的可通行路径,所以使用栅格法建立环境地图时,栅格大小的合理设定非常关键。
2.3 10乘10的静态环境地图
10乘10的静态环境地图代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%建立环境地图%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function DrawMap(map)
n = size(map);
step = 1;
a = 0 : step :n(1);
b = 0 : step :n(2);
figure(1)
axis([0 n(2) 0 n(1)]); %设置地图横纵尺寸
set(gca,'xtick',b,'ytick',a,'GridLineStyle','-',...
'xGrid','on','yGrid','on');
hold on
r = 1;
for(i=1:n(1)) %设置障碍物的左下角点的x,y坐标
for(j=1:n(2))
if(map(i,j)==1)
p(r,1)=j-1;
p(r,2)=i-1;
fill([p(r,1) p(r,1) + step p(r,1) + step p(r,1)],...
[p(r,2) p(r,2) p(r,2) + step p(r,2) + step ],'k');
r=r+1;
hold on
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%栅格数字标识%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x_text = 1:1:n(1)*n(2); %产生所需数值.
for i = 1:1:n(1)*n(2)
[row,col] = ind2sub([n(2),n(1)],i);
text(row-0.9,col-0.5,num2str(x_text(i)),'FontSize',8,'Color','0.7 0.7 0.7');
end
hold on
axis square
建立环境矩阵,1代表黑色栅格,0代表白色栅格,调用以上程序,即可得到上述环境地图。
map=[0 0 0 1 0 0 1 0 0 0;
1 0 0 0 0 1 1 0 0 0;
0 0 1 0 0 0 1 1 0 0;
0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 1 0 0 1 0;
1 0 0 0 0 1 1 0 0 0;
0 0 0 1 0 0 0 0 0 0;
1 1 1 0 0 0 1 0 0 0;
0 0 0 0 0 1 1 0 0 0;
0 0 0 0 0 1 1 0 0 0;];
DrawMap(map); %得到环境地图
2.4 栅格地图中障碍栅格处路径约束
移动体栅格环境中多采用八方向的移动方式,此移动方式在完全可通行区域不存在运行安全问题,当
移动体周围存在障碍栅格时此移动方式可能会发生与障碍物栅格的碰撞问题,为解决此问题加入约束
条件,当在分别与障碍物栅格水平方向和垂直方向的可行栅格两栅格之间通行时,禁止移动体采用对
角式移动方式。

约束条件的加入,实质是改变栅格地图的邻接矩阵,将障碍栅格(数字为“1”的矩阵元素)的对角栅格
设为不可达, 即将对角栅格的距离值改为无穷大。其实现MATLAB代码如下:
代码:
%约束移动体在障碍栅格对角运动
%通过优化邻接矩阵实现
%%%%%%%%%%%%%%%%%% 约束移动体移动方式 %%%%%%%%%%%%%%%%%
function W=OPW(map,W)
% map 地图矩阵 % W 邻接矩阵
n = size(map);
num = n(1)*n(2);
for(j=1:n(1))
for(z=1:n(2))
if(map(j,z)==1)
if(j==1) %若障碍物在第一行
if(z==1) %若障碍物为第一行的第一个
W(j+1,j+n(2)*j)=Inf;
W(j+n(2)*j,j+1)=Inf;
else
if(z==n(2)) %若障碍物为第一行的最后一个
W(n(2)-1,n(2)+n(1)*j)=Inf;
W(n(2)+n(1)*j,n(2)-1)=Inf;
else %若障碍物为第一行的其他
W(z-1,z+j*n(2))=Inf;
W(z+j*n(2),z-1)=Inf;
W(z+1,z+j*n(2))=Inf;
W(z+j*n(2),z+1)=Inf;
end
end
end
if(j==n(1)) %若障碍物在最后一行
if(z==1) %若障碍物为最后一行的第一个
W(z+n(2)*(j-2),z+n(2)*(j-1)+1)=Inf;
W(z+n(2)*(j-1)+1,z+n(2)*(j-2))=Inf;
else
if(z==n(2)) %若障碍物为最后一行的最后一个
W(n(1)*n(2)-1,(n(1)-1)*n(2))=Inf;
W((n(1)-1)*n(2),n(1)*n(2)-1)=Inf;
else %若障碍物为最后一行的其他
W((j-2)*n(2)+z,(j-1)*n(2)+z-1)=Inf;
W((j-1)*n(2)+z-1,(j-2)*n(2)+z)=Inf;
W((j-2)*n(2)+z,(j-1)*n(2)+z+1)=Inf;
W((j-1)*n(2)+z+1,(j-2)*n(2)+z)=Inf;
end
end
end
if(z==1)
if(j~=1&&j~=n(1)) %若障碍物在第一列非边缘位置
W(z+(j-2)*n(2),z+1+(j-1)*n(2))=Inf;
W(z+1+(j-1)*n(2),z+(j-2)*n(2))=Inf;
W(z+1+(j-1)*n(2),z+j*n(2))=Inf;
W(z+j*n(2),z+1+(j-1)*n(2))=Inf;
end
end
if(z==n(2))
if(j~=1&&j~=n(1)) %若障碍物在最后一列非边缘位置
W((j+1)*n(2),j*n(2)-1)=Inf;
W(j*n(2)-1,(j+1)*n(2))=Inf;
W(j*n(2)-1,(j-1)*n(2))=Inf;
W((j-1)*n(2),j*n(2)-1)=Inf;
end
end
if(j~=1&&j~=n(1)&&z~=1&&z~=n(2)) %若障碍物在非边缘位置
W(z+(j-1)*n(2)-1,z+j*n(2))=Inf;
W(z+j*n(2),z+(j-1)*n(2)-1)=Inf;
W(z+j*n(2),z+(j-1)*n(2)+1)=Inf;
W(z+(j-1)*n(2)+1,z+j*n(2))=Inf;
W(z+(j-1)*n(2)-1,z+(j-2)*n(2))=Inf;
W(z+(j-2)*n(2),z+(j-1)*n(2)-1)=Inf;
W(z+(j-2)*n(2),z+(j-1)*n(2)+1)=Inf;
W(z+(j-1)*n(2)+1,z+(j-2)*n(2))=Inf;
end
end
end
end
end
2.5 栅格法案例
下面以Djkstra算法为例, 其实现如下:
map=[0 0 0 1 0 0 1 0 0 0;
1 0 0 0 0 1 1 0 0 0;
0 0 1 0 0 0 1 1 0 0;
0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 1 0 0 1 0;
1 0 0 0 0 1 1 0 0 0;
0 0 0 1 0 0 0 0 0 0;
1 1 1 0 0 0 1 0 0 0;
0 0 0 0 0 1 1 0 0 0;
0 0 0 0 0 1 1 0 0 0;];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%建立环境矩阵map%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
DrawMap(map); %得到环境地图
W=G2D(map); %得到环境地图的邻接矩阵
W(W==0)=Inf; %邻接矩阵数值处理
W=OPW(map,W); %优化邻接矩阵
[distance,path]=dijkstra(W,1,100);%设置起始栅格,得到最短路径距离以及栅格路径
[x,y]=Get_xy(distance,path,map); %得到栅格相应的x,y坐标
Plot(distance,x,y); %画出路径
运行结果如下:
其中函数程序:
DrawMap(map) 详见建立栅格地图
W=G2D(map) ; 详见建立邻接矩阵
[distance, path] =dijkstra(W, 1, 100) 详见Djk stra算法
[x, y] =Get_xy(distance, path, map) ;
Plot(distance, x, y) ;
⛄二、部分源代码
% 基于遗传算法的栅格法机器人路径规划
clc;
clear;
close all
tic
%testtttttttttttttttt!
% 输入数据,即栅格地图.20行20列
% Grid= [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
% 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
% 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 0 0;
% 0 1 1 1 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0;
% 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0;
% 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0;
% 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;
% 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0;
% 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0;
% 0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0;
% 0 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0;
% 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0;
% 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0;
% 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
Grid = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0;
0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0;
0 0 1 1 1 0 0 0 0 1 1 0 0 1 0 0 1 1 0 0;
0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0;
0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0;
0 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 1 1 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1;
0 0 1 1 1 1 1 1 1 1 0 0 1 1 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0;
0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0;
0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0;
0 0 0 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0;
0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 1 1 1 0 0 0 1 0 0 1 0 0 0 1 1 1 0 0;
0 0 0 0 1 0 1 0 1 0 0 1 0 0 0 1 1 1 0 0;
0 0 1 1 1 0 1 0 1 1 1 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0];
start_num = 0; % 起点编号
end_num = 399; % 终点序号
NP = 200; % 种群数量
max_gen = 50; % 最大进化代数
% pc = 0.8; % 交叉概率
% pm = 0.2; % 变异概率
r = 8000; %适应度系数
a = 2; % 路径长度比重
b = 5; % 路径顺滑度比重
z = 1;
pc_max=0.8;
pc_min=0.08;
pm_max=0.2;
pm_min=0.02;
new_pop1 = {}; % 元胞数组,存放路径
[y, x] = size(Grid);
% 起点所在列(从左到右编号1.2.3…)
start_column = mod(start_num, x) + 1;
% 起点所在行(从上到下编号行1.2.3…)
start_row = fix(start_num / x) + 1; %Y = fix(X) 将 X 的每个元素朝零方向四舍五入为最近的整数
% 终点所在列、行
end_column = mod(end_num, x) + 1;
end_row = fix(end_num / x) + 1;
%% 种群初始化step1,必经节点,从起始点所在行开始往上,在每行中挑选一个自由栅格,构成必经节点
pass_num = end_row - start_row + 1; %每条路径的节点个数
pop = zeros(NP, pass_num);%生成种群数量*节点个数的矩阵,用于存放每个个体的路径
for i = 1 : NP %每个个体(每行)循环操作:
able_to_continuous = 0;
while able_to_continuous == 0 %检验是否可以连续,如果不连续则重新随机生成路径
pop(i, 1) = start_num; %每行第一列都为起点(存入起点的编号)
j = 1;
% 此for循环用于寻找除去起点和终点所在行以外每行中的自由栅格
for row_i = start_row+1 : end_row-1 %栅格的第二行到倒数第二行循环
j = j + 1;
% 存放栅格里当前行中的自由栅格序号
free = [];
for column_i = 1 : x %从第一列到第二十列中
% 栅格对应的序号
num = (column_i - 1) + (row_i - 1) * x;
% 如果该栅格为非障碍物
if Grid(row_i, column_i) == 0
% 把此栅格的编号加入free矩阵中
free = [free num];
end
end % 栅格一行里的自由栅格查询结束,自由栅格的编号存在了向量中
free_num = length(free);
% 产生小于等于本行自由栅格数量的一个随机整数
index = randi(free_num); %X = randi(imax) 返回一个介于 1 和 imax 之间的伪随机整数标量。
% 将栅格中当前行的自由栅格矩阵free中第index个栅格编号作为当前种群的第j个节点
pop(i, j) = free(index);
end %该个体的每一行的路径节点产生完成,存入了pop的第i行中
pop(i, end) = end_num; %pop的每行第最后一列都为终点(存入终点的编号)
%% 种群初始化step2将上述必经节点联结成无间断路径
single_new_pop = generate_continuous_path(pop(i, :), Grid, x);
if ~isempty(single_new_pop)%如果这一行种群的路径不是空的,将这行路径存入元胞数组中。
new_pop1(z, 1) = {single_new_pop};
z = z + 1;
able_to_continuous=1;
else
able_to_continuous=0;
end
end
end
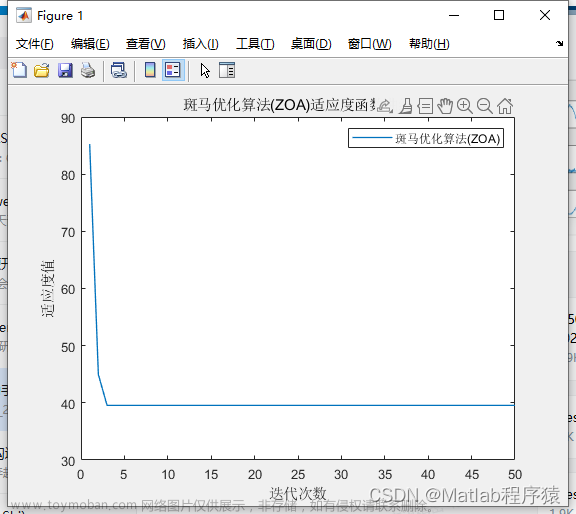
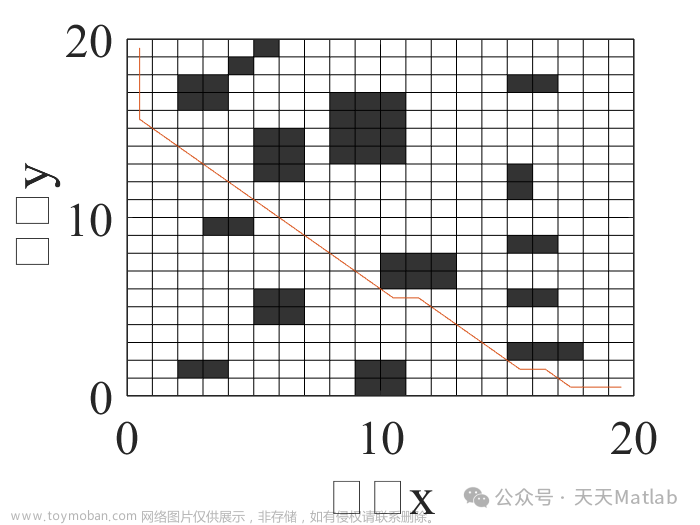
⛄三、运行结果


⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]徐美清,孙晨亮.基于栅格地图的遗传算法路径规划[J].科技信息. 2011,(31)文章来源:https://www.toymoban.com/news/detail-777273.html
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除文章来源地址https://www.toymoban.com/news/detail-777273.html
到了这里,关于【路径规划】自适应遗传算法机器人栅格地图最短路径规划【含Matlab源码 3570期】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!