同态加密详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了同态加密详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

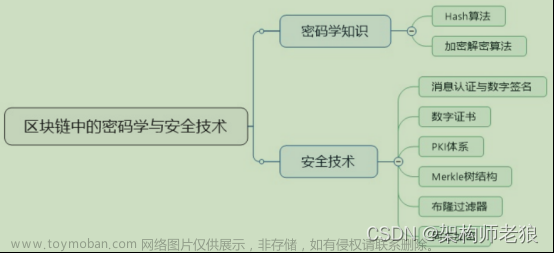
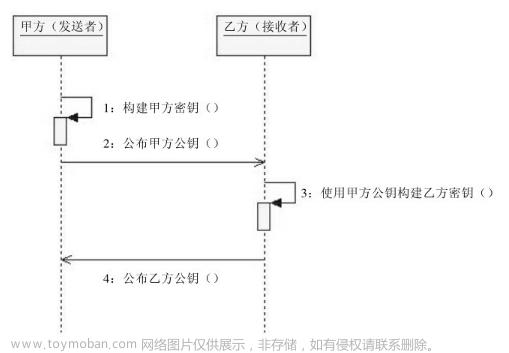
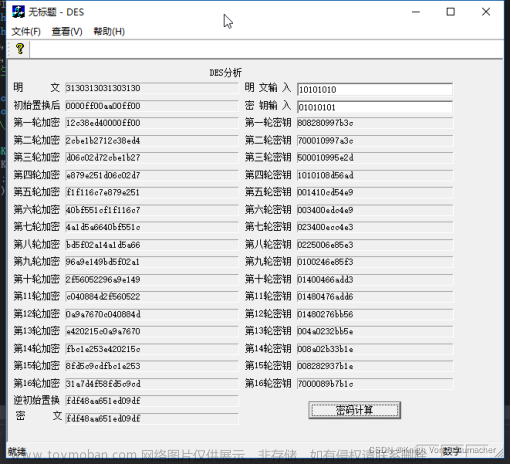
什么是同态加密

同态加密（Homomorphic Encryption）是指将原始数据经过同态加密后，对得到的密文进行特定的运算，然后将计算结果再进行同态解密后得到的明文等价于原始明文数据直接进行相同计算所得到的数据结果。
同态加密与一般加密方案的关注点不同，一般的加密方案关注的是数据存储安全，即我要给其他人发送信息或者存储信息，我需要对数据进行加密之后再发送和存储，这里我们只需要保证在数据传送和存储的过程中不被其他人窃听到即可，在这个过程中用户时不能对加密的结果做任何操作的，否则可能会导致解密失败
通态加密的关注点则是数据处理安全，同态加密提供了一种对加密数据进行处理的功能。也就是说其他人可以对加密后的数据进行处理，在这个过程中不会泄露任何原始的内容，在数据处理完成之后再进行解密，得到的正是对原始数据进行相同处理后的结果。

举个例子（内容来自知乎）
有个叫Alice的用户买到了一大块金子，她想让工人把这块金子打造成一个项链。但是工人在打造的过程中有可能会偷金子啊，毕竟就是一克金子也值很多钱的说… 因此能不能有一种方法，让工人可以对金块进行加工（delegate processing of your data），但是不能得到任何金子（without giving away access to it）？当然有办法啦。Alice可以这么做：

Alice将金子锁在一个密闭的盒子里面，这个盒子安装了一个手套。工人可以带着这个手套，对盒子内部的金子进行处理。但是盒子是锁着的，所以工人不仅拿不到金块，连处理过程中掉下的任何金子都拿不到。加工完成后。Alice拿回这个盒子，把锁打开，就得到了金子。这个盒子的样子大概是这样的：
同态加密,密码学,同态加密,区块链,算法,安全
这里面的对应关系是：

盒子：加密算法
盒子上的锁：用户密钥
将金块放在盒子里面并且用锁锁上：将数据用同态加密方案进行加密
加工：应用同态特性，在无法取得数据的条件下直接对加密结果进行处理
开锁：对结果进行解密，直接得到处理后的结果

加密步骤

本部分内容参考链接

（本地）生成一对公私钥，公钥pub和密钥priv，公钥用于加密，密钥用于解密；
（本地）使用公钥pub分别加密m₁和m₂，得到E_pub(m₁)和E_pub(m₂)；
（第三方）使用Add_pub函数处理E_pub(m₁)和E_pub(m₂)，即Add_pub(E_pub(m₁),E_pub(m₂))；
（本地）使用密钥priv解密Add_pub(E_pub(m₁),E_pub(m₂))，即D_priv(Add_pub(E_pub(m₁),E_pub(m₂)))；

D_priv(Add_pub(E_pub(m₁),E_pub(m₂)))就等于m₁+m₂。第三方通过上述步骤3实现了m₁和m₂在加密状态下做加法的操作。

同态加密的类型

部分同态加密（partially homomorphic）

部分同态加密算法允许某一操作被执行无限次。例如，一个特定的算法可能是加法同态的，这意味着将两个密文相加会产生与加密两个明文之和相同的结果。

加法同态：该加密方案支持的同态函数族为所有可以仅由加法实现的函数。目前使用比较广泛的是paillier加法同态。
乘法同态：该加密方案支持的同态函数族为所有可以仅由乘法实现的函数。比如经典的RSA加密方案。

稍微同态加密（somewhat homomorphic）

有点同态加密算法可以对密文进行有限次数的任意操作，例如，某种程度的同态加密算法可以支持最多五种加法或乘法的任意组合。但是，任何一种类型的第六次操作都将产生无效的结果。

某种同态加密算法是实现完全同态加密的重要垫脚石。设计一个同时支持加法和乘法的算法（即使是支持一组数量的操作）的算法比创建一个允许无限加法或乘法密文的算法要困难的多。

全同态加密（fully homomorphic）

可以对密文进行无限次数的任意同态操作，也就是说它可以同态计算任意的函数

应用场景

参考链接一；参考链接二

云计算

在云计算或外包计算中，用户为了节约自身的软硬件成本，可将计算和存储需求外包给云服务提供商，利用云服务提供商强大的算力资源实现数据的托管存储和处理。但是，将明文数据直接交给云服务器具有一定的安全风险，而传统的加密存储方式则无法实现对密文数据的直接计算，因此如何同时实现数据的机密性和可计算性成为了一个难题，同态加密的出现为这一场景的实现提供了可能性。
在传统的云存储与计算解决方案中，用户需要信任云服务器提供商不会窃取甚至用户数据，而基于同态加密的云计算模型可在根本上解决这一矛盾。首先，用户使用同态加密算法和加密密钥对数据进行加密，并将密文发送给云服务器；云服务器在无法获知明文数据的情况下按照用户给定的程序对密文进行计算，并将密文计算结果返回给用户；用户使用同态加密算法和解密密钥对密文计算结果进行解密，所得结果与直接对明文进行相同计算的结果等价。

具体过程图解：
同态加密,密码学,同态加密,区块链,算法,安全

Alice对数据进行加密。并把加密后的数据发送给Cloud；
Alice向Cloud提交数据的处理方法，这里用函数f来表示；
Cloud在函数f下对数据进行处理，并且将处理后的结果发送给Alice；
Alice对数据进行解密，得到结果。

不足

目前，全同态加密算法的现有方案均存在计算和存储开销大等问题，距离高效的工程应用还有着不小的差距，同时还面临国际与国内相关标准的缺失，因此在半同态加密算法满足需求的情况下要优先使用半同态加密算法。文章来源地址https://www.toymoban.com/news/detail-777322.html

到了这里，关于同态加密详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！