What is a Logit?
A Logit function, also known as the log-odds function, is a function that represents probability values from 0 to 1, and negative infinity to infinity. The function is an inverse to the sigmoid function that limits values between 0 and 1 across the Y-axis, rather than the X-axis. Because the Logit function exists within the domain of 0 to 1, the function is most commonly used in understanding probabilities.

How does a Logit function work?
The Logit function is represented as:
If X represents a probability, then X(1-X) is the odds(概率), and the Logit function is the logarithm of the odds. The function plots across the graph within the domain of 0 to 1, and producing real numbers ranging from negative infinity to infinity.
Logit Functions and Machine Learning
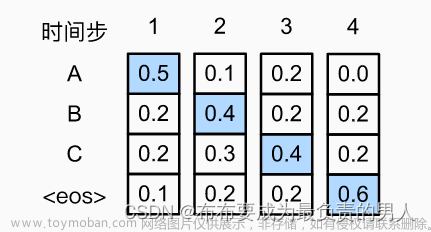
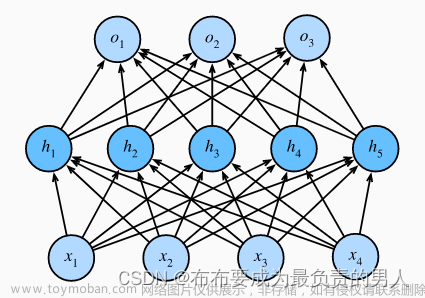
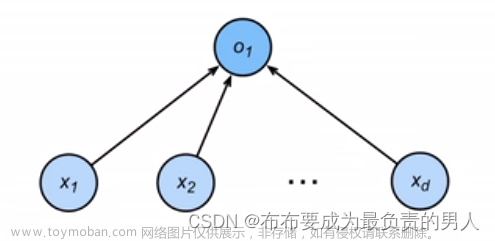
(1)The Logit function is used similarly to the sigmoid function in neural networks. (2)The sigmoid, or activation, function produces a probability, whereas the Logit function takes a probability and produces a real number between negative and positive infinity.(3)Like the sigmoid function, Logit functions are often placed as the last layer in a neural network as can simplify the data. (4)For example, a Logit function is often used in the final layer of a neural network used in classification tasks. (5)As the network determines probabilities for classification, the Logit function can transform those probabilities to real numbers.
原文
https://deepai.org/machine-learning-glossary-and-terms/logit文章来源:https://www.toymoban.com/news/detail-777762.html
“logits”到底是个什么意思?
1. 什么是logits?
说到Logits,首先要弄明白什么是Odds?
在英文里,Odds的本意是指几率、可能性。它和我们常说的概率又有什么区别呢?
在统计学里,概率(Probability)描述的是某事件A出现的次数与所有事件出现的次数之比:
P(A) = 发生事件A的次数 / 所有事件的次数。 (公式1)
很显然,概率 P是一个介于0到1之间的实数; P=0,表示事件A一定不会发生,而P=1,则表示事件A一定会发生。
以掷骰子为例,由于骰子为6面,任意一面上点数概率都是相同。所以,事件A:掷出点数为1的概率为:P=1/6
对比而言,Odds指的是事件发生的概率与事件不发生的概率之比:
Odds(A)= 发生事件A的概率 / 不发生事件A的概率 (公式2)
还拿掷骰子的例子说事,掷出点数为1的Odds为:
很明显,Odds和概率之间的关系为:
进一步简化可知,
Odds(A)= 发生事件A次数 / 其他事件的次数(即不发生A的次数) (公式3)
换句话说,事件A的Odds 等于 事件A出现的次数 和 其它(非A)事件出现的次数 之比;
相比之下,事件A的概率 等于 事件A出现的次数 与 所有事件的次数 之比。
很容易推导得知:
概率P(A)和Odds(A)的值域是不同的。前者被锁定在[0,1]之间,而后者则是(?).
这说了半天,有何logit有什么关系呢?
请注意Logit一词的分解,对它(it)Log(取对数),这里“it”就是Odds。下面我们就可以给出Logit的定义了:
公式4实际上就是所谓Logit变换。
原文:https://blog.csdn.net/nbxzkok/article/details/84838984文章来源地址https://www.toymoban.com/news/detail-777762.html
到了这里,关于Logits——(待完善)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!