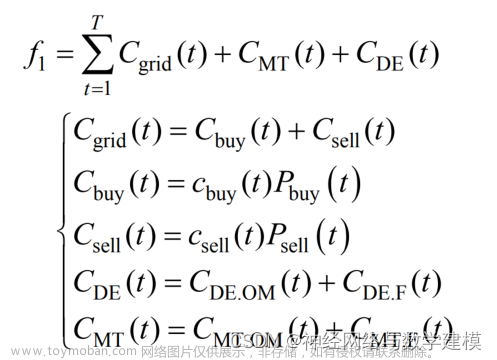鲜奶配送站点的最优化设置问题 - MATLAB 实现
问题描述:
鲜奶配送站点的最优化设置问题是一个经典的运筹学问题,它涉及确定最佳的鲜奶配送站点位置,以最小化总体运输成本。本文将使用 MATLAB 编程来解决这个问题,并提供相应的源代码。
解决方法:
为了解决鲜奶配送站点的最优化设置问题,我们将采用以下步骤:
-
数据收集:收集相关的数据,包括需求点的位置和需求量,以及候选站点的位置。
-
数学建模:将问题转化为数学模型。我们将使用整数规划方法来确定最佳的站点位置。假设我们有 n 个需求点和 m 个候选站点。令 x(i) 表示候选站点 i 是否被选择,如果是则为 1,否则为 0。令 y(i, j) 表示从需求点 i 到候选站点 j 的运输量。
目标函数:最小化总体运输成本,即 min ΣΣ c(i, j) * y(i, j),其中 c(i, j) 表示从需求点 i 到候选站点 j 的运输成本。
约束条件:文章来源:https://www.toymoban.com/news/detail-777927.html- 每个需求点必须被一个站点服务:Σ x(i) = 1,对所有 i。
- 运输量必须满足需求:Σ y(i, j) = d(i),对所有 i。
- 候选站点的选择变量为二进制:x(i) ∈ {0, 1},对所有 i。
- 运输量的取值范围为非负整数:y(i, j) ≥ 0,对所有 i 和 j。
-
编程实现:使用 MATLAB 编程实现以上数学模型。文章来源地址https://www.toymoban.com/news/detail-777927.html
% 数据准备到了这里,关于鲜奶配送站点的最优化设置问题 - MATLAB 实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!