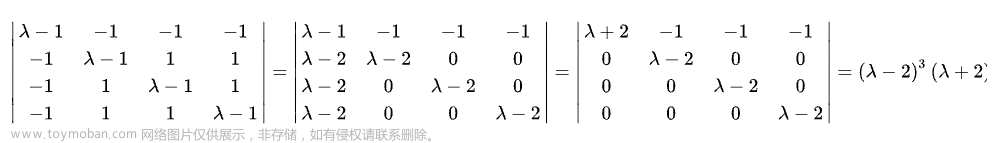C语言——利用矩阵LU分解法求逆、行列式-Toy模板网

这篇具有很好参考价值的文章主要介绍了C语言——利用矩阵LU分解法求逆、行列式。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本章介绍了LU分解法，以及如何利用LU分解法求逆、行列式，针对每个公式、原理、代码进行了详细介绍，希望可以给大家带来帮助。

LU分解法与高斯法求逆一样，可以进行较高维数的矩阵运算（可计算万维及以上，但是精度不能保证，并且占有内存大，高维矩阵需要进行分块运算）

更改：

之前的代码使用_msize函数求矩阵维数，然而_msize函数只适用于windows，提供了一种可移植度高的版本。

之前在计算L、U的逆矩阵时，使用的是高斯求逆法，没有充分利用L、U矩阵的特性，已更改。

修改了选主元时的bug。

LU分解法

概念

确定L、U矩阵

求L、U的逆矩阵

LU分解法的意义

程序设计

LUP求逆

1）结构体定义与头文件

2）辅助函数

3）矩阵乘法

4） LU求逆函数

测试

整数矩阵计算：

浮点矩阵计算：

LUP求行列式

LU分解法

概念

将系数矩阵A转变成等价两个矩阵L和U的乘积，其中L和U分别是单位下三角矩阵和上三角矩阵。当A的所有顺序主子式都不为0时，矩阵A可以唯一地分解为A=LU。其中L是下三角矩阵（主对角线元素为1），U是上三角矩阵。

于是，对矩阵A求逆就变成了：

因为LU分别为下三角矩阵和上三角矩阵，再进行高斯变换求逆矩阵时，浮点运算的复杂度将减少一半。

对矩阵A求其行列式的值变成：

因为L的主对角元素全1，故 A的行列式的值等于U主对角线元素的乘积。

确定L、U矩阵

因为矩阵L的主对角元素定死为1，因此可以通过矩阵乘法原理，逐行、逐列的逆推出矩阵L和U的元素

方法如下：

确定U的第一行
确定L的第一列
确定U的第二行
确定L的第二列
...
确定U的第n行
确定L的第n列

确定U的第一行：

L的第一行与U的第一列对应元素相乘再相加，结果等于，即：
L的第一行与U的第二列对应元素相乘再相加，结果等于，即：
不难看出，U的第一行与A的第一行元素相同：

确定L的第一列：

L每列的首元素都为1，从第二个元素开始判断
L的第二行与U的第一列对应元素相乘再相加，结果等于，即：
L的第三行与U的第一列对应元素相乘再相加，结果等于，即：
故，L的第一列为：

仿照上述步骤，即可求出L、U，整理公式如下：

$lu分解求逆矩阵,# C语言线性代数,矩阵,线性代数,算法,c语言,开发语言$

在进行代码设计时，求和部分可用for循环单独计算，存储到变量a中，变量a需初始化为0，当i=0时，不满足for循环条件，a=0，即可推出上述U的第一行和L的第一列。

LU分解法的推导与验证请参考相关数值分析教材，推荐参考博客矩阵的直接LU分解法

求L、U的逆矩阵

由于L、U矩阵自身的特性，这时我们可以通过L、U矩阵直接逆推出其逆矩阵，无需再用高斯求逆，逆推思想与上述思想类型，这里直接给出下三角矩阵和上三角矩阵求逆公式：

对于下三角矩阵：

对于上三角矩阵：

$lu分解求逆矩阵,# C语言线性代数,矩阵,线性代数,算法,c语言,开发语言$

需要注意：上述公式是基于程序设计的思维，也就是我们对L、U矩阵本身进行改动，使其变成各自的逆矩阵，这样就无需再开辟新的内存空间。

计算下三角矩阵的逆时，我们是按行，从第1行到第n行开始计算，第一行第一列，第二行第一列，第二行第二列，以此类推。
计算上三角矩阵的逆时，我们是按列，从第n列到第1列开始计算，第n列第n行，第n列第n-1行，以此类推。
二者的计算次序正好相反，该点在代码设计中也有所体现。

LU分解法的意义

LU具有承袭性，这是LU的优点。

LU只适用于解所有顺序主子式都大于0的，通用性欠缺，这是LU的缺点。

LU法不保证具有数值稳定性，这是LU的缺点。（Gauss法可以用选取列主元技巧保证数值稳定性）

集合LU与Gauss优点，同时规避掉这些缺点的，是LUP分解法。

作者：寨森Lambda-CDM

我个人的理解是：计算机在处理超维矩阵时（例如一万维），会采用分块矩阵的方式进行求解，通过先分块再LU，将矩阵分成一块块下三角矩阵和上三角矩阵存储起来，在后续其他计算中，直接调用下三角矩阵和上三角矩阵计算的效率更高。（该部分我也在学习，欢迎大家讨论）

程序设计

该部分程序实际上是LUP分解法，增加了选择主元的过程，因为在分解LU以及高斯消元求逆时，如果主元的元素是0，那么计算机将无法计算，所以在分解前需先选择主元。

在矩阵设计时，最开始使用的是_msize函数通过内存计算矩阵的维数，而在后来使用Linux和Mac系统后，发现不支持_msize函数，同时又不想每次计算时都输入矩阵的维数，因此设计一个结构体来存储矩阵。（_msize函数只支持windows，我的其他博客有相关介绍：判断矩阵维数）

整体流程如下：

检查是否符合计算要求
保护原矩阵，进行临时矩阵的拷贝
选择主元
构建L、U矩阵
计算L、U矩阵的逆（如果求行列式，无需求逆，直接求U矩阵主对角线的乘积）
利用矩阵乘法求得最终结果
释放内存

LUP求逆

1）结构体定义与头文件

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include <time.h>
#include <math.h>

typedef struct Matrix
{
    int row;
    int col;
    double **data;
} Matrix;

2）辅助函数

// 创建矩阵
Matrix MakeMatrix(int row, int col)
{
    int i = 0;
    Matrix arr = {0};
    arr.row = row;
    arr.col = col;
    arr.data = (double **)malloc(sizeof(double *) * arr.row);
    if (arr.data == NULL)
        exit(-1);
    for (i = 0; i < arr.row; i++)
    {
        arr.data[i] = (double *)malloc(sizeof(double) * arr.col);
        memset(arr.data[i], 0, sizeof(double) * arr.col);
    }
    return arr;
}

// 释放矩阵内存
void free_Matrix(Matrix src)
{
    int i;
    for (i = 0; i < src.row; i++)
    {
        free(src.data[i]);
    }
    free(src.data);
}

// 打印矩阵
void print_Matrix(Matrix arr)
{
    int i, j;
    putchar('\n');
    for (i = 0; i < arr.row; i++)
    {
        for (j = 0; j < arr.col; j++)
        {
            printf("%10.4lf ", arr.data[i][j]);
        }
        putchar('\n');
    }
}

// 生成随机矩阵
void rand_Matrix(Matrix arr)
{
    int i, j;
    double num, res, res1, res2 = 0;
    srand((unsigned int)time(NULL));
    for (i = 0; i < arr.row; i++)
    {
        for (j = 0; j < arr.col; j++)
        {
            //随机生成整数
            /* num = pow(-1, rand() % 2 + 1) * (rand() % 20);
            arr.data[i][j] = num; */

            //4位浮点数
            res1 = res2 = 0;
            while (res1 == 0)
            {
                res1 = pow(-1, rand() % 2 + 1) * (rand() % 101);
                res2 = pow(-1, rand() % 2 + 1) * (rand() % (int)(1e4));
            }
            res = res1 + (res2 * 1e-4);
            arr.data[i][j] = res;
        }
    }
}

上述辅助函数需要注意两点：

释放内存时，先便利释放每一行的内存，最终将整个data内存释放掉。
创建随机矩阵时，srand函数用于修饰rand，以time为标准生成随机数。
这里创建浮点数的思想为：1）创建一个范围在[-100,100]内的整数。2）创建一个范围在[0,1000)内的整数，然后对其除以10的-4次方，使其变成小数部分。3）将二者相加，即得到了小数点后4位的随机数。（创建随机矩阵时，笔者之前使用的是将两个整数做除法，但该种做法无法与matlab结果验证）

3）矩阵乘法

矩阵乘法较为简单，笔者在C语言矩阵乘法中介绍了其原理，以及多种程序设计思路，这里不再赘述。

Matrix Matrix_Mul(const Matrix left, const Matrix right)
{
    if (left.col != right.row)
        exit(-1); // 判断左列是否等于右行
    int i, j, k;
    Matrix res = MakeMatrix(left.row, left.row);
    for (i = 0; i < left.row; i++)
    {
        for (j = 0; j < right.col; j++)
        {
            for (k = 0; k < left.col; k++)
            {
                res.data[i][j] += left.data[i][k] * right.data[k][j]; 
            }
        }
    }
    return res;
}

4） LU求逆

Matrix Matrix_LU_Inv(Matrix src)
{
    assert(src.row == src.col);
    int i, j, k, principal;
    Matrix L, U, tmp, res;
    double Lsum, Usum, p, Max;
    L = MakeMatrix(src.row, src.col);
    U = MakeMatrix(src.row, src.col);
    tmp = MakeMatrix(src.row, src.col);
    for (i = 0; i < src.row; i++)
    {
        memcpy(tmp.data[i], src.data[i], sizeof(src.data[0][0]) * src.col);
    }
    // 初始化斜对角线
    for (i = 0; i < L.row; i++)
    {
        for (j = 0; j < L.col; j++)
        {
            if (i == j)
                L.data[i][j] = 1; // L主对角线为1
        }
    }
    // 选主元
    for (j = 0; j < tmp.col; j++)
    {
        // 默认当前主元最大
        principal = j;
        Max = fabs(tmp.data[principal][j]); // 用绝对值比较
        // 只遍历当前主元下方的元素
        for (i = j + 1; i < tmp.row; i++)
        {
            if (fabs(tmp.data[i][j]) > Max)
            {
                principal = i;
                Max = fabs(tmp.data[i][j]);
            }
        }
        if (j != principal)
        {
            for (k = 0; k < tmp.col; k++)
            {
                p = tmp.data[principal][k];
                tmp.data[principal][k] = tmp.data[j][k]; // 交换两行
                tmp.data[j][k] = p;
            }
        }
    }
    // 计算L、U
    for (i = 0; i < tmp.row; i++)
    {
        for (j = 0; j < tmp.col; j++)
        {
            if (i < 1 && j < 1)
            {
                U.data[i][j] = tmp.data[i][j];
            }
            else if (i <= j)
            {
                Usum = 0;
                for (k = 0; k < i; k++)
                {
                    Usum += L.data[i][k] * U.data[k][j]; // 计算求和部分
                }
                U.data[i][j] = tmp.data[i][j] - Usum;
            }
            else
            {
                Lsum = 0;
                for (k = 0; k < j; k++)
                {
                    Lsum += L.data[i][k] * U.data[k][j]; // 计算求和部分
                }
                L.data[i][j] = (tmp.data[i][j] - Lsum) / U.data[j][j];
            }
        }
    }
    free_Matrix(tmp);
    //L求逆
    for (i = 0; i < L.row; i++)
    {
        for (j = 0; j <= i; j++)
        {
            if (i == j)
            {
                L.data[i][j] = 1.0 / L.data[i][j];
            }
            else
            {
                Lsum = 0;
                for (k = j; k < i; k++)
                {
                    Lsum += L.data[i][k] * L.data[k][j];
                }
                L.data[i][j] = -1.0 * Lsum / L.data[i][i];
            }
        }
    }
    // U求逆
    for (j = U.col - 1; j >= 0; j--)
    {
        for (i = j; i >= 0; i--)
        {
            if (i == j)
            {
                U.data[i][j] = 1.0 / U.data[i][j];
            }
            else
            {
                Usum = 0;
                for (k = j; k >= i + 1; k--)
                {
                    Usum += U.data[i][k] * U.data[k][j];
                }
                U.data[i][j] = -1.0 * Usum / U.data[i][i];
            }
        }
    }
    res = Matrix_Mul(U, L); // 乘法
    free_Matrix(L), free_Matrix(U);
    return res;
}

测试

void LU_inv_test()
{
    Matrix arr = MakeMatrix(3, 3);
    rand_Matrix(arr);
    print_Matrix(arr);
    Matrix res = Matrix_LU_Inv(arr);
    print_Matrix(res);
    Matrix res2 = Matrix_Guass_inver(arr);
    print_Matrix(res2);
}
int main()
{
    LU_inv_test();
    return 0;
}

整数矩阵计算：

C语言计算结果：

lu分解求逆矩阵,# C语言线性代数,矩阵,线性代数,算法,c语言,开发语言

Matlab计算结果：

lu分解求逆矩阵,# C语言线性代数,矩阵,线性代数,算法,c语言,开发语言

显然，二者计算的结果是等价的。

浮点矩阵计算：

C语言计算结果：

lu分解求逆矩阵,# C语言线性代数,矩阵,线性代数,算法,c语言,开发语言

Matlab计算结果：

lu分解求逆矩阵,# C语言线性代数,矩阵,线性代数,算法,c语言,开发语言

显然，二者也是等价的。有兴趣的同学可以尝试创建一万维的矩阵进行运算，该方法也是能够计算的，当然会牺牲一些内存。

矩阵求逆时只涉及到简单的加减乘除运算，运算结果与matlab结果并无差异。而涉及到复杂的浮点数的运算，C语言的计算精度稍显不足。例如：C语言中sqrt开方的处理，与Fortran中的处理就略有差别。对于精度较高的运算，笔者认为使用Fortran是个不错的选择，或者使用各大机构发布的数值运算库（例如Intel OneAPI的mkl库）。
对于极小或者极大的数，可以考虑加入缩放因子来提高精度。在计算LU矩阵前对原矩阵进行放大，每个元素乘以缩放因子beta，得到逆矩阵同样乘以beta即可。（本文算例不需要加入缩放因子，故所以上文就没有提及)

LUP求行列式

行列式的求法相对简单，依据前文的公式，最后只需要对U矩阵对主对角线求乘积即可。这里给出代码，各位同学请自行测试。

#include "matrix.h"

double Matrix_LU_Det(Matrix src)
{
    assert(src.row == src.col);
    int i, j, k, principal;
    Matrix L, U, tmp, res;
    double Lsum, Usum, p, Max;
    L = MakeMatrix(src.row, src.col);
    U = MakeMatrix(src.row, src.col);
    tmp = MakeMatrix(src.row, src.col);
    for (i = 0; i < src.row; i++)
    {
        memcpy(tmp.data[i], src.data[i], sizeof(src.data[0][0]) * src.col);
    }
    // 初始化斜对角线
    for (i = 0; i < L.row; i++)
    {
        for (j = 0; j < L.col; j++)
        {
            if (i == j)
                L.data[i][j] = 1; // L主对角线为1
        }
    }
    // 选主元
    for (j = 0; j < tmp.col; j++)
    {
        // 默认当前主元最大
        principal = j;
        Max = fabs(tmp.data[principal][j]); // 用绝对值比较
        // 只遍历当前主元下方的元素
        for (i = j + 1; i < tmp.row; i++)
        {
            if (fabs(tmp.data[i][j]) > Max)
            {
                principal = i;
                Max = fabs(tmp.data[i][j]);
            }
        }
        if (j != principal)
        {
            for (k = 0; k < tmp.col; k++)
            {
                p = tmp.data[principal][k];
                tmp.data[principal][k] = tmp.data[j][k]; // 交换两行
                tmp.data[j][k] = p;
            }
        }
    }
    // 计算L、U
    for (i = 0; i < tmp.row; i++)
    {
        for (j = 0; j < tmp.col; j++)
        {
            if (i < 1 && j < 1)
            {
                U.data[i][j] = tmp.data[i][j];
            }
            else if (i <= j)
            {
                Usum = 0;
                for (k = 0; k < i; k++)
                {
                    Usum += L.data[i][k] * U.data[k][j]; // 计算求和部分
                }
                U.data[i][j] = tmp.data[i][j] - Usum;
            }
            else
            {
                Lsum = 0;
                for (k = 0; k < j; k++)
                {
                    Lsum += L.data[i][k] * U.data[k][j]; // 计算求和部分
                }
                L.data[i][j] = (tmp.data[i][j] - Lsum) / U.data[j][j];
            }
        }
    }
    free_Matrix(tmp);
    p = 1;
    for (i = 0; i < U.row; i++)
    {
        for (j = 0; j < U.col; j++)
        {
            if (i == j)
                p *= U.data[i][j];
        }
    }
    free_Matrix(L), free_Matrix(U);
    return p;
}

结语：

通过上述的实验，我们发现单纯C语言设计矩阵运算时有些劣势，代码有些冗余而且不易阅读，这些问题将在C++中得到解决，以利用C++将上述结构体与函数统一归为类，然后利用函数重载，优化代码的可阅读性。文章来源地址https://www.toymoban.com/news/detail-778659.html

到了这里，关于C语言——利用矩阵LU分解法求逆、行列式的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！