1. 什么是稀疏矩阵
在矩阵中,若数据为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反的叫做稠密矩阵。
2. 稀疏矩阵的应用场景

将棋盘看作一个二维数组,在棋子落盘时,要记录该棋子落下的坐标,其他坐标的值不做记录,默认为0。由于记录很多无意义的数据,原始的二维数组不能直观的显示棋盘上棋子的落盘状态,需要用一种简化的显示方法。
示例:
3. 稀疏矩阵的存储方式
存储矩阵的一般方法是采用二维数组,其优点是可以随机地访问每一个元素。因而能够实现矩阵的各种运算。但对于稀疏矩阵而言,会重复存储多个无效元素,这大大浪费了内存空间,而且不方便查看有效数据的位置,花费大量时间来进行行列元素的无效计算。所以必须考虑对稀疏矩阵进行压缩存储。
当一个数组中大部分元素为0,或者为同一个值的数组值,可以使用稀疏数组来保存该数组
稀疏数组的处理方法是:
● 记录数组一共有几行几列,有多少个不同的值。
● 把具有不同值的元素的行列记录在一个小规模的数组中,从而缩小程序的规模
4. 稀疏矩阵的压缩存储方式
稀疏矩阵的压缩存储,又称稀疏矩阵的转置。
4.1 三元组
三元组(也叫COO(Coordinate Format))。
在三元组中,稀疏矩阵的压缩存储,至少需要存储以下信息:
矩阵中各非零元素的值,以及所在矩阵中的行标和列表。
矩阵的总行数和列数

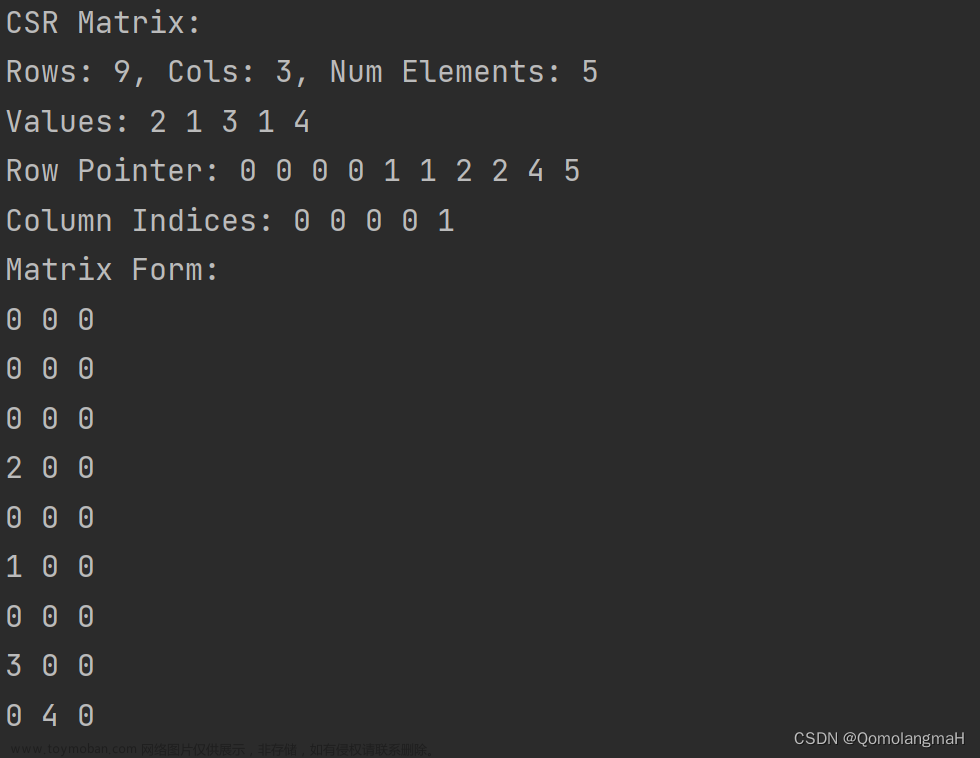
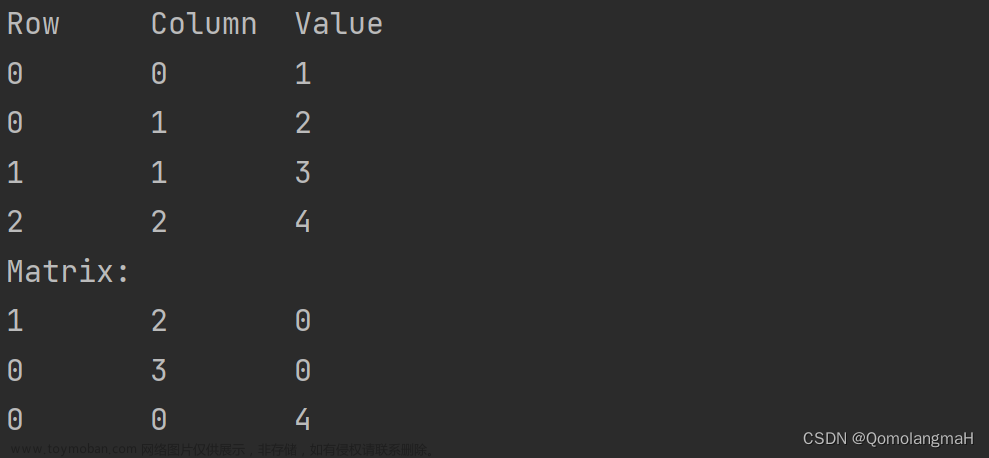
例如一个稀疏矩阵:
压缩后的三元组为:
其中第二表示一个稀疏矩阵的行列总数,以及非零数据的个数。
这样,一个三行四列的稀疏矩阵用三元表就表示了出来。
4.2 行逻辑链接的顺序表
行逻辑链接的顺序表,它可以看作是三元组顺序表的升级版,即在三元组顺序表的基础上改善了提取数据的效率。
行逻辑链接的顺序表和三元组顺序表的实现过程类似,它们存储矩阵的过程完全相同,都是将矩阵中非0元素的三元组(行标,列标和元素值)存储在一维数据中。但是为了提高提取数据的效率,前者在存储矩阵时比后者多使用了一个数组,专门记录矩阵中每行第一个非0元素在一维数组中的位置。
当使用行逻辑链接的顺序表对其进行压缩存储时,需要做以下两个工作:
将矩阵的非0元素采用三元组的形式存储到一维数组data中
使用rpos记录矩阵中每行第一个非0元素在三元表中的存储位置。
通过以上两步操作,即实现了使用行逻辑链接的顺序表存储稀疏矩阵。
此时,如果想从行逻辑链接的顺序表中提取元素,则可以借助rpos数组提高遍历数组的效率。
例如,提取上述稀疏矩阵中的元素2的过程如下:
●由 rpos 数组可知,第一行首个非 0 元素位于data[0]( chessArr[sparseArr[0][0]][sparseArr[0][1]] ),因此在遍历此行时,可以直接从第 data[1] 的位置开始,一直遍历到下一行首个非 0 元素所在的位置(data[2])之前;
●同样遍历第二行时,由 rpos 数组可知,此行首个非 0 元素位于 data[2] ( chessArr[sparseArr[2][0]][sparseArr[2][1]] ),因此可以直接从第 data[2] 开始,一直遍历到下一行首个非 0 元素所在的位置(data[3])之前;
●遍历第三行时,由 rpos 数组可知,此行首个非 0 元素位于 data[3] ( chessArr[sparseArr[3][0]][sparseArr[3][1]] ),由于这是矩阵的最后一行,因此一直遍历到 rpos 数组结束即可(也就是 num,num指的是矩阵非 0 元素的总个数)。
用代码根据给出的行逻辑顺序表构造稀疏矩阵:
实现思路:用稀疏矩阵中的每一个值与三元组表中的值匹配,三元组的值通过行逻辑表直接访问,将每个稀疏矩阵中的值与三元表中存放的非0数值进行匹配,直到与该行所有非0数值匹配完毕。依次循环,和每行的非零数值进行匹配,若匹配成功,则将该非0数值记录在当前稀疏矩阵的坐标下,否则记录0。
class Triple{
int MaxSize=10086;
int [][] sparseArr=new int[10086][10086];
}
class RLMatrix extends Triple{
int MaxRc=100;
int [] rpos=new int[MaxRc];
int row,col,num;//行数,列数,元素个数
public RLMatrix(int row,int col,int num){
this.row=row;
this.col=col;
this.num=num;
}
void display() {
for(int i=0;i<row;i++) {
for(int j=0;j<col;j++) {
int value=0;//设置一个访问标志,用来记录当当前是否遍历到非0数值
if(i+1<row) {
for(int k=rpos[i];k<rpos[i+1];k++) {//遍历本行所有非零元素的值
if(i==sparseArr[k][0]&&j==sparseArr[k][1]) {
// k记录首行非零元素在三元组中的行号,叠加二维数组得到首行非零元素在矩阵中的坐标
System.out.print(sparseArr[k][2]+" ");
// 若此时的i,j坐标与三元组中记录该值的行标,列标相同,打印三元组中的该数值。
value=1;
// value值变成1,表示此次循环匹配到非0数值
break;
// 当前i,j与三元组中记录的值匹配完毕,跳出该层循环,与三元组中记录本行的下一个数值进行匹配
}
}
if(value==0) {
// 当上述循环结束时,若始终没有匹配到非0数值,则value值没有发生变化,仍然为0
System.out.print("0 ");
}
}
else {
// 当循环进行到该矩阵的最后一行时,只需要从本行非0元素遍历到最后一个元素即可
for(int k=rpos[i];k<num;k++) {
if(i==sparseArr[k][0]&&j==sparseArr[k][1]) {
System.out.print(sparseArr[k][2]+" ");
value=1;
break;
}
}
if(value==0) {
System.out.print("0 ");
}
}
}
System.out.println();
}
}
}
public class LineSparseArray{
public static void main(String urgs[]){
RLMatrix M=new RLMatrix(3,4,4);
// 在三元组中记录矩阵中非零元素的信息
M.sparseArr[0][0]=0;
M.sparseArr[0][1]=1;
M.sparseArr[0][2]=3;
M.sparseArr[1][0]=0;
M.sparseArr[1][1]=3;
M.sparseArr[1][2]=5;
M.sparseArr[2][0]=1;
M.sparseArr[2][1]=2;
M.sparseArr[2][2]=1;
M.sparseArr[3][0]=2;
M.sparseArr[3][1]=0;
M.sparseArr[3][2]=2;
// 在行逻辑表中记录三元组中记录的稀疏矩阵中的首行非零元素在三元组中的信息的位置
M.rpos[0]=0;
M.rpos[1]=2;
M.rpos[2]=3;
M.display();
}
}
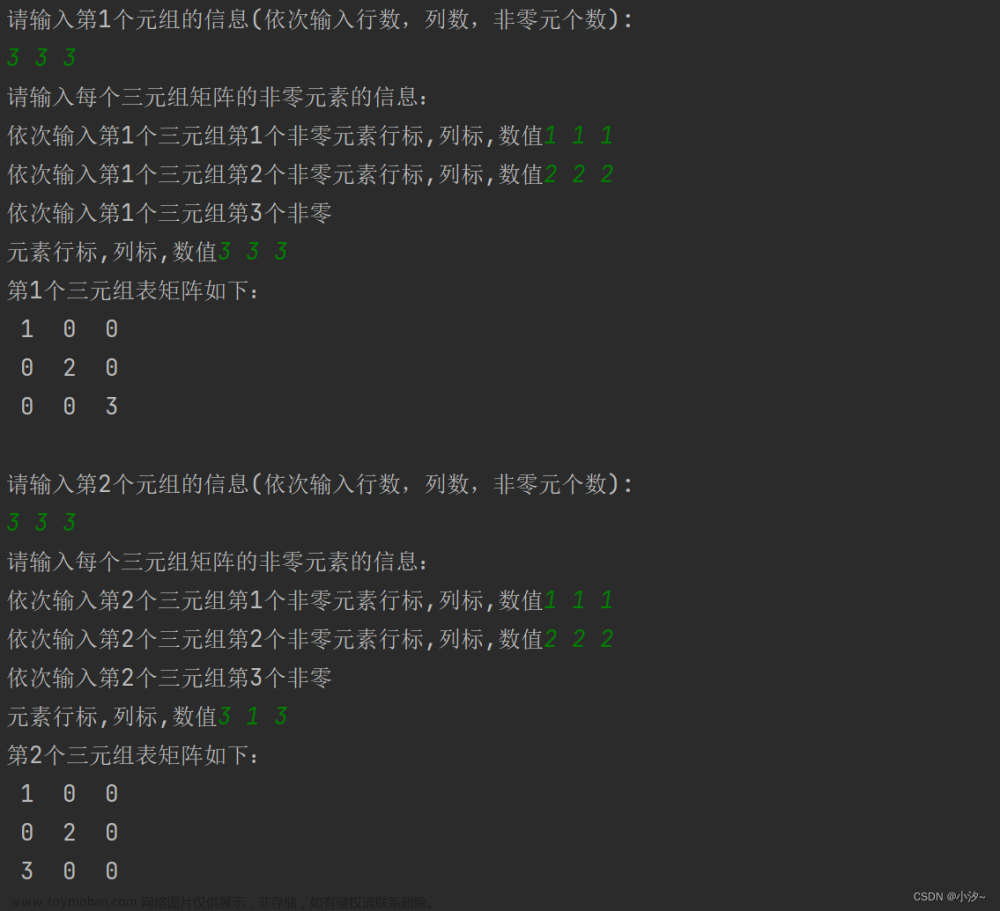
程序运行示意图

5. 三元组表示法简单实现稀疏矩阵的压缩存储与还原
5.1 压缩稀疏矩阵
首先定义一个二维数组,并赋予若干个非零数值。
int chessArr1[][]=new int[11][11];
chessArr1[1][2]=1;
chessArr1[2][4]=1;

定义一个稀疏数组,稀疏数组的第一行输出的是行列总数与非零值个数。
int sparseArr[][]=new int[3][3];
sparseArr[0][0]=11;
sparseArr[0][1]=11;
sparseArr[0][2]=sum; // 遍历二维数组,将非0值存放到稀疏数组
int count=0;//count用来计算非零数组的个数,根据非零数值在稀疏矩阵中的个数添加行数
for(int i=0;i<11;i++)
for(int j=0;j<11;j++)
if(chessArr1[i][j]!=0) {
count++; //当遍历到非零数值时,count+1,从第二行开始记录行列号
sparseArr[count][0]=i;
sparseArr[count][1]=j;
sparseArr[count][2]=chessArr1[i][j]; //表示第三列是该非零数值自身
}

5.2 将稀疏数组还原为二维数组
1.根据稀疏数组第一行的数据得到二维数组的大小,创建二维数组
2.根据稀疏数组的后几行数据得到非0值所在的行列,并将数值赋值到所在的行列
int chessArr2[][]=new int[sparseArr[0][0]][sparseArr[0][1]];//根据第一行的数值还原二位数组的大小

for(int i=1;i<sparseArr.length;i++)
chessArr2[sparseArr[i][0]][sparseArr[i][1]]=sparseArr[i][2];
// 赋值后的二维数组
System.out.println("还原后的二维数组");
for(int[] row: chessArr2) {
for(int data:row) {
System.out.printf("%d\t",data);
}
System.out.println();
}

稀疏数组中的行值,列值就是该数值的行列号,对应二维数组的下标,得到该坐标的非零数值。
给出完整的代码:
public class sparseArray {
public static void main(String[] args) {
//创建一个原始的二维数组
// 0:表示没有棋子 1:表示有棋子;
int chessArr1[][]=new int[11][11];
chessArr1[1][2]=1;
chessArr1[2][4]=1;
//输出原始的二维数组
System.out.println("原始的二维数组:");
for(int[] row: chessArr1) {//增强型for循环
for(int data:row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
int sum = 0;
//将二维数组 转为 稀疏数组
//先遍历,得到有效数据的个数
for(int i=0;i<11;i++)
for(int j=0;j<11;j++)
if(chessArr1[i][j]!=0)
sum++;
//创建对应的稀疏数组
int sparseArr[][]=new int[3][3];
sparseArr[0][0]=11;
sparseArr[0][1]=11;
sparseArr[0][2]=sum; // 遍历二维数组,将非0值存放到稀疏数组
int count=0;//count用来计算非零数组的个数,根据非零数值在稀疏矩阵中的个数添加行数
for(int i=0;i<11;i++)
for(int j=0;j<11;j++)
if(chessArr1[i][j]!=0) {
count++;
sparseArr[count][0]=i;
sparseArr[count][1]=j;
sparseArr[count][2]=chessArr1[i][j];
}
System.out.println("转换后的稀疏数组为:");
for(int i=0;i<sparseArr.length;i++)
{
System.out.printf("%d\t%d\t%d\t",sparseArr[i][0],sparseArr[i][1],sparseArr[i][2]);
System.out.println();
}
//将稀疏数组还原为二维数组
// 1.根据稀疏数组第一行的数据得到二维数组的大小,创建二维数组
// 2.根据稀疏数组的后几行数据得到非0值所在的行列,并将数值赋值到所在的行列
int chessArr2[][]=new int[sparseArr[0][0]][sparseArr[0][1]];
System.out.println("还原后的初始二维数组:");
for(int[] row: chessArr2) {//增强型for循环
for(int data:row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
for(int i=1;i<sparseArr.length;i++)
chessArr2[sparseArr[i][0]][sparseArr[i][1]]=sparseArr[i][2];
// 数值后的二维数组
System.out.println("还原后的二维数组");
for(int[] row: chessArr2) {
for(int data:row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
}
}
这样,一个简单的稀疏矩阵的压缩与还原就成功实现了。
6. 稀疏矩阵的转置
一个MN的矩阵A,它的转置矩阵B是一个NM的矩阵,且满足aij=bij。
如下图所示,矩阵B就是矩阵A的转置矩阵。
矩阵A:
(
0
5
0
0
7
1
5
3
0
0
0
6
0
0
0
)
\left( \begin{matrix} 0 & 5 & 0 &0 & 7\\ 1 & 5 & 3 & 0 & 0 \\ 0 & 6 & 0 & 0 & 0 \end{matrix} \right)
⎝⎛010556030000700⎠⎞
矩阵B:
(
0
1
0
5
5
6
0
3
0
0
0
0
7
0
0
)
\left( \begin{matrix} 0 & 1 & 0 \\ 5 & 5 & 6 \\ 0 & 3 & 0 \\ 0 & 0 & 0 \\ 7 & 0& 0 \end{matrix} \right)
⎝⎜⎜⎜⎜⎛050071530006000⎠⎟⎟⎟⎟⎞
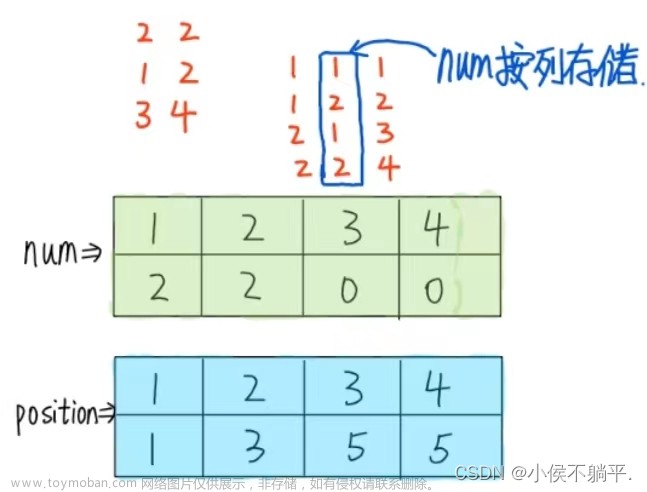
对于矩阵A和矩阵B来说,其各自用三元组顺序表表示,如下图所示:

在三元组表的存储形式下,求稀疏矩阵 A 的转置矩阵 B ,实际上就是求由 a 得到 b:
由 a 的行数、列数以及非 0 元素数可以直接得到 b 的列数、行数和非 0 元素数。
由 a 中的数据得到 b 中的数据,可采用两种方法实现:
● 对 a 中的数据进行遍历,即依次扫描第 0 列、第 1 列、……、最后一列,扫描过程交换行和列的顺序,并存储到 b 中对应的位置即可。
● 要想扫描一次 a 就能得到 b,必须每次扫描到一个三元组就直接将其放到 b 中相应的位置上,因此,需要知道 a 中的元素在 b 中的存储位置,这就要预先确定矩阵 A 的每一列的第一个非 0 元素在 b 中相应的位置。为此,需要附设两个数组,num 和cpot,分别用于存储矩阵 A 中每一列的非 0 元素个数和矩阵 A 中每一列第 1 个非0 元素在 b 中的存储位置。
显然,有如下的公式成立:
cpot[0] = 1
cpot[col] = cpot[col - 1] + num[col -1],col 取大于等于 1 且小于 n 的数
所以,图 1 中的矩阵 A ,其 num 和 cpot 数组的值为:

6.1 稀疏矩阵的一般转置方法
import java.util.Scanner;
class TcrMatrix {
int row;//行数
int col;//列数
int count;//矩阵中非零值的个数
int [][]sparseArr;
int [][] chessArr;
public TcrMatrix(int row, int col, int count) {
this.row = row;
this.col = col;
this.count = count;
sparseArr=new int[count][3];
}
void input() {//输入矩阵中非零元素在三元组表中的值
Scanner sc = new Scanner(System.in);//输入稀疏矩阵三元组的值
for (int i = 0; i < count; i++) {//矩阵中非零数值的个数与三元组的行数一致
sparseArr[i][0] = sc.nextInt();
sparseArr[i][1] = sc.nextInt();
sparseArr[i][2] = sc.nextInt();
}
}
void dispalya(){//打印给出的三元组表
for (int i = 0; i < count; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(sparseArr[i][j]+" ");
}
System.out.println();
}
}
void chessArr() {//由三元组表还原稀疏矩阵
chessArr=new int[row][col];
int value=0;//设置访问标志
for(int i=0;i<row;i++)
for(int j=0;j<col;j++) {
for(int k=0;k<count;k++) {
if(i==sparseArr[k][0]&&j==sparseArr[k][1]) {
chessArr[i][j] = sparseArr[k][2];
value=1;
}
if(value==0){//如果该坐标与三元组中记录的所有非零数组坐标不同,value仍然为0,表示三元组中没有与之相对应的非零数值
chessArr[i][j]=0;//此处也可以省略不写,因为数组创建时默认为0
}
}
}
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
System.out.print(chessArr[i][j]+" ");
}
System.out.println();
}
}
void printTranposition(){//打印转置后的稀疏矩阵
for (int i = 0; i < col; i++) {
for (int j = 0; j < row; j++) {
System.out.print(chessArr[j][i]+" ");
}
System.out.println();
}
}
}
public class trsMatrix {
public static void main(String[] args) {
TcrMatrix t=new TcrMatrix(3,5,6);
System.out.println("输入稀疏矩阵的三元组表:");
t.input();
System.out.println("输出稀疏矩阵的三元组表:");
t.dispalya();
System.out.println("根据给出的三元组表还原稀疏矩阵:");
t.chessArr();
System.out.println("转置后的稀疏矩阵:");
t.printTranposition();
}
}

6.2 稀疏矩阵的快速转置算法
稀疏矩阵的快速转置,只需要在源代码基础上稍作修改。
定义一nums数组,用来记录矩阵A中每一列的非零数值。
int maxsize = 50;
int[] num = new int[maxsize];
int[] cpot = new int[maxsize];
sparseArr1 = new int[count][3];
cpot[0] = 0;//矩阵第一列非零元素值在三元组表b中的位置
if (count != 0) {
for (int i = 0; i < count; i++) {
num[sparseArr[i][1]]++;//只要访问到同一列的非零数值,num该位置的数值+1
}
cpot数组用来记录矩阵A中每列的第一个非零数值,cpot与num数组存下以下的关系式:
cpot[0] = 0;//矩阵第一列非零元素值在三元组表b中的位置
for (int i = 1; i < count; i++) {
cpot[i] = cpot[i - 1] + num[i - 1];
}
实现三元组a向三元组b的转换:
for (int i = 0; i < count; i++) {
int col = sparseArr[i][1];
int q = cpot[col];//记录在三元组B中的位置
sparseArr1[q][1] = sparseArr[i][0];//将三元组a中对应费零数值的信息存储在三元组b中,但是i,j的值发生调换,三元组a中的列号为三元组a中的行号
sparseArr1[q][0] = sparseArr[i][1];
sparseArr1[q][2] = sparseArr[i][2];
cpot[col]++;//当在三元组a中在同一列再次访问不同的数据时,该列访问的上一个元素的位置+1,表示在三元组b的存储位置上紧挨上一个与自己同列的数值,在该列继续向下存储数据
//指针对矩阵a中每列有多个非零数值,当该列只有一个非零数值时,该表达式不起任何效果,因为不会访问到该列的下一个非零数值
}
完整的代码如下:文章来源:https://www.toymoban.com/news/detail-778693.html
import java.util.Scanner;
class TcrMatrix1 {
int row;//行数
int col;//列数
int count;//矩阵中非零值的个数
int[][] sparseArr;//三元组存储表a
int[][] sparseArr1;//三元组存储表b
int[][] chessArr;
int[][] chessArr1;
public TcrMatrix1(int row, int col, int count) {
this.row = row;
this.col = col;
this.count = count;
sparseArr = new int[count][3];
}
void input() {
Scanner sc = new Scanner(System.in);
for (int i = 0; i < count; i++) {
sparseArr[i][0] = sc.nextInt();
sparseArr[i][1] = sc.nextInt();
sparseArr[i][2] = sc.nextInt();
}
}
void display() {
for (int i = 0; i < count; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(sparseArr[i][j] + " ");
}
System.out.println();
}
}
void chessArr() {
chessArr = new int[row][col];
for (int i = 0; i < sparseArr.length; i++) {
chessArr[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
for(int[] col: chessArr) {
for(int data:col) {
System.out.printf("%d\t",data);
}
System.out.println();
}
}
void FastTranposition() {
int maxsize = 50;
int[] num = new int[maxsize];
int[] cpot = new int[maxsize];
sparseArr1 = new int[count][3];
cpot[0] = 0;//矩阵第一列非零元素值在三元组表b中的位置
if (count != 0) {
for (int i = 0; i < count; i++) {
num[sparseArr[i][1]]++;
}
System.out.println("输出矩阵A中各列的非零元素个数");
for (int i = 0; i < col; i++) {
System.out.print(num[i] + " ");
}
System.out.println();
for (int i = 1; i < count; i++) {
cpot[i] = cpot[i - 1] + num[i - 1];
}
System.out.println("矩阵A中各列第一个非零值在三元组表B中的位置");
for (int i = 0; i < col; i++) {
System.out.print(cpot[i] + " ");
}
System.out.println();
}
System.out.println();
for (int i = 0; i < count; i++) {
int col = sparseArr[i][1];
int q = cpot[col];//记录在三元组B中的位置
sparseArr1[q][1] = sparseArr[i][0];//将三元组a中对应费零数值的信息存储在三元组b中,但是i,j的值发生调换,三元组a中的列号为三元组a中的行号
sparseArr1[q][0] = sparseArr[i][1];
sparseArr1[q][2] = sparseArr[i][2];
cpot[col]++;//当在三元组a中在同一列再次访问不同的数据时,该列访问的上一个元素的位置+1,表示在三元组b的存储位置上紧挨上一个与自己同列的数值,在该列继续向下存储数据
//指针对矩阵a中每列有多个非零数值,当该列只有一个非零数值时,该表达式不起任何效果,因为不会访问到该列的下一个非零数值
}
for (int i = 0; i < count; i++) {
System.out.println(sparseArr1[i][0] + " " + sparseArr1[i][1] + " " + sparseArr1[i][2]);
}
chessArr1=new int[col][row];
for (int i = 0; i < sparseArr1.length; i++) {
chessArr1[sparseArr1[i][0]][sparseArr1[i][1]] = sparseArr1[i][2];
}
System.out.println("转置后的稀疏矩阵:");
for(int[] col: chessArr1) {
for(int data:col) {
System.out.printf("%d\t",data);
}
System.out.println();
}
}
}
public class trsMatrix2 {
public static void main(String[] args) {
TcrMatrix1 t=new TcrMatrix1(3,5,6);
System.out.println("输入稀疏矩阵的三元组表 a :");
t.input();
System.out.println("输出稀疏矩阵的三元组表:");
t.display();
System.out.println("根据给出的三元组表还原稀疏矩阵:");
t.chessArr();
System.out.println("转置对应的三元组表 b :");
t.FastTranposition();
}
}
程序运行结果 文章来源地址https://www.toymoban.com/news/detail-778693.html
文章来源地址https://www.toymoban.com/news/detail-778693.html
到了这里,关于数据结构——稀疏矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!