简单说就是：拒绝域与备择假设方向相同。假设检验就是一个证伪的过程，原假设和备择假设是一对"相反的结论"。"拒绝域"，顾名思义，就是拒绝原假设的范围和方向，所以判断拒绝域在哪，可以直接看备择假设H1的条件是大于还是小于即可。
上述只是判断方法之一，但如果你能明白置信区间原理，自然就可以明白单侧假设检验的位置了。
从置信区间角度讲：例如，某个糖果厂宣称自家糖果的平均重量
-
方法1：平均重量是6.5
-
方法2：平均重量在[6.5-误差，6.5+误差]之间，置信度为0.95
方法1是一种点估计方法，只给出了一个近似值，但没有给出这个近似值的范围和置信度，因此方法1的结果相对方法2并不可靠。
双侧、单侧检验其实就考虑了这样的方法。
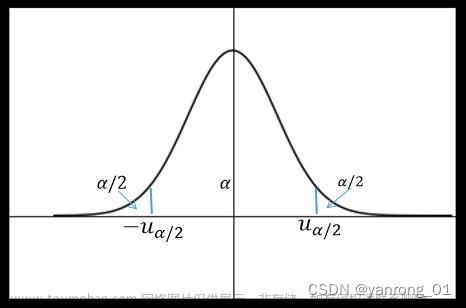
一、对于双侧检验，拒绝域有两种(两个方向)：
因为双侧检验的原假设H0：μ=6.5，H0的接受域是其两侧->[6.5-e，6.5+e]，e表示误差，而拒绝域是其接受域的"补集"。若拒绝域的面积(概率)为0.05，则接受域即置信区间[6.5-e，6.5+e]的置信度(面积、概率)为0.95。
二、单侧检验，拒绝域只有一种：
因为单侧检验的H0的符号一般是≥或≤，相应的H0的接受域、拒绝域如下
1、H0：μ≥6.5，
接受域位于6.5-e的左侧[6.5-e,+∞]，为左侧检验，检验“6.5-e”即统计量是否落在指定置信水平的拒绝域内
2、H0：μ≤6.5，
接受域位于6.5+e的右侧[-∞,6.5+e] ,为右侧检验，检验“6.5+e”即统计量是否落在指定置信水平的拒绝域内
而是否接受原假设，则可以通过判断统计量(“6.5±e”)是否落在拒绝域内，来判断是否接受原假设。而统计量的位置也可以通过概率来判断：
-
若统计量落在指定置信水平(比如α=0.05)的拒绝域内，则其接受域的面积必然大于1-α，
-
若统计量没有落在指定置信水平(比如α=0.05)的拒绝域内，则其接受域的面积必然小于1-α，
例子：JMP统计分析软件查看单侧检验结果
双侧检验：
H0：μ=6.5 H1：μ≠6.5
检验结果： ，|t |落在接受域内，接受原假设，可认为总体均值等于6.5。
右侧检验：
H0：μ≤6.5 ，H1：μ>6.5
检测结果：，t落在右侧拒绝域内，即拒绝原假设，认为总体均值大于样本均值6.5。
左侧T检验：
H0：μ≥6.5， H1：μ<6.5
检测结果： ，t 落在接受域内，即接受原假设，认为总体均值大于样本均值6.5。
文章来源：https://www.toymoban.com/news/detail-778828.html
注意，严格讲，假设检验就没有接受原假设这种说法，即假设检验结果只有拒绝原假设或不能拒绝原假设。假设检验就是一个证伪过程，尝试用反证法能否推翻(拒绝)原假设，反证成功(P值小于显著水平，即原假设是小概率事件)，则说明能拒绝原假设，反之(P大于显著水平)，只能说明反证失败，不能拒绝原假设，P大于显著水平，既不能拒绝也不能接受原假设，总之，只有P小于显著水平时假设检验才有统计意义。理论上是这样，但在很多实际应用中，例如许多统计分析软件(spss)，在解释正态性检验中，认为P值大于显著水平时，则接受原假设，数据服从正态分布。很矛盾......文章来源地址https://www.toymoban.com/news/detail-778828.html
到了这里，关于假设检验：如何理解单侧、双侧检验的拒绝域的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
