目录
一、实验目的:
二、内容:
1. 桥的定义
2. 求解问题
3. 算法
三、实验要求
四、实验内容和结果
基准算法
算法思想
伪代码
时间复杂度分析
算法效率测试
并查集
算法思想
伪代码
时间复杂度分析
算法效率测试
并查集(树)
算法思想
伪代码
时间复杂度分析
算法效率测试
路径压缩
算法思想
伪代码
时间复杂度分析
算法效率分析
启发式合并
算法思想
伪代码
时间复杂度分析
算法效率分析
最近公共祖先
算法思想
伪代码
时间复杂度分析
算法效率分析
五、实验总结
一、实验目的:
- 掌握图的连通性。
- 掌握并查集的基本原理和应用。
二、内容:
1. 桥的定义
在图论中,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。


图 1 没有桥的无向连通图 图 2 这是有16个顶点和6个桥的图(桥以红色线段标示)
2. 求解问题
找出一个无向图中所有的桥。
3. 算法
(1)基准算法
For every edge (u, v), do following
a) Remove (u, v) from graph
b) See if the graph remains connected (We can either use BFS or DFS)
c) Add (u, v) back to the graph.
(2)应用并查集设计一个比基准算法更高效的算法。不要使用Tarjan算法。
三、实验要求
- 实现上述基准算法。
- 设计的高效算法中必须使用并查集,如有需要,可以配合使用其他任何数据结构。
- 用图2的例子验证算法正确性。
- 使用文件 mediumG.txt和largeG.txt 中的无向图测试基准算法和高效算法的性能,记录两个算法的运行时间。
- 设计的高效算法的运行时间作为评分标准之一。
- 提交程序源代码。
- 实验报告中要详细描述算法设计的思想,核心步骤,使用的数据结构。
四、实验内容和结果
基准算法
算法思想
桥的判定与查找
由定义可知,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。那么很容易想到可以遍历边集,依次删除每一条边,如果连通块数量增加则代表这条边是“桥”。
图的连通块的计算
为了计算图的连通块,可以使用深度优先遍历(DFS)或广度优先遍历(BFS)这两种方式遍历整个图,在本实验中使用深度优先遍历(DFS)的方法计算连通块的数量。
算法流程
首先对初始的整张图使用DFS获取整张图的连通块数量count1,然后遍历边集,对于每条边ei都先将其从边集中移除,移除后再调用一次DFS获取此时图中的连通块数量count2,将ei添加回边集中,判断此时的count2是否大于count1,如果是,则本次遍历的边ei是桥。
流程图如下:

伪代码
brutalForce(graph) {
count1 = DFS(graph)
bridges = 0
for e in edges
delete e from edges
count2 = DFS(graph)
if count2 > count1
bridges++
add e to graphs
return bridges
}时间复杂度分析
设图中顶点数为n,边数为e。使用邻接表存储时,每个节点最多被遍历一次,所以每个节点最多调用一次DFS,这里的时间复杂度为O(n)。遍历图的实质是遍历每个节点的邻接节点,对于每个节点来说,遍历其邻接节点的时间复杂度为O(ei),这里的ei是第i个节点与其相邻节点所连的边的数量。所以遍历整个图的时候相当于遍历了所有节点和所有边,时间复杂度为O(n+e)。在此处进行了e次DFS,因此时间复杂度为O(ne+e²)。
对于稀疏图,有e∝n,此时的时间复杂度为O(n²);对于稠密图,有e∝n²,此时的时间复杂度为O()。
算法效率测试
算法正确性验证

利用本图进行算法正确性的验证,上图中有16个节点和15条边,将16个节点按从左到右、从上到下的顺序标号为0-15进行测试。
测试结果如下:

算法正确性得证。(在以下的算法中都验证了算法的正确性,不再一一列举)
算法效率分析
对三个不同规模的图进行测试
| 图2 | medium | large | |
| 运行时间/s | 0.0052 | 0.0283 | 栈溢出 |
| 桥数量 | 6 | 0 | 未知 |
在基准算法下,在规模较小和中等的图中有较快的运行效率,而在数据量很大的图中会由于栈溢出导致无法计算出结果。
并查集
算法思想
引入并查集
并查集是一种用于管理元素所属集合的数据结构,在本实验中,可以将每个连通块表示成一个集合,连通块中的节点表示为集合中的元素,采用一个数组来存储每个节点的所属连通块。
顾名思义,并查集支持两种操作:
- 合并(Union):合并两个节点所属连通块。
- 查询(Find):查询某个节点所属连通块,这可以用于判断两个节点是否属于同一连通块。
初始化
假设现在图中有10个互不相连的顶点,则此时应该有10个连通块,每个节点自成一个连通块。

由于在存储数组中的每个节点对应的值是所属连通块的代表节点,每个连通块的代表节点是连通块内随机一个节点的值,而初始情况下每个节点自成一个连通块,则初始情况下的存储数组应该为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
合并
首先合并节点3和节点4,此时在图中增加边的同时也需要更新数组中的值,由于合并后两节点属于同一个连通块,那么需要将原先其中一个连通块内所有节点在数组中的值更改为另一个连通块的代表节点。

此时的id数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 3 | 8 | 5 | 6 | 7 | 8 | 9 |
合并节点3和节点8,同理将其中一个连通块中所有节点在数组中的值改为另一个连通块中的代表节点。

此时的id数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 3 | 3 | 5 | 6 | 7 | 8 | 9 |
根据上述方法进行合并操作,最终结果如下所示。其中节点0,5,6,1,2,7属于同一个连通块,该连通块的代表节点为0;节点8,3,4,9属于同一个连通块,该连通块的代表节点为8。

在数组中的储存形式如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 1 | 1 | 1 | 8 | 8 | 1 | 1 | 1 | 8 | 8 |
查询
如果需要查找某个节点的所属连通块,只需要直接返回其在数组中的代表节点即可。
如果需要判断两个节点是否连通,只需要在数组中查找两个节点的代表节点是否相等即可。
例如在上图中,判断节点6和节点8是否连通,在数组中id[6] = 1,id[8] = 8,id[6] != id[8],因此两节点不连通。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 1 | 1 | 1 | 8 | 8 | 1 | 1 | 1 | 8 | 8 |
伪代码
Initial(id[]) {
for i in nodes
id[i] = i
}
Union(p, q) {
pid = id[p]
qid = id[q]
for i in nodes
if id[i] == pid
id[i] = qid
}
Find(p) {
return id[p]
}时间复杂度分析
设节点数为N
- 初始化:由于需要初始化数组为节点的值,所以时间复杂度为O(N)。
- 合并:由于需要遍历数组更改所有符合条件节点的代表节点,因此时间复杂度为O(N)。
- 查询:只需要在数组中返回节点下标对应的值即可,时间复杂度为O(1)。
算法效率测试
对三个不同规模的图进行测试
| 图2 | medium | large | |
| 基准算法/s | 0.0052 | 0.0283 | 栈溢出 |
| 并查集/s | 0.0101 | 0.9022 | 栈溢出 |
| 桥数量 | 6 | 0 | 未知 |
由于在判断一条边是否为桥的过程中,采用的方法是创建一个新的图(该图中的边数比原图中少一条),比较其连通分量数与原图的连通分量数的大小从而进行判断。
例如对边(0,1)进行判断即为以下情况

那么这种方法需要使用两层循环,外层循环遍历边集对每一条边进行判断,内层循环对新图进行边的增加。此时两层循环的时间花费是很昂贵的,因此在图的规模较小或者中等时该算法的时间效率反而低于基准算法。
并查集(树)
算法思想
将并查集实现为一个森林,其中每棵树表示一个连通块,树中的节点表示对应连通块中的节点。在存储数组中,节点下标对应的值不再是所属连通块中的代表节点,而是该节点的父节点。
初始化
以上个方法中的图为例,初始状态下的图及存储数组如下所示。此时每个节点自成一个连通块。

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
合并
合并节点3和节点4,采用树的结构,将节点4所属的连通块作为子节点连到节点3下。

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 3 | 3 | 5 | 6 | 7 | 8 | 9 |
合并节点3和节点8,此时节点3所属的树中不止一个节点,那么将节点3所属的树作为子树接入到节点8下。在存储数组中的表示为将一棵子树的根节点对应的值改为另一棵子树的根节点。

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 8 | 3 | 5 | 6 | 7 | 8 | 9 |
合并节点8和节点9,此时可以将节点9作为子节点接入节点8所属的树中。

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 2 | 8 | 3 | 5 | 6 | 7 | 8 | 8 |
经过一系列的合并操作,最终得到的森林如下所示

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 1 | 8 | 1 | 8 | 3 | 0 | 5 | 1 | 8 | 8 |
可以看到数组中每个节点下标对应存储的值都是它的父节点,根节点对应存储的值是它本身。
查询
由于每个连通分量被表示为一棵树,每棵树的代表节点是它的根节点,如果需要查找一个节点所属的连通块,那么只需要自底向上不断查找它的父节点直到根节点即可。
如果需要判断两个节点间是否连通,只需要分别找到它们所属子树的根节点判断是否相等即可。
例如在下图中,判断节点3和节点5是否在同一个连通块中,从节点3向上寻找,它的根节点是9;从节点5向上寻找,它的根节点是6,因此不属于同一连通块。

对应的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| id[] | 0 | 1 | 9 | 4 | 9 | 6 | 6 | 7 | 8 | 9 |
伪代码
Initial(id[]) {
for i in nodes
id[i] = i
}
find(p) {
while p != id[p]
p = id[p]
return p
}
union(p, q) {
proot = find[p]
qroot = find[q]
id[proot] = qroot
}时间复杂度分析
设节点数为N
- 初始化:初始化需要遍历所有节点,时间复杂度为O(N)。
- 查询:查询一个节点需要自底向上寻找到根节点,在最坏情况下需要遍历所有节点,因此时间复杂度为O(N)。
- 合并:合并操作也需要先查询两个节点的根节点,时间复杂度为O(N)。
算法效率测试
对三个不同规模的图进行测试
| 图2 | medium | large | |
| 基准算法/s | 0.0052 | 0.0283 | 栈溢出 |
| 并查集/s | 0.0101 | 0.9022 | 栈溢出 |
| 并查集(树)/s | 0.0032 | 0.0308 | 栈溢出 |
| 桥数量 | 6 | 0 | 未知 |
此时对并查集采用树形的存储相较于用一个节点代表一个集合的并查集而言,效率得到了显著的提升。
路径压缩
算法思想
在上述并查集中,要想找到一棵树的代表元素,那么需要沿着节点的父节点自底向上地去寻找它的根节点,很显然当树很高的时候,逐层向上查找的方式是非常耗费时间的。
由于我们的目的只是找到节点所在树的根节点,所以我们并不关心往上寻找的路径上经过的节点。因此可以在计算完树的根节点后,将每个已检查节点的id值改为所在树的根节点。这种做法可以使每个节点到根节点的路径长度大大减小,提高了后续查找的效率。
例如在以下树中,要找到节点9的代表元素,在未压缩路径时需要经过的路径为9-6-3-1-0,才能最终找到根节点。

当前初始情况下的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| id[] | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 3 | 6 | 6 | 8 | 9 | 9 |
如果采用路径压缩的方法,在查找的过程中,自底向上地将路径上所有节点的前驱都改为根节点。首先将节点9的前驱改为根节点

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| id[] | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 3 | 6 | 0 | 8 | 9 | 9 |
将路径上的下一个节点6连到根节点处

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| id[] | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 3 | 6 | 0 | 8 | 9 | 9 |
将路径上的下一个节点3连到根结点处

此时的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| id[] | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 3 | 6 | 0 | 8 | 9 | 9 |
由于节点1的前驱结点就是根节点,因此不需要再进行改变,最终经过路径压缩后的图如下所示

最终的存储数组为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| id[] | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 3 | 6 | 0 | 8 | 9 | 9 |
此时由于更新了存储数组,因此在后续的查找中,就可以直接在id数组中找到根节点,避免了重复无效的工作。
伪代码
pathCompressionFind(p) { //由于子节点的代表节点就是根节点 因此从孙子节点开始进行压缩
while p != id[p]
id[p] = id[id[p]] //边寻找边压缩
p = id[p]
return p
}时间复杂度分析
设一共有N个节点,在压缩路径过程中,递归向上改变路径上的每个节点在存储数组中的值,在最坏的情况下需要遍历所有的节点,时间复杂度为O(N)。
算法效率分析
对三个不同规模的图进行测试
| 图2 | medium | large | |
| 基准算法/s | 0.0052 | 0.0283 | 栈溢出 |
| 并查集/s | 0.0101 | 0.9022 | 栈溢出 |
| 并查集(树)/s | 0.0032 | 0.0308 | 栈溢出 |
| 并查集+路径压缩/s | 0.0034 | 0.0276 | 栈溢出 |
| 桥数量 | 6 | 0 | 未知 |
启发式合并
算法思想
假设现在要对节点7和节点3所在树进行合并操作,两树如下所示

此时有两种选择:将左树作为子树接入右树中,或者将右树作为子树接入左树中。

为提高效率,我们应该使树尽可能地矮一些,因此我们应该改变随机连接的方式,而是总是将较矮的树接到较高的树下,也就是说在上述情况中,应该选择第一种连接方式。
为了实现这种连接方式,需要增加一个数组对每个节点的高度进行存储,则每棵树的高度就是该树的根节点在数组中存储的高度。
伪代码
weightedUnion(p, q) {
proot = find(p) //寻找p所在树的根节点
qroot = find(q) //寻找q所在树的根节点
if proot == qroot //如果在同一树中 不进行合并操作
return
if height[proot] < height[qroot] //如果p较矮 则p作为子树连到q树下
id[proot] = qroot
else if height[proot] > height[qroot] //如果q较矮 则q作为子树连到p树下
id[qroot] = proot
else //如果两树高度相等 随意连接 并将连接后的树高度加一
id[proot] = qroot
height[qroot] + 1
}时间复杂度分析
设节点数为N,本算法的时间复杂度主要来自寻找根节点,根据启发式合并的原则,树的高度不会超过logN,因此在寻找过程中只需要向上寻找最多logN - 1次。由于合并的时间复杂度主要来源于查询,因此利用该算法可以使合并和查询操作的时间复杂度都为O(logN)。

算法效率分析
对三个不同规模的图进行测试
| 图2 | medium | large | |
| 基准算法/s | 0.0052 | 0.0283 | 栈溢出 |
| 并查集/s | 0.0101 | 0.9022 | 栈溢出 |
| 并查集(树)/s | 0.0032 | 0.0308 | 栈溢出 |
| 并查集+路径压缩/s | 0.0034 | 0.0276 | 栈溢出 |
| 并查集+路径压缩+启发式合并/s | 0.0039 | 0.0208 | 栈溢出 |
| 桥数量 | 6 | 0 | 未知 |
至此已经采用了并查集+路径压缩+启发式合并的优化算法,但是依然由于内存问题导致无法进行大规模数据的运算,因此还需要再对算法进行优化。
最近公共祖先
算法思想
在前面的算法中,每次对桥的查找都需要去掉一条边,然后根据连通变量数目的变化进行判断。而当边的数目过多时,利用这种方法来统计桥的数目需要的时间开销是很大的。
因此可以转换思路,排除所有不是桥的边,剩下的都是桥。根据定理:如果边e是图G的割边,当且仅当e不在G的任意一个环中。因此需要去掉图中所有的环、平行边,剩下的就是桥。
并查集
当使用并查集进行合并操作时,如果发现需要合并的两个节点x和y已经在一个连通分量内了,则说明边(x,y)是一条环边。此时不需要将这条边加入图中,但是需要将其记录下来。
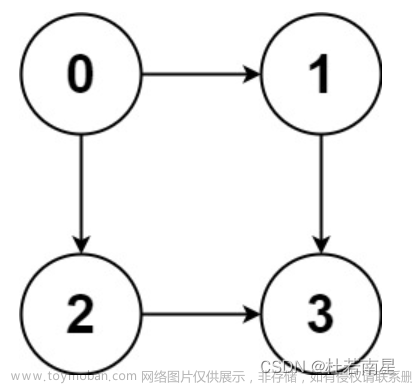
以题目中的图2为例进行说明,按照顺序对每条边进行判断是否需要加入图中。

首先将各节点初始化如下,并按顺序进行标号

首先连接节点0和节点1。两节点不在一个连通分量中,将两节点合并,并添加边到图中。

连接节点2和节点3。同样不在同一连通分量中,将两节点合并并添加边。

依次将(2,6)(6,7)(4,8)(4,9)加入图中,原因同上。

此时需要加入边(8,9),发现节点8和9已经在同一连通分量中,因此不进行合并和加边操作,但是记录边(8,9)为环边。

加入边(8,13)

对于边(9,13),记录但不加入,理由同上。

加入边(12,13)(9,10)(10,11)(10,14)(11,15)

对于边(14,15),记录但不加入。

最近公共祖先
在一棵没有环的树上,除根节点外每个节点都有其父节点和祖先节点,最近公共祖先就是两个节点在这棵树上深度最大的公共祖先节点。寻找两个节点的最近公共节点即根据两个节点的深度分别向树根方向查找,当查找到第一个相同节点时,该节点即为两个节点的最近公共祖先。
例如在上面的例子中,节点13和9的最近公共祖先为4。

接下来依次取出存储的环边,寻找每条环边中两节点的最近公共祖先,这样就能找到图中每个环。在每组节点向上查找最近公共祖先的路径上的边也是所在环中的环边。由此可以找到所有环边,进而得到桥。
依次寻找节点8和9,9和13,14和15的最近公共祖先,其中节点8和9,9和13的最近公共祖先都是4,14和15的最近公共祖先为10。将寻找路径上的边都记录为环边。

此时减去图中标记出的环边,剩余的边就都是桥了。

伪代码
并查集
Union(Graph) // 在将每条边加入图中之前先对其进行判断
for edge in edges
v1 = edge.v1
v2 = edge.v2
root1 = find(v1)
root2 = find(v2)
if root1 == root2
note edge as a cycle edge
else
weightedUnion(v1, v2)最近公共祖先
由于在寻找两节点的最近公共祖先时,有可能出现两节点所处在树中的深度不同的情况,此时如果同时向上查找会出现永远无法相交的情况,因此需要进行降深度的操作,在初始化时用depth数组对每个节点的深度进行存储。容易想到,在降深度的过程中所经过的边也应标记为环边。
DFS(root, depth)
visited[root] = true
root.depth = depth
for i in vnum
if adj[root][i] == 1 and visited[i] == false
DFS(root, depth + 1)
Initial(Graph)
for i in vnum
if id[i] == i
DFS(i, 0)再引入一个布尔型的数组isBridge对每条边是否为桥进行存储。由于除根节点外的每个节点都有唯一的一个父节点,因此可以用数组中的每个元素表示一条对应的边(下标对应节点,该节点的父节点),以上图为例,边(9,10)为桥,则isBridge[9] 代表边(9,10),值为true。
LCA(Graph)
//因为是排除不是桥的边,所以初始化所有边为桥。标记根节点都为环边,因为根节点不存在父节点。
for i in vnum
isBridge[i] = true
if id[i] == i
isBridge[i] = false
//遍历记录下来的每条环边,进行降深度操作,并将降深度路径上的边标记为环边
for edge in circleEdges
if depth[edge.v1] != depth[edge.v2]
while depth[edge.v1] > depth[edge.v2]
isBridge[edge.v1] = false
edge.v1 = edge.v1.father
while depth[edge.v1] < depth[edge.v2]
isBridge[edge.v2] = false
edge.v2 = edge.v2.father
//寻找最近公共祖先并将路径上的边标记为环边
else
while edge.v1 != edge.v2
isBridge[edge.v1] = false
isBridge[edge.v2] = false
edge.v1 = edge.v1.father
edge.v2 = edge.v2.father时间复杂度分析
设顶点数为N,边数为E。
- 并查集:对边进行遍历的时间复杂度为O(E)。由于使用启发式合并,由上面的分析可知查找和合并的时间复杂度都为O(logN)。
- 最近公共祖先:遍历节点的时间复杂度为O(N),向上寻找的时间复杂度也是O(logN)。
算法效率分析
对三个不同规模的图进行测试
| 图2 | medium | large | |
| 基准算法/s | 0.0052 | 0.0283 | 栈溢出 |
| 并查集/s | 0.0101 | 0.9022 | 栈溢出 |
| 并查集(树)/s | 0.0032 | 0.0308 | 栈溢出 |
| 并查集+路径压缩/s | 0.0034 | 0.0276 | 栈溢出 |
| 并查集+路径压缩+启发式合并/s | 0.0039 | 0.0208 | 栈溢出 |
| 并查集+LCA/s | 0.0051 | 0.0002 | 5.3832 |
| 桥数量 | 6 | 0 | 8 |
使用此算法终于计算出了大规模下图中桥的数量,并且达到了较高的运行效率。对于中等规模的数据而言,运行时间几乎可以忽略不计。文章来源:https://www.toymoban.com/news/detail-778865.html
五、实验总结
在本次实验中,首先使用基准算法进行测试,对本次的实验有了一个大概的认识并在小规模数据和中等规模的数据下都有不错的运行效率,但是无法对大规模数据进行求解。而在引入了并查集、路径压缩和启发式合并的优化算法之后,依然无法在大规模数据下求解出结果,因此采用逆向思维,引入最近公共祖先利用去除环边的方式求得桥,从而成功求解出了大规模数据下的桥的数量。文章来源地址https://www.toymoban.com/news/detail-778865.html
到了这里,关于【算法设计与分析】图论(桥)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!