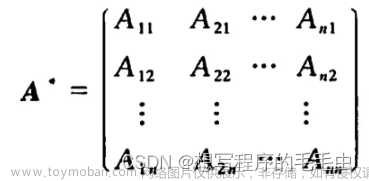
题目描述
上三角形矩阵是指主对角线以下(不包含主对角线)元素全为0的矩阵。
现输入一个数字n,显然该矩阵中含有n * n个元素, 若满足上三角矩阵, 则含有(n * n + n) / 2个非0元素。
请将1 ~ (n * n + n) / 2的数字按顺序填入该上三角矩阵。
顺序:先按行, 若行相同则按列。
输入
输入一个n(1 ≤ 100)代表该上三角形矩阵的大小。文章来源:https://www.toymoban.com/news/detail-779079.html
输出
输出n行, 每行n个元素。文章来源地址https://www.toymoban.com/news/detail-779079.html
#include <stdio.h>
int main(){
int n,a=1,b,c,d;
scanf("%d",&n);
for (int i = 0; i < n ; ++i) {
for (int j = 0; j < i ; ++j) {
printf("0 ");
}
for (int j = i; j < n ; ++j) {
printf("%d ",a);
a++;
}
printf("\n");
}
}到了这里,关于heanauOJ 1083: 超简单的构造上三角矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!