1. Toy模板网首页
  2. > Toy博客

图之最小生成树Prim算法详解(C语言版)

9月前 作者：红心火柴 分类：Toy博客 阅读(45) 违法举报

这篇具有很好参考价值的文章主要介绍了图之最小生成树Prim算法详解(C语言版)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、Prim算法思想

普里姆算法采用贪心算法的思想来查找最小生成树。对于包含 N 个顶点的连通网，普里姆算法每次从连通网中找出一个权值最小的边，这样的操作重复 N-1次，由N-1条权值最小的边组成的生成树就是最小生成树MST（Minimum Spanning Tree，最小生成树）。

那么，如何找出N-1条权值最小的边呢？普里姆算法的实现思路是：

  1. 将连通网中的所有顶点分为两类（假设为 A 类和 B 类）。初始状态下，所有顶点位于 B 类；
  2. 选择任意一个顶点，将其从 B 类移动到 A 类；
  3. 从 B 类的所有顶点出发，找出一条连接着 A 类中的某个顶点且权值最小的边，将此边连接着的 A 类中的顶点移动到 B 类；
  4. 重复执行第 3 步，直至 B 类中的所有顶点全部移动到 A 类，恰好可以找到 N-1 条边。

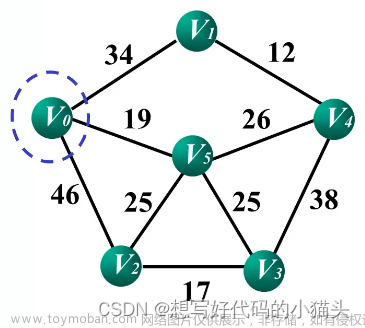
举个例子，下图是一个连通网有A、B、C、D、E、F六个顶点，它们的编号依次是0、1、2、3、4、5，使用普里姆算法查找最小生成树，需经历以下过程：
prim算法c语言,数据结构与算法,算法,c语言,图论
设置2个数据结构：
lowcost[i]:表示以 i 为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值等于0,也就是表示 i 点加入了MST
mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边(即<起点,终点>)，当mst[i]=-1表示起点 i 加入MST

我们假设顶点 A 是起始点，进行初始化（*代表无限大，即无通路）：

以i为终点的边的最小权值
lowcost[0]=0
lowcost[1]=6
lowcost[2]=1
lowcost[3]=5
lowcost[4]=*
lowcost[5]=*

对应lowcost[i]的起点(所有点默认起点是A)
mst[0]=-1
mst[1]=0
mst[2]=0
mst[3]=0
mst[4]=0
mst[5]=0

明显看出，以顶点 C 为终点的边的权值最小等于1，所以边<mst[2],2>=1加入MST（即lowcost[2]=0,mst[2]=-1）
prim算法c语言,数据结构与算法,算法,c语言,图论

此时，因为顶点 C 的加入，就能够获取到以顶点 C 为起点的边信息以及边相应终点的信息，需要更新lowcost数组和mst数组：

lowcost[0]=0
lowcost[1]=5
lowcost[2]=0
lowcost[3]=5
lowcost[4]=6
lowcost[5]=4
mst[0]=-1
mst[1]=2
mst[2]=-1
mst[3]=0
mst[4]=2
mst[5]=2

明显看出，以顶点 F 为终点的边的权值最小等于4，所以边<mst[5],5>=4加入MST（即lowcost[5]=0,mst[5]=-1）
prim算法c语言,数据结构与算法,算法,c语言,图论

此时，因为顶点 F 的加入，就能够获取到以顶点 F 为起点的边信息以及边相应终点的信息，需要更新lowcost数组和mst数组：

lowcost[0]=0
lowcost[1]=5
lowcost[2]=0
lowcost[3]=2
lowcost[4]=6
lowcost[5]=0
mst[0]=-1
mst[1]=2
mst[2]=-1
mst[3]=5
mst[4]=2
mst[5]=-1

明显看出，以顶点 D 为终点的边的权值最小等于2，所以边<mst[3],3>=2加入MST（即lowcost[3]=0,mst[3]=-1）
prim算法c语言,数据结构与算法,算法,c语言,图论

此时，因为顶点 D 的加入，就能够获取到以顶点 D 为起点的边信息以及边相应终点的信息，需要更新lowcost数组和mst数组：

lowcost[0]=0
lowcost[1]=5
lowcost[2]=0
lowcost[3]=0
lowcost[4]=6
lowcost[5]=0
mst[0]=-1
mst[1]=2
mst[2]=-1
mst[3]=-1
mst[4]=2
mst[5]=-1

明显看出，以顶点 B 为终点的边的权值最小等于5，所以边<mst[1],1>=5加入MST（即lowcost[1]=0,mst[1]=-1）
prim算法c语言,数据结构与算法,算法,c语言,图论
此时，因为顶点 B 的加入，就能够获取到以顶点 B 为起点的边信息以及边相应终点的信息，需要更新lowcost数组和mst数组：

lowcost[0]=0
lowcost[1]=0
lowcost[2]=0
lowcost[3]=0
lowcost[4]=3
lowcost[5]=0
mst[0]=-1
mst[1]=-1
mst[2]=-1
mst[3]=-1
mst[4]=1
mst[5]=-1

很明显，以顶点 E 为终点的边的权值最小等于3，所以边<mst[4],4>=3加入MST（即lowcost[4]=0,mst[4]=-1）

lowcost[0]=0
lowcost[1]=0
lowcost[2]=0
lowcost[3]=0
lowcost[4]=0
lowcost[5]=0
mst[0]=-1
mst[1]=-1
mst[2]=-1
mst[3]=-1
mst[4]=-1
mst[5]=-1

至此，MST构建成功,如下图所示：
prim算法c语言,数据结构与算法,算法,c语言,图论

二、数据结构

1、使用邻接矩阵存放图结构
对于邻接矩阵不是很了解的可以查看文章：图之邻接矩阵详解（C语言版）

//设置默认的顶点个数
#define Default_Vertex_Size  10
//数据类型
#define T char
#define E int
#define MAX_COST  0x7FFFFFFF //代表无穷大

//邻接矩阵图结构
typedef struct GraphMtx
{
	int MaxVertices; //最大顶点数
	int NumVertices; //真实的顶点数
	int NumEdges;  //边数

	T   *VerticesList; //顶点列表
	int **Edge; //边信息矩阵
}GraphMtx;

prim算法c语言,数据结构与算法,算法,c语言,图论

2、使用lowcost数组和mst数组辅助完成Prim算法

  • lowcost[i]:表示以 i 为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值等于0,也就是表示 i 点加入了MST
  • mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边(即<起点,终点>)，当mst[i]=0表示起点 i 加入MST，当mst[i]=-1表示起点 i 加入MST
int n = g->NumVertices; //获取图的顶点个数
//lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
E *lowcost = (E*)malloc(sizeof(E)*n); //lowcost[n] 
//mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边
int *mst = (int *)malloc(sizeof(int)*n);//mst[n]

三、代码实现

1、邻接矩阵实现

图初始化

//图的初始化
void InitGraph(GraphMtx *g)
{
	g->MaxVertices = Default_Vertex_Size;//最大顶点数初始化
	g->NumVertices = g->NumEdges = 0; //实际顶点数初始化

	//分配顶点存储列表的空间
	g->VerticesList = (T*)malloc(sizeof(T)*(g->MaxVertices));
	assert(g->VerticesList != NULL);

	//开辟边信息存储矩阵的空间（二维数组的动态开辟）
	g->Edge = (int**)malloc(sizeof(int*) * g->MaxVertices); //总行数的开辟
	assert(g->Edge != NULL);
	for(int i=0; i<g->MaxVertices; ++i) //每一行内具体的空间开辟
	{
		g->Edge[i] = (int*)malloc(sizeof(int) * g->MaxVertices);
	}
	for(i=0; i<g->MaxVertices; ++i)  //初始化
	{
		for(int j=0; j<g->MaxVertices; ++j)
		{
			if(i == j)
			{
				g->Edge[i][j] = 0;
			}
			else
			{
				g->Edge[i][j] = MAX_COST;
			}
		}
	}
}

获取顶点的位置

//获取顶点的位置
int  GetVertexPos(GraphMtx *g, T v)
{
	for(int i=0; i<g->NumVertices; ++i) //对所有顶点进行遍历
	{
		//判断是否找到顶点v所在位置
		if(g->VerticesList[i] == v)
			return i;
	}
	return -1;
}

打印图信息

//打印图信息
void ShowGraph(GraphMtx *g)
{
	printf("  ");
	for(int i=0; i<g->NumVertices; ++i) //获取顶点，并打印
	{
		printf("%c  ",g->VerticesList[i]);
	}
	printf("\n");
	for(i=0; i<g->NumVertices; ++i) //打印顶点间边的信息
	{
		printf("%c ",g->VerticesList[i]);
		for(int j=0; j<g->NumVertices; ++j)
		{
			if(g->Edge[i][j] == MAX_COST)
			{
				printf("%c  ",'@');
			}
			else
			{
				printf("%d  ",g->Edge[i][j]);
			}
		}
		printf("\n");
	}
	printf("\n");
}

插入顶点

//插入顶点
void InsertVertex(GraphMtx *g, T v)
{
	if(g->NumVertices >= g->MaxVertices) //判断顶点空间是否已满
		return;
	g->VerticesList[g->NumVertices++] = v; //还有空间，放入顶点
}

插入边：在v1和v2顶点间插入边

//插入边：在v1和v2顶点间插入边
void InsertEdge(GraphMtx *g, T v1, T v2, E cost)
{
	int p1 = GetVertexPos(g,v1);  //获取v1顶点位置
	int p2 =  GetVertexPos(g,v2);  //获取v2顶点位置
	if(p1==-1 || p2==-1)
		return;

	//无向图存储 需要双向的
	g->Edge[p1][p2] = g->Edge[p2][p1] = cost;
	g->NumEdges++; //记录实际边数
}

删除边：删除v1和v2顶点间的边

//删除边：删除v1和v2顶点间的边
void RemoveEdge(GraphMtx *g, T v1, T v2)
{
	//求出两个顶点的下标位置
	int p1 = GetVertexPos(g,v1);
	int p2 =  GetVertexPos(g,v2);
	if(p1==-1 || p2==-1)
		return;

	if(g->Edge[p1][p2] == 0)
		return;

	//将边清空
	g->Edge[p1][p2] = g->Edge[p2][1] = 0;
	g->NumEdges--; //更新边数
}

删除顶点

//删除顶点
void RemoveVertex(GraphMtx *g, T v)
{
	//获取顶点的位置
	int p = GetVertexPos(g,v);
	if(p == -1)
		return;

	
	//释放顶点
	int numedges = 0;

	for(int i=p; i<g->NumVertices-1; ++i)
	{
		//将要释放顶点之后的顶点逐一前移
		g->VerticesList[i] = g->VerticesList[i+1];
	}

	//统计与要删除顶点相连的边条数
	for(i=0; i<g->NumVertices; ++i)
	{
		if(g->Edge[p][i] != 0)
		{
			numedges++;
		}
	}

	//删除与释放顶点相连的边（更改存放边信息的矩阵）
	for(i=p; i<g->NumVertices-1; ++i)
	{
		//将要删除行之后的行逐一向前移动一行
		for(int j=0; j<g->NumVertices; ++j)
		{
			g->Edge[i][j] = g->Edge[i+1][j];
		}
	}

	for(i=p; i<g->NumVertices; ++i)//删除列
	{
		//将要删除列之后的列逐一向前移动一列
		for(int j=0; j<g->NumVertices; ++j)
		{
			g->Edge[j][i] = g->Edge[j][i+1];
		}
	}
	g->NumVertices--;
	g->NumEdges -= numedges;
}

销毁图

//销毁图
void DestroyGraph(GraphMtx *g)
{
	//释放顶点
	free(g->VerticesList);
	g->VerticesList = NULL;
	//释放边存储结构的列
	for(int i=0; i<g->NumVertices; ++i)
	{
		free(g->Edge[i]);
	}
	free(g->Edge);//释放存放行指针的空间
	g->Edge = NULL;
	g->MaxVertices = g->NumEdges = g->NumVertices = 0;
}

获取v第一个邻接顶点

//获取v第一个邻接顶点
int  GetFirstNeighbor(GraphMtx *g, T v)
{
	//获取顶点v所在位置
	int p = GetVertexPos(g,v);
	if(p == -1)
		return -1;

	//对顶点进行搜索，看那个顶点与v相连
	for(int i=0; i<g->NumVertices; ++i)
	{
		//判断是否，找到
		if(g->Edge[p][i] == 1)
			return i; //找到即返回
	}
	return -1;
}

获取下一个邻接顶点：获取顶点v的邻接顶点（该邻接点的顺序在邻接点w之后）

//获取下一个邻接顶点：获取顶点v的邻接顶点（该邻接点的顺序在邻接点w之后）
int  GetNextNeighbor(GraphMtx *g, T v, T w)
{
	//获取v和w所在位置
	int pv = GetVertexPos(g,v);
	int pw = GetVertexPos(g,w);
	if(pv==-1 || pw==-1)
		return -1;

	//从v的邻接顶点w的位置向后搜索，找到第一个与v相邻的顶点，即所求
	for(int i=pw+1; i<g->NumVertices; ++i)
	{
		
		if(g->Edge[pv][i] == 1)
			return i; 
	}
	return -1;
}

获取边的权重

//获取边的权重
E    GetWeight(GraphMtx *g, int v1, int v2)
{
	if(v1==-1 || v2==-1)
		return MAX_COST;
	return g->Edge[v1][v2];
}

2、Prim算法实现

//通过Prim算法获取最小生成树，其中g为邻接矩阵表示的图，vertex为生成树的起点
void MinSpanTree_Prim(GraphMtx *g, T vertex)
{
	int n = g->NumVertices; //获取图的顶点个数
	//lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
	E *lowcost = (E*)malloc(sizeof(E)*n); //lowcost[n] 
	//mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=-1表示起点 i 加入MST
	int *mst = (int *)malloc(sizeof(int)*n);//mst[n]
	assert(lowcost!=NULL && mst!=NULL);

	//初始化lowcost和mst
	int k = GetVertexPos(g,vertex);//获取顶点的位置
	for(int i=0; i<n; ++i)
	{
		if(i != k)
		{
			
			lowcost[i] = GetWeight(g,k,i); //保存边值	
			mst[i] = k; //保存顶点
		}
		else
		{
			lowcost[i] = 0; //保存边值,表示i点加入了MST
			mst[i] = -1; //保存顶点,表示i点加入了MST
		}
	}

	int min,min_index;
	int begin,end;
	E cost;

	for(i=0; i<n-1; ++i)
	{
		min = MAX_COST;
		min_index = -1;
		//寻找最小的花费代价，并且记录对应的终止顶点
		for(int j=0; j<n; ++j)
		{
			
			if(lowcost[j]!=0 && lowcost[j]<min)
			{//顶点未加入到数组中且边的权值小于最小值			
				min = lowcost[j];
				min_index = j;
			}
		}
		//获取查找到的权值最小边的起始位置和终止位置
		begin = mst[min_index]; //起始顶点位置
		end = min_index; //终止顶点位置
		printf("%c-->%c : %d\n",g->VerticesList[begin],g->VerticesList[end],min);//最小生成树的顶点和边
		//将找到权值最小边的终止顶点标记为已经处理
		lowcost[min_index] = 0;
		mst[min_index] = -1;

		//查询与新加入的顶点相连接的边是否有存在更短的，有的话就需要进行记录
		for(j=0; j<n; ++j)
		{
			cost = GetWeight(g,min_index,j);
			if(cost < lowcost[j])
			{
				lowcost[j] = cost;
				mst[j] = min_index;
			}
		}
	}
}

3、运行结果

#include"GraphMtx.h"

void main()
{
	//使用邻接矩阵来存放图结构
	GraphMtx gm;
	InitGraph(&gm);
	//插入图结点
	InsertVertex(&gm,'A');
	InsertVertex(&gm,'B');
	InsertVertex(&gm,'C');
	InsertVertex(&gm,'D');
	InsertVertex(&gm,'E');
	InsertVertex(&gm,'F');
	//插入边
	InsertEdge(&gm,'A','B',6);
	InsertEdge(&gm,'A','C',1);
	InsertEdge(&gm,'A','D',5);
	InsertEdge(&gm,'B','C',5);
	InsertEdge(&gm,'B','E',3);
	InsertEdge(&gm,'C','D',5);
	InsertEdge(&gm,'C','E',6);
	InsertEdge(&gm,'C','F',4);
	InsertEdge(&gm,'D','F',2);
	InsertEdge(&gm,'E','F',6);
	ShowGraph(&gm);
	//获取以'E'为起点的最小生成树
	MinSpanTree_Prim(&gm,'E');
}

运行结果
prim算法c语言,数据结构与算法,算法,c语言,图论

测试的图结构
prim算法c语言,数据结构与算法,算法,c语言,图论

获取的最小生成树
prim算法c语言,数据结构与算法,算法,c语言,图论

附录

测试代码

Main.cpp

#include"GraphMtx.h"

void main()
{
	//使用邻接矩阵来存放图结构
	GraphMtx gm;
	InitGraph(&gm);
	//插入图结点
	InsertVertex(&gm,'A');
	InsertVertex(&gm,'B');
	InsertVertex(&gm,'C');
	InsertVertex(&gm,'D');
	InsertVertex(&gm,'E');
	InsertVertex(&gm,'F');
	//插入边
	InsertEdge(&gm,'A','B',6);
	InsertEdge(&gm,'A','C',1);
	InsertEdge(&gm,'A','D',5);
	InsertEdge(&gm,'B','C',5);
	InsertEdge(&gm,'B','E',3);
	InsertEdge(&gm,'C','D',5);
	InsertEdge(&gm,'C','E',6);
	InsertEdge(&gm,'C','F',4);
	InsertEdge(&gm,'D','F',2);
	InsertEdge(&gm,'E','F',6);
	ShowGraph(&gm);
	//获取以'E'为起点的最小生成树
	MinSpanTree_Prim(&gm,'E');
}

GraphMtx.h

#pragma once
#include<stdio.h>
#include<malloc.h>
#include<assert.h>

//设置默认的顶点个数
#define Default_Vertex_Size  10
//数据类型
#define T char
#define E int
#define MAX_COST  0x7FFFFFFF //代表无穷大

//邻接矩阵图结构
typedef struct GraphMtx
{
	int MaxVertices; //最大顶点数
	int NumVertices; //真实的顶点数
	int NumEdges;  //边数

	T   *VerticesList; //顶点列表
	int **Edge; //边信息矩阵
}GraphMtx;

void InitGraph(GraphMtx *g);
int  GetVertexPos(GraphMtx *g, T v);
void ShowGraph(GraphMtx *g);
void InsertVertex(GraphMtx *g, T v);
void InsertEdge(GraphMtx *g, T v1, T v2, E cost);
void RemoveVertex(GraphMtx *g, T v);
void RemoveEdge(GraphMtx *g, T v1, T v2);
void DestroyGraph(GraphMtx *g);
int  GetFirstNeighbor(GraphMtx *g, T v);
int  GetNextNeighbor(GraphMtx *g, T v, T w);

E    GetWeight(GraphMtx *g, int v1, int v2);
void MinSpanTree_Prim(GraphMtx *g, T vertex);

GraphMtx.cpp文章来源地址https://www.toymoban.com/news/detail-779197.html

#include"GraphMtx.h"

//图的初始化
void InitGraph(GraphMtx *g)
{
	g->MaxVertices = Default_Vertex_Size;//最大顶点数初始化
	g->NumVertices = g->NumEdges = 0; //实际顶点数初始化

	//分配顶点存储列表的空间
	g->VerticesList = (T*)malloc(sizeof(T)*(g->MaxVertices));
	assert(g->VerticesList != NULL);

	//开辟边信息存储矩阵的空间（二维数组的动态开辟）
	g->Edge = (int**)malloc(sizeof(int*) * g->MaxVertices); //总行数的开辟
	assert(g->Edge != NULL);
	for(int i=0; i<g->MaxVertices; ++i) //每一行内具体的空间开辟
	{
		g->Edge[i] = (int*)malloc(sizeof(int) * g->MaxVertices);
	}
	for(i=0; i<g->MaxVertices; ++i)  //初始化
	{
		for(int j=0; j<g->MaxVertices; ++j)
		{
			if(i == j)
			{
				g->Edge[i][j] = 0;
			}
			else
			{
				g->Edge[i][j] = MAX_COST;
			}
		}
	}
}

//获取顶点的位置
int  GetVertexPos(GraphMtx *g, T v)
{
	for(int i=0; i<g->NumVertices; ++i) //对所有顶点进行遍历
	{
		//判断是否找到顶点v所在位置
		if(g->VerticesList[i] == v)
			return i;
	}
	return -1;
}

//打印图信息
void ShowGraph(GraphMtx *g)
{
	printf("  ");
	for(int i=0; i<g->NumVertices; ++i) //获取顶点，并打印
	{
		printf("%c  ",g->VerticesList[i]);
	}
	printf("\n");
	for(i=0; i<g->NumVertices; ++i) //打印顶点间边的信息
	{
		printf("%c ",g->VerticesList[i]);
		for(int j=0; j<g->NumVertices; ++j)
		{
			if(g->Edge[i][j] == MAX_COST)
			{
				printf("%c  ",'@');
			}
			else
			{
				printf("%d  ",g->Edge[i][j]);
			}
		}
		printf("\n");
	}
	printf("\n");
}

//插入顶点
void InsertVertex(GraphMtx *g, T v)
{
	if(g->NumVertices >= g->MaxVertices) //判断顶点空间是否已满
		return;
	g->VerticesList[g->NumVertices++] = v; //还有空间，放入顶点
}

//插入边：在v1和v2顶点间插入边
void InsertEdge(GraphMtx *g, T v1, T v2, E cost)
{
	int p1 = GetVertexPos(g,v1);  //获取v1顶点位置
	int p2 =  GetVertexPos(g,v2);  //获取v2顶点位置
	if(p1==-1 || p2==-1)
		return;

	//无向图存储 需要双向的
	g->Edge[p1][p2] = g->Edge[p2][p1] = cost;
	g->NumEdges++; //记录实际边数
}

//删除边：删除v1和v2顶点间的边
void RemoveEdge(GraphMtx *g, T v1, T v2)
{
	//求出两个顶点的下标位置
	int p1 = GetVertexPos(g,v1);
	int p2 =  GetVertexPos(g,v2);
	if(p1==-1 || p2==-1)
		return;

	if(g->Edge[p1][p2] == 0)
		return;

	//将边清空
	g->Edge[p1][p2] = g->Edge[p2][1] = 0;
	g->NumEdges--; //更新边数
}

//删除顶点
void RemoveVertex(GraphMtx *g, T v)
{
	//获取顶点的位置
	int p = GetVertexPos(g,v);
	if(p == -1)
		return;

	
	//释放顶点
	int numedges = 0;

	for(int i=p; i<g->NumVertices-1; ++i)
	{
		//将要释放顶点之后的顶点逐一前移
		g->VerticesList[i] = g->VerticesList[i+1];
	}

	//统计与要删除顶点相连的边条数
	for(i=0; i<g->NumVertices; ++i)
	{
		if(g->Edge[p][i] != 0)
		{
			numedges++;
		}
	}

	//删除与释放顶点相连的边（更改存放边信息的矩阵）
	for(i=p; i<g->NumVertices-1; ++i)
	{
		//将要删除行之后的行逐一向前移动一行
		for(int j=0; j<g->NumVertices; ++j)
		{
			g->Edge[i][j] = g->Edge[i+1][j];
		}
	}

	for(i=p; i<g->NumVertices; ++i)//删除列
	{
		//将要删除列之后的列逐一向前移动一列
		for(int j=0; j<g->NumVertices; ++j)
		{
			g->Edge[j][i] = g->Edge[j][i+1];
		}
	}
	g->NumVertices--;
	g->NumEdges -= numedges;
}

//销毁图
void DestroyGraph(GraphMtx *g)
{
	//释放顶点
	free(g->VerticesList);
	g->VerticesList = NULL;
	//释放边存储结构的列
	for(int i=0; i<g->NumVertices; ++i)
	{
		free(g->Edge[i]);
	}
	free(g->Edge);//释放存放行指针的空间
	g->Edge = NULL;
	g->MaxVertices = g->NumEdges = g->NumVertices = 0;
}

//获取v第一个邻接顶点
int  GetFirstNeighbor(GraphMtx *g, T v)
{
	//获取顶点v所在位置
	int p = GetVertexPos(g,v);
	if(p == -1)
		return -1;

	//对顶点进行搜索，看那个顶点与v相连
	for(int i=0; i<g->NumVertices; ++i)
	{
		//判断是否，找到
		if(g->Edge[p][i] == 1)
			return i; //找到即返回
	}
	return -1;
}

//获取下一个邻接顶点：获取顶点v的邻接顶点（该邻接点的顺序在邻接点w之后）
int  GetNextNeighbor(GraphMtx *g, T v, T w)
{
	//获取v和w所在位置
	int pv = GetVertexPos(g,v);
	int pw = GetVertexPos(g,w);
	if(pv==-1 || pw==-1)
		return -1;

	//从v的邻接顶点w的位置向后搜索，找到第一个与v相邻的顶点，即所求
	for(int i=pw+1; i<g->NumVertices; ++i)
	{
		
		if(g->Edge[pv][i] == 1)
			return i; 
	}
	return -1;
}

//获取边的权重
E    GetWeight(GraphMtx *g, int v1, int v2)
{
	if(v1==-1 || v2==-1)
		return MAX_COST;
	return g->Edge[v1][v2];
}

//通过Prim算法获取最小生成树，其中g为邻接矩阵表示的图，vertex为生成树的起点
void MinSpanTree_Prim(GraphMtx *g, T vertex)
{
	int n = g->NumVertices; //获取图的顶点个数
	//lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
	E *lowcost = (E*)malloc(sizeof(E)*n); //lowcost[n] 
	//mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=-1表示起点 i 加入MST
	int *mst = (int *)malloc(sizeof(int)*n);//mst[n]
	assert(lowcost!=NULL && mst!=NULL);

	//初始化lowcost和mst
	int k = GetVertexPos(g,vertex);//获取顶点的位置
	for(int i=0; i<n; ++i)
	{
		if(i != k)
		{
			
			lowcost[i] = GetWeight(g,k,i); //保存边值	
			mst[i] = k; //保存顶点
		}
		else
		{
			lowcost[i] = 0; //保存边值,表示i点加入了MST
			mst[i] = -1; //保存顶点,表示i点加入了MST
		}
	}

	int min,min_index;
	int begin,end;
	E cost;

	for(i=0; i<n-1; ++i)
	{
		min = MAX_COST;
		min_index = -1;
		//寻找最小的花费代价，并且记录对应的终止顶点
		for(int j=0; j<n; ++j)
		{
			
			if(lowcost[j]!=0 && lowcost[j]<min)
			{//顶点未加入到数组中且边的权值小于最小值			
				min = lowcost[j];
				min_index = j;
			}
		}
		//获取查找到的权值最小边的起始位置和终止位置
		begin = mst[min_index]; //起始顶点位置
		end = min_index; //终止顶点位置
		printf("%c-->%c : %d\n",g->VerticesList[begin],g->VerticesList[end],min);//最小生成树的顶点和边
		//将找到权值最小边的终止顶点标记为已经处理
		lowcost[min_index] = 0;
		mst[min_index] = -1;

		//查询与新加入的顶点相连接的边是否有存在更短的，有的话就需要进行记录
		for(j=0; j<n; ++j)
		{
			cost = GetWeight(g,min_index,j);
			if(cost < lowcost[j])
			{
				lowcost[j] = cost;
				mst[j] = min_index;
			}
		}
	}
}

到了这里，关于图之最小生成树Prim算法详解(C语言版)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • C语言实现最小生成树算法：Prim和Kruskal

    以下是使用C语言实现Prim算法生成最小生成树的代码： 注释如下： #include stdio.h 和 `#include #define V 5 定义了图中顶点的个数为5。 int minDistance(int dist[], int visited[]) 函数用于找到顶点集合中未访问的顶点中距离最小的顶点。输入参数 dist 用于存储顶点到最小生成树的距离，输入

    2024年02月03日
    浏览(41)
  • 【数据结构与算法】最小生成树之普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法

    【数据结构与算法】最小生成树之普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法

      🌱博客主页：大寄一场. 🌱系列专栏：数据结构与算法 😘博客制作不易欢迎各位👍点赞+⭐收藏+➕关注 目录 前言 一、最小生成树的概念 二、最小生成树的求解方法 三、练习题 四、最小生成树在实际应用中的例子 最近非科班的同学学到了最小生成树并询问我，于是想趁

    2024年02月07日
    浏览(41)
  • 【数据结构】最小生成树(Prim算法,普里姆算法,普利姆)、最短路径(Dijkstra算法，迪杰斯特拉算法，单源最短路径)

    【数据结构】最小生成树(Prim算法,普里姆算法,普利姆)、最短路径(Dijkstra算法，迪杰斯特拉算法，单源最短路径)

    问题解答 （1）最小生成树（Minimal Spanning Tree）的定义 生成树的代价 ：设 G ( V , E ) G(V,E) G ( V , E ) 是一个无向连通网图，生成树上 各边的权值之和 称为 生成树的代价 。 最小生成树 ：在图 G G G 所有生成树中， 代价最小的生成树 为 最小生成树 。 （2）最小生成树（MST）的性

    2024年02月11日
    浏览(38)
  • 考研算法复试刷题19天：Prim算法求最小生成树 【prim,最小生成树】

    考研算法复试刷题19天：Prim算法求最小生成树 【prim,最小生成树】

    参考博客：图解：什么是最小生成树？ - 知乎 (zhihu.com)  总结下来的过程就是，一张图，我们将他化为树的形式，也就是生成树。那么最小生成树有是啥呢？ 所谓一个 带权图 的最小生成树，就是原图中边的权值最小的生成树 ，所谓最小是指边的权值之和小于或者等于其它

    2024年02月07日
    浏览(63)
  • 最小生成树—Prim算法

    最小生成树—Prim算法

    我们要讨论的问题是如何在一个 无向图 中找到它的最小生成树，虽然这个问题对有向图也有意义，但是处理起来更麻烦。 一个无向图 G 的最小生成树就是连接 G 上所有顶点的边构成的树，且这些边的总权值最低。当且仅当图是 连通的 才有最小生成树。 在无向图的最小生成

    2024年02月09日
    浏览(48)
  • 贪心算法：最小生成树Prim算法

    贪心算法：最小生成树Prim算法

    👨‍🎓作者简介：一位喜欢写作，计科专业大二菜鸟 🏡个人主页：starry陆离 🕒首发日期：2022年5月31日星期二 🌌上期文章：动态规划:多重背包问题 📚订阅专栏：算法分析与设计 如果文章有帮到你的话记得点赞👍+收藏💗支持一下哦 这是大一暑假的c笔记，再一次写pri

    2024年02月01日
    浏览(50)
  • 最小生成树——prim算法实现

    最小生成树——prim算法实现

    N个城市之间需要铺设一张交通网，使任意两个城市间都有交通路线直达，现已知各个城市之间铺设道路的经济成本，问该如何求算铺网的最低经济成本？为求算最低经济成本，可以假设N个城市就是连通网G的N个顶点，而求算最低成本问题可以转化为在N个城市间找到N-1条边，

    2024年02月08日
    浏览(36)
  • Prim算法求最小生成树

    Prim算法求最小生成树

    给定一张边带无权的无向图G = （V， E）， n = |V|， m = |E|。由V中全部n个顶点和E中n - 1条边构成的无向连通子图被称为G的一课生成树。边的权值之和最小的生成树被称为无向图的最小生成树。 Prim算法总是维护最小生成树的一部分。最初，Prim算法仅确定1号节点属于最小生成树

    2024年02月12日
    浏览(42)
  • Prim算法实现最小生成树

    Prim算法实现最小生成树

    例如：要在n个城市之间铺设光缆，主要目标是要使这n个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。 将图中所有顶点分为两类：树顶点（已

    2024年02月11日
    浏览(42)
  • 最小生成树(Prim算法,Kruskal算法）

    最小生成树(Prim算法,Kruskal算法）

    （1）生成树： 如果在一个无向连通图不包含回路（连通图中不存在环），则为一个树 （2）最小生成树（minimal spanning tree）： 在一个图所有生成树中，代价最小的生成树称为最小生成树 （3）生成树的代价： 在一个无向连通网中，生成树各边的权值之和称为该生成树的代价

    2024年02月08日
    浏览(43)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包