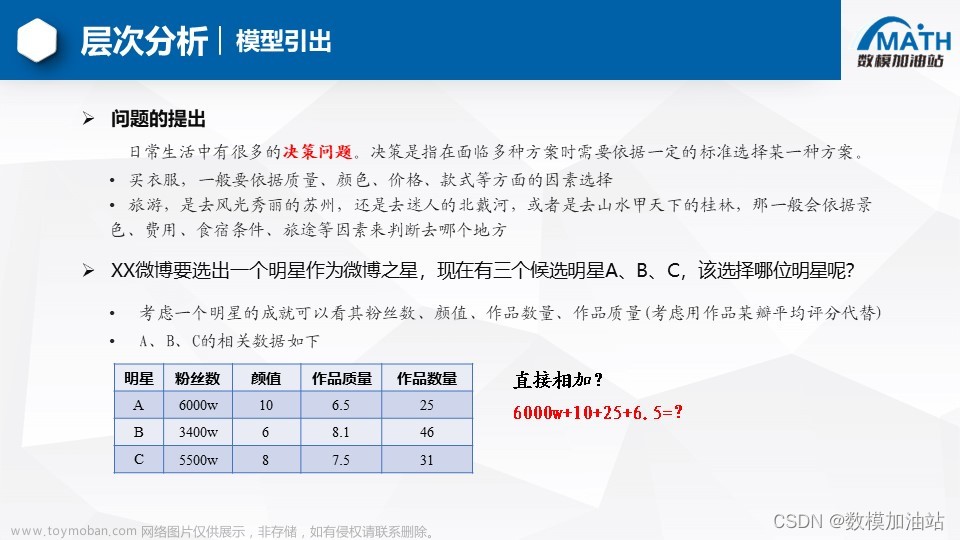
02 论文提供的太阳镜的评价体系
03 建立目标层和准则层的判断矩阵 (论文提供)
04 首先需要对判断矩阵进行一致性检验
4.1 一致性检验的一般步骤
4.2 对应上方步骤的变量和代码
05 一致性检验通过之后开始计算权重
5.1 算术平均法计算权重-理论部分
5.2 算术平均法计算权重-代码部分
5.3 几何平均法计算权重-理论部分
5.4 几何平均法计算权重-代码部分
5.5 特征值法计算权重-理论部分
5.6 特征值法计算权重-代码部分
5.7 总结
06 后续的权重组合思路
本博客以 许学敏的《层次分析法在太阳镜产品质量评价中的应用》为例进行讲解。

02 论文提供的太阳镜的评价体系

03 建立目标层和准则层的判断矩阵 (论文提供)
我们以该判断矩阵为例说明如何进行判断矩阵的一致性检验和权重计算,至于其它的判断矩阵也是如此。

04 首先需要对判断矩阵进行一致性检验
4.1 一致性检验的一般步骤

4.2 对应上方步骤的变量和代码

% 层次分析法求取权重
% 进行目标层和准则层的判断矩阵的一致性检验
% 获取矩阵的行列号
[row, col] = size(m_z_matrix);
% 获取该判断矩阵的特征值和特征向量
[vec, eig_value] = eig(m_z_matrix); % vec表示特征向量, eig_value表示特征值
% 获取最大的特征值
max_eig_value = max(max(eig_value)) % 特征值不是给出一个list,而是一个特征值分布在对角线上的矩阵,所以要获取最大值需要两次max
% 计算CI
CI = (max_eig_value - row) / (row - 1);
% RI list
RI_list = [0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
% 计算RI
RI = RI_list(row);
% 计算CR
CR = CI ./ RI % 若CR小于0.1,那么一致性检验通过
% 最大特征值为6.3674, CR为0.0583<0.1,一致性检验通过,开始计算权重05 一致性检验通过之后开始计算权重
三种权重的计算方法:算术平均法、几何平均法、特征值法
5.1 算术平均法计算权重-理论部分

5.2 算术平均法计算权重-代码部分
% 算术平均法求取权重
weight1 = sum((m_z_matrix ./ repmat(sum(m_z_matrix, 1), row, 1)), 2) / row5.3 几何平均法计算权重-理论部分

5.4 几何平均法计算权重-代码部分
% 几何平均法求取权重
temp = prod(m_z_matrix, 2) .^ (1 / row); % prod(矩阵, dim)若dim=2表示按行计算乘积,1表示按列计算乘积;如果不是矩阵只是向量,那么返回向量所有元素的乘积
% 进行归一化处理
weight2 = temp ./ sum(temp)5.5 特征值法计算权重-理论部分

5.6 特征值法计算权重-代码部分
% 特征值法求取权重(论文使用的是该种方法,论文中A-B判断矩阵中的权重与该代码运行结果完全一致)
% 思路:先获取判断矩阵的特征值和特征向量,在获取最大特征值对应的特征向量,最后对该特征向量进行归一化处理
[vec, eig_value] = eig(m_z_matrix); % V为特征向量,D为特征值
max_eig_value = max(max(eig_value)); % 获取最大的特征值
% 上述两步其实可以不写,因为一致性检验已经写过了
[r, c] = find(eig_value == max_eig_value, 1); % 获取最大特征值所在的行列号, 参数1表示只取第一个
temp_weight = vec(:, c); % 获取最大特征值对应的特征向量
disp('特征值法求得的权重为:')
weight3 = temp_weight ./ sum(temp_weight) % 对特征向量归一化处理即可得到权重5.7 总结
这是目标层与准则层之间的判断矩阵的计算方法,对于最后我们有三种方法求取得到了准则层的权重,所以最后我们可以对三种方法得到的权重取平均值,或者就使用某一种方法得到的权重也是可以的(一般特征值法比较多,不知道是不是因为matlab求取比较简单所以用的多,其实前两种方法的代码会更难理解)。
06 后续的权重组合思路
之后就是准则层与方案层之间的判断矩阵的权重计算,也是如上类似的,甚至于你只需要修改矩阵变量无需修改其它代码部分。
最后就是对于目标层与方案层之间的权重计算(很简单)

这是关于层次分析法如何求取判断矩阵的的权重的完整代码
% 层次分析法求取权重
% 进行目标层和准则层的判断矩阵的一致性检验
% 获取矩阵的行列号
[row, col] = size(m_z_matrix);
% 获取该判断矩阵的特征值和特征向量
[vec, eig_value] = eig(m_z_matrix); % vec表示特征向量, eig_value表示特征值
% 获取最大的特征值
max_eig_value = max(max(eig_value)) % 特征值不是给出一个list,而是一个特征值分布在对角线上的矩阵,所以要获取最大值需要两次max
% 计算CI
CI = (max_eig_value - row) / (row - 1);
% RI list
RI_list = [0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
% 计算RI
RI = RI_list(row);
% 计算CR
CR = CI ./ RI % 若CR小于0.1,那么一致性检验通过
% 最大特征值为6.3674, CR为0.0583<0.1,一致性检验通过,开始计算权重
% 算术平均法求取权重
weight1 = sum((m_z_matrix ./ repmat(sum(m_z_matrix, 1), row, 1)), 2) / row % 卫东需要提供标准公式(论文或许)
% 几何平均法求取权重
temp = prod(m_z_matrix, 2) .^ (1 / row); % prod(矩阵, dim)若dim=2表示按行计算乘积,1表示按列计算乘积;如果不是矩阵只是向量,那么返回向量所有元素的乘积
% 进行归一化处理
weight2 = temp ./ sum(temp)
% 特征值法求取权重(论文使用的是该种方法,论文中A-B判断矩阵中的权重与该代码运行结果完全一致)
% 思路:先获取判断矩阵的特征值和特征向量,在获取最大特征值对应的特征向量,最后对该特征向量进行归一化处理
[vec, eig_value] = eig(m_z_matrix); % V为特征向量,D为特征值
max_eig_value = max(max(eig_value)); % 获取最大的特征值
% 上述两步其实可以不写,因为一致性检验已经写过了
[r, c] = find(eig_value == max_eig_value, 1); % 获取最大特征值所在的行列号, 参数1表示只取第一个
temp_weight = vec(:, c); % 获取最大特征值对应的特征向量
disp('特征值法求得的权重为:')
weight3 = temp_weight ./ sum(temp_weight) % 对特征向量归一化处理即可得到权重
如果有问题,欢迎一起探讨。文章来源:https://www.toymoban.com/news/detail-779232.html
<p>炒茄子</p>文章来源地址https://www.toymoban.com/news/detail-779232.html
到了这里,关于Matlab:如何利用层次分析法(升级版)计算具有多重指标的判断矩阵的一致性检验和权重的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!