「数据结构」八大排序1-Toy模板网

这篇具有很好参考价值的文章主要介绍了「数据结构」八大排序1。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🎇个人主页：Ice_Sugar_7
🎇所属专栏：初阶数据结构
🎇欢迎点赞收藏加关注哦！

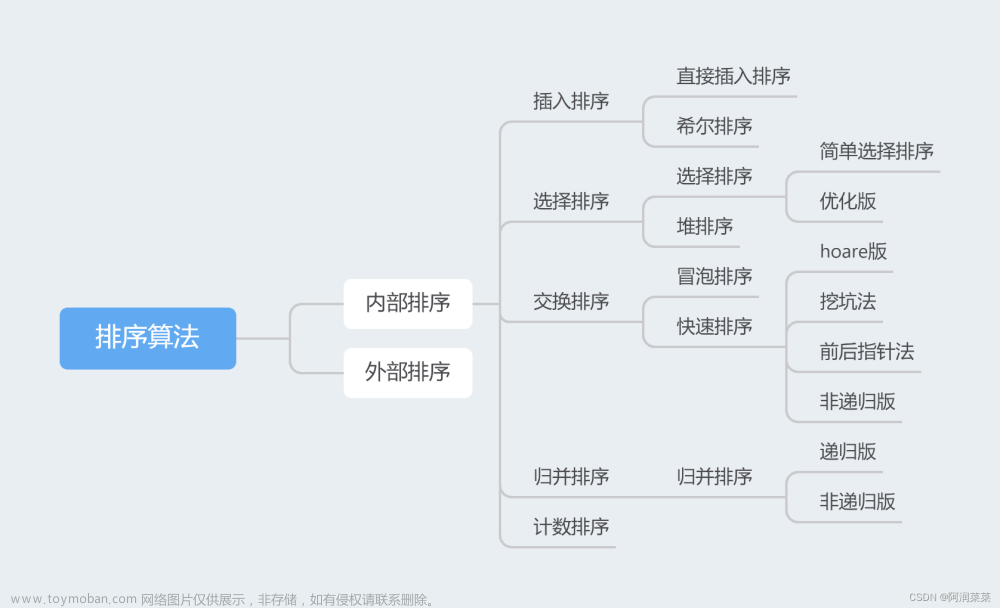
🍉插入排序

插排就是将一个元素插入一个有序序列中合适的位置，分为直接插入排序和希尔排序

🍌直接插入排序

流程如下：
①保存待插入的值：假设某一趟中有序序列最后一个元素下标为end，先保存（end+1）位置的元素，保存到临时变量tmp。

②为a[end+1]找到合适的位置：使用while循环，里面比较a[end]和a[end+1]的大小。
若前者<后者，就退出循环
反之，则将a[end]往后挪一位，覆盖掉a[end+1]，end减1，然后让tmp继续往前找，直到找到比它小的元素或者end < 0（end<0说明所有元素都比tmp大，那么就应该把tmp放在a[0]），插到该元素后面。
简而言之就是让tmp向前找比它小的元素，找到就插在它的后面；找不到就是插在第一位

③至此，我们排好了一个数据，现在要排列所有元素，只需在外面套上一层for循环
（假设数组有n个元素，注意循环的终止条件是i < n-1，即i最多只能取到n-2，因为是 i 和 i+1 进行比较）

比如：

int a[] = {2,7,1,9,6,5,8};

图解如下：
「数据结构」八大排序1,初阶数据结构,数据结构,排序算法,算法

代码如下：

//n为数组元素个数
void InsertSort(int* a, int n) {
	for (int i = 0; i < n-1; i++) {
		int end = i;  //end为有序序列最后一个元素的下标
		int tmp = a[end + 1];  //tmp保存待插入的数据
		while (end >= 0)
		{
			if (a[end + 1] < a[end]) //待插入的数比end小，那么end就向后移动，给待插入的数据挪出位置
				a[end + 1] = a[end];
			else
				break;
			end--;  //更新end，向前找小 
		}
		//找到小或end == -1
		a[end + 1] = tmp;
	}
}

🥝复杂度及稳定性

时间复杂度：第一趟1次，第二趟2次……由等差数列公式可以推出是O（N^2）
空间复杂度：O（1）
稳定性：稳定

🍌希尔排序

希尔排序是直接插入排序的优化。分两步完成：预排序+直接插入排序
预排序的意义：让大的数更快到后面，小的数更快到前面。使序列趋于有序，降低直接插入排序的成本

🥝预排序

直接插入排序是让相邻的元素进行比较。预排序则是让一个元素和与它相隔几个位置的元素比较
比如：

int a[] = {9,1,2,5,7,4,8,6,3,5};

「数据结构」八大排序1,初阶数据结构,数据结构,排序算法,算法
9、5、8、5可以分为一组；1、7、6也是一组；2、4、3同理
同一组的元素进行比较，排好序。
预排序后得到：

这样就完成了一次预排序。希尔排序中有多次预排序，每次排完后会缩小间隔、重新分组，然后继续预排序。假设最开始的间隔为gap，那么就一直缩小，gap越小，预排序一次后序列就越趋于有序。直到gap为1，此时就是直接插入排序，这一次排好后序列就有序了

gap每次预排序一般是缩小到上一次的一半，或是1/3（注意gap除以3之后需要+1，保证gap不为0）
代码如下：

void ShellSort(int* a, int n) {
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;  //+1确保gap至少为1，最后一次循环gap == 1
		//一次预排序
		for (int i = 0; i < n - gap; i++)  //i+gap最多取到n-1
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
					a[end+gap] = a[end];
				else
					break;
				end -= gap;
			}
			a[end + gap] = tmp;
		}
	}
}

🥝复杂度及稳定性

时间复杂度：O(N^1.3)
空间复杂度：O（1）
稳定性：不稳定。因为预排序很容易就把相同的数的相对顺序打乱了

🍉选择排序

排序思路：
●假设序列最左边、右边下标分别为begin、end
●从序列中找出最大、最小值，并分别将它们放到下标为begin、end的地方
●找出第二大和第二小，分别放到begin+1、end-1
●剩下元素也按照这样排列

在“交换位置”这一步有一个很坑的点，如果最小值刚好在end，那就会和最大值交换位置，但是此时我们的mini仍然在end，直接交换a[mini]和a[begin]就会把最大值和begin处的元素交换位置
所以在最大值和a[end]交换之后检查一下，看mini是否在end处。如果是，就将maxi赋值给mini（因为此时maxi指向的就是最小值）

void SelectSort(int* a, int n) {
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int mini = begin,maxi = begin;
		for (int i = begin + 1; i <= end; i++)
		{
			if (a[maxi] < a[i])
				maxi = i;
			if (a[mini] > a[i])
				mini = i;
		}
		Swap(&a[maxi], &a[end]);
		if (end == mini)  //让mini重新指向最小值
			mini = maxi;
		Swap(&a[mini], &a[begin]);
		++begin;
		--end;
	}
}

🍌复杂度及稳定性

时间复杂度：第一趟走（n-2）次，第二趟走（n-4）次，第 i 趟走（n-2*i）次……由等差数列公式，可以得出时间复杂度为O（N^2）
空间复杂度：O（1）
稳定性：不稳定。比如1 9 9 4 2 1 3 6，第一趟第一个9就会被换到最后面

🍉堆排序

前面的文章有讲过，升序建大堆，降序建小堆
比如排升序，就建大堆，然后让堆顶元素和堆中最后一个元素交换位置，再进行调整

void HeapSort(int* a, int k) {  //a为给定数组
	for (int i = (k - 1 - 1) / 2; i >= 0; i--) {   //调整为一个堆
		AdjustDown(a, k, i);
	}

	for (int i = k - 1; i >= 0; i--) {  //采用删除结点的思想，先交换，再调整
		Swap(a[0], a[i]);
		AdjustDown(a, i, 0);
	}
}