解决背包衍生题目：单词拆分和分割等和子集--动态规划方式深度呈现

目录

139. 单词拆分

解题思路

代码实现

416. 分割等和子集

二维动态规划

状态压缩(一维)

问题拓展

背包九讲知识总结

相关问题

139. 单词拆分

题目描述

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。

注意，你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

提示：

• 1 <= s.length <= 300
• 1 <= wordDict.length <= 1000
• 1 <= wordDict[i].length <= 20
• s 和 wordDict[i] 仅由小写英文字母组成
• wordDict 中的所有字符串 互不相同

解题思路

dp[i] 表示字符串 s 的前 i 个字符是否可以用 wordDict 中的单词拼接得到。

解题步骤如下：

1. 初始化一个大小为 s.length() + 1 的布尔数组 dp，并将 dp[0] 设置为 true，表示空字符串总是可以拼接的。

2. 对于每个从 1 到 s.length() 的索引 i，遍历检查：

   • 对于每个在 wordDict 中的单词 word，如果 word 的长度小于等于 i 且 dp[i - word.length()] 为 true，则检查 s 从位置 i - word.length() 到 i 的子串是否等于 word。
   • 如果这个子串等于 word，则将 dp[i] 设置为 true。

3. 在完成上述步骤后，dp[s.length()] 将给出答案，表示整个字符串 s 是否可以由 wordDict 中的单词拼接得到。

代码实现

import java.util.List;


public class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        boolean[] dp = new boolean[s.length() + 1];
        dp[0] = true;

        for (int i = 1; i <= s.length(); i++) {
            for (String word : wordDict) {
                if (word.length() <= i) {
                    if (dp[i - word.length()]) {
                        if (s.substring(i - word.length(), i).equals(word)) {
                            dp[i] = true;
                            break;
                        }
                    }
                }
            }
        }
        return dp[s.length()];
    }
}

416. 分割等和子集

题目描述

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

二维动态规划

状态转移方程：很多时候，状态转移方程思考的角度是「分类讨论」，对于「0-1 背包问题」而言就是「当前考虑到的数字选与不选」。

dp[i][j]表示从数组的 [0, i] 这个子区间内挑选一些正整数，每个数只能用一次，使得这些数的和恰好等于 j。

1. 不选择 nums[i]，如果在 [0, i - 1] 这个子区间内已经有一部分元素，使得它们的和为 j ，那么 dp[i][j] = true；
2. 选择 nums[i]，如果在 [0, i - 1] 这个子区间内就得找到一部分元素，使得它们的和为 j - nums[i]。

状态转移方程：

dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i]]

以下是解决这个问题的步骤： 

1. 计算总和：首先，计算数组 nums 的总和。如果总和是奇数，那么不能分割成两个和相等的子集，因为两个整数和不能为奇数。

2. 初始化动态规划数组：创建一个布尔型动态规划数组 dp，其大小为 sum / 2 + 1。dp[i][j]表示从数组的 [0, i] 这个子区间内挑选一些正整数，每个数只能用一次，使得这些数的和恰好等于 j。初始化 dp[0] 为 true，因为总和为 0 总是可能的。

3. 填充动态规划数组：对于 nums 中的每个数字 num，从 sum / 2 到 num 倒序遍历 dp 数组，更新 dp[j] = dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]

4. 检查结果：最后，返回 dp[len - 1][target]的值。如果 dp[len - 1][target] 为 true，表示可以分割数组成两个和相等的子集。 

public class Solution {
    public boolean canPartition(int[] nums) {
        int len = nums.length;
        // 计算数组总和
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        // 如果总和是奇数，无法平分为两个和相等的子集
        if ((sum & 1) == 1) {
            return false;
        }

        int target = sum / 2;
        // 创建动态规划数组，dp[i][j] 表示使用前 i 个数字能否得到总和 j
        boolean[][] dp = new boolean[len][target + 1];

        //初始化第一行，只使用第一个数字 nums[0] 时，能达到的总和
        //防止数组越界要加个判断
        if (nums[0] <= target) {
            dp[0][nums[0]] = true;
        }

        // 动态规划，填充剩余的表格
        for (int i = 1; i < len; i++) {
            for (int j = 0; j <= target; j++) {
                // 先从上一行继承结果
                dp[i][j] = dp[i - 1][j];

                // 如果当前数字等于目标值 j，直接标记为 true
                if (nums[i] == j) {
                    dp[i][j] = true;
                    continue;
                }
                // 如果当前数字小于 j，考虑两种情况：不取或取当前数字
                if (nums[i] < j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }
        }
        // 返回最终结果，即使用所有数字是否能达到总和 target
        return dp[len - 1][target];
    }
}

状态压缩(一维)

本质上，这个问题是一个子集求和问题，类似于背包问题。问题可以被转化为：是否可以从数组中选择一些数字，使得这些数字的总和等于数组所有元素总和的一半。

dp[i] 表示数组是否可以形成总和为 i 的子集。初始化 dp[0] 为 true，因为总和为 0 总是可能的。

public class Solution {
    public boolean canPartition(int[] nums) {
        // 计算数组总和
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        // 如果总和是奇数，则不能分割成两个和相等的子集
        if (sum % 2 != 0) {
            return false;
        }

        // 计算子集总和目标值（数组总和的一半）
        sum /= 2;

        // 初始化动态规划数组
        boolean[] dp = new boolean[sum + 1];
        dp[0] = true; // 总和为0总是可能的

        // 遍历数组中的每个数字
        for (int i = 1; i < len; i++) {
            // 从子集总和目标值向下遍历到当前数字
            for (int j = sum; nums[i] <= j; j--) {
                // 更新动态规划数组的值
                // dp[j] = true 代表不包含当前考虑的 num 就已经能组成子集

                //dp[j - num] = true  代表的是包含当前考虑的 num 的解
                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }

        // 如果dp[sum]为true，则表示可以分割数组成两个和相等的子集
        return dp[sum];
    }
}

思考：为什么压缩到一维时，内循环要采用逆序？

因为在一维情况下，是根据 dp[j] || dp[j - nums[i]]来推d[j]的值，如不逆序，就无法保证在外循环 i 值保持不变 j 值递增的情况下，dp[j - num[i]]的值不会被当前所放入的nums[i]所修改，当j值未到达临界条件前，会一直被nums[i]影响，也即是可能重复的放入了多次nums[i]，为了避免前面对后面产生影响，故用逆序。

举个例子，数组为[2,2,3,5]，要找和为6的组合

• i = 0时，dp[2]为true，
• 当i自增到1，j = 4时，nums[i] = 2,dp[4] = (dp[4] || dp[4 - 2]) 为true，
  • 当i不变，j = 6时,dp[6] = dp [6] || dp [6 - 2],而dp[4]为true，

所以dp[6] = true,显然是错误的。 如果是正序的话，后面dp访问前面的dp时得到的是已经更新的内故必须得纠正在正序时，i值不变时多次放入nums[i]影响后续判断的情况。

但如果我们逆序遍历 j：

• 当 i = 1，nums[i] = 2，逆序遍历 j：
  • 当 j = 6，dp[6] = dp[6] || dp[6 - 2]，此时 dp[6 - 2] 即 dp[4] 还没有被当前的 nums[i] 更新，所以这是基于 i = 0 时的结果。
  • 接下来，当 j = 4，更新 dp[4]，但这个更新不会影响到 j = 6 的计算。

逆序遍历保证了在计算 dp[j] 时，我们使用的 dp[j - nums[i]] 是基于之前元素的结果，而不是当前元素 nums[i] 的结果。这样就避免了重复计算同一个元素。

问题拓展

这道题本质是个子集求和问题:求nums的一个子集他们的和是target。

第 494 题：目标和也可以转为为子集求和数学推导略，下面是子集求和的代码模板。

// 创建动态规划数组，dp[i] 表示和为 i 的子集的数量
int[] dp = new int[target + 1];
// 初始化，和为0的方式有一种（不选择任何元素）
dp[0] = 1;

// 遍历nums中的每个数字
for (int num : nums) {
    // 从新目标开始向下更新dp数组
    for (int i = target; i >= num; i--) {
         // 更新dp[i]：加上当前数字num能够达到的子集数
         dp[i] += dp[i - num];
    }
}

// 返回达到新目标的子集数
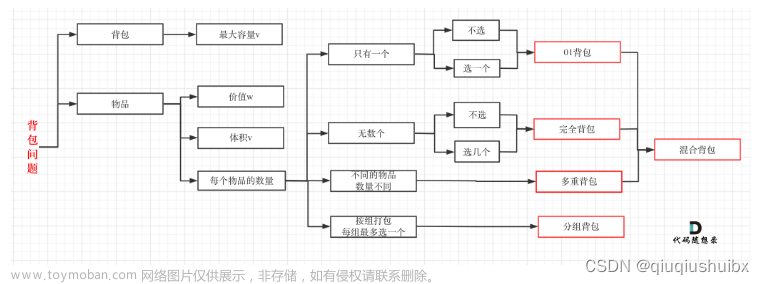
return dp[target];

背包九讲知识总结

1. 0-1背包问题：这是最基本的形式，每件物品都是独一无二的，可以选择放入或不放入。状态F[i, v]表示将前i件物品放入容量为v的背包可以获得的最大价值。状态转移方程为F[i, v] = max{F[i − 1, v], F[i − 1, v − Ci] + Wi}(内循环用逆序)。

2. 完全背包问题：与01背包问题类似，但每种物品可以被多次选择。状态转移方程需要改变，以适应同一物品可以多次选择的可能性(内循环用顺序)。

3. 多重背包问题：涉及可以多次选择但有特定限制的物品。解决方案可以通过将其转换为01背包问题或使用单调队列实现O(VN)的解决方案。

4. 混合三种背包问题：涉及01背包、完全背包和多重背包问题的混合。解决策略根据物品类型的不同而变化，对不同类型的物品使用不同的循环。

5. 二维费用的背包问题：为每件物品引入第二种成本维度。解决方案涉及为状态添加额外的维度以适应附加成本。

6. 分组的背包问题：物品被划分为组，每组内的物品相互冲突，每组最多选择一件。解决方案涉及将每组视为单独实体，并对每组应用背包解决方案。

7. 有依赖的背包问题：涉及选择某些物品依赖于选择其他物品。解决方案是通过将依赖物品转换为组，并将其解决为分组背包问题。

8. 泛化物品：这个概念处理的是成本和价值不固定但随分配的成本变化的物品。这是对背包问题的更抽象的处理方式。

9. 背包问题问法的变化：这一部分讨论了提出背包问题的不同方式，例如找出填满背包的方法数、最小化总价值或找出字典序最小的最优解。

链接: 网盘地址 提取码: tcnq 

相关问题

「力扣」上的 0-1 背包问题：

「力扣」第 416 题：分割等和子集（中等）；
「力扣」第 474 题：一和零（中等）；
「力扣」第 494 题：目标和（中等）；
「力扣」第 879 题：盈利计划（困难）；

「力扣」上的 完全背包问题：

「力扣」第 322 题：零钱兑换（中等）；
「力扣」第 518 题：零钱兑换 II（中等）；
「力扣」第 1449 题：数位成本和为目标值的最大数字（困难）。
 文章来源地址https://www.toymoban.com/news/detail-780093.html

到了这里，关于解决背包衍生题目：单词拆分和分割等和子集--动态规划方式深度呈现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！