数据结构学习笔记(王道)
PS:本文章部分内容参考自王道考研数据结构笔记
一、绪论
1.1. 数据结构
-
数据:是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
-
数据元素:数据的基本单位,一个数据元素可由若干数据项组成。
-
数据项:数据的不可分割的最小单位。
-
数据对象:性质相同的数据元素的集合,是数据的一个子集。
-
数据结构:指互相之间存在着一种或多种特定关系的数据元素的集合,包括逻辑结构,存储结构和对数据的运算。(数据元素都不是孤立存在的)。
-
抽象数据类型(ADT):指一个数学模型以及定义在该模型上的一组操作,只取决于它的一组逻辑特性,用一个三元组表示(D, S, P)。
-
数据类型:是程序设计语言中的一个概念,它是一个值的集合和操作的集合。
-
逻辑结构:是指数据之间关系的描述,与数据的存储结构无关。分为线性结构和非线性结构,通常分为四类结构:
- 集合:结构中的数据元素除了同属于一种类型外,别无其它关系。
- 线性结构:结构中的数据元素之间存在一对一的关系。
- 树型结构:结构中的数据元素之间存在一对多的关系。
- 图状结构(网状结构):结构中的数据元素之间存在多对多的关系。
-
存储结构:是指数据结构在计算机中的表示,又称为数据的物理结构。它包括数据元素的表示和关系的表示,通常由四种基本的存储方法实现:
- 顺序存储方式。数据元素顺序存放,每个存储结点只含一个元素,存储位置反映数据元素间的逻辑关系,存储密度大。有些操作(如插入、删除)效率较差。
- 链式存储方式。每个存储结点除包含数据元素信息外还包含一组(至少一个)指针,指针反映数据元素间的逻辑关系。这种方式不要求存储空间连续,便于动态操作(如插入、删除等),但存储空间开销大(用于指针),且不能折半查找。
- 索引存储方式。除数据元素存储在一组地址连续的内存空间外,还需建立一个索引表,索引表中索引指示存储结点的存储位置(下标)或存储区间端点(下标)。
- 散列存储方式。通过散列函数和解决冲突的方法,将关键字散列在连续的有限的地址空间内,并将散列函数的值解释成关键字所在元素的存储地址。其特点是存取速度快,只能按关键字随机存取,不能顺序存取,也不能折半存取。
1.2. 算法
1.2.1. 算法的基本概念
- 算法:是对特定问题求解步骤的一种描述,是指令的有限序列。其中每一条指令表示一个或多个操作。
- 算法的特性:有穷性、确定性、可行性、输入、输出。
- 算法的设计目标:正确性,可读性,健壮性,高效率与低存储量需求。
算法和程序十分相似,但又有区别。程序不一定具有有穷性,程序中的指令必须是机器可执行的,而算法中的指令则无此限制。算法代表了对问题的解,而程序则是算法在计算机上的特定的实现。一个算法若用程序设计语言来描述,则它就是一个程序。
1.2.2. 算法的时间复杂度
-
如何计算:
- 找到一个基本操作(最深层循环)
- 分析该基本操作的执行次数x与问题规模n的关系 x = f ( n ) x=f(n) x=f(n)
- x的数量级 O ( x ) O(x) O(x)就是算法时间复杂度 T ( n ) T(n) T(n): O ( x ) = T ( n ) O(x)=T(n) O(x)=T(n)
-
常用技巧:
-
加法规则: O ( f ( n ) ) + O ( g ( n ) ) = O ( m a x ( f ( n ) , g ( n ) ) ) O(f(n))+O(g(n))=O(max(f(n), g(n))) O(f(n))+O(g(n))=O(max(f(n),g(n)))
-
乘法规则: O ( f ( n ) ) × O ( g ( n ) ) = O ( f ( n ) × g ( n ) ) O(f(n))×O(g(n))=O(f(n)×g(n)) O(f(n))×O(g(n))=O(f(n)×g(n))
-
“常对幂指阶”
O ( 1 ) < O ( l o g 2 n ) < O ( n ) < O ( n l o g 2 n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 n ) < O ( n ! ) < O ( n n ) O(1)<O(log_2n)<O(n)<O(nlog_2n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n) O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
-
-
三种复杂度:
- 最坏时间复杂度:考虑输入数据“最坏”的情况。
- 平均时间复杂度:考虑所有输入数据都等概率出现的情况。
- 最好时间复杂度:考虑输入数据“最好”的情况。
算法的性能问题只有在 n 很大时才会暴露出来
1.2.3. 算法的空间复杂度
-
普通程序:
- 找到所占空间大小与问题规模相关的变量
- 分析所占空间 x 与问题规模 n 的关系 x = f ( n ) x=f(n) x=f(n)
- x 的数量级 O ( x ) O(x) O(x) 就是算法空间复杂度 S ( n ) S(n) S(n)
-
递归程序:
- 找到递归调用的深度x与问题规模n的关系 x = f ( n ) x=f(n) x=f(n)
- x的数量级 O ( x ) O(x) O(x) 就是算法空间复杂度 S ( n ) S(n) S(n)
二、线性表
2.1. 线性表的定义和操作
2.1.1. 线性表的基本概念
-
线性表:是具有相同数据类型的 n 个数据元素的有限序列。
-
特点:
-
存在惟一的第一个元素。
-
存在惟一的最后一个元素。
-
除第一个元素之外,每个元素均只有一个直接前驱。
-
除最后一个元素之外,每个元素均只有一个直接后继。
-
-
线性表的存储结构:
- 顺序存储结构:顺序表
- 链式存储结构:链表
2.1.2. 线性表的基本操作
-
InitList(&L):初始化表。构造一个空的线性表 L,并分配内存空间。 -
DestroyList(&L):销毁表。并释放线性表 L 占用的内存空间。 -
ListInsert(&L, i, &e):插入操作。在表 L 的第 i 个位置插入指定元素 e 。 -
ListDelete(&L, i, &e):删除操作。删除表 L 中第 i 个位置的元素,并用 e 返回删除元素的值。 -
LocateElem(L, e):按值查找。在表 L 中查找具有给定元素值的元素。 -
GetElem(L, i):按位查找。获取表 L 中第 i 个位置的元素的值。 -
Length(L):求表长。返回线性表 L 的长度,即表中元素的个数。 -
PrintList(L):打印表。按顺序输出线性表 L 的所有元素值。 -
Empty(L):判断是否为空。若 线性表L 为空表,则返回 true,否则返回 false。
操作数据结构的思路:创销、增删改查
2.2. 顺序表
2.2.1. 顺序表的基本概念
-
顺序表:用顺序存储的方式实现线性表。顺序存储,将逻辑上相邻的元素存储在相邻的物理位置上。
-
特点:
- 随机访问,即可以在 O ( 1 ) O(1) O(1) 时间内找到第 i 个元素。
- 存储密度高,每个节点只存储数据元素。
- 拓展容量不方便(即使使用动态分配的方式实现,拓展长度的时间复杂度也比较高,因为需要把数据复制到新的区域)。
- 插入删除操作不方便,需移动大量元素: O ( n ) O(n) O(n)
2.2.2. 顺序表的实现
静态实现:
#define MaxSize 10 // 定义最大长度
typedef struct {
int data[MaxSize]; // 使用静态的数组存放数据元素
int length; // 顺序表的当前长度
}SqList;
// 初始化顺序表
void InitList(SqList &L) {
L.length = 0; // 顺序表初始长度为0
}
int main() {
SqList L; // 声明一个顺序表
InitList(L); // 初始化顺序表
return 0;
}
动态实现:
#define InitSize 10 // 顺序表的初始长度
typedef struct {
int *data; // 声明动态分配数组的指针
int MaxSize; // 顺序表的最大容量
int length; // 顺序表的当前长度
}SeqList;
// 初始化顺序表
void InitList(SqList &L) {
// 用malloc函数申请一片连续的存储空间
L.data = (int *)malloc(InitSize * sizeof(int));
L.length = 0;
L.MaxSize = InitSize;
}
// 增加动态数组的长度
void IncreaseSize(SqList &L, int len) {
int *p = L.data;
L.data = (int *)malloc((L.MaxSize+len) * sizeof(int));
for (int i = 0; i < L.length; i++)
L.data[i] = p[i]; // 将数据复制到新区域
L.MaxSize = L.MaxSize + len; // 顺序表最大长度增加len
free(p); // 释放原来的内存空间
}
int main() {
SeqList L; // 声明一个顺序表
InitList(L); // 初始化顺序表
...
IncreaseSize(L, 5);
return 0;
}
malloc()函数的作用:会申请一片存储空间,并返回存储空间第一个位置的地址,也就是该位置的指针。
2.2.3. 顺序表的基本操作
插入:
#define MaxSize 10 // 定义最大长度
typedef struct {
int data[MaxSize]; // 用静态的数组存放数据元素
int length; // 顺序表的当前长度
}SqList;
// 在顺序表i位置插入e
bool ListInsert(SqList &L, int i, int e) {
if (i < 1 || i > L.length+1) // 判断i的范围是否有效
return false;
if (L.length >= MaxSize) // 判断存储空间是否已满
return false;
for (int j = L.length; j >= i; j--) // 将第i个元素之后的元素后移
L.data[j] = L.data[j-1];
L.data[i-1] = e; // 在位置i处放入e
L.length++; // 长度+1
return true;
}
int main() {
SqList L;
InitList(L);
ListInsert(L, 3, 3);
return 0;
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
删除:
#define MaxSize 10
typedef struct {
int data[MaxSize];
int length;
} SqList;
// 删除顺序表i位置的数据并存入e
bool ListDelete(SqList &L, int i, int &e) {
if (i < 1 || i > L.length) // 判断i的范围是否有效
return false;
e = L.data[i-1]; // 将被删除的元素赋值给e
for (int j = i; j < L.length; j++) //将第i个位置后的元素前移
L.data[j-1] = L.data[j];
L.length--;
return true;
}
int main() {
SqList L;
InitList(L);
int e = -1;
if (ListDelete(L, 3, e))
printf("已删除第3个元素,删除元素值为%d\n", e);
else
printf("位序i不合法,删除失败\n");
return 0;
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
按位查找:
// 静态分配的按位查找
#define MaxSize 10
typedef struct {
ElemType data[MaxSize];
int length;
}SqList;
ElemType GetElem(SqList L, int i) {
return L.data[i-1];
}
// 动态分配的按位查找
#define InitSize 10
typedef struct {
ElemType *data;
int MaxSize;
int length;
}SeqList;
ElemType GetElem(SeqList L, int i) {
return L.data[i-1];
}
时间复杂度: O ( 1 ) O(1) O(1)
按值查找:
#define InitSize 10
typedef struct {
ElemType *data;
int MaxSize;
int length;
}SqList;
// 查找第一个元素值为e的元素,并返回其位序
int LocateElem(SqList L, ElemType e) {
for (int i = 0; i < L.length; i++)
if (L.data[i] == e)
return i+1; // 数组下标为i的元素值等于e,返回其位序i+1
return 0; // 没有查找到
}
在《数据结构》考研初试中,手写代码可以直接用“==”,无论 ElemType 是基本数据类型还是结构类型
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
2.3. 链表
2.3.1. 单链表的基本概念

- 单链表:用链式存储实现了线性结构。一个结点存储一个数据元素,各结点间的前后关系用一个指针表示。
- 特点:
- 优点:不要求大片连续空间,改变容量方便。
- 缺点:不可随机存取,要耗费一定空间存放指针。
- 两种实现方式:
- 带头结点,写代码更方便。头结点不存储数据,头结点指向的下一个结点才存放实际数据。
- 不带头结点,麻烦。对第一个数据结点与后续数据结点的处理需要用不同的代码逻辑,对空表和非空表的处理需要用不同的代码逻辑。
2.3.2. 单链表的实现
不带头结点的单链表:
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
//初始化一个空的单链表
bool InitList(LinkList &L){
L = NULL; //空表,暂时还没有任何结点
return true;
}
void test(){
LinkList L; //声明一个指向单链表的头指针
//初始化一个空表
InitList(L);
...
}
//判断单链表是否为空
bool Empty(LinkList L){
return (L==NULL)
}
带头结点的单链表:
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
// 初始化一个单链表(带头结点)
bool InitList(LinkList &L){
L = (LNode *)malloc(sizeof(LNode)); //分配一个头结点
if (L == NULL) //内存不足,分配失败
return false;
L->next = NULL; //头结点之后暂时还没有结点
return true;
}
void test(){
LinkList L; //声明一个指向单链表的头指针
//初始化一个空表
InitList(L);
...
}
//判断单链表是否为空
bool Empty(LinkList L){
if (L->next == NULL)
return true;
else
return false;
}
2.3.3. 单链表的插入
按位序插入(带头结点):
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
//在第i个位置插入元素e
bool ListInsert(LinkList &L, int i, ElemType e){
if(i<1)
return False;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L; //循环找到第i-1个结点
while(p!=NULL && j<i-1){ //如果i>lengh,p最后会等于NULL
p = p->next;
j++;
}
//p值为NULL说明i值不合法
if (p==NULL)
return false;
//在第i-1个结点后插入新结点
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e;
s->next = p->next;
p->next = s;
//将结点s连到p后
return true;
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
按位序插入(不带头结点):
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
//在第i个位置插入元素e
bool ListInsert(LinkList &L, int i, ElemType e){
//判断i的合法性
if(i<1)
return false;
//需要判断插入的位置是否是第1个
if(i==1){
LNode *s = (LNode *)malloc(size of(LNode));
s->data =e;
s->next =L;
L=s; //头指针指向新结点
return true;
}
//i>1的情况与带头结点一样,唯一区别是j的初始值为1
LNode *p; //指针p指向当前扫描到的结点
int j=1; //当前p指向的是第几个结点
p = L;
//循环找到第i-1个结点
while(p!=NULL && j<i-1){ //如果i>lengh,p最后会等于NULL
p = p->next;
j++;
}
//p值为NULL说明i值不合法
if (p==NULL)
return false;
//在第i-1个结点后插入新结点
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
除非特别声明,否则之后的代码都默认为带头结点!
指定结点的后插操作:
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
// 在结点p后插入元素e
bool InsertNextNode(LNode *p, ElemType e){
if(p==NULL){
return false;
}
LNode *s = (LNode *)malloc(sizeof(LNode));
if(s==NULL)
return false;
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
// 按位序插入的函数中可以直接调用后插操作
bool ListInsert(LinkList &L, int i, ElemType e){
if(i<1)
return False;
LNode *p;
//指针p指向当前扫描到的结点
int j=0;
//当前p指向的是第几个结点
p = L;
//循环找到第i-1个结点
while(p!=NULL && j<i-1){
//如果i>lengh, p最后会等于NULL
p = p->next;
j++;
}
return InsertNextNode(p, e)
}
时间复杂度: O ( 1 ) O(1) O(1)
指定结点的前插操作:
如果传入头指针,就可以循环整个链表找到指定结点p的前驱结点q,再对q进行后插操作;
如果不传入头指针,可以在指定结点p后插入一个结点s,并交换两个结点所保存的数据,从而变相实现指定结点的前插操作。
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
// 在结点p前插入元素e
bool InsertPriorNode(LNode *p, ElemType e){
if(p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
// 内存不足分配失败
if(s==NULL)
return false;
// 将s插入结点p之后
s->next = p->next;
p->next = s;
// 交换两个结点中的数据
s->data = p->data;
p->data = e;
return true;
}
时间复杂度: O ( 1 ) O(1) O(1)
2.3.4. 单链表的删除
按位序删除:
typedef struct LNode{
ElemType data;
struct LNode *next;}LNode, *LinkList;
// 删除第i个结点并将其所保存的数据存入e
bool ListDelete(LinkList &L, int i, ElemType &e){
if(i<1)
return false;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L;
//循环找到第i-1个结点
while(p!=NULL && j<i-1){
//如果i>lengh,p和p的后继结点会等于NULL
p = p->next;
j++;
}
if(p==NULL)
return false;
if(p->next == NULL)
return false;
//令q暂时保存被删除的结点
LNode *q = p->next;
e = q->data;
p->next = q->next;
free(q)
return true;
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
删除指定结点:
如果传入头指针,就可以循环整个链表找到指定结点p的前驱结点q,再对p进行删除操作;
如果不传入头指针,可以把指定结点p的后继结点q删除,并使结点p保存结点q存储的数据,从而变相实现删除指定结点的操作。但是如果指定结点p没有后继结点,这么做会报错。
// 删除指定结点p
bool DeleteNode(LNode *p){
if(p==NULL)
return false;
LNode *q = p->next; // 令q指向p的后继结点
// 如果p是最后一个结点,则q指向NULL,继续执行就会报错
p->data = q->data;
p->next = q->next;
free(q);
return true;
}
时间复杂度: O ( 1 ) O(1) O(1)
2.3.5. 单链表的查找
按位查找:
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
// 查找指定位序i的结点并返回
LNode * GetElem(LinkList L, int i){
if(i<0)
return NULL;
LNode *p;
int j=0;
p = L;
while(p!=NULL && j<i){
p = p->next;
j++;
}
return p;
}
// 封装后的插入操作,在第i个位置插入元素e,可以调用查询操作和后插操作
bool ListInsert(LinkList &L, int i, ElemType e){
if(i<1)
return False;
// 找到第i-1个元素
LNode *p = GetElem(L, i-1);
// 在p结点后插入元素e
return InsertNextNode(p, e)
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
按值查找:
// 查找数据域为e的结点指针,否则返回NULL
LNode * LocateElem(LinkList L, ElemType e){
LNode *P = L->next;
// 从第一个结点开始查找数据域为e的结点
while(p!=NULL && p->data != e){
p = p->next;
}
return p;
}
时间复杂度:
- 最好时间复杂度: O ( 1 ) O(1) O(1)
- 最坏时间复杂度: O ( n ) O(n) O(n)
- 平均时间复杂度: O ( n ) O(n) O(n)
计算单链表长度:
// 计算单链表的长度
int Length(LinkList L){
int len=0; //统计表长
LNode *p = L;
while(p->next != NULL){
p = p->next;
len++;
}
return len;
}
时间复杂度: O ( n ) O(n) O(n)
2.3.6. 单链表的建立
尾插法建立单链表:
// 使用尾插法建立单链表L
LinkList List_TailInsert(LinkList &L){
int x; //设ElemType为整型int
L = (LinkList)malloc(sizeof(LNode)); //建立头结点(初始化空表)
LNode *s, *r = L; //r为表尾指针
scanf("%d", &x); //输入要插入的结点的值
while(x!=9999){ //输入9999表示结束
s = (LNode *)malloc(sizeof(LNode));
s->data = x;
r->next = s;
r = s; //r指针指向新的表尾结点
scanf("%d", &x);
}
r->next = NULL; //尾结点指针置空
return L;
}
时间复杂度: O ( n ) O(n) O(n)
头插法建立单链表:
LinkList List_HeadInsert(LinkList &L){ //逆向建立单链表
LNode *s;
int x;
L = (LinkList)malloc(sizeof(LNode)); //建立头结点
L->next = NULL; //初始为空链表,这步很关键
scanf("%d", &x); //输入要插入的结点的值
while(x!=9999){ //输入9999表结束
s = (LNode *)malloc(sizeof(LNode));
s->data = x;
s->next = L->next;
L->next = s;
//将新结点插入表中,L为头指针
scanf("%d", &x);
}
return L;
}
头插法实现链表的逆置:
// 将链表L中的数据逆置并返回
LNode *Inverse(LNode *L){
LNode *p, *q;
p = L->next; //p指针指向第一个结点
L->next = NULL; //头结点置空
// 依次判断p结点中的数据并采用头插法插到L链表中
while (p != NULL){
q = p;
p = p->next;
q->next = L->next;
L->next = q;
}
return L;
}
具体解释详见【数据结构】单链表逆置:头插法图解
2.3.7. 双链表

-
**双链表的定义:**双链表也是链表的一种。双链表的每个数据节点中都有两个指针,分别指向前驱节点和后继结点。
-
双链表的实现:
typedef struct DNode{ //定义双链表结点类型 ElemType data; //数据域 struct DNode *prior, *next; //前驱和后继指针 }DNode, *DLinklist; -
双链表的初始化 (带头结点):
typedef struct DNode{ ElemType data; struct DNode *prior, *next; }DNode, *DLinklist; // 初始化双链表 bool InitDLinkList(Dlinklist &L){ L = (DNode *)malloc(sizeof(DNode)); if(L==NULL) return false; L->prior = NULL; //头结点的prior指针永远指向NULL L->next = NULL; //头结点之后暂时还没有结点,置空 return true; } void testDLinkList(){ DLinklist L; InitDLinkList(L); ... } // 判断双链表是否为空 bool Empty(DLinklist L){ if(L->next == NULL) return true; else return false; } -
双链表的后插操作:
typedef struct DNode{ ElemType data; struct DNode *prior, *next; }DNode, *DLinklist; // 将结点s插入到结点p之后 bool InsertNextDNode(DNode *p, DNode *s){ if(p==NULL || s==NULL) return false; s->next = p->next; // 判断结点p之后是否有后继结点 if (p->next != NULL) p->next->prior = s; s->prior = p; p->next = s; return true; }
双链表的前插操作、按位序插入操作都可以转换成后插操作
-
双链表的删除操作:
// 删除p结点的后继结点 bool DeletNextDNode(DNode *p){ if(p==NULL) return false; // 找到p的后继结点q DNode *q =p->next; if(q==NULL) return false; p->next = q->next; if(q->next != NULL) q->next->prior=p; free(q); return true; } // 销毁一个双链表 bool DestoryList(DLinklist &L){ // 循环释放各个数据结点 while(L->next != NULL){ DeletNextDNode(L); free(L); // 头指针置空 L=NULL; } } -
双链表的遍历:
// 向后遍历 while(p!=NULL){ // 对结点p做相应处理 p = p->next; } // 向前遍历 while(p!=NULL){ // 对结点p做相应处理 p = p->prior; } // 跳过头结点的遍历 while(p->prior!=NULL){ //对结点p做相应处理 p = p->prior; }
双链表不可随机存取,按位查找、按值查找操作都只能用遍历的方式实现。
2.3.8. 循环链表


-
**循环链表的定义:**循环链表是另一种形式的链式存储结构。它的特点是表中最后一个结点的指针域指向头结点,整个链表形成一个环。
-
循环单链表的实现:
typedef struct LNode{ ElemType data; struct LNode *next; }DNode, *Linklist; // 初始化循环单链表 bool InitList(LinkList &L){ L = (LNode *)malloc(sizeof(LNode)); if(L==NULL) return false; // 最后一个结点的next指针指向头结点 L->next = L; return true; } // 判断循环单链表是否为空 bool Empty(LinkList L){ if(L->next == L) return true; else return false; } // 判断结点p是否为循环单链表的表尾结点 bool isTail(LinkList L, LNode *p){ if(p->next == L) return true; else return false; } -
循环双链表的实现:
typedef struct DNode{ ElemType data; struct DNode *prior, *next; }DNode, *DLinklist; // 初始循环双链表 bool InitDLinkList(DLinklist &L){ L = (DNode *) malloc(sizeof(DNode)); if(L==NULL) return false; // 头结点的prior指针指向最后一个结点,最后一个结点的next指针指向头结点 L->prior = L; L->next = L; } // 判断循环双链表是否为空 bool Empty(DLinklist L){ if(L->next == L) return true; else return false; } // 判断结点p是否为循环双链表的表尾结点 bool isTail(DLinklist L, DNode *p){ if(p->next == L) return true; else return false; } -
循环双链表的插入和删除操作:
// 将结点s插入到结点p之后 bool InsertNextDNode(DNode *p, DNode *s){ s->next = p->next; //循环双链表不用担心p结点的下一个结点为空 p->next->prior = s; s->prior = p; p->next = s; } // 删除p结点的后继结点 bool DeletNextDNode(DNode *p){ // 找到p的后继结点q DNode *q =p->next; //循环双链表不用担心q结点的下一个结点为空 p->next = q->next; q->next->prior=p; free(q); return true; }
2.3.9. 静态链表
- 静态链表的定义:用数组的方式实现的链表。分配一整片连续的内存空间,各个结点集中安置,每个结点包括了数据元素和下一个结点的数组下标。

-
特点:
- 优点:增、删操作不需要大量移动元素。
- 缺点:不能随机存取,只能从头结点开始依次往后查找,容量固定不变!
-
静态链表的定义:
#define MaxSize 10 //静态链表的最大长度 struct Node{ //静态链表结构类型的定义 ElemType data; //存储数据元素 int next; //下一个元素的数组下标 }; // 用数组定义多个连续存放的结点 void testSLinkList(){ struct Node a[MaxSize]; //数组a作为静态链表, 每一个数组元素的类型都是struct Node ... }也可以这么定义:
#define MaxSize 10 //静态链表的最大长度 typedef struct{ //静态链表结构类型的定义 ELemType data; //存储数据元素 int next; //下一个元素的数组下标 }SLinkList[MaxSize]; void testSLinkList(){ SLinkList a; }第一种是我们更加熟悉的写法,第二种写法则更加侧重于强调 a 是一个静态链表而非数组。
-
静态链表的注意点:
- 初始化静态链表时,需要把
a[0]的next设为-1,并将空闲结点的next设置为某个特殊值,比如-2。 - 按位序查找结点时,从头结点出发挨个往后遍历结点,时间复杂度 O = ( n ) O=(n) O=(n)。
- 按位序插入结点的步骤:①找到一个空的结点,存入数据元素;②从头结点出发找到位序为 i-1 的结点;③修改新结点的
next为 -1;④修改 i-1 号结点的next为新结点的下标;
- 初始化静态链表时,需要把
2.3.10. 顺序表和链表的比较
-
逻辑结构:顺序表和链表都属于线性表,都是线性结构。
-
存储结构:
-
顺序表:顺序存储
- 优点:支持随机存取,存储密度高。
- 缺点:大片连续空间分配不方便,改变容量不方便。
-
链表:链式存储
- 优点:离散的小空间分配方便,改变容量方便。
- 缺点:不可随机存取,存储密度低。
-
-
基本操作 - 创建:
-
顺序表:需要预分配大片连续空间。若分配空间过小,则之后不方便拓展容量;若分配空间过大,则浪费内存资源。
- 静态分配:静态数组,容量不可改变。
- 动态分配:动态数组,容量可以改变,但是需要移动大量元素,时间代价高(使用
malloc()、free())。
-
链表:只需要分配一个头结点或者只声明一个头指针。
-
-
基本操作 - 销毁:
-
顺序表:修改
Length= 0- 静态分配:静态数组——系统自动回收空间。
- 动态分配:动态数组——需要手动
free()。
-
链表:依次删除各个结点
free()。
-
-
基本操作 - 增/删:
- 顺序表:插入 / 删除元素要将后续元素后移 / 前移;时间复杂度: O ( n ) O(n) O(n),时间开销主要来自于移动元素。
- 链表:插入 / 删除元素只需要修改指针;时间复杂度: O ( n ) O(n) O(n),时间开销主要来自查找目标元素。
-
基本操作 - 查找:
- 顺序表
- 按位查找: O ( 1 ) O(1) O(1)
- 按值查找: O ( n ) O(n) O(n),若表内元素有序,可在 O ( l o g 2 n ) O(log2n) O(log2n) 时间内找到(二分法)
- 链表:
- 按位查找: O ( n ) O(n) O(n)
- 按值查找: O ( n ) O(n) O(n)
- 顺序表
三、栈与队列
3.1. 栈
3.1.1. 栈的基本概念
- 栈是特殊的线性表:只允许在一端进行插入或删除操作,其逻辑结构与普通线性表相同。
- 栈顶:允许进行插入和删除的一端 (最上面的为栈顶元素)。
- 栈底:不允许进行插入和删除的一端 (最下面的为栈底元素)。
- 空栈:不含任何元素的空表。
- 特点:后进先出(后进栈的元素先出栈)、LIFO(Last In First Out)。
- 缺点:栈的大小不可变,解决方法:共享栈。

3.1.2. 栈的基本操作
-
InitStack(&S):初始化栈。构造一个空栈 S,分配内存空间。 -
DestroyStack(&S):销毁栈。销毁并释放栈 S 所占用的内存空间。 -
Push(&S, x):进栈。若栈 S 未满,则将 x 加入使其成为新的栈顶元素。 -
Pop(&S, &x):出栈。若栈 S 非空,则弹出(删除)栈顶元素,并用 x 返回。 -
GetTop(S, &x):读取栈顶元素。若栈 S 非空,则用 x 返回栈顶元素。 -
StackEmpty(S):判空。断一个栈 S 是否为空,若 S 为空,则返回 true,否则返回 false。
3.1.3. 栈的顺序存储实现
顺序栈的定义:
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶元素
}SqStack;
void testStack(){
SqStack S; //声明一个顺序栈(分配空间)
}
顺序栈的初始化:
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int top;
}SqStack;
// 初始化栈
void InitStack(SqStack &S){
S.top = -1; //初始化栈顶指针
}
// 判断栈是否为空
bool StackEmpty(SqStack S){
if(S.top == -1)
return true;
else
return false;
}
入栈出栈:
// 新元素进栈
bool Push(SqStack &S, ElemType x){ // 判断栈是否已满
if(S.top == MaxSize - 1)
return false;
S.data[++S.top] = x;
return true;
}
// 出栈
bool Pop(SqStack &x, ElemType &x){ // 判断栈是否为空
if(S.top == -1)
return false;
x = S.data[S.top--];
return true;
}
读取栈顶元素:
// 读栈顶元素
bool GetTop(SqStack S, ElemType &x){
if(S.top == -1)
return false;
x = S.data[S.top];
return true;
}
共享栈(两个栈共享同一片空间):
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top0; //0号栈栈顶指针
int top1; //1号栈栈顶指针
}ShStack;
// 初始化栈
void InitSqStack(ShStack &S){
S.top0 = -1;
S.top1 = MaxSize;
}
3.1.4. 栈的链式存储实现
链栈的定义:
typedef struct Linknode{
ElemType data; //数据域
Linknode *next; //指针域
}Linknode,*LiStack;
void testStack(){
LiStack L; //声明一个链栈
}
链栈的初始化:
typedef struct Linknode{
ElemType data;
Linknode *next;
}Linknode,*LiStack;
// 初始化栈
bool InitStack(LiStack &L){
L = (Linknode *)malloc(sizeof(Linknode));
if(L == NULL)
return false;
L->next = NULL;
return true;
}
// 判断栈是否为空
bool isEmpty(LiStack &L){
if(L->next == NULL)
return true;
else
return false;
}
入栈出栈:
// 新元素入栈
bool pushStack(LiStack &L,ElemType x){
Linknode *s = (Linknode *)malloc(sizeof(Linknode));
if(s == NULL)
return false;
s->data = x;
// 头插法
s->next = L->next;
L->next = s;
return true;
}
// 出栈
bool popStack(LiStack &L, int &x){
// 栈空不能出栈
if(L->next == NULL)
return false;
Linknode *s = L->next;
x = s->data;
L->next = s->next;
free(s);
return true;
}
3.2. 队列
3.2.1. 队列的基本概念
- 队列是操作受限的线性表:只允许在一端进行插入 (入队),另一端进行删除 (出队)。
- 队头:允许删除的一端。
- 队尾:允许插入的一端。
- 空队列:不含任何元素的空表。
- 特点:先进先出(先入队的元素先出队)、FIFO(First In First Out)。

3.2.2. 队列的基本操作
-
InitQueue(&Q):初始化队列。构造一个空队列 Q。 -
DestroyQueue(&Q):销毁队列。销毁并释放队列 Q 所占用的内存空间。 -
EnQueue(&Q, x):入队。若队列 Q 未满,将 x 加入,使之成为新的队尾。 -
DeQueue(&Q, &x):出队。若队列 Q 非空,删除队头元素,并用 x 返回。 -
GetHead(Q,&x):读队头元素。若队列 Q 非空,则将队头元素赋值给 x。 -
QueueEmpty(Q):判空。若队列 Q 为空,则返回 true。
3.2.3. 队列的顺序存储实现
顺序队列的定义:
#define MaxSize 10; //定义队列中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //用静态数组存放队列元素
int front, rear; //队头指针和队尾指针
}SqQueue;
void test{
SqQueue Q; //声明一个队列
}
顺序队列的初始化:
#define MaxSize 10;
typedef struct{
ElemType data[MaxSize];
int front, rear;
}SqQueue;
// 初始化队列
void InitQueue(SqQueue &Q){
// 初始化时,队头、队尾指针指向0
// 队尾指针指向的是即将插入数据的数组下标
// 队头指针指向的是队头元素的数组下标
Q.rear = Q.front = 0;
}
// 判断队列是否为空
bool QueueEmpty(SqQueue Q){
if(Q.rear == Q.front)
return true;
else
return false;
}
入队出队(循环队列):
// 新元素入队
bool EnQueue(SqQueue &Q, ElemType x){
// 如果队列已满直接返回
if((Q.rear+1)%MaxSize == Q.front) //牺牲一个单元区分队空和队满
return false;
Q.data[Q.rear] = x;
Q.rear = (Q.rear+1)%MaxSize;
return true;
}
// 出队
bool DeQueue(SqQueue &Q, ElemType &x){
// 如果队列为空直接返回
if(Q.rear == Q.front)
return false;
x = Q.data[Q.front];
Q.front = (Q.front+1)%MaxSize;
return true;
}
获得队头元素:
// 获取队头元素并存入x
bool GetHead(SqQueue &Q, ElemType &x){
if(Q.rear == Q.front)
return false;
x = Q.data[Q.front];
return true;
}
注意:
-
循环队列不能使用
Q.rear == Q.front作为判空的条件,因为当队列已满时也符合该条件,会与判空发生冲突! -
解决方法一:牺牲一个单元来区分队空和队满,即将
(Q.rear+1)%MaxSize == Q.front作为判断队列是否已满的条件。(主流方法) -
解决方法二:设置 size 变量记录队列长度。
#define MaxSize 10; typedef struct{ ElemType data[MaxSize]; int front, rear; int size; }SqQueue; // 初始化队列 void InitQueue(SqQueue &Q){ Q.rear = Q.front = 0; Q.size = 0; } // 判断队列是否为空 bool QueueEmpty(SqQueue 0){ if(Q.size == 0) return true; else return false; } // 新元素入队 bool EnQueue(SqQueue &Q, ElemType x){ if(Q.size == MaxSize) return false; Q.size++; Q.data[Q.rear] = x; Q.rear = (Q.rear+1)%MaxSize; return true; } // 出队 bool DeQueue(SqQueue &Q, ElemType &x){ if(Q.size == 0) return false; Q.size--; x = Q.data[Q.front]; Q.front = (Q.front+1)%MaxSize; return true; } -
解决方法三:设置 tag 变量记录队列最近的操作。(
tag=0:最近进行的是删除操作;tag=1:最近进行的是插入操作)#define MaxSize 10; typedef struct{ ElemType data[MaxSize]; int front, rear; int tag; }SqQueue; // 初始化队列 void InitQueue(SqQueue &Q){ Q.rear = Q.front = 0; Q.tag = 0; } // 判断队列是否为空 bool QueueEmpty(SqQueue 0){ if(Q.front == Q.rear && Q.tag == 0) return true; else return false; } // 新元素入队 bool EnQueue(SqQueue &Q, ElemType x){ if(Q.rear == Q.front && tag == 1) return false; Q.data[Q.rear] = x; Q.rear = (Q.rear+1)%MaxSize; Q.tag = 1; return true; } // 出队 bool DeQueue(SqQueue &Q, ElemType &x){ if(Q.rear == Q.front && tag == 0) return false; x = Q.data[Q.front]; Q.front = (Q.front+1)%MaxSize; Q.tag = 0; return true; }
3.2.4. 队列的链式存储实现
链队列的定义:
// 链式队列结点
typedef struct LinkNode{
ElemType data;
struct LinkNode *next;
}
// 链式队列
typedef struct{
// 头指针和尾指针
LinkNode *front, *rear;
}LinkQueue;
链队列的初始化(带头结点):

typedef struct LinkNode{
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{
LinkNode *front, *rear;
}LinkQueue;
// 初始化队列
void InitQueue(LinkQueue &Q){
// 初始化时,front、rear都指向头结点
Q.front = Q.rear = (LinkNode *)malloc(sizeof(LinkNode));
Q.front -> next = NULL;
}
// 判断队列是否为空
bool IsEmpty(LinkQueue Q){
if(Q.front == Q.rear)
return true;
else
return false;
}
入队出队:
// 新元素入队
void EnQueue(LinkQueue &Q, ElemType x){
LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
Q.rear->next = s;
Q.rear = s;
}
// 队头元素出队
bool DeQueue(LinkQueue &Q, ElemType &x){
if(Q.front == Q.rear)
return false;
LinkNode *p = Q.front->next;
x = p->data;
Q.front->next = p->next;
// 如果p是最后一个结点,则将队头指针也指向NULL
if(Q.rear == p)
Q.rear = Q.front;
free(p);
return true;
}
以上是带头结点的链队列,下面是不带头结点的操作:
typedef struct LinkNode{
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{
LinkNode *front, *rear;
}LinkQueue;
// 初始化队列
void InitQueue(LinkQueue &Q){
// 不带头结点的链队列初始化,头指针和尾指针都指向NULL
Q.front = NULL;
Q.rear = NULL;
}
// 判断队列是否为空
bool IsEmpty(LinkQueue Q){
if(Q.front == NULL)
return true;
else
return false;
}
// 新元素入队
void EnQueue(LinkQueue &Q, ElemType x){
LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
// 第一个元素入队时需要特别处理
if(Q.front == NULL){
Q.front = s;
Q.rear = s;
}else{
Q.rear->next = s;
Q.rear = s;
}
}
//队头元素出队
bool DeQueue(LinkQueue &Q, ElemType &x){
if(Q.front == NULL)
return false;
LinkNode *s = Q.front;
x = s->data;
if(Q.front == Q.rear){
Q.front = Q.rear = NULL;
}else{
Q.front = Q.front->next;
}
free(s);
return true;
}
3.2.5. 双端队列
-
定义:
- 双端队列是允许从两端插入、两端删除的线性表。
- 如果只使用其中一端的插入、删除操作,则等同于栈。
- 输入受限的双端队列:允许一端插入,两端删除的线性表。
- 输出受限的双端队列:允许两端插入,一端删除的线性表。
-
考点:判断输出序列的合法化
- 例:数据元素输入序列为 1,2,3,4,判断 4! = 24 个输出序列的合法性
栈中合法的序列,双端队列中一定也合法ZS
| 栈 | 输入受限的双端队列 | 输出受限的双端队列 |
|---|---|---|
| 14个合法 ( 1 n + 1 C 2 n n \frac{1}{n+1}C^{n}_{2n} n+11C2nn) | 只有 4213 和 4231 不合法 | 只有 4132 和 4231 不合法 |
3.3. 栈与队列的应用
3.3.1 栈在括号匹配中的应用
- 用栈实现括号匹配:
- 最后出现的左括号最先被匹配 (栈的特性——LIFO)。
- 遇到左括号就入栈。
- 遇到右括号,就“消耗”一个左括号(出栈)。
- 匹配失败情况:
- 扫描到右括号且栈空,则该右括号单身。
- 扫描完所有括号后,栈非空,则该左括号单身。
- 左右括号不匹配。
#define MaxSize 10
typedef struct{
char data[MaxSize];
int top;
}SqStack;
void InitStack(SqStack &S);
bool StackEmpty(SqStack &S);
bool Push(SqStack &S, char x);
bool Pop(SqStack &S, char &x);
// 判断长度为length的字符串str中的括号是否匹配
bool bracketCheck(char str[], int length){
SqStack S;
InitStack(S);
// 遍历str
for(int i=0; i<length; i++){
// 扫描到左括号,入栈
if(str[i] == '(' || str[i] == '[' || str[i] == '{'){
Push(S, str[i]);
}else{
// 扫描到右括号且栈空直接返回
if(StackEmpty(S))
return false;
char topElem;
// 用topElem接收栈顶元素
Pop(S, topElem);
// 括号不匹配
if(str[i] == ')' && topElem != '(' )
return false;
if(str[i] == ']' && topElem != '[' )
return false;
if(str[i] == '}' && topElem != '{' )
return false; }
}
// 扫描完毕若栈空则说明字符串str中括号匹配
return StackEmpty(S);
}
3.3.2. 栈在表达式求值中的应用
- 中缀表达式:中缀表达式是一种通用的算术或逻辑公式表示方法,运算符以中缀形式处于操作数的中间。对于计算机来说中缀表达式是很复杂的,因此计算表达式的值时,通常需要先将中缀表达式转换为前缀或后缀表达式,然后再进行求值。
- 前缀表达式(波兰表达式):前缀表达式的运算符位于两个操作数之前。
- 后缀表达式(逆波兰表达式):后缀表达式的运算符位于两个操作数之后。
-
中缀转后缀的手算方法:
- 确定中缀表达式中各个运算符的运算顺序。
- 选择下一个运算符,按照==「左操作数 右操作数 运算符」==的方式组合成一个新的操作数。
- 如果还有运算符没被处理,就继续执行。
-
例:将 ( ( 15 ÷ ( 7 − ( 1 + 1 ) ) ) × 3 ) − ( 2 + ( 1 + 1 ) ) ((15÷(7−(1+1)))×3)−(2+(1+1)) ((15÷(7−(1+1)))×3)−(2+(1+1)) 转换为后缀表达式?
答: 15 7 1 1 + − ÷ 3 × 2 1 1 + + − 15\ 7\ 1\ 1 + -\ ÷\ 3\ ×\ 2\ 1\ 1\ + +\ - 15 7 1 1+− ÷ 3 × 2 1 1 ++ −
中缀转后缀要遵循“左优先”原则:只要左边的运算符能先计算,就优先计算左边的。
- **后缀表达式的手算方法:**从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算, 合体为一个操作数。
-
例:计算 A B C D − × + E F ÷ − A\ B\ C\ D - × + E\ F\ ÷\ - A B C D−×+E F ÷ − ?
答: ( A + B × ( C − D ) ) − E ÷ F (A+B×(C-D))-E÷F (A+B×(C−D))−E÷F
-
后缀表达式的机算方法:
- 从左往右扫描下一个元素,直到处理完所有元素。
- 若扫描到操作数则压入栈,并回到第一步;否则执行第三步。
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到第一步。
弹出栈顶元素时,先出栈的是“右操作数”。
-
中缀转前缀的手算方法:
- 确定中缀表达式中各个运算符的运算顺序。
- 选择下一个运算符,按照==「运算符 左操作数 右操作数」==的方式组合成一个新的操作数。
- 如果还有运算符没被处理,就继续执行第二步。
-
例:将 A + B ∗ ( C − D ) – E / F A + B * (C - D) – E / F A+B∗(C−D)–E/F 转为前缀表达式?
答: + A − ∗ B − C D / E F +\ A - *\ B - C\ D\ /\ E\ F + A−∗ B−C D / E F
中缀转前缀遵循“右优先”原则:只要右边的运算符能先计算,就优先算右边的。
-
前缀表达式的计算方法:
- 从右往左扫描下一个元素,直到处理完所有元素。
- 若扫描到操作数则压入栈,并回到第一步;否则执行第三步。
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到第一步。
-
**中缀转后缀的机算方法:**初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
- 遇到操作数:直接加入后缀表达式。
- 遇到界限符:遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到 弹出“(”为止。注意:“(”不加入后缀表达式。
- 遇到运算符:依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式, 若碰到“(” 或栈空则停止。之后再把当前运算符入栈。
#define MaxSize 40 typedef struct{ char data[MaxSize]; int top; }SqStack; typedef struct{ char data[MaxSize]; int front,rear; }SqQueue; void InitStack(SqStack &S); bool StackEmpty(SqStack S); bool Push(SqStack &S, char x); bool Pop(SqStack &S, char &x); void InitQueue(SqQueue &Q); bool EnQueue(LQueue &Q, char x); bool DeQueue(LQueue &Q, char &x); bool QueueEmpty(SqQueue Q); // 判断元素ch是否入栈 int JudgeEnStack(SqStack &S, char ch){ char tp = S.data[S->top]; // 如果ch是a~z则返回-1 if(ch >= 'a' && ch <= 'z') return -1; // 如果ch是+、-、*、/且栈顶元素优先级大于等于ch则返回0 else if(ch == '+' && (tp == '+' || tp == '-' || tp == '*' || tp == '/')) return 0; else if(ch == '-' && (tp == '+' || tp == '-' || tp == '*' || tp == '/')) return 0; else if(ch == '*' && (tp == '*' || tp == '/')) return 0; else if(ch == '/' && (tp == '*' || tp == '/')) return 0; // 如果ch是右括号则返回2 else if(ch == ')') return 2; // 其他情况ch入栈,返回1 else return 1; } // 中缀表达式转后缀表达式 int main(int argc, char const *argv[]) { SqStack S; SqQueue Q; InitStack(S); InitQueue(Q); char ch; printf("请输入表达式,以“#”结束:"); scanf("%c", &ch); while (ch != '#'){ // 当栈为空时 if(StackEmpty(&S)){ // 如果输入的是数即a~z,直接入队 if(ch >= 'a' && ch <= 'z') EnQueue(Q, ch); // 如果输入的是运算符,直接入栈 else Puch(S, ch); }else{ // 当栈非空时,判断ch是否需要入栈 int n = JudgeEnStack(S, ch); // 当输入是数字时直接入队 if(n == -1){ EnQueue(Q, ch); }else if(n == 0){ // 当输入是运算符且运算符优先级不高于栈顶元素时 while (1){ // 取栈顶元素入队 char tp; Pop(S, tp); EnQueue(Q, tp); // 再次判断是否需要入栈 n = JudgeEnStack(S, ch); // 当栈头优先级低于输入运算符或者栈头为‘)’时,入栈并跳出循环 if(n != 0){ EnStack(S, ch); break; } } }else if(n == 2){ // 当出现‘)’时 将()中间的运算符全部出栈入队 while(1){ char tp; Pop(S, tp); if(tp == '(') break; else EnQueue(Q, tp); } }else{ // 当运算符优先级高于栈顶元素或出现‘(’时直接入栈 Push(S, ch); } } scanf("%c", &ch); } // 将最后栈中剩余的运算符出栈入队 while (!StackEmpty(S)){ char tp; Pop(S, tp); EnQueue(Q, tp); } // 输出队中元素 while (!QueueEmpety(Q)){ printf("%c ", DeQueue(Q)); } return 0; } -
**中缀表达式的机算方法:**中缀转后缀 + 后缀表达式的求值(两个算法的结合)
- 初始化两个栈,(操作数栈和运算符栈),若扫描到操作数,压入操作数栈;若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算, 运算结果再压回操作数栈)。
3.3.3. 栈在递归中的应用
-
函数调用的特点:最后被调用的函数最先执行结束(LIFO)。
-
函数调用时,需要用一个“函数调用栈” 存储:
- 调用返回地址
- 实参
- 局部变量
-
递归调用时,函数调用栈可称为“递归工作栈” 。每进入一层递归,就将递归调用所需信息压入栈顶;每退出一层递归,就从栈顶弹出相应信息。
-
缺点:效率低,太多层递归可能会导致栈溢出;可能包含很多重复计算。
-
可以自定义栈将递归算法改造成非递归算法。
3.3.4. 队列的应用
- 树的层次遍历
- 图的广度优先遍历
- 操作系统中多个进程争抢着使用有限的系统资源时,先来先服务算法(First Come First Service)是是一种常用策略。
3.4. 特殊矩阵的压缩存储
除非题目特别说明,否则数组下标默认从0开始。
-
一维数组的存储:各数组元素大小相同,且物理上连续存放。设起始地址为 LOC,则数组元素 a [ i ] a[i] a[i] 的存放地址 = LOC + i * sizeof(ElemType) (0≤i<10)
-
二维数组的存储:
-
M 行 N 列的二维数组 b [ M ] [ N ] b[M][N] b[M][N] 中,设起始地址为 LOC,若按行优先存储,则 b [ i ] [ j ] b[i][j] b[i][j] 的存储地址 = LOC + (i*N + j) * sizeof(ElemType)

-
M 行 N 列的二维数组 b [ M ] [ N ] b[M][N] b[M][N] 中,设起始地址为 LOC,若按列优先存储,则 b [ i ] [ j ] b[i][j] b[i][j] 的存储地址 = LOC + (j*M + i) * sizeof(ElemType)

-
-
**对称矩阵的压缩存储:**若 n 阶矩阵中任意一个元素 a i , j a_{i,j} ai,j都有 a i , j = a j , i a_{i,j} = a_{j,i} ai,j=aj,i 则该矩阵为对称矩阵。对于对称矩阵,只需存储主对角线+下三角区。若按照行优先原则将各元素存入一维数组中,即 a i , j a_{i,j} ai,j 存入到数组 B [ k ] B[k] B[k] 中,那么有 k = j ( j − 1 ) 2 + i − 1 k=\frac{j(j-1)}{2}+i-1 k=2j(j−1)+i−1 ,又 a i , j = a j , i a_{i,j}=a_{j,i} ai,j=aj,i 故有:
k = { i ( i − 1 ) 2 + j − 1 , i ≥ j j ( j − 1 ) 2 + i − 1 , i < j k=\left\{ \begin{array}{lr} \frac{i(i-1)}{2}+j-1, &i\geq j&\\ \frac{j(j-1)}{2}+i-1, &i< j&\\ \end{array} \right. k={2i(i−1)+j−1,2j(j−1)+i−1,i≥ji<j

-
三角矩阵的压缩存储:
-
下三角矩阵:除了主对角线和下三角区,其余的元素都相同。
-
上三角矩阵:除了主对角线和上三角区,其余的元素都相同。
-
压缩存储策略:按行优先原则将主对角线+下三角区存入一维数组中,并在最后一个位置存储常量。即 a i , j a_{i,j} ai,j 存入到数组 B [ k ] B[k] B[k] 中,那么数组 B [ k ] B[k] B[k] 共有 n ( n − 1 ) 2 + 1 \frac{n(n-1)}{2}+1 2n(n−1)+1 个元素。对于k,有:
k = { i ( i − 1 ) 2 + j − 1 , i ≥ j n ( n − 1 ) 2 , i < j k=\left\{ \begin{array}{lr} \frac{i(i-1)}{2}+j-1, &i\geq j&\\ \frac{n(n-1)}{2}, &i< j&\\ \end{array} \right. k={2i(i−1)+j−1,2n(n−1),i≥ji<j
-

- **三对角矩阵的压缩存储:**三对角矩阵,又称带状矩阵:当 ∣ i − j ∣ > 1 |i - j|>1 ∣i−j∣>1 时,有 a i , j = 0 ( 1 ≤ i , j ≤ n ) a_{i,j} = 0 (1≤i,j ≤n) ai,j=0(1≤i,j≤n)。对于三对角矩阵,按行优先原则,只存储带状部分,即 a i , j a_{i,j} ai,j 存入到数组 B [ k ] B[k] B[k] 中,那么 k = 2 i + j − 3 k = 2i+j-3 k=2i+j−3。若已知数组下标 k,则 i = ⌊ ( k + 1 ) / 3 + 1 ⌋ i=\lfloor (k+1)/3+1\rfloor i=⌊(k+1)/3+1⌋。

- **稀疏矩阵的压缩存储:**稀疏矩阵的非零元素远远少于矩阵元素的个数。压缩存储策略:
- 顺序存储:三元组 <行,列,值>
- 链式存储:十字链表法


四、串
4.1. 串的基本概念
- 串:即字符串(String)是由零个或多个字符组成的有限序列。
- 串的长度:中字符的个数 n, n = 0 n = 0 n=0 时的串称为空串。
- 子串:串中任意个连续的字符组成的子序列。
- 主串:包含子串的串。
- 字符在主串中的位置:字符在串中的序号。
- 子串在主串中的位置:子串的第一个字符在主串中的位置 。
4.2. 串的基本操作
-
StrAssign(&T, chars):赋值操作。把串 T 赋值为 chars。 -
StrCopy(&T, S):复制操作。由串 S 复制得到串 T。 -
StrEmpty(S):判空操作。若 S 为空串,则返回 TRUE,否则返回 FALSE。 -
StrLength(S):求串长。返回串 S 中元素的个数。 -
ClearString(&S):清空操作。将 S 清为空串。 -
DestroyString(&S):销毁串。将串 S 销毁(回收存储空间)。 -
Concat(&T, S1, S2):串联接。用 T 返回由 S1 和 S2 联接而成的新串 。 -
SubString(&Sub, S, pos, len):求子串。用 Sub 返回串 S 的第 pos 个字符起长度为 len 的子串。 -
Index(S, T):定位操作。若主串 S 中存在与串 T 值相同的子串,则返回它在主串 S 中第一次出现的位置;否则函数值为 0。 -
StrCompare(S, T):比较操作。若 S>T,则返回值>0;若 S=T,则返回值=0;若 S<T,则返回值<0。
4.3. 串的存储实现
串的顺序存储(静态数组):
// ch[0]废弃不用,声明int型变量length来存放串的长度
#define MAXLEN 255
typedef struct{
char ch[MAXLEN];
int length;
}SString;
// 串的初始化
bool InitString(SString &S){
S.length = 0;
return true;
}
// 求串的长度
int StrLength(SString S){
return S.length;
}
// 求主串由位序pos开始len长度的子串存入到串Sub中
bool SubString(SString &Sub, SString S, int pos, int len){
if(pos+len-1 > S.length)
return false;
for(int i=pos; i<pos+len; i++)
Sub.ch[i-pos+1] = S.ch[i];
Sub.length = len;
return true;
}
// 比较S与T的大小。若S>T,则返回值大于0;若S=T,则返回值等于0;若S<T,则返回值小于0
int StrCompare(SString S, SString T){
for(int i=1; i<=S.length && i<=T.length; i++){
if(S.ch[i]!=T.ch[i])
return S.ch[i]-T.ch[i]
}
// 扫描过的所有字符都相同,则长度长的串更大
return S.length-T.length;
}
// 定位串T在串S中的位置,若无法定位则返回0
int Index(SString S, SString T){
int i=1, n=StrLength(S), m=StrLength(T);
SString sub; //用于暂存数据
while(i<=n-m+1){
SubString(sub, S, i, m);
if(StrCompare(sub, T)!=0)
++i;
else
return i;
}
return 0;
}
void test{
SString S;
InitString(S);
...
}
串的顺序存储(动态数组):
#define MAXLEN 255
typedef struct{
char *ch;
int length;
}HString;
bool InitString(HString &S){
S.ch = (char *)malloc(MAXLEN * sizeof(char));
if(S.ch == NULL)
return false;
S.length = 0;
return true;
}
void test{
HString S;
InitString(S);
...
}
串的链式存储:
typedef struct StringNode{
char ch; //每个结点存1个字符
struct StringNode *next;
}StringNode, *String;
上述方式存储密度很低,可以使每个结点存储多个字符。每个结点被称为块,整个链表被称为块链结构。
typedef struct StringNode{
char ch[4]; //每个结点存多个字符
struct StringNode *next;
}StringNode, *String;
4.4. 串的朴素模式匹配
- 串的模式匹配:在主串中找到与模式串相同的子串,并返回其所在主串中的位置。
- 朴素模式匹配算法思想:将主串中与模式串长度相同的子串搞出来,挨个与模式串对比。当子串与模式串某个对应字符不匹配时,就立即放弃当前子串,转而检索下一个子串。
- 串的朴素模式匹配算法代码实现:
// 在主串S中找到与模式串T相同的子串并返回其位序,否则返回0
int Index(SString S, SString T){
int k=1;
int i=k, j=1;
while(i<=S.length && j<=T.length){
if(S.ch[i] == T.ch[j]){
++i; ++j;
}else{
k++; i=k; j=1;
}
}
if(j>T.length)
return k;
else
return 0;
}
时间复杂度:设模式串长度为m,主串长度为n
- 匹配成功的最好时间复杂度: O ( m ) O(m) O(m)
- 匹配失败的最好时间复杂度: O ( n ) O(n) O(n)
- 最坏时间复杂度: O ( n m ) O(nm) O(nm)
4.5. KPM算法
- 朴素模式匹配算法的缺点:当某些子串与模式串能部分匹配时,主串的扫描指针 i 经常回溯,导致时间开销增加。最坏时间复杂度 O ( n m ) O(nm) O(nm)。
- 串的前缀:包含第一个字符,且不包含最后一个字符的子串。
- 串的后缀:包含最后一个字符,且不包含第一个字符的子串。
- next 数组的计算方法:当第 j 个字符匹配失败时,将前(1~j-1)个字符组成的串记为S,则:==next[j]=S的最长相等前后缀长度+1。==特别地,next[1]=0。
例:求模式串“abcabd”的 next 数组。
| 序号j | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 模式串 | a | b | c | a | b | d |
| next[j] | 0 | 1 | 1 | 1 | 2 | 3 |
-
KPM 算法:当子串和模式串不匹配时,主串指针 i 不回溯,模式串指针 j=next[j]。KMP 算法的平均时间复杂度为: O ( n + m ) O(n+m) O(n+m)。
-
KPM 算法代码实现:
// 获取模式串T的next[]数组
void getNext(SString T, int next[]){
int i=1, j=0;
next[1]=0;
while(i<T.length){
if(j==0 || T.ch[1]==T.ch[j]){
++i; ++j;
next[i]=j;
}else
j=next[j];
}
}
// KPM算法,求主串S中模式串T的位序,没有则返回0
int Index_KPM(SString S, SString T){
int i=1, j=1;
int next[T.length+1];
getNext(T, next);
while(i<=S.length && j<=T.length){
if(j==0 || S.ch[i]==T.ch[j]){
++i; ++j;
}else
j=next[j];
}
if(j>T.length)
return i-T.length;
else
return 0;
}
int main() {
SString S={"ababcabcd", 9};
SString T={"bcd", 3};
printf("%d ", Index_KPM(S, T)); //输出9
}
- KPM 算法的进一步优化:改进 next 数组:
void getNextval(SString T, int nextval[]){
int i=1,j=0;
nextval[1]=0;
while(i<T.length){
if(j==0 || T.ch[i]==T.ch[j]){
++i; ++j;
if(T.ch[i]!=T.ch[j])
nextval[i]=j;
else
nextval[i]=nextval[j];
}else
j=nextval[j];
}
}
五、树
5.1. 树的概念
5.1.1. 树的定义和基本术语
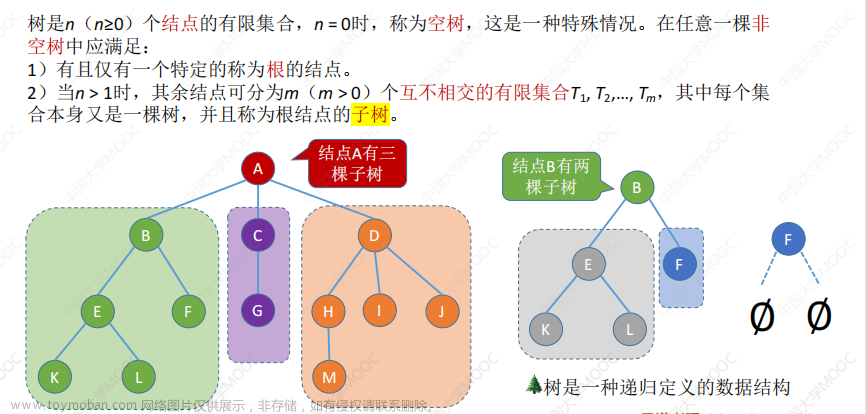
- 树是n(n≥0)个结点的有限集合,n = 0时,称为空树。
- 空树中应满足:
- 有且仅有一个特定的称为根的结点。
- 当n > 1时,其余结点可分为m(m>0)个互不相交的有限集合T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。
- 度:树中一个结点的孩子个数称为该结点的度。所有结点的度的最大值是树的度。
- 度大于0的结点称为分支结点,度为0的结点称为叶子结点。
- 结点的层次(深度):从上往下数。
- 结点的高度:从下往上数。
- 树的高度(深度):树中结点的层数。
- 有序树:逻辑上看,树中结点的各子树从左至右是有次序的,不能互换。
- 若树中结点的各子树从左至右是有次序的,不能互换,则该树称为有序树,否则称为无序树。
- 树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
- 森林:森林是m(m≥0)棵互不相交的树的集合。
5.1.2. 树的常考性质
- 结点数 = 总度数 + 1
- 度为 m 的树、m 叉树的区别:
| 度为m的树 | m叉树的区别 |
|---|---|
| 任意结点的度≤m(最多m个孩子) | 任意结点的度≤m(最多m个孩子) |
| 至少有一个结点度=m(有m个孩子) | 允许所有结点的度都<m |
| 一定是非空树,至少有m+1个结点 | 可以是空树 |
- 度为 m 的树第 i 层至多有 m i − 1 m^{i-1} mi−1 个结点(i≥1);m 叉树第 i 层至多有 m i − 1 m^{i-1} mi−1 个结点(i≥1)。

- 高度为 h 的 m 叉树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1 个结点。(等比数列求和)
- 高度为 h 的 m 叉树至少有 h 个结点;高度为 h、度为 m 的树至少有(h+m-1)个结点。
- 具有 n 个结点的 m 叉树的最小高度为 ⌈ log m ( n ( m − 1 ) + 1 ) ⌉ \lceil \log_{m}(n(m - 1) + 1)\rceil ⌈logm(n(m−1)+1)⌉
5.2. 二叉树
5.2.1. 二叉树的定义
-
二叉树是 n(n≥0)个结点的有限集合:
- 或者为空二叉树,即 n = 0。
- 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成,左子树和右子树又分别是一棵二叉树。
-
二叉树的特点:
- 每个结点至多只有两棵子树。
- 左右子树不能颠倒(二叉树是有序树)。
-
二叉树的五种状态:
- 空二叉树
- 只有左子树
- 只有右子树
- 只有根节点
- 左右子树都有

5.2.2. 特殊二叉树
满二叉树:一棵高度为 h,且含有 2 h − 1 2^h - 1 2h−1 个结点的二叉树。
特点:
- 只有最后一层有叶子结点。
- 不存在度为 1 的结点。
- 若按层序从 1 开始编号,结点 i 的左孩子为 2i,右孩子为 2i+1;结点 i 的父节点为 ⌊ i / 2 ⌋ \lfloor i/2\rfloor ⌊i/2⌋。

完全二叉树:当且仅当其每个结点都与高度为 h 的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。
特点:
- 只有最后两层可能有叶子结点。
- 最多只有一个度为 1 的结点。
- 若按层序从 1 开始编号,结点 i 的左孩子为 2i,右孩子为 2i+1;结点 i 的父节点为 ⌊ i / 2 ⌋ \lfloor i/2\rfloor ⌊i/2⌋。
- i ≤ ⌊ n / 2 ⌋ i≤ \lfloor n/2\rfloor i≤⌊n/2⌋ 为分支结点, i > ⌊ n / 2 ⌋ i> \lfloor n/2\rfloor i>⌊n/2⌋ 为叶子结点。

二叉排序树:一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:左子树上所有结点的关键字均小于根结点的关键字;右子树上所有结点的关键字均大于根结点的关键字。

平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过 1。
5.2.3. 二叉树的性质
-
设非空二叉树中度为 0、1 和 2 的结点个数分别为 n 0 n_0 n0、 n 1 n_1 n1 和 n 2 n_2 n2,则 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
推导过程:设树中结点总数为 n,则: n = n 0 + n 1 + n 2 n=n_0+n_1+n_2 n=n0+n1+n2 , n = n 1 + 2 n 2 + 1 n=n_1+2n_2+1 n=n1+2n2+1。
-
二叉树第 i 层至多有 2 i − 1 2^{i-1} 2i−1 个结点(i≥1)。
-
高度为 h 的二叉树至多有 2 h − 1 2^h − 1 2h−1 个结点(满二叉树)。
-
具有 n 个(n>0)结点的完全二叉树的高度 h 为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n + 1)\rceil ⌈log2(n+1)⌉ 或 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2n\rfloor + 1 ⌊log2n⌋+1。
-
对于完全二叉树,可以由总结点数 n 推出度为 0、1 和 2 的结点个数 n 0 n_0 n0、 n 1 n_1 n1 和 n 2 n_2 n2。
推导过程: n 1 n_1 n1 = 0 或 1, n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1,则 n 0 + n 2 n_0 + n_2 n0+n2 一定是奇数。
若完全二叉树有 2 k 2k 2k(偶数)个结点,则有 n 1 = 1 n_1=1 n1=1, n 0 = k n_0 = k n0=k, n 2 = k − 1 n_2 = k-1 n2=k−1;
若完全二叉树有 2 k − 1 2k-1 2k−1(奇数)个结点,则有 n 1 = 0 n_1=0 n1=0, n 0 = k n_0 = k n0=k, n 2 = k − 1 n_2 = k-1 n2=k−1;
5.2.4. 二叉树的实现
二叉树的顺序存储:
顺序存储完全二叉树:定义一个长度为 MaxSize 的数组 t,按照从上至下、从左至右的顺序依次存储完全二叉树中的各个结点。让第一个位置空缺,保证数组中下标和结点编号一致。
#define MaxSize 100
struct TreeNode{
ElemType value; //结点中的数据元素
bool isEmpty; //结点是否为空
}
//初始化树T
bool initTree(TreeNode T[]){
for(int i=0; i<MaxSize; i++){
T[i].isEmpty=true;
}
return true;
}
void test(){
struct TreeNode T[MaxSize];
initTree(T);
}


这样可以使用二叉树的性质求一些问题:
- 结点 i 的左孩子: 2 i 2i 2i
- 结点 i 的右孩子: 2 i + 1 2i+1 2i+1
- 结点 i 的父节点: ⌊ i / 2 ⌋ \lfloor i/2\rfloor ⌊i/2⌋
- 结点 i 的层次: ⌈ l o g 2 ( i + 1 ) ⌉ \lceil log_2(i + 1)\rceil ⌈log2(i+1)⌉ 或 ⌊ l o g 2 i ⌋ + 1 \lfloor log_2i\rfloor + 1 ⌊log2i⌋+1
但是如果不是完全二叉树,依然按层序将各节点顺序存储,那么将无法从结点编号反映出结点间的逻辑关系。可以将二叉树中的结点编号与完全二叉树对应起来存储,==不过这样会浪费很多内存空间。==因此,二叉树的顺序存储结构,只适合存储完全二叉树。


二叉树的链式存储:
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
//初始化
bool initTree(BiTree &root){
root = (BiTree)malloc(sizeof(BiTNode));
if(root == NULL)
return false;
root->lchild = NULL;
root->rchild = NULL;
return true;
}
void test{
BiTree root = NULL;
initTree(root);
...
}
二叉树的链式存储可以非常方便的找到指定结点的左右孩子,但是找到指定结点的父结点却非常困难,只能从根节点开始遍历寻找。因此,如果寻找父结点的需求比较多,也可以加上父结点指针形成三叉链表。
5.3. 二叉树的遍历和线索二叉树
5.3.1. 二叉树的先中后序遍历
-
遍历:按照某种次序把所有结点都访问一遍。
-
先序遍历(PreOrder)的操作过程:
- 若二叉树为空,则什么也不做;
- 若二叉树非空:
- 访问根结点;
- 先序遍历左子树;
- 先序遍历右子树。
-
中序遍历(InOrder)的操作过程:
-
若二叉树为空,则什么也不做;
-
若二叉树非空:
- 中序遍历左子树;
- 访问根结点;
- 中序遍历右子树。
-
-
后序遍历(PostOrder)的操作过程:
- 若二叉树为空,则什么也不做;
- 若二叉树非空:
- 后序遍历左子树;
- 后序遍历右子树;
- 访问根结点。
-
代码实现:
typedef struct BiTNode{ ElemType data; struct BiTNode *lchild, *rchild; }BiTNode, *BiTree; // 先序遍历 void PreOrder(BiTree T){ if(T!=NULL){ PreOrder(T->lchild); PreOrder(T->rchild); visit(T); } } // 中序遍历 void InOrder(BiTree T){ if(T!=NULL){ InOrder(T->lchild); visit(T); InOrder(T->rchild); } } // 后序遍历 void PostOrder(BiTree T){ if(T!=NULL){ PostOrder(T->lchild); PostOrder(T->rchild); visit(T); } } // 应用:求树的深度 int treeDepth(BiTree T){ if(T == NULL){ return 0; }else{ int l = treeDepth(T->lchild); int r = treeDepth(T->rchild); return l>r ? l+1 r+1; } }
5.3.2. 二叉树的层序遍历
算法思想:
- 初始化一个辅助队列
- 根结点入队
- 若队列非空,则队头结点出队,访问该结点,并将其左、右孩子插入队尾(如果有的话)
- 重复第三步直至队列为空
代码实现:
// 二叉树结点
typedef struct BiTNode{
char data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
// 链式队列结点
typedef struct LinkNode{
BiTNode *data;
struct LinkNode *next;
}LinkNode;
typedef struct{
LinkNode *front, *rear;
}LinkQueue;
// 层序遍历
void LevelOrder(BiTree T){
LinkQueue Q;
InitQueue(Q);
BiTree p;
EnQueue(Q, T);
while(!IsEmpty(Q)){
DeQueue(Q, p);
visit(p);
if(p->lchild!=NULL)
EnQueue(Q, p->lchild);
if(p->rchild!=NULL)
EnQueue(Q, p->rchild);
}
}
5.3.3. 由遍历序列构造二叉树
-
一个前序遍历序列可能对应多种二叉树形态。同理,一个后序遍历序列、一个中序遍历序列、一个层序遍历序列也可能对应多种二叉树形态。即:若只给出一棵二叉树的 前/中/后/层序遍历序列 中的一种,不能唯一确定一棵二叉树。
-
由二叉树的遍历序列构造二叉树:
- 前序+中序遍历序列
- 后序+中序遍历序列
- 层序+中序遍历序列
-
由 前序+中序遍历序列 构造二叉树:由前序遍历的遍历顺序(根节点、左子树、右子树)可推出根节点,由根节点在中序遍历序列中的位置即可推出左子树与右子树分别有哪些结点。
-
由 后序+中序遍历序列 构造二叉树:由后序遍历的遍历顺序(左子树、右子树、根节点)可推出根节点,由根节点在中序遍历序列中的位置即可推出左子树与右子树分别有哪些结点。
-
由 层序+中序遍历序列 构造二叉树:由层序遍历的遍历顺序(层级遍历)可推出根节点,由根节点在中序遍历序列中的位置即可推出左子树与右子树分别有哪些结点。
5.3.4. 线索二叉树的概念
-
使用链式存储二叉树如何找到指定结点 p 在中序遍历序列中的前驱和后继?
答:从根节点出发,重新进行一次中序遍历,指针 q 记录当前访问的结点,指针 pre 记录上一个被访问的结点。当 q = = p q==p q==p 时,pre 为 q 的前驱结点;当 p r e = = p pre==p pre==p 时,q 为 p 的后继结点。
缺点:找前驱、后继很不方便;遍历操作必须从根结点开始。
-
n 个结点的二叉树,有 n+1 个空链域,可用来记录前驱、后继的信息。指向前驱、后继的指针被称为“线索”,形成的二叉树被称为线索二叉树。

-
线索二叉树的结点在原本二叉树的基础上,新增了左右线索标志 tag。当 tag == 0 时,表示指针指向孩子;当 tag == 1 时,表示指针是“线索”。
// 线索二叉树的结点 typedef struct ThreadNode{ ElemType data; struct ThreadNode *lchild, *rchild; int ltag, rtag; //左、右线索标志 } -
中序线索二叉树的存储:

- 先序线索二叉树的存储:

- 后序线索二叉树的存储:

5.3.5. 二叉树的线索化
中序线索化:
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag;
}ThreadNode, *ThreadTree;
// 中序遍历线索化二叉树
void InThread(ThreadTree &p, ThreadTree &pre) {
if (p != NULL) {
InThread(p->lchild, pre);
if (p->lchild == NULL) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
InThread(p->rchild, pre);
}
}
// 创建线索二叉树T
void CreateInThread(ThreadTree T) {
ThreadNode *pre = NULL;
if (T != NULL) {
InThread(T, pre);
pre->rchild = NULL;
pre->rtag = 1;
}
}
先序线索化:
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag;
}ThreadNode, *ThreadTree;
// 先序遍历线索化二叉树
void PreThread(ThreadTree &p, ThreadTree &pre){
if (p != NULL) {
if (p->lchild == NULL) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
PreThread(p->lchild, pre);
PreThread(p->rchild, pre);
}
}
// 创建线索二叉树
void CreatePreThread(ThreadTree T){
ThreadNode *pre = NULL;
if (T != NULL) {
PreThread(T, pre);
pre->rchild = NULL;
pre->rtag = 1;
}
}
后序线索化:
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag;
}ThreadNode, *ThreadTree;
// 后序遍历线索二叉树
void PostThread(ThreadTree &p, ThreadTree &pre){
PostThread(p->lchild, pre);
PostThread(p->rchild, pre);
if (p != NULL) {
if (p->lchild == NULL) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
}
}
// 后序线索化二叉树T
void CreatePostThread(ThreadTree T){
ThreadNode *pre = NULL;
if (T != NULL) {
PostThread(T, pre);
pre->rchild = NULL;
pre->rtag = 1;
}
}
5.3.6. 在线索二叉树中找前驱/后继
中序线索二叉树找到指定结点 * p 的中序后继 next:
- 若
p->rtag==1,则next = p->rchild; - 若
p->rtag==0,则 next 为 p 的右子树中最左下结点。
// 找到以p为根的子树中,第一个被中序遍历的结点
ThreadNode *FirstNode(ThreadNode *p){
// 循环找到最左下结点(不一定是叶结点)
while(p->ltag==0)
p=p->lchild;
return p;
}
// 在中序线索二叉树中找到结点p的后继结点
ThreadNode *NextNode(ThreadNode *p){
// 右子树中最左下的结点
if(p->rtag==0)
return FirstNode(p->rchild);
else
return p->rchild;
}
// 对中序线索二叉树进行中序循环(非递归方法实现)
void InOrder(ThreadNode *T){
for(ThreadNode *p=FirstNode(T); p!=NULL; p=NextNode(p)){
visit(p);
}
}
中序线索二叉树找到指定结点 * p 的中序前驱 pre:
- 若
p->ltag==1,则pre = p->lchild; - 若
p->ltag==0,则 next 为 p 的左子树中最右下结点。
// 找到以p为根的子树中,最后一个被中序遍历的结点
ThreadNode *LastNode(ThreadNode *p){
// 循环找到最右下结点(不一定是叶结点)
while(p->rtag==0)
p=p->rchild;
return p;
}
// 在中序线索二叉树中找到结点p的前驱结点
ThreadNode *PreNode(ThreadNode *p){
// 左子树中最右下的结点
if(p->ltag==0)
return LastNode(p->lchild);
else
return p->lchild;
}
// 对中序线索二叉树进行中序循环(非递归方法实现)
void RevOrder(ThreadNode *T){
for(ThreadNode *p=LastNode(T); p!=NULL; p=PreNode(p))
visit(p);
}
先序线索二叉树找到指定结点 * p 的先序后继 next:
- 若
p->rtag==1,则next = p->rchild; - 若
p->rtag==0:- 若 p 有左孩子,则先序后继为左孩子;
- 若 p 没有左孩子,则先序后继为右孩子。
先序线索二叉树找到指定结点 * p 的先序前驱 pre:
- 前提:改用三叉链表,可以找到结点 * p 的父节点。
- 如果能找到 p 的父节点,且 p 是左孩子:p 的父节点即为其前驱;
- 如果能找到 p 的父节点,且 p 是右孩子,其左兄弟为空:p 的父节点即为其前驱;
- 如果能找到 p 的父节点,且 p 是右孩子,其左兄弟非空:p 的前驱为左兄弟子树中最后一个被先序遍历的结点;
- 如果 p 是根节点,则 p 没有先序前驱。
后序线索二叉树找到指定结点 * p 的后序前驱 pre:
- 若
p->ltag==1,则pre = p->lchild; - 若
p->ltag==0:- 若 p 有右孩子,则后序前驱为右孩子;
- 若 p 没有右孩子,则后续前驱为右孩子。
后序线索二叉树找到指定结点 * p 的后序后继 next:
- 前提:改用三叉链表,可以找到结点 * p 的父节点。
- 如果能找到 p 的父节点,且 p 是右孩子:p 的父节点即为其后继;
- 如果能找到 p 的父节点,且 p 是左孩子,其右兄弟为空:p 的父节点即为其后继;
- 如果能找到 p 的父节点,且 p 是左孩子,其右兄弟非空:p 的后继为右兄弟子树中第一个被后序遍历的结点;
- 如果 p 是根节点,则 p 没有后序后继。
5.4. 树和森林
5.4.1. 树的存储结构
**双亲表示法(顺序存储):**每个结点中保存指向双亲的“指针”。
#define MAX_TREE_SIZE 100
// 树的结点
typedef struct{
ElemType data;
int parent;
}PTNode;
// 树的类型
typedef struct{
PTNode nodes[MAX_TREE_SIZE];
int n; //结点数量
}PTree;


孩子表示法(顺序+链式存储):
#define MAX_TREE_SIZE 100
struct CTNode{
int child; //孩子结点在数组中的位置
struct CTNode *next; //下一个孩子
}
typedef struct{
ElemType data;
struct CTNode *firstChild; //第一个孩子
}CTBox;
typedef struct{
CTBox node[MAX_TREE_SIZE];
int n,r; //结点数和根的位置
}CTree;

**孩子兄弟表示法(链式存储):**用孩子兄弟表示法可以将树转换为二叉树的形式。
//孩子兄弟表示法结点
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild, *nextsibling; //第一个孩子和右兄弟结点
}CSNode, *CSTree;

**森林和二叉树的转换:**森林是m(m≥0)棵互不相交的树的集合,可以将森林中的树看做一棵树中的兄弟结点,再使用孩子兄弟表示法将其转换为二叉树。
5.4.2. 树和森林的遍历
**树的先根遍历:**若树非空,先访问根结点, 再依次对每棵子树进行先根遍历。(深度优先遍历)
void PreOrder(TreeNode *R){
if(R!=NULL){
visit(R);
while(R还有下一个子树T)
PreOrder(T);
}
}
树的先根遍历序列与这棵树相应二叉树的先序序列相同。
**树的后根遍历:**若树非空,先依次对每棵子树进行后根遍历,最后再访问根结点。(深度优先遍历)
void PostOrder(TreeNode *R){
if(R!=NULL){
while(R还有下一个子树T)
PreOrder(T);
visit(R);
}
}
树的后根遍历序列与这棵树相应二叉树的中序序列相同。
树的层次遍历(用队列实现):
- 若树非空,则根节点入队;
- 若队列非空,队头元素出队并访问,同 时将该元素的孩子依次入队;
- 重复第二步直到队列为空
**森林的先序遍历:**若森林为非空,则按如下规则进行遍历:
- 访问森林中第一棵树的根结点。
- 先序遍历第一棵树中根结点的子树森林。
- 先序遍历除去第一棵树之后剩余的树构成的森林
森林的先序遍历效果等同于依次对各个树进行先根遍历,等同于对二叉树的先序遍历。
**森林的中序遍历:**若森林为非空,则按如下规则进行遍历:
- 中序遍历森林中第一棵树的根结点的子树森林。
- 访问第一棵树的根结点。
- 中序遍历除去第一棵树之后剩余的树构成的森林。
森林的中序遍历效果等同于依次对各个树进行后根遍历,等同于对二叉树的中序遍历。
5.5. 应用
5.5.1. 二叉排序树
-
二叉排序树,又称二叉查找树(BST,Binary Search Tree)。一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
- 左子树上所有结点的关键字均小于根结点的关键字;
- 右子树上所有结点的关键字均大于根结点的关键字;
- 左子树和右子树又各是一棵二叉排序树。
即:左子树结点值 < 根结点值 < 右子树结点值。因此,对二叉排序树进行中序遍历,可以得到一个递增的有序序列。
-
二叉排序树的查找:
// 二叉排序树结点
typedef struct BSTNode{
int key;
struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;
// 在二叉排序树中查找值为key的结点(非递归)
BSTNode *BST_Search(BSTree T, int key){
while(T!=NULL && key!=T->key){
if(key < T->key) T=T->lchild;
else T=T->rchild;
}
return T;
}
// 在二叉排序树中查找值为key的结点(递归实现)
BSTNode *BST_Search(BSTree T, int key){
if(T==NULL || T->key==key)
return T;
else if(key < T->key)
return BSTSearch(T->lchild, key);
else if(key > T->key)
return BSTSearch(T->rchild, key);
}
- **二叉排序树的插入:**若原二叉排序树为空,则直接插入结点;否则,若关键字 k 小于根结点值,则插入到左子树;若关键字 k 大于根结点值,则插入到右子树。
// 在二叉排序树中插入关键字为k的新节点(递归实现)
int BST_Insert(BSTree &T, int k){
if(T==NULL){
T=(BSTree)malloc(sizeof(BSTNode));
T->key=k;
T->lchild = T->rchild = NULL;
return 1;
}else if(k==T->key){
return 0;
}else if(k<T->key){
return BST_Insert(T->lchild, k);
}else
return BST_Insert(T->rchild, k);
}
- 二叉排序树的构造:
// 按照str[]中的关键字序列建立二叉排序树
void Creat_BST(BSTree &T, int str[], int n){
T=NULL;
int i=0;
while(i<n){
BST_Insert(T,str[i]);
i++;
}
}
-
**二叉排序树的删除:**先搜索找到目标结点:
- 若被删除结点 z 是叶结点,则直接删除,不会破坏二叉排序树的性质;
- 若结点 z 只有一棵左子树或右子树,则让 z 的子树成为 z 父结点的子树,替代 z 的位置;
- 若结点 z 有左、右两棵子树,则令 z 的直接后继(或直接前驱)替代 z ,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况。
-
**查找效率分析:**查找失败的平均查找长度 ASL(Average Search Length)

- A S L = ( 3 ∗ 7 + 4 ∗ 2 ) / 9 = 3.22 ASL=(3*7+4*2)/9=3.22 ASL=(3∗7+4∗2)/9=3.22
5.5.2. 平衡二叉树
-
平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树),树上任一结点的左子树和右子树的高度之差不超过 1。
结点的平衡因子 = 左子树高 - 右子树高
-
平衡二叉树的结点:
typedef struct AVLNode{
int key;
int balance; //平衡因子
struct AVLNode *lchild, *rchild;
}AVLNode, *AVLTree;
-
**调整最小不平衡子树:**在平衡二叉树的插入操作中,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡。调整可分为以下四种情况:
- LL:在A的左孩子的左子树中插入导致不平衡;
- RR:在A的右孩子的右子树中插入导致不平衡;
- LR:在A的左孩子的右子树中插入导致不平衡;
- RL:在A的右孩子的左子树中插入导致不平衡。
-
**调整最小不平衡子树(LL):**由于在结点 A 的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由 1增至 2,导致以 A 为根的子树失去平衡,需要一次向右的旋转操作。将 A 的左孩子 B 向右上旋转代替 A 成为根结点,将 A 结点向右下旋转成为 B 的右子树的根结点,而 B 的原右子树则作为 A 结点的左子树。

- **调整最小不平衡子树(RR):**由于在结点 A 的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由 -1 减至 -2,导致以 A 为根的子树失去平衡,需要一次向左的旋转操作。将 A 的右孩子 B 向左上旋转代替 A成为根结点,将 A 结点向左下旋转成为 B 的左子树的根结点,而 B 的原左子树则作为 A 结点的右子树。

- **调整最小不平衡子树(LR):**由于在 A 的左孩子(L)的右子树(R)上插入新结点,A 的平衡因子由 1 增至 2,导致以 A 为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。先将 A 结点的左孩子 B 的右子树的根结点 C 向左上旋转提升到 B 结点的位置,然后再把该 C 结点向右上旋转提升到 A 结点的位置。


- **调整最小不平衡子树(RL):**由于在 A 的右孩子(R)的左子树(L)上插入新结点,A 的平衡因子由 -1 减至 -2,导致以 A 为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A 结点的右孩子 B的左子树的根结点 C 向右上旋转提升到 B 结点的位置,然后再把该 C 结点向左上旋转提升到 A 结点的位置。


-
**查找效率分析:**若树高为h,则最坏情况下,查找一个关键字最多需要对比 h 次,即查找操作的时间复杂度不可能超过 O(h)。
由于平衡二叉树上任一结点的左子树和右子树的高度之差不超过 1,假如以 n h n_h nh表示深度为 h 的平衡树中含有的最少结点数,则有 n 0 = 0 n_0 = 0 n0=0, n 1 = 1 n_1 = 1 n1=1, n 2 = 2 n_2 = 2 n2=2,并且有 n h = n h − 1 + n h − 2 + 1 n_h = n_{h−1} + n_{h−2} +1 nh=nh−1+nh−2+1 。
5.5.3. 哈夫曼树
- 结点的权:有某种现实含义的数值。
- 结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积。
- 树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL,Weighted Path Length)。
W P L = ∑ i = 1 n w i l i WPL=\sum_{i=1}^{n}w_il_i WPL=i=1∑nwili
-
哈夫曼树的定义:在含有 n 个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树。
-
给定 n 个权值分别为 w 1 w_1 w1, w 2 w2 w2,…, w n w_n wn 的结点,构造哈夫曼树的算法描述如下:
- 将这 n 个结点分别作为 n 棵仅含一个结点的二叉树,构成森林 F。
- 构造一个新结点,从 F 中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和。
- 从 F 中删除刚才选出的两棵树,同时将新得到的树加入 F 中。
- 重复步骤 2 和 3,直至 F 中只剩下一棵树为止。
-
构造哈夫曼树的注意事项:
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大。
- 哈夫曼树的结点总数为 2n−1。
- 哈夫曼树中不存在度为 1 的结点。
- 哈夫曼树并不唯一,但 WPL 必然相同且为最优。

- 哈夫曼编码:字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树。
六、图
6.1. 图的基本概念
-
图:图 G 由顶点集 V 和边集 E 组成,记为 G = ( V , E ) G = (V, E) G=(V,E),其中 V ( G ) V(G) V(G) 表示图 G 中顶点的有限非空集; E ( G ) E(G) E(G) 表示图 G 中顶点之间的关系(边)集合。若 V = { v 1 , v 2 , … , v n } V = \{v1, v2, … , vn\} V={v1,v2,…,vn},则用 ∣ V ∣ |V| ∣V∣ 表示图 G 中顶点的个数,也称图 G 的阶; E = { ( u , v ) ∣ u ∈ V , v ∈ V } E = \{(u, v) | u\in V, v\in V\} E={(u,v)∣u∈V,v∈V},用 ∣ E ∣ |E| ∣E∣ 表示图 G 中边的条数。
注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集。
-
无向图:若 E 是无向边(也称边)的有限集合时,则图 G 为无向图。边是顶点的无序对,记为 ( v , w ) (v, w) (v,w) 或$ (w, v)$,其中 v、w 是顶点。可以说顶点 w 和顶点 v 互为邻接点,边 ( v , w ) (v, w) (v,w) 依附于顶点 w 和 v;或者说边 ( v , w ) (v, w) (v,w) 和顶点 v、w 相关联。
-
有向图:若 E 是有向边(也称弧)的有限集合时,则图 G 为有向图。 弧是顶点的有序对,记为 < v , w > <v,w> <v,w>,其中 v、w 是顶点,v 称为弧尾,w 称为弧头,称为从顶点 v 到顶点 w 的弧,也称 v邻接到w,或w邻接自v。 < v , w > ≠ < w , v > <v,w>\ne <w,v> <v,w>=<w,v>。
-
简单图:① 不存在重复边; ② 不存在顶点到自身的边。
-
多重图:图 G 某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联, 则 G 为多重图。

- 度、入度、出度:对于无向图,顶点 v 的度是指依附于该顶点的边的条数,记为 T D ( v ) TD(v) TD(v)。对于有向图,入度是以顶点 v 为终点的有向边的数目,记为 I D ( v ) ID(v) ID(v); 出度是以顶点 v 为起点的有向边的数目,记为 O D ( v ) OD(v) OD(v)。 顶点 v 的度等于其入度和出度之和,即 T D ( v ) = I D ( v ) + O D ( v ) TD(v) = ID(v) + OD(v) TD(v)=ID(v)+OD(v)。
- 路径:顶点 v p v_p vp 到顶点 v q v_q vq 之间的一条路径是指顶点序列 v p v_p vp, v i 1 v_{i1} vi1 , v i 2 v_{i2} vi2,…, v q v_q vq。
- 回路:第一个顶点和最后一个顶点相同的路径称为回路或环。
- 简单路径:在路径序列中,顶点不重复出现的路径称为简单路径。
- 简单回路:除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
- 路径长度:路径上边的数目。
- 点到点的距离:从顶点 u 出发到顶点 v 的最短路径若存在,则此路径的长度称为从 u 到 v 的距离。若从 u 到 v 根本不存在路径,则记该距离为无穷(∞)。
- 连通、强连通:无向图中,若从顶点 v 到顶点 w 有路径存在,则称 v 和 w 是连通的。有向图中,若从顶点 v 到顶点 w 和从顶点 w 到顶点 v 之间都有路径,则称这两个顶点是强连通的。
- 连通图:若图 G 中任意两个顶点都是连通的,则称图 G 为连通图,否则称为非连通图。对于 n 个顶点的无向图 G, 若 G 是连通图,则最少有 n-1 条边;若G是非连通图,则最多可能有 C n − 1 2 \mathrm{C}_{n-1}^2 Cn−12 条边。
- 子图、生成子图:设有两个图 G = ( V , E ) G = (V, E) G=(V,E) 和 G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′),若 V ′ V' V′ 是 V V V 的子集,且 E ′ E' E′ 是 E E E 的子集,则称 G ′ G' G′ 是 G G G 的子图。若有满足 V ( G ′ ) = V ( G ) V(G') = V(G) V(G′)=V(G) 的子图 G’,则称其为 G 的生成子图。

- 连通分量:无向图中的极大连通子图称为连通分量。

- 强连通分量:有向图中的极大强连通子图称为有向图的强连通分量。

- 生成树:连通图的生成树是包含图中全部顶点的一个极小连通子图。

- 生成森林:在非连通图中,连通分量的生成树构成了非连通图的生成森林。

-
边的权:在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。
-
带权图:边上带有权值的图称为带权图,也称网。
-
带权路径长度:当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度。
-
无向完全图:无向图中任意两个顶点之间都存在边。若无向图的顶点数 ∣ V ∣ = n |V|=n ∣V∣=n,则 ∣ E ∣ ∈ [ 0 , C n 2 ] |E|∈[0, \mathrm{C}_n^2] ∣E∣∈[0,Cn2] = [ 0 , n ( n – 1 ) / 2 ] [0, n(n–1)/2] [0,n(n–1)/2]。
-
有向完全图:有向图中任意两个顶点之间都存在方向相反的两条弧。若有向图的顶点数 ∣ V ∣ = n |V|=n ∣V∣=n,则 ∣ E ∣ ∈ [ 0 , 2 C n 2 ] = [ 0 , n ( n – 1 ) ] |E|∈[0, 2\mathrm{C}_n^2]=[0, n(n–1)] ∣E∣∈[0,2Cn2]=[0,n(n–1)]。
-
稀疏图、稠密图:边数很少的图称为稀疏图,反之称为稠密图。
6.2. 图的存储
6.2.1. 邻接矩阵
邻接矩阵存储无向图、有向图:
#define MaxVertexNum 100 //顶点数目的最大值
typedef struct{
char Vex[MaxVertexNum]; //顶点表
int Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum,arcnum; //图的顶点数和边数
}MGraph;

度:第 i 个结点的度 = 第 i 行(或第 i 列)的非零元素个数;
出度:第 i 行的非零元素个数;
入度:第 i 列的非零元素个数。
邻接矩阵法存储带权图:
#define MaxVertexNum 100 //顶点数目的最大值
#define INFINITY 2147483647; //表示“无穷”
typedef char VertexType; //顶点数据类型
typedef int EdgeType; //边数据类型
typedef struct{
VertexType Vex[MaxVertexNum]; //顶点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //边的权值
int vexnum,arcnum; //图的当前顶点数和弧数
}MGraph;

性能分析:
- 空间复杂度: O ( ∣ V ∣ 2 ) O(|V|^2 ) O(∣V∣2) ,只和顶点数相关,和实际的边数无关。
- 适合用于存储稠密图。
- 无向图的邻接矩阵是对称矩阵,可以压缩存储(只存储上三角区或者下三角区)。
**邻接矩阵的性质:**设图 G 的邻接矩阵为 A(矩阵元素为 0 或 1),则 A n A^n An 的元素 A n [ i ] [ j ] A^n[i][j] An[i][j] 等于由顶点 i 到顶点 j 的长度为 n 的路径的数目。
6.2.2. 邻接表
邻接表存储存储无向图、有向图:
#define MVNum 100 //最大顶点数
typedef struct ArcNode{ //边/弧
int adjvex; //邻接点的位置
struct ArcNode *next; //指向下一个表结点的指针
}ArcNode;
typedef struct VNode{
char data; //顶点信息
ArcNode *first; //第一条边/弧
}VNode, AdjList[MVNum]; //AdjList表示邻接表类型
typedef struct{
AdjList vertices; //头结点数组
int vexnum, arcnum; //当前的顶点数和边数
}ALGraph;

对比邻接矩阵:
| 邻接表 | 邻接矩阵 | |
|---|---|---|
| 空间复杂度 | 无向图:$O( | V |
| 适用场景 | 存储稀疏图 | 存储稠密图 |
| 表示方式 | 不唯一 | 唯一 |
| 计算度、入度、出度 | 计算有向图的度、入度不方便,其余很方便 | 遍历对应行或列 |
| 找相邻的边 | 找有向图的入边不方便,其余很方便 | 遍历对应行或列 |
6.2.3. 十字链表、临接多重表
十字链表存储有向图:
#define MAX_VERTEX_NUM 20 //最大顶点数量
typedef struct ArcBox{ //弧结点
int tailvex, headvex; //弧尾,弧头顶点编号(一维数组下标)
struct ArcBox *hlink, *tlink; //弧头相同、弧尾相同的下一条弧的链域
InfoType info; //权值
}ArcBox;
typedef struct VexNode{ //顶点结点
VertexType data; //顶点数据域
ArcBox *firstin, *firstout; //该顶点的第一条入弧和第一条出弧
}VexNode;
typedef struct{ //有向图
VexNode xlist[MAX_VERTEX_NUM]; //存储顶点的一维数组
int vexnum, arcnum; //有向图的当前顶点数和弧数
}OLGraph;

邻接多重表存储无向图:
#define MAX_VERTEX_NUM 20 //最大顶点数量
struct EBox{ //边结点
int i,j; //该边依附的两个顶点的位置(一维数组下标)
EBox *ilink,*jlink; //分别指向依附这两个顶点的下一条边
InfoType info; //边的权值
};
struct VexBox{
VertexType data;
EBox *firstedge; //指向第一条依附该顶点的边
};
struct AMLGraph{
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum,edgenum; //无向图的当前顶点数和边数
};

四种存储方法比较:
| 邻接矩阵 | 邻接表 | 十字链表 | 邻接多重表 | |
|---|---|---|---|---|
| 空间复杂度 | $O( | V | ^2)$ | 无向图:$O( |
| 找相邻边 | 遍历对应行或列 | 找有向图的入边必须遍历整个邻接表 | 很方便 | 很方便 |
| 删除顶点或边 | 删除边很方便,删除顶点需要大量移动数据 | 无向图中删除边或顶点都不方便 | 很方便 | 很方便 |
| 适用场景 | 存储稠密图 | 存储稀疏图 | 存储有向图 | 存储无向图 |
| 表示方式 | 唯一 | 不唯一 | 不唯一 | 不唯一 |
6.2.4. 图的基本操作
-
Adjacent(G, x, y):判断图 G 是否存在边 < x , y > <x,y> <x,y> 或 ( x , y ) (x, y) (x,y)。 -
Neighbors(G, x):列出图 G 中与结点 x 邻接的边。 -
InsertVertex(G, x):在图 G 中插入顶点 x 。 -
DeleteVertex(G, x):从图 G 中删除顶点 x。 -
AddEdge(G, x, y):若无向边 ( x , y ) (x, y) (x,y) 或有向边 < x , y > <x,y> <x,y> 不存在,则向图 G 中添加该边。 -
RemoveEdge(G, x, y):若无向边 ( x , y ) (x, y) (x,y) 或有向边 < x , y > <x,y> <x,y> 存在,则从图 G 中删除该边。 -
FirstNeighbor(G, x):求图 G 中顶点 x 的第一个邻接点,若有则返回顶点号。若 x 没有邻接点或图中不存在 x,则返回 -1。 -
NextNeighbor(G, x, y):假设图 G 中顶点 y 是顶点 x 的一个邻接点,返回除 y 之外顶点 x 的下一个邻接点的顶点号,若 y 是 x 的最后一个邻接点,则返回 -1。 -
Get_edge_value(G, x, y):获取图 G 中边 ( x , y ) (x, y) (x,y) 或 < x , y > <x,y> <x,y> 对应的权值。 -
Set_edge_value(G, x, y, v):设置图 G 中边 ( x , y ) (x, y) (x,y) 或 < x , y > <x,y> <x,y> 对应的权值为 v。
6.3. 图的遍历
6.3.1. 广度优先遍历
-
⼴度优先遍历(Breadth-First-Search, BFS)要点:
- 找到与⼀个顶点相邻的所有顶点;
- 标记哪些顶点被访问过;
- 需要⼀个辅助队列。
-
广度优先遍历用到的操作:
-
FirstNeighbor(G, x):求图 G 中顶点 x 的第⼀个邻接点,若有则返回顶点号;若 x 没有邻接点或图中不存在 x,则返回 -1。 -
NextNeighbor(G, x, y):假设图 G 中顶点 y 是顶点 x 的⼀个邻接点,返回除 y 之外顶点 x 的下⼀个邻接点的顶点号,若 y 是 x 的最后⼀个邻接点,则返回 -1。
-
-
广度优先遍历伪代码:
bool visited[MAX_VERTEX_NUM]; //访问标记数组
// 对图G进行广度优先遍历
void BFSTraverse(Graph G){
for(i=0; i<G.vexnum; ++i) //访问标记数组初始化
visited[i]=FALSE;
InitQueue(Q); //初始化辅助队列
for(i=0; i<G.vexnum; ++i) //从0号结点开始遍历,对每个连通分量进行一次广度优先遍历
if(!visited[i])
BFS(G,i);
}
//从顶点v开始广度优先遍历图G
void BFS(Graph G,int v){
visit(G,v); //访问图G的结点v
visited[v]=TREE; //标记v已被访问
EnQueue(Q,v); //顶点v入队列Q
while(!isEmpty(Q)){
DeQueue(Q,v); //队列头节点出队并将头结点的值赋给v
for(w=FirstNeighbor(G,v); w>=0; w=NextNeighbor(G,v,w)){
//检测v的所有邻结点
if(!visited[w]){
visit(w);
visited[w]=TREE;
EnQueue(Q,w);
}
}
}
}
-
复杂度分析:
- 空间复杂度:最坏情况,辅助队列⼤⼩为 O ( ∣ V ∣ ) O(|V|) O(∣V∣)。
- 对于邻接矩阵存储的图,访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,查找每个顶点的邻接点都需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,⽽总共有 ∣ V ∣ |V| ∣V∣ 个顶点,时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2)。
- 对于邻接表存储的图,访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,查找各个顶点的邻接点共需要 O ( ∣ E ∣ ) O(|E|) O(∣E∣) 的时间, 时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O(∣V∣+∣E∣)。
-
⼴度优先⽣成树:⼴度优先⽣成树由⼴度优先遍历过程确定。由于邻接表的表示⽅式不唯⼀,因此基于邻接表的⼴度优先⽣成树也不唯⼀。

6.3.2. 深度优先遍历
- 递归实现DFS算法:
bool visited[MAX_VERTEX_NUM]; //访问标记数组
// 对图G进行深度优先算法
void DFSTraverse(Graph G){
for(v=0; v<G.vexnum; v++){ //初始化标记数组
visited[v]=FALSE;
}
for(v=0; v<G.vexnum; v++){
if(!visited[v])
DFS(G,v);
}
}
// 从顶点v出发深度优先遍历图G
void DFS(Graph G,int v){
visit(G,v);
visited[v]=TREE;
for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v)){
if(!visited[w])
DFS(G,v);
}
}
-
复杂度分析:
- 空间复杂度主要来自来⾃函数调⽤栈,最坏情况下递归深度为 O ( ∣ V ∣ ) O(|V|) O(∣V∣);最好情况为 O ( 1 ) O(1) O(1)
- 对于邻接矩阵存储的图,访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,查找每个顶点的邻接点都需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,⽽总共有 ∣ V ∣ |V| ∣V∣ 个顶点,时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2)。
- 对于邻接表存储的图,访问 ∣ V ∣ |V| ∣V∣ 个顶点需要 O ( ∣ V ∣ ) O(|V|) O(∣V∣) 的时间,查找各个顶点的邻接点共需要 O ( ∣ E ∣ ) O(|E|) O(∣E∣) 的时间, 时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O(∣V∣+∣E∣)。
-
深度优先遍历序列:

- 从 2 出发的深度优先遍历序列:2, 1, 5, 6, 3, 4, 7, 8
- 从 3 出发的深度优先遍历序列:3, 4, 7, 6, 2, 1, 5, 8
- 从 1 出发的深度优先遍历序列:1, 2, 6, 3, 4, 7, 8, 5
- 深度优先⽣成树:


同⼀个图的邻接矩阵表示⽅式唯⼀,因此深度优先遍历序列唯⼀,深度优先⽣成树也唯⼀;
同⼀个图的邻接表表示⽅式不唯⼀,因此深度优先遍历序列不唯⼀,深度优先⽣成树也不唯⼀。
- 图的遍历与图的连通性:
- 对⽆向图进⾏ BFS/DFS 遍历,调⽤ BFS/DFS函数的次数=连通分量数。对于连通图,只需调⽤ 1 次 BFS/DFS函数。
- 对有向图进⾏ BFS/DFS 遍历,调⽤ BFS/DFS函数的次数要具体问题具体分析。若起始顶点到其他各顶点都有路径,则只需调⽤ 1 次 BFS/DFS函数。对于强连通图,从任⼀结点出发都只需调⽤ 1 次 BFS/DFS函数。
6.4. 图的应用
6.4.1. 最小生成树
- 生成树:连通图的生成树是包含图中全部顶点的一个极小连通子图。 若图中顶点数为 n,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。
- 最⼩⽣成树(最⼩代价树):对于⼀个带权连通⽆向图
G
=
(
V
,
E
)
G = (V, E)
G=(V,E),⽣成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设 R 为 G 的所有⽣成树的集合,若 T 为 R 中边的权值之和最⼩的⽣成树,则 T 称为 G 的最⼩⽣成树(Minimum-Spanning-Tree, MST)。
- 最⼩⽣成树可能有多个,但边的权值之和总是唯⼀且最⼩的。
- 最⼩⽣成树的边数 = 顶点数 - 1。砍掉⼀条则不连通,增加⼀条边则会出现回路。
- 如果⼀个连通图本身就是⼀棵树,则其最⼩⽣成树就是它本身。
- 只有连通图才有⽣成树,⾮连通图只有⽣成森林。
- Prim 算法(普⾥姆):从某⼀个顶点开始构建⽣成树,每次将代价最⼩的新顶点纳⼊⽣成树,直到所有顶点都纳⼊为⽌。
- Kruskal 算法(克鲁斯卡尔):每次选择⼀条权值最⼩的边,使这条边的两头连通(原本已经连通的就不选),直到所有结点都连通。
| Prim 算法(普⾥姆) | Kruskal 算法(克鲁斯卡尔) | |
|---|---|---|
| 时间复杂度 | $O( | V |
| 适用场景 | 稠密图 | 稀疏图 |
6.4.2. 无权图的单源最短路径问题——BFS算法
⽆权图可以视为每条边的权值都为 1 的带权图。
-
使用 BFS算法求无权图的最短路径问题,需要使用三个数组:
-
d[]数组用于记录顶点 u 到其他顶点的最短路径。 -
path[]数组用于记录最短路径从那个顶点过来。 -
visited[]数组用于记录是否被访问过。
-
-
代码实现:
#define MAX_LENGTH 2147483647 //地图中最大距离,表示正无穷
// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){
for(i=0; i<G.vexnum; i++){
visited[i]=FALSE; //初始化访问标记数组
d[i]=MAX_LENGTH; //初始化路径长度
path[i]=-1; //初始化最短路径记录
}
InitQueue(Q); //初始化辅助队列
d[u]=0;
visites[u]=TREE;
EnQueue(Q,u);
while(!isEmpty[Q]){ //BFS算法主过程
DeQueue(Q,u); //队头元素出队并赋给u
for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w)){
if(!visited[w]){
d[w]=d[u]+1;
path[w]=u;
visited[w]=TREE;
EnQueue(Q,w); //顶点w入队
}
}
}
}
6.4.3. 单源最短路径问题——Dijkstra算法
- BFS算法的局限性:BFS算法求单源最短路径只适⽤于⽆权图,或所有边的权值都相同的图。
- 使用 Dijkstra算法求最短路径问题,需要使用三个数组:
-
final[]数组用于标记各顶点是否已找到最短路径。 -
dist[]数组用于记录各顶点到源顶点的最短路径长度。 -
path[]数组用于记录各顶点现在最短路径上的前驱。
-

- 代码实现:
#define MAX_LENGTH = 2147483647;
// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){
for(int i=0; i<G.vexnum; i++){ //初始化数组
final[i]=FALSE;
dist[i]=G.edge[u][i];
if(G.edge[u][i]==MAX_LENGTH || G.edge[u][i] == 0)
path[i]=-1;
else
path[i]=u;
final[u]=TREE;
}
for(int i=0; i<G.vexnum; i++){
int MIN=MAX_LENGTH;
int v;
// 循环遍历所有结点,找到还没确定最短路径,且dist最⼩的顶点v
for(int j=0; j<G.vexnum; j++){
if(final[j]!=TREE && dist[j]<MIN){
MIN = dist[j];
v = j;
}
}
final[v]=TREE;
// 检查所有邻接⾃v的顶点路径长度是否最短
for(int j=0; j<G.vexnum; j++){
if(final[j]!=TREE && dist[j]>dist[v]+G.edge[v][j]){
dist[j] = dist[v]+G.edge[v][j];
path[j] = v;
}
}
}
}
Dijkstra算法能够很好的处理带权图的单源最短路径问题,但不适⽤于有负权值的带权图。
6.4.4. 各顶点间的最短路径问题——Floyd算法
-
Floyd算法:求出每⼀对顶点之间的最短路径,使⽤动态规划思想,将问题的求解分为多个阶段。
-
Floyd算法使用到两个矩阵:
-
dist[][]:目前各顶点间的最短路径。 -
path[][]:两个顶点之间的中转点。
-
-
代码实现:
int dist[MaxVertexNum][MaxVertexNum];
int path[MaxVertexNum][MaxVertexNum];
void Floyd(MGraph G){
int i,j,k;
// 初始化部分
for(i=0;i<G.vexnum;i++){
for(j=0;j<G.vexnum;j++){
dist[i][j]=G.Edge[i][j];
path[i][j]=-1;
}
}
// 算法核心部分
for(k=0;k<G.vexnum;k++){
for(i=0;i<G.vexnum;i++){
for(j=0;j<G.vexnum;j++){
if(dist[i][j]>dist[i][k]+dist[k][j]){
dist[i][j]=dist[i][k]+dist[k][j];
path[i][j]=k;
}
}
}
}
}
Floyd算法可以⽤于负权值带权图,但是不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径。
- 最短路径算法比较:
| BFS算法 | Dijkstra算法 | Floyd算法 | |
|---|---|---|---|
| 无权图 | ✔ | ✔ | ✔ |
| 带权图 | ✘ | ✔ | ✔ |
| 带负权值的图 | ✘ | ✘ | ✔ |
| 带负权回路的图 | ✘ | ✘ | ✘ |
| 时间复杂度 | $O( | V^2 | ) 或 或 或O( |
| 通常⽤于 | 求⽆权图的单源最短路径 | 求带权图的单源最短路径 | 求带权图中各顶点间的最短路径 |
6.4.5. 有向⽆环图描述表达式
- 有向⽆环图:若⼀个有向图中不存在环,则称为有向⽆环图,简称 DAG图(Directed Acyclic Graph)。
用有向无环图描述表达式 ( ( a + b ) ∗ ( b ∗ ( c + d ) ) + ( c + d ) ∗ e ) ∗ ( ( c + d ) ∗ e ) ((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e) ((a+b)∗(b∗(c+d))+(c+d)∗e)∗((c+d)∗e)

- 有向无环图描述表达式的解题步骤:
- 把各个操作数不重复地排成⼀排;
- 标出各个运算符的⽣效顺序(先后顺序有点出⼊⽆所谓);
- 按顺序加⼊运算符,注意“分层”;
- 从底向上逐层检查同层的运算符是否可以合并。
6.4.6. 拓扑排序
- AOV⽹(Activity On Vertex NetWork,⽤顶点表示活动的⽹):⽤ DAG 图(有向⽆环图)表示⼀个⼯程。顶点表示活动,有向边 < V i , V j > <V_i,V_j> <Vi,Vj> 表示活动 V i V_i Vi 必须先于活动 V j V_j Vj 进⾏。

-
拓扑排序:在图论中,由⼀个有向⽆环图的顶点组成的序列,当且仅当满⾜下列条件时,称为该图的⼀个拓扑排序:
- 每个顶点出现且只出现⼀次;
- 若顶点 A 在序列中排在顶点 B 的前⾯,则在图中不存在从顶点 B 到顶点 A 的路径。
或定义为:拓扑排序是对有向⽆环图的顶点的⼀种排序,它使得若存在⼀条从顶点 A 到顶点 B 的路径,则在排序中顶点 B 出现在顶点 A 的后⾯。每个 AOV ⽹都有⼀个或多个拓扑排序序列。
-
拓扑排序的实现:
- 从 AOV ⽹中选择⼀个没有前驱(⼊度为0)的顶点并输出。
- 从⽹中删除该顶点和所有以它为起点的有向边。
- 重复 ① 和 ② 直到当前的 AOV ⽹为空或当前⽹中不存在⽆前驱的顶点为⽌。
例如,“番茄炒蛋工程”的其中一个拓扑排序为:准备厨具,买菜,洗番茄,切番茄,打鸡蛋,下锅炒,吃。
- 代码实现拓扑排序(邻接表实现):
#define MaxVertexNum 100 //图中顶点数目最大值
typedef struct ArcNode{ //边表结点
int adjvex; //该弧所指向的顶点位置
struct ArcNode *nextarc; //指向下一条弧的指针
}ArcNode;
typedef struct VNode{ //顶点表结点
VertexType data; //顶点信息
ArcNode *firstarc; //指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];
typedef struct{
AdjList vertices; //邻接表
int vexnum,arcnum; //图的顶点数和弧数
}Graph; //Graph是以邻接表存储的图类型
// 对图G进行拓扑排序
bool TopologicalSort(Graph G){
InitStack(S); //初始化栈,存储入度为0的顶点
for(int i=0;i<g.vexnum;i++){
if(indegree[i]==0)
Push(S,i); //将所有入度为0的顶点进栈
}
int count=0; //计数,记录当前已经输出的顶点数
while(!IsEmpty(S)){ //栈不空,则存入
Pop(S,i); //栈顶元素出栈
print[count++]=i; //输出顶点i
for(p=G.vertices[i].firstarc;p;p=p=->nextarc){
//将所有i指向的顶点的入度减1,并将入度为0的顶点压入栈
v=p->adjvex;
if(!(--indegree[v]))
Push(S,v); //入度为0,则入栈
}
}
if(count<G.vexnum)
return false; //排序失败
else
return true; //排序成功
}
6.4.7. 关键路径
- AOE 网:在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如 完成活动所需的时间),称之为⽤边表示活动的⽹络,简称 AOE ⽹ (Activity On Edge NetWork)。

-
AOE⽹具有以下两个性质:
- 只有在某顶点所代表的事件发⽣后,从该顶点出发的各有向边所代表的活动才能开始;
- 只有在进⼊某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发⽣。 另外,有些活动是可以并⾏进⾏的。
-
在 AOE ⽹中仅有⼀个⼊度为 0 的顶点,称为开始顶点(源点),它表示整个⼯程的开始; 也仅有⼀个出度为 0 的顶点,称为结束顶点(汇点),它表示整个⼯程的结束。
-
从源点到汇点的有向路径可能有多条,所有路径中,具有最⼤路径⻓度的路径称为关键路径,⽽把关键路径上的活动称为关键活动。完成整个⼯程的最短时间就是关键路径的⻓度,若关键活动不能按时完成,则整个 ⼯程的完成时间就会延⻓。
-
术语:
- 事件 v k v_k vk 的最早发⽣时间 v e ( k ) ve(k) ve(k):决定了所有从 v k vk vk 开始的活动能够开⼯的最早时间。
- 事件 v k v_k vk 的最迟发⽣时间 v l ( k ) vl(k) vl(k):它是指在不推迟整个⼯程完成的前提下,该事件最迟必须发⽣的时间。
- 活动 a i a_i ai 的最早开始时间 e ( i ) e(i) e(i):指该活动弧的起点所表⽰的事件的最早发⽣时间。
- 活动 a i a_i ai 的最迟开始时间 l ( i ) l(i) l(i):它是指该活动弧的终点所表示事件的最迟发⽣时间与该活动所需时间之差。
- 活动 a i a_i ai 的时间余量 d ( i ) = l ( i ) − e ( i ) d(i)=l(i)-e(i) d(i)=l(i)−e(i),表⽰在不增加完成整个⼯程所需总时间的情况下,活动 a i a_i ai 可以拖延的时间若⼀个活动的时间余量为零,则说明该活动必须要如期完成, d ( i ) = 0 d(i)=0 d(i)=0 即 l ( i ) = e ( i ) l(i) = e(i) l(i)=e(i) 的活动 a i a_i ai 是关键活动,由关键活动组成的路径就是关键路径。
-
求关键路径的步骤:
- 求所有事件的最早发⽣时间 v e ( ) ve( ) ve():按拓扑排序序列,依次求各个顶点的 v e ( k ) ve(k) ve(k), v e ( 源 点 ) = 0 ve(源点) = 0 ve(源点)=0, v e ( k ) = M a x { v e ( j ) + W e i g h t ( v j , v k ) } ve(k) = Max\{ve(j) + Weight(v_j, v_k)\} ve(k)=Max{ve(j)+Weight(vj,vk)}, v j v_j vj 为 v k v_k vk 的任意前驱。
- 求所有事件的最迟发⽣时间 v l ( ) vl( ) vl():按逆拓扑排序序列,依次求各个顶点的 v l ( k ) vl(k) vl(k), v l ( 汇 点 ) = v e ( 汇 点 ) vl(汇点)=ve(汇点) vl(汇点)=ve(汇点) , v l ( k ) = M i n { v l ( j ) − W e i g h t ( v k , v j ) } vl(k) = Min\{ vl(j) - Weight(v_k, v_j)\} vl(k)=Min{vl(j)−Weight(vk,vj)}, v j v_j vj 为 v k v_k vk 的任意后继。
- 求所有活动的最早发⽣时间 e ( ) e( ) e():若边 < v k , v j > <v_k,v_j> <vk,vj> 表⽰活动 a i a_i ai,则有 e ( i ) = v e ( k ) e(i) = ve(k) e(i)=ve(k)。
- 求所有活动的最迟发⽣时间 l ( ) l( ) l():若边 < v k , v j > <v_k,v_j> <vk,vj> 表⽰活动 a i a_i ai,则有 l ( i ) = v l ( j ) − W e i g h t ( v k , v j ) l(i) = vl(j)-Weight(v_k,v_j) l(i)=vl(j)−Weight(vk,vj)。
- 求所有活动的时间余量 d ( ) d( ) d(): d ( i ) = l ( i ) − e ( i ) d(i) = l(i) - e(i) d(i)=l(i)−e(i)。
-
关键活动、关键路径的特性:
- 若关键活动耗时增加,则整个⼯程的⼯期将增⻓。
- 缩短关键活动的时间,可以缩短整个⼯程的⼯期。
- 当缩短到⼀定程度时,关键活动可能会变成⾮关键活动。
- 可能有多条关键路径,只提⾼⼀条关键路径上的关键活动速度并不能缩短整个⼯程的⼯期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短⼯期的⽬的。
七、查找
7.1. 基本概念
- 查找:在数据集合中寻找满⾜某种条件的数据元素的过程称为查找。
- 查找表(查找结构):⽤于查找的数据集合称为查找表,它由同⼀类型的数据元素(或记录)组成。
- 关键字:数据元素中唯⼀标识该元素的某个数据项的值,使⽤基于关键字的查找,查找结果应该是唯⼀的。
- 对查找表的常⻅操作:
- 查找符合条件的数据元素
- 插⼊、删除某个数据元素
只进⾏查找操作最好使用静态查找表,若需要进⾏大量插入删除操作可使用动态查找表。
- 查找⻓度:在查找运算中,需要对⽐关键字的次数称为查找⻓度。
- 平均查找⻓度(ASL, Average Search Length):所有查找过程中进⾏关键字的⽐较次数的平均值。
A S L = ∑ i = 1 n P i C i ASL=\sum ^n_{i=1}P_iC_i ASL=i=1∑nPiCi
7.2. 顺序查找和折半查找
7.2.1. 顺序查找
- 顺序查找:⼜叫“线性查找”,通常⽤于线性表。
- 算法思想:从头到尾挨个找(或者从尾到头)。
- 代码实现:
typedef struct{ //查找表的数据结构(顺序表)
ElemType *elem; //动态数组基址
int TableLen; //表的长度
}SSTable;
//顺序查找
int Search_Seq(SSTable ST,ElemType key){
int i;
for(i=0;i<ST.TableLen && ST.elem[i]!=key;++i);
// 查找成功返回数组下标,否则返回-1
return i=ST.TableLen? -1 : i;
}
- 哨兵方式:
typedef struct{ //查找表的数据结构(顺序表)
ElemType *elem; //动态数组基址
int TableLen; //表的长度
}SSTable;
//顺序查找
int Search_Seq(SSTable ST,ElemType key){
ST.elem[0]=key;
int i;
for(i=ST.TableLen;ST.elem[i]!=key;--i)
// 查找成功返回数组下标,否则返回0
return i;
}
7.2.2. 折半查找
- 折半查找:⼜称“⼆分查找”,仅适⽤于有序的顺序表。(顺序表拥有随机访问 的特性,链表没有)
- 代码实现:
typedef struct{
ElemType *elem;
int TableLen;
}SSTable;
// 折半查找
int Binary_Search(SSTable L,ElemType key){
int low=0,high=L.TableLen,mid;
while(low<=high){
mid=(low+high)/2;
if(L.elem[mid]==key)
return mid;
else if(L.elem[mid]>key)
high=mid-1; //从前半部分继续查找
else
low=mid+1; //从后半部分继续查找
}
return -1;
}
- 折半查找判定树的构造: m i d = ⌊ ( l o w + h i g h ) / 2 ⌋ mid=\lfloor (low+high)/2\rfloor mid=⌊(low+high)/2⌋,如果当前 low 和 high 之间有奇数个元素,则 mid 分隔后,左右两部分元素个数相等;如果当前 low 和 high 之间有偶数个元素,则 mid 分隔后,左半部分⽐右半部分少⼀个元素。
- 折半查找的判定树中,若 m i d = ⌊ ( l o w + h i g h ) / 2 ⌋ mid=\lfloor (low+high)/2\rfloor mid=⌊(low+high)/2⌋ ,则对于任何⼀个结点,必有:右⼦树结点数 - 左⼦树结点数 = 0 或 1。
- 折半查找的判定树⼀定是平衡⼆叉树。折半查找的判定树中,只有最下⾯⼀层是不满的。因此,元素个数为 n 时树⾼ h = ⌈ l o g 2 ( n + 1 ) ⌉ h = ⌈log_2(n + 1)⌉ h=⌈log2(n+1)⌉。
- 判定树结点关键字:左<中<右,满⾜⼆叉排序树的定义。失败结点:n+1个(等于成功结点的空链域数量)
- 折半查找的查找效率:折半查找的时间复杂度 = O ( l o g 2 n ) O(log_2n) O(log2n)。
7.2.3. 分块查找
- 分块查找所针对的情况:块内⽆序、块间有序。

- 索引表及顺序表代码:
// 索引表
typedef struct{
ElemType maxValue;
int low,high;
}Index;
// 顺序表存储实际元素
ElemType List[100];
- 查找目标关键字所在分块可使用顺序查找和折半查找两种方式。
- 若使用折半查找且索引表中不包含⽬标关键字,则最终要停在 low > high,要在 low 所指分块中查找目标关键字。
- 查找效率分析(ASL):假设⻓度为 n 的查找表被均匀地分为 b 块,每块 s 个元素。设索引查找和块内查找的平均查找⻓度分别为 L I L_I LI、 L S L_S LS,则分块查找的平均查找⻓度为: A S L = L I + L S ASL=L_I + L_S ASL=LI+LS

-
⽤顺序查找查索引表,则 L I = 1 + 2 + . . . + b b = b + 1 2 L_I=\frac{1+2+...+b}{b}=\frac{b+1}{2} LI=b1+2+...+b=2b+1, L S = 1 + 2 + . . . + S S = S + 1 2 L_S=\frac{1+2+...+S}{S}=\frac{S+1}{2} LS=S1+2+...+S=2S+1, A S L = s 2 + 2 s + n 2 s ASL=\frac{s^2+2s+n}{2s} ASL=2ss2+2s+n。故当 s = n s=\sqrt n s=n时,ASL 最小,为 n + 1 \sqrt{n}+1 n+1。
-
⽤顺序查找查索引表,则 L I = ⌈ l o g 2 ( b + 1 ) ⌉ L_I=\lceil log_2(b+1)\rceil LI=⌈log2(b+1)⌉, L S = 1 + 2 + . . . + S S = S + 1 2 L_S=\frac{1+2+...+S}{S}=\frac{S+1}{2} LS=S1+2+...+S=2S+1,则 A S L = S + 1 2 + ⌈ l o g 2 ( b + 1 ) ⌉ ASL=\frac{S+1}{2}+\lceil log_2(b+1)\rceil ASL=2S+1+⌈log2(b+1)⌉
7.3. B树、B+树
7.3.1. B树
-
B树,⼜称多路平衡查找树,B树中所有结点的孩⼦个数的最⼤值称为B树的阶,通常⽤m表示。⼀棵m阶B树或为空树,或为满⾜如下特性的m叉树:
-
树中每个结点⾄多有 m 棵⼦树,即⾄多含有 m-1 个关键字。
-
若根结点不是终端结点,则⾄少有两棵⼦树。
-
除根结点外的所有⾮叶结点⾄少有 ⌈ m / 2 ⌉ \lceil m/2\rceil ⌈m/2⌉ 棵⼦树,即⾄少含有 $\lceil m/2\rceil-1 $个关键字。(为了保证查找效率,每个结点的关键字不能太少)
-
所有⾮叶结点的结构如下:

其中, K i ( i = 1 , 2 , … , n ) K_i(i = 1, 2,…, n) Ki(i=1,2,…,n) 为结点的关键字,且满⾜ K 1 < K 2 < … < K n K_1 < K_2 <…< K_n K1<K2<…<Kn; P i ( i = 0 , 1 , … , n ) P_i(i = 0,1,…, n) Pi(i=0,1,…,n) 为指向⼦树根结点的指针,且指针 P i − 1 P_{i-1} Pi−1 所指⼦树中所有结点的关键字均⼩于 K i K_i Ki, P i P_i Pi 所指⼦树中所有结点的关键字均⼤于 K i Ki Ki, n ( ⌈ m / 2 ⌉ − 1 ≤ n ≤ m − 1 ) n(⌈m/2⌉- 1≤n≤m - 1) n(⌈m/2⌉−1≤n≤m−1) 为结点中关键字的个数。
-
所有的叶结点都出现在同⼀层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)。
-

-
m阶B树的核⼼特性:
-
根节点的⼦树数 ∈ [ 2 , m ] ∈[2, m] ∈[2,m],关键字数 ∈ [ 1 , m − 1 ] ∈[1, m-1] ∈[1,m−1]。
其他结点的⼦树数 ∈ [ ⌈ m / 2 ⌉ , m ] ∈[⌈m/2⌉ , m] ∈[⌈m/2⌉,m];关键字数 ∈ [ − 1 , m − 1 ] ∈[ -1, m-1] ∈[−1,m−1]。
-
对任⼀结点,其所有⼦树⾼度都相同。
-
关键字的值:⼦树0 < 关键字1 < ⼦树1 < 关键字2 < ⼦树2 <…. (类⽐⼆叉查找树左<中<右)
-
-
B树的⾼度:含 n 个关键字的 m叉B树,最⼩⾼度、最⼤⾼度是多少?
l o g m n + 1 ≤ h ≤ l o g ⌈ m / 2 ⌉ n + 1 2 + 1 log_m{n+1}≤h≤log_{⌈m/2⌉}\frac {n+1}2+1 logmn+1≤h≤log⌈m/2⌉2n+1+1
7.3.2. B树的基本操作
- B树的查找:B树的查找操作与二叉查找树类似。B树的查找包含两个基本操作:① 在B树中找结点;② 在结点中找关键字。B树常存储在磁盘上,因此前一个查找操作在磁盘上进行,后一个查找操作在内存中进行。在B树中查找到某个结点后,先在有序表中进行查找,若找到则查找成功,否则按照对应指针信息到所指的子树中去查找。查找到叶子结点(对应指针为空指针),则说明树中没有对应的关键字,查找失败。
- B树的插入:将关键字 key 插入到B树的过程:
- 定位:利用B树的查找算法,找到插入该关键字的最底层中的某个非叶子结点。(插入位置一定是最底层的某个非叶子结点!)
- 插入:B树中,每个非失败节点的关键字个数都在区间 [ ⌈ m / 2 ⌉ − 1 , m − 1 ] [⌈m/2⌉- 1,m-1] [⌈m/2⌉−1,m−1]内。若插入关键字 key 之后结点关键字个数小于m,则可以直接插入;否则必须对结点进行分裂。
- 分裂:从结点的中间位置( ⌈ m / 2 ⌉ ⌈m/2⌉ ⌈m/2⌉)将其中的关键字分为两部分,左半部分包含的关键字放到原结点中,右半部分包含的关键字放到新节点中,中间位置( ⌈ m / 2 ⌉ ⌈m/2⌉ ⌈m/2⌉)的关键字则插入原节点的父节点。若此时父节点的关键字也超过了上限,则对父节点继续进行分裂操作,直到这个过程传到根节点为止,进而导致B树的高度增加。

- B树的删除:
- 非终端结点的删除:使用直接前驱或者直接后继来代替被删除的关键字,转换为删除终端结点。
- 终端结点的删除,具体分为三种情况:
- 直接删除关键字:若删除关键字所在结点关键字个数 ≥ ⌈ m / 2 ⌉ ≥⌈m/2⌉ ≥⌈m/2⌉,则可直接删除。
- 兄弟够借:若删除关键字所在结点关键字个数 = ⌈ m / 2 ⌉ − 1 =⌈m/2⌉-1 =⌈m/2⌉−1,且与此结点相邻的左(或右)兄弟结点关键字个数 ≥ ⌈ m / 2 ⌉ ≥⌈m/2⌉ ≥⌈m/2⌉,则需调整该节点、左(或右)兄弟结点及其双亲结点(父子换位法)以达到新的平衡。
- 兄弟不够接:若删除关键字所在结点关键字个数 = ⌈ m / 2 ⌉ − 1 =⌈m/2⌉-1 =⌈m/2⌉−1,且与此结点相邻的左(或右)兄弟结点关键字个数 = ⌈ m / 2 ⌉ − 1 =⌈m/2⌉-1 =⌈m/2⌉−1,则将该节点、左(或右)兄弟结点及其双亲结点中的关键字进行合并。

7.3.3. B+树
- 一棵m阶的B+树需满足以下条件:
- 每个分支节点最多有m棵子树(孩子结点)。
- 非叶根结点至少有两颗子树,其他每个分支结点至少有 ⌈ m / 2 ⌉ ⌈m/2⌉ ⌈m/2⌉棵子树。
- 结点的子树个数与关键字个数相同。
- 所有叶子结点包含所有关键字及指向相应记录的指针,叶子结点中将关键字按大小排列,并且相邻叶子结点按大小顺序相互链接起来。(说明B+树支持顺序查找)
- 所有分支节点仅包含它的各个节点中关键字的最大值及指向其子节点的指针。

- 对比 B树:
| m阶B树 | m阶B+树 |
|---|---|
| 结点中n个关键字对应n+1棵子树 | 结点中n个关键字对应n棵子树 |
| 根节点关键字数n
∈
[
1
,
m
−
1
]
∈[1,m-1]
∈[1,m−1] 其他结点关键字数n ∈ [ ⌈ m / 2 ⌉ − 1 , m − 1 ] ∈[⌈m/2⌉-1,m-1] ∈[⌈m/2⌉−1,m−1] |
根节点关键字数n
∈
[
1
,
m
]
∈[1,m]
∈[1,m] 其他结点关键字数n ∈ [ ⌈ m / 2 ⌉ , m ] ∈[⌈m/2⌉,m] ∈[⌈m/2⌉,m] |
| 各结点包含的关键字是不重复的 | 叶子结点包含全部关键字,非叶结点出现过的关键字也会出现在叶子结点中 |
| 结点中包含了关键字对应的记录的存储地址 | 叶子结点包含信息,非叶结点只起索引作用。非叶结点中的每个索引项只含有对应子树的最大关键字和指向该字树的指针,不含有该关键字对应记录的存储地址 |
| 不支持顺序查找。查找成功时可能停在任何一层结点,查找速度不稳定 | 支持顺序查找。查找成功或失败一定会达到最下一层结点,查找速度稳定 |
7.4. 散列查找及其性能分析
7.4.1. 散列表的基本概念
- 散列函数:一个把查找表中的关键字映射成该关键字对应的地址的函数,记作 H a s h ( k e y ) = A d d r Hash(key)=Addr Hash(key)=Addr。
- 散列函数可能会把两个或两个以上的不同关键字映射到同一地址,称这种情况为冲突。发生碰撞的不同关键字称为同义词。
- 散列表:根据关键字而直接进行访问的数据结构。散列表建立了关键字和存储地址之间的一种直接映射关系。
7.4.2. 散列函数的构造方法
-
直接定址法:直接取关键字的某个线性函数值为散列地址,散列函数为 H ( k e y ) = k e y H(key)=key H(key)=key 或 H ( k e y ) = a × k e y + b H(key)=a×key+b H(key)=a×key+b。这种方法计算简单,不会产生冲突。缺点是空位较多,会造成存储空间浪费。
-
除留余数法:假定散列表表长 m,取一个不大于但最接近 m 的质数 p,利用散列函数 H ( k e y ) = k e y % p H(key)=key\%p H(key)=key%p 将关键字转换为散列地址。p取质数是因为这样可以使关键字通过散列函数转换后等概率地映射到散列空间上的任一地址。
-
数字分析法:假设关键字是 r进制数,而r个数码在个位上出现的频率不一定相同,可能在某些位上分布的均匀一些,而在某些位分布的不均匀。此时应选数码分布均匀的若干位作为散列地址。
-
平方取中法:这种方法取关键字平方值的中间几位作为散列地址,具体取多少位视具体情况而定。这种方法得到的散列地址与关键字的每一位都有关系,因此使得散列地址分布比较均匀。适用于关键字每位取值都不够均匀或均小于散列地址所需的位数。
7.4.3. 处理冲突的方法
-
开放定址法:指可存放新表项的空闲抵制既向它的同义词表项开放,又向它的非同义词表项开放。其数学递推公式为:
H i = ( H ( k e y ) + d i ) % m H_i=(H(key)+d_i)\%m Hi=(H(key)+di)%m
其中, H ( k e y ) H(key) H(key)为散列函数, i = 0 , 1 , 2 , . . . , k ( k ≤ m − 1 ) i=0,1,2,...,k(k≤m-1) i=0,1,2,...,k(k≤m−1),m表示散列表表长, d i d_i di为增量序列。增量序列通常有四种取法:- 线性探测法: d i = 0 , 1 , 2 , . . . , m − 1 d_i=0,1,2,...,m-1 di=0,1,2,...,m−1。使用方法发生冲突时,顺序查看下一个单元,直到找到一个空闲单元或查遍全表。使用这种方法可能造成大量元素在相邻的散列地址上堆积起来,大大降低了查找效率。使用这种方法删除元素时需要做标记,否则会影响查找元素。
- 平方探测法: d i = 0 2 , 1 2 , − 1 2 , 2 2 , − 2 2 , . . . , k 2 , − k 2 d_i=0^2,1^2,-1^2,2^2,-2^2,...,k^2,-k^2 di=02,12,−12,22,−22,...,k2,−k2。其中 k ≤ m / 2 k≤m/2 k≤m/2,散列表长度m必须是一个可以表示为 4 k + 3 4k+3 4k+3 的质数(符合这个条件才能够探测到所有位置)。使用这种方法可以避免堆积问题。
- 再散列法: d i = H 2 ( k e y ) d_i=H_2(key) di=H2(key)。当通过第一个散列函数 H ( k e y ) H(key) H(key) 得到的地址发生冲突时,则利用第二个散列函数 H 2 ( k e y ) H_2(key) H2(key) 再次计算该关键字的地址。其散列函数为: H i = R H i ( k e y ) H_i=RH_i(key) Hi=RHi(key)。
- 伪随机序列法: d i = d_i= di= 伪随机序列。
-
拉链法:对于不同的关键字通过散列函数映射到同一地址时,为了与避免非同义词发生冲突,可以把所有的同义词存储到一个线性链表中。拉链法适用于经常进行插入和删除的方法。

7.4.4. 散列查找及性能分析
- 散列查找执行步骤如下:
- 初始化: A d d r = H a s h ( k e y ) Addr=Hash(key) Addr=Hash(key)
- 检测查找表中地址为 Addr 的位置上是否有记录,若无记录,返回查找失败;若有记录,比较它和 key 的值,若相等则返回查找成功,否则执行步骤③。
- 用给定的处理冲突方式计算“下一个散列表地址”,并把 Addr 置为此地址,转入步骤②。
- 平均查找长度(ASL):散列表查找成功的平均查找长度即找到表中已有表项的平均比较次数;散列表查找失败的平均查找长度即找不到待查的表项但能找到插入位置的平均比较次数。
-
例:现有长度为11且初始为空的散列表HT,散列函数 H ( k e y ) = k e y % 7 H(key) = key \% 7 H(key)=key%7,采用线性探查法解决冲突。将关键字序列87,40,30,6,11,22,98,20 ,38依次插入HT后,HT的查找失败的平均长度是多少? 查找成功的平均查找长度又是多少?
答:关键字序列依次插入后,散列表HT如下所示:
| 散列地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 98 | 22 | 30 | 87 | 11 | 40 | 6 | 20 | 38 | ||
| 冲突次数 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 5 |
A S L 查 找 成 功 = ( 1 + 1 + 1 + 1 + 1 + 1 + 1 + 2 + 6 ) / 9 = 5 / 3 ASL_{查找成功}=(1+1+1+1+1+1+1+2+6)/9=5/3 ASL查找成功=(1+1+1+1+1+1+1+2+6)/9=5/3
A S L 查 找 失 败 = ( 10 + 9 + 8 + 7 + 6 + 5 + 4 ) / 7 = 7 ASL_{查找失败}=(10+9+8+7+6+5+4)/7=7 ASL查找失败=(10+9+8+7+6+5+4)/7=7
- 装填因子:一般计为 α \alpha α,即一个表的装满程度。 α = 表 中 记 录 数 n 散 列 表 长 度 m \alpha=\frac{表中记录数n}{散列表长度m} α=散列表长度m表中记录数n
八、排序
8.1. 排序的基本概念
- 排序:重新排列表中的元素,使表中元素满足按关键字有序的过程。
- 输入:n个记录 R 1 , R 2 , . . . , R n R_1,R_2,...,R_n R1,R2,...,Rn,对应的关键字为 k 1 , k 2 , . . . , k n k_1,k_2,...,k_n k1,k2,...,kn。
- 输出:输入序列的一个重排 R 1 ′ , R 2 ′ , . . . , R n ′ R_1',R_2',...,R_n' R1′,R2′,...,Rn′,使得 k 1 ′ ≤ k 2 ′ ≤ . . . ≤ k n ′ k_1'≤k_2'≤...≤k_n' k1′≤k2′≤...≤kn′。
- 算法的稳定性:关键字相同的元素在使用某一排序算法之后相对位置不变,则称这个排序算法是稳定的,否则称其为不稳定的。稳定的排序算法不一定比不稳定的排序算法要好。
- 排序算法的评价指标:时间复杂度、空间复杂度、稳定性。
- 排序算法的分类:
内部排序: 排序期间元素都在内存中——关注如何使时间、空间复杂度更低。
外部排序: 排序期间元素无法全部同时存在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动——关注如何使时间、空间复杂度更低,如何使读/写磁盘次数更少。
8.2. 插入排序
8.2.1. 直接插入排序
- 算法思想:每次将一个待排序的记录按其关键字大小,插入到前面已经排好序的子序列中,直到全部记录插入完成。
- 代码实现(不带哨兵):
// 对A[]数组中共n个元素进行插入排序
void InsertSort(int A[],int n){
int i,j,temp;
for(i=1; i<n; i++){
if(A[i]<A[i-1]){ //如果A[i]关键字小于前驱
temp=A[i];
for(j=i-1; j>=0 && A[j]>temp; --j)
A[j+1]=A[j]; //所有大于temp的元素都向后挪
A[j+1]=temp;
}
}
}
- 代码实现(带哨兵):
// 对A[]数组中共n个元素进行插入排序
void InsertSort(int A[], int n){
int i,j;
for(i=2; i<=n; i++){
if(A[i]<A[i-1]){
A[0]=A[i]; //复制为哨兵,A[0]不放元素
for(j=i-1; A[0]<A[j]; --j)
A[j+1]=A[j];
A[j+1]=A[0];
}
}
}
- 算法效率分析:
- 时间复杂度:最好情况 O ( n ) O(n) O(n),最差情况 O ( n 2 ) O(n^2) O(n2),平均情况 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
- 算法稳定性:稳定。
- 适用性:适用于顺序存储和链式存储的线性表。
- 对链表进行插入排序:
//对链表L进行插入排序
void InsertSort(LinkList &L){
LNode *p=L->next, *pre;
LNode *r=p->next;
p->next=NULL;
p=r;
while(p!=NULL){
r=p->next;
pre=L;
while(pre->next!=NULL && pre->next->data<p->data)
pre=pre->next;
p->next=pre->next;
pre->next=p;
p=r;
}
}
8.2.2. 折半插入排序
- 算法思路: 每次将一个待排序的记录按其关键字大小,使用折半查找找到前面子序列中应该插入的位置并插入,直到全部记录插入完成。
- 注意:为了保证稳定性,当查找到和插入元素关键字一样的元素时,应该在这个元素的右半部分继续查找以确认位置。即当 A[mid] == A[0] 时,应继续在mid所指位置右边寻找插入位置。
- 代码实现:
//对A[]数组中共n个元素进行折半插入排序
void InsertSort(int A[], int n){
int i,j,low,high,mid;
for(i=2; i<=n; i++){
A[0]=A[i]; //将A[i]暂存到A[0]
low=1; high=i-1;
while(low<=high){ //折半查找
mid=(low+high)/2;
if(A[mid]>A[0])
high=mid-1;
else
low=mid+1;
}
for(j=i-1; j>high+1; --j)
A[j+1]=A[j];
A[high+1]=A[0];
}
}
- 与直接插入排序相比,比较关键字的次数减少了,但是移动元素的次数没有变。时间复杂度仍为 O ( n ² ) O(n²) O(n²)
8.2.3. 希尔排序
- 算法思路:先追求表中元素的部分有序,再逐渐逼近全局有序,以减小插入排序算法的时间复杂度。
- 具体实施:先将待排序表分割成若干形如 L [ i , i + d , i + 2 d , . . . , i + k d ] L[i,i+d,i+2d,...,i+kd] L[i,i+d,i+2d,...,i+kd] 的“特殊”子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到 d=1 为止。
- 代码实现:
// 对A[]数组共n个元素进行希尔排序
void ShellSort(ElemType A[], int n){
int d,i,j;
for(d=n/2; d>=1; d=d/2){ //步长d递减
for(i=d+1; i<=n; ++i){
if(A[i]<A[i-d]){
A[0]=A[i]; //A[0]做暂存单元,不是哨兵
for(j=i-d; j>0 && A[0]<A[j]; j-=d)
A[j+d]=A[j];
A[j+d]=A[0];
}
}
}
}
- 算法效率分析:
- 时间复杂度:希尔排序时间复杂度依赖于增量序列的函数。最差情况 O ( n 2 ) O(n^2) O(n2),n在某个特顶范围时可达 O ( n 1.3 ) O(n^{1.3}) O(n1.3)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
- 算法稳定性:不稳定。
8.3. 交换排序
8.3.1. 冒泡排序
-
算法思路:从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即 A [ i − 1 ] > A [ i ] A[i-1]>A[i] A[i−1]>A[i]),则交换它们,直到序列比较完。如此重复最多 n-1 次冒泡就能将所有元素排好序。为保证稳定性,关键字相同的元素不交换。
-
代码实现:
// 交换a和b的值
void swap(int &a, int &b){
int temp=a;
a=b;
b=temp;
}
// 对A[]数组共n个元素进行冒泡排序
void BubbleSort(int A[], int n){
for(int i=0; i<n-1; i++){
bool flag = false; //标识本趟冒泡是否发生交换
for(int j=n-1; j>i; j--){
if(A[j-1]>A[j]){
swap(A[j-1],A[j]);
flag=true;
}
}
if(flag==false)
return; //若本趟遍历没有发生交换,说明已经有序
}
}
- 算法效率分析:
- 时间复杂度:最好情况 O ( n ) O(n) O(n),最差情况 O ( n 2 ) O(n^2) O(n2),平均情况 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
- 稳定性:稳定。
- 适用性:冒泡排序可以用于顺序表、链表。
8.3.2. 快速排序
- 算法思路:在待排序表 L [ 1... n ] L[1...n] L[1...n] 中任选一个元素 pivot 作为枢轴(通常取首元素),通过一趟排序将待排序表分为独立的两部分 L [ 1... k − 1 ] L[1...k-1] L[1...k−1] 和 L [ k − 1... n ] L[k-1...n] L[k−1...n]。使得 L [ 1... k − 1 ] L[1...k-1] L[1...k−1] 中的所有元素小于 pivot, L [ k − 1... n ] L[k-1...n] L[k−1...n] 中的所有元素大于等于 pivot,则 pivot 放在了其最终位置 L [ k ] L[k] L[k] 上。重复此过程直到每部分内只有一个元素或空为止。
- 快速排序是所有内部排序算法中性能最优的排序算法。
- 在快速排序算法中每一趟都会将枢轴元素放到其最终位置上。(可用来判断进行了几趟快速排序)
- 快速排序可以看作数组中n个元素组织成二叉树,每趟处理的枢轴是二叉树的根节点,递归调用的层数是二叉树的层数。
- 代码实现:
// 用第一个元素将数组A[]划分为两个部分
int Partition(int A[], int low, int high){
int pivot = A[low];
while(low<high){
while(low<high && A[high]>=pivot)
--high;
A[low] = A[high];
while(low<high && A[low]<=pivot)
++low;
A[high] = A[low];
}
A[low] = pivot;
return low;
}
// 对A[]数组的low到high进行快速排序
void QuickSort(int A[], int low, int high){
if(low<high){
int pivotpos = Partition(A, low, high); //划分
QuickSort(A, low, pivotpos - 1);
QuickSort(A, pivotpos + 1, high);
}
}
- 算法效率分析:
- 时间复杂度:快速排序的时间复杂度 = O ( n × 递 归 调 用 的 层 数 ) O(n×递归调用的层数) O(n×递归调用的层数)。最好情况 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n),最差情况 O ( n 2 ) O(n^2) O(n2),平均情况 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度:快速排序的空间复杂度 = O ( 递 归 调 用 的 层 数 ) O(递归调用的层数) O(递归调用的层数)。最好情况 O ( l o g 2 n ) O(log_2n) O(log2n),最差情况 O ( n ) O(n) O(n),平均情况 O ( n 2 ) O(n^2) O(n2)。
- 稳定性:不稳定。
8.4. 选择排序
选择排序思想: 每一趟在待排序元素中选取关键字最小(或最大)的元素加入有序子序列。
8.4.1. 简单选择排序
- 算法思路:每一趟在待排序元素中选取关键字最小的元素与待排序元素中的第一个元素交换位置。
- 代码实现:
// 交换a和b的值
void swap(int &a, int &b){
int temp = a;
a = b;
b = temp;
}
// 对A[]数组共n个元素进行选择排序
void SelectSort(int A[], int n){
for(int i=0; i<n-1; i++){ //一共进行n-1趟,i指向待排序序列中第一个元素
int min = i;
for(int j=i+1; j<n; j++){ //在A[i...n-1]中选择最小的元素
if(A[j]<A[min])
min = j;
}
if(min!=i)
swap(A[i], A[min]);
}
}
- 算法效率分析:
- 时间复杂度:无论待排序序列有序、逆序还是乱序,都需要进行 n-1 次处理,总共需要对比关键字 ( n − 1 ) + ( n − 2 ) + . . . + 1 = n ( n − 1 ) / 2 (n-1)+(n-2)+...+1= n(n-1)/2 (n−1)+(n−2)+...+1=n(n−1)/2 次,因此时间复杂度始终是 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
- 稳定性:不稳定。
- 适用性:适用于顺序存储和链式存储的线性表。
- 对链表进行简单选择排序:
void selectSort(LinkList &L){
LNode *h=L,*p,*q,*r,*s;
L=NULL;
while(h!=NULL){
p=s=h; q=r=NULL;
while(p!=NULL){
if(p->data>s->data){
s=p; r=q;
}
q=p; p=p->next;
}
if(s==h)
h=h->next;
else
r->next=s->next;
s->next=L; L=s;
}
}
8.4.2. 堆排序
- 什么是堆(Heap)?:可理解为一棵顺序存储的完全二叉树。
- 大根堆:完全二叉树中,根 ≥ 左右,即 L [ i ] ≥ L [ 2 i ] L[i]≥L[2i] L[i]≥L[2i] 且 L [ i ] ≥ L [ 21 + 1 ] L[i]≥L[21+1] L[i]≥L[21+1]
- 小根堆:完全二叉树中,根 ≤ 左右,即 L [ i ] ≤ L [ 2 i ] L[i]≤L[2i] L[i]≤L[2i] 且 L [ i ] ≤ L [ 21 + 1 ] L[i]≤L[21+1] L[i]≤L[21+1]( 1 ≤ i ≤ ⌊ n / 2 ⌋ 1≤i≤\lfloor n/2 \rfloor 1≤i≤⌊n/2⌋)

-
算法思路:首先将存放在 L [ 1... n ] L[1...n] L[1...n] 中的n个元素建成初始堆,由于堆本身的特点,堆顶元素就是最大值。将堆顶元素与堆底元素交换,这样待排序列的最大元素已经找到了排序后的位置。此时剩下的元素已不满足大根堆的性质,堆被破坏,将堆顶元素下坠使其继续保持大根堆的性质,如此重复直到堆中仅剩一个元素为止。
-
在顺序存储的完全二叉树中:
- 非终端结点的编号 : i ≤ ⌊ n / 2 ⌋ i≤⌊n/2⌋ i≤⌊n/2⌋
- i 的左右孩子 : 2 i 2i 2i 和 2 i + 1 2i+1 2i+1
- i 的父节点: ⌊ i / 2 ⌋ ⌊i/2⌋ ⌊i/2⌋
-
代码实现:
// 对初始序列建立大根堆
void BuildMaxHeap(int A[], int len){
for(int i=len/2; i>0; i--) //从后往前调整所有非终端结点
HeadAdjust(A, i, len);
}
// 将以k为根的子树调整为大根堆
void HeadAdjust(int A[], int k, int len){
A[0] = A[k];
for(int i=2*k; i<=len; i*=2){ //沿k较大的子结点向下调整
if(i<len && A[i]<A[i+1])
i++;
if(A[0] >= A[i])
break;
else{
A[k] = A[i]; //将A[i]调整至双亲结点上
k=i; //修改k值,以便继续向下筛选
}
}
A[k] = A[0]
}
// 交换a和b的值
void swap(int &a, int &b){
int temp = a;
a = b;
b = temp;
}
// 对长为len的数组A[]进行堆排序
void HeapSort(int A[], int len){
BuildMaxHeap(A, len); //初始建立大根堆
for(int i=len; i>1; i--){ //n-1趟的交换和建堆过程
swap(A[i], A[1]);
HeadAdjust(A,1,i-1);
}
}
-
算法效率分析:
- 时间复杂度: O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)。建堆时间 O ( n ) O(n) O(n),之后进行 n-1 次向下调整操作,每次调整时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
- 稳定性:不稳定。
-
堆的插入:对于大(或小)根堆,要插入的元素放到表尾,然后与父节点对比,若新元素比父节点更大(或小),则将二者互换。新元素就这样一路==“上升”==,直到无法继续上升为止。
-
堆的删除:被删除的元素用堆底元素替换,然后让该元素不断==“下坠”==,直到无法下坠为止。
8.5. 归并排序和基数排序
8.5.1. 归并排序
- 归并(Merge):把两个或多个已经有序的序列合并成一个新的有序表。k路归并每选出一个元素,需对比关键字k-1次。

- 算法思想:把待排序表看作 n 个有序的长度为1的子表,然后两两合并,得到 ⌈ n / 2 ⌉ \lceil n/2\rceil ⌈n/2⌉ 个长度为2或1的有序表……如此重复直到合并成一个长度为n的有序表为止。
- 代码实现:
// 辅助数组B
int *B=(int *)malloc(n*sizeof(int));
// A[low,...,mid],A[mid+1,...,high]各自有序,将这两个部分归并
void Merge(int A[], int low, int mid, int high){
int i,j,k;
for(k=low; k<=high; k++)
B[k]=A[k];
for(i=low, j=mid+1, k=i; i<=mid && j<= high; k++){
if(B[i]<=B[j])
A[k]=B[i++];
else
A[k]=B[j++];
}
while(i<=mid)
A[k++]=B[i++];
while(j<=high)
A[k++]=B[j++];
}
// 递归操作
void MergeSort(int A[], int low, int high){
if(low<high){
int mid = (low+high)/2;
MergeSort(A, low, mid);
MergeSort(A, mid+1, high);
Merge(A,low,mid,high); //归并
}
}
- 算法效率分析:算法效率分析:
- 时间复杂度:每趟归并时间复杂度 O ( n ) O(n) O(n),需要进行 ⌈ l o g 2 n ⌉ \lceil log_2n\rceil ⌈log2n⌉趟归并(将归并过程看作倒立的二叉树),所以时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)。
- 空间复杂度: O ( n ) O(n) O(n)。
- 稳定性:稳定。
8.5.2. 基数排序
- 算法思想:把整个关键字拆分为d位,按照各个关键字位递增的次序(比如:个、十、百),做d趟“分配”和“收集”,若当前处理关键字位可能取得r个值,则需要建立r个队列。
- 分配:顺序扫描各个元素,根据当前处理的关键字位,将元素插入相应的队列。一趟分配耗时 O ( n ) O(n) O(n)。
- 收集:把各个队列中的结点依次出队并链接。一趟收集耗时 O ( r ) O(r) O(r)。

- 基数排序擅长处理的问题:
- 数据元素的关键字可以方便地拆分为d组,且d较小。
- 每组关键字的取值范围不大,即r较小。
- 数据元素个数n较大。
- 算法效率分析:算法效率分析:
- 时间复杂度:一共进行d趟分配收集,一趟分配需要 O ( n ) O(n) O(n),一趟收集需要 O ( r ) O(r) O(r),时间复杂度为 O [ d ( n + r ) ] O[d(n+r)] O[d(n+r)],且与序列的初始状态无关.
- 空间复杂度: O ( r ) O(r) O(r),其中r为辅助队列数量。
- 稳定性:稳定。
8.6. 内部排序算法总结
8.6.1. 内部排序算法比较
| 算法种类 | 最好时间复杂度 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 冒泡排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 简单选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 希尔排序 | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 | ||
| 快速排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n 2 ) O(n^2) O(n2) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | 不稳定 |
| 堆排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 2路归并排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n ) O(n) O(n) | 稳定 |
| 基数排序 | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( r ) O(r) O(r) | 稳定 |
8.6.2. 内部排序算法的应用
- 选取排序方法需要考虑的因素:
- 待排序的元素数目n。
- 元素本身信息量的大小。
- 关键字的结构及其分布情况。
- 稳定性的要求。
- 语言工具的条件,存储结构及辅助空间的大小等。
- 排序算法的选择:
- 若n较小,可采用 直接插入排序 或 简单选择排序。由于直接插入排序所需的记录移动次数较简单选择排序的多,因而当记录本身信息量较大时,用简单选择排序较好。
- 若文件的初始状态已按关键字基本有序,则选用直接插入排序或冒泡排序为宜。
- 若n较大,则应采用时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) 的排序方法:快速排序、堆排序 或 归并排序。快速排序被认为是目前基于比较的内部排序方法中最好的方法,当待排序的关键字随机分布时,快速排序的平均时间最短。堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况,这两种排序都是不稳定的。若要求排序稳定且时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n),则可选用归并排序。但本章介绍的从单个记录起进行两两归并的排序算法并不值得提倡,通常可以将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子文件,然后两两归并。直接插入排序是稳定的,因此改进后的归并排序仍是稳定的。
- 在基于比较的排序方法中,每次比较两个关键字的大小之后,仅出现两种可能的转移,因此可以用一棵二叉树来描述比较判定过程,由此可以证明:当文件的n个关键字随机分布时,任何借助于“比较”的排序算法,至少需要 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) 的时间。
- 若n很大,记录的关键字位数较少且可以分解时,采用 基数排序 较好。
- 当记录本身信息量较大时,为避免耗费大量时间移动记录,可用链表作为存储结构。
8.7. 外部排序
8.7.1. 外部排序的基本概念和方法
- 外部排序:对大文件进行排序时,因为文件中的记录很多、信息量庞大,无法将整个文件复制进内存中进行排序。因此需要将待排序的记录存储在外存上,排序时再把数据一部分一部分地调入内存进行排序,在排序过程中需要多次进行内存和外存之间的交换。
- 外部排序的步骤:① 跟据内存缓冲区大小,将外存上的文件分成 r 个子文件,依次读入内存并利用内部排序方法对它们进行排序,并将排序后得到的有序子文件重新写回外存(归并段)。② 对这些归并段进行 S 趟 k 路归并,使归并段(有序子文件)逐渐由小到大,直至得到整个有序文件为止,其中 S = ⌈ l o g k r ⌉ S=\lceil log_kr\rceil S=⌈logkr⌉。(需要在内存中分配k个输入缓冲区和1个输出缓冲区)
- 如何进行 k 路归并:① 把k个归并段的块读入k个输入缓冲区。 ② 用“归并排序”的方法从k个归并段中选出几个最小记录暂存到输出缓冲区中。 ③ 当输出缓冲区满时,写出外存。
- 外部排序时间开销 = 读写外存的时间 + 内部排序所需时间+内部归并所需时间
- 优化:
- 增加归并路数k,但是需要增加相应的输入缓冲区,且每次从k个归并段中选出一个最小元素需要对比 (k-1) 次。
- 减少初始归并段数量r。
8.7.2. 败者树
- 败者树解决的问题:使用多路平衡归并可以减少归并趟数,但是从 k 个归并段选出一个最小元素需要对比关键字 (k-1) 次,构造败者树可以使关键字对比次数减少到 ⌈ l o g 2 k ⌉ \lceil log_2k\rceil ⌈log2k⌉。
- 败者树可视为一棵完全二叉树(多了一个头头)。k个叶结点分别对应k个归并段中当前参加比较的元素,非叶子结点用来记忆左右子树中的“失败者”,而让胜者往上继续进行比较,一直到根结点。

8.7.3. 置换-选择排序(生成初始归并段)
-
置换-选择排序:产生更长的初始归并段,从而减少初始归并段数量。
-
设初始待排文件为FI,初始归并段输出文件为FO,内存工作区为WA,FO和WA的初始状态为空,WA可容纳w个记录。
置换-选择算法的步骤如下:文章来源:https://www.toymoban.com/news/detail-780144.html
- 从FI输入w个记录到工作区WA。
- 从WA中选出其中关键字取最小值的记录,记为MINIMAX记录。
- 将MINIMAX记录输出到FO中去。
- 若FI不空,则从FI输入下一个记录到WA中。
- 从WA中所有关键字比MINIMAX记录的关键字大的记录中选出最小关键字记录,作为新的MINIMAX记录。
- 重复③~⑤,直至在WA中选不出新的MINIMAX记录为止,由此得到一个初始归并段,输出一个归并段的结束标志到FO中去。
- 重复②~⑥,直至WA为空。由此得到全部初始归并段。
 文章来源地址https://www.toymoban.com/news/detail-780144.html
文章来源地址https://www.toymoban.com/news/detail-780144.html
8.7.4. 最佳归并树
- 最佳归并树:调整多个初始归并段进行多路归并时的顺序,从而减少多路归并时I/O次数。
- 理论基础:每个初始归并段对应一个叶子结点,把归并段的块数作为叶子的权值,归并树的WPL = 树中所有叶结点的带权路径长度之和。归并过程中的磁盘I/O次数 = 归并树的WPL * 2。
- 注意:k叉归并的最佳归并树一定是严格k叉树,即树中只有度为k、度为0的结点。
- 构造k叉哈夫曼树:每次选择k个根节点权值最小的树合并,并将k个根节点的权值之和作为新的根节点的权值。
- 补充虚段:
- 若 ( 初 始 归 并 段 数 量 − 1 ) % ( k − 1 ) = 0 (初始归并段数量-1)\%(k-1)=0 (初始归并段数量−1)%(k−1)=0,说明刚好可以构成严格k叉树,此时不需要添加虚段。
- 若 ( 初 始 归 并 段 数 量 − 1 ) % ( k − 1 ) = u ≠ 0 (初始归并段数量-1)\%(k-1)=u≠0 (初始归并段数量−1)%(k−1)=u=0,则需要补充 ( k − 1 ) − u (k-1) - u (k−1)−u 个虚段。
到了这里,关于数据结构学习笔记(王道)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!