统计学习笔记：方差分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了统计学习笔记：方差分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

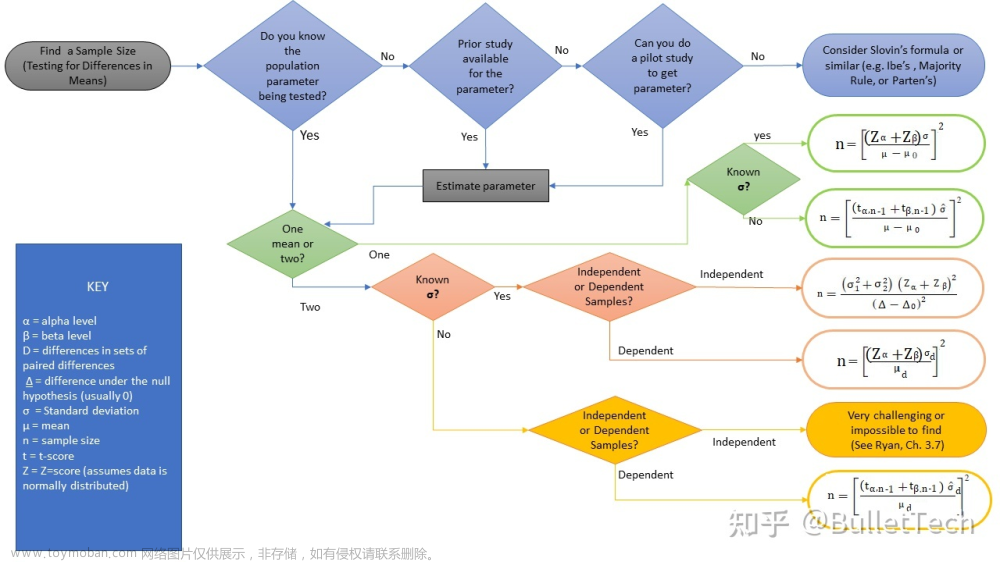
方差分析（ANOVA）又称F检验。方差分析是判定方差在组间和组内是否（明显）具有区别的一种方法。如果组内差异相对于组间差异较小，则可以推断出组与组之间是有明显差异的。
从形式上看，方差分析与t检验或z检验区别不大，都是检验均值是否相等，但方差分析可以同时比较多个均值。
广义的方差分析分为：

单因素方差分析（1-way ANOVA）
双因素方差分析（2-way ANOVA）与多因素方差分析（N-way ANOVA）
协方差分析（ANCOVA）
多响应方差分析（MANOVA）
重复测量（Repeated Measures）

在这里主要介绍单因素方差分析（1-way ANOVA）。

基本思想

首先要说明的是，方差分析一共有三大前提假设：

各组样本背后所隐含的族群分布必须为正态分布或者是逼近正态分布。
各组样本必须独立。
族群的方差必须相等。

方差分析的核心思想一句话：“所有样本的总差异可以分解为组间差异和组内差异”，即SST=SSR+SSE。 $i$ 为组别 $（ i = 1, 2..., I ）$ ， $j$ 为观测值个数 $（ j = 1, 2, 3, ..., J ）$ ， $Y_{ij}$ 为第 $i$ 组第 $j$ 个观测值， $\overline Y_{Total}$ 为所有观测值的平均数。

总差异（SST）：全部样本与全体样本均值的总差异， $\sum_i\sum_j(Y_{ij}-\overline Y_{Total})^2$ ，总差异的自由度为N-1。
组间差异（SSR）：组均值与总体均值的差异， $\sum_in_i(\bar Y_j-\overline Y_{Total})^2$ ，组间差异的自由度为k-1。
组内差异（SSE）：具体每个样本与其所在组均值的差异， $\sum_i\sum_j(Y_{ij}-\overline Y_{j})^2$ ，组内差异的自由度为N-k。

F检验的零假设认为所有组的均值都相等，备择假设则认为所有组的均值不全相等（即至少有一个组的均值与其它具有显著差异），如下：
$H_0:\mu_1=\mu_2=...=\mu_n\\ H_1:所有组的均值不全相等$
我们要通过SSR与SSE除以各自的自由度，得到MSR和MSE，MSR和MSE的比值就是F统计量：
$F=\frac{SSR/k-1}{SSE/N-k}=\frac{MSR}{MSE}\sim F_{k-1,N-k}$
当H0成立时，F统计量服从对应自由度分别为k-1，N-k的F分布。F值越接近1，就越没有理由拒绝H0；反之，F值越大，拒绝H0的理由就越充分。

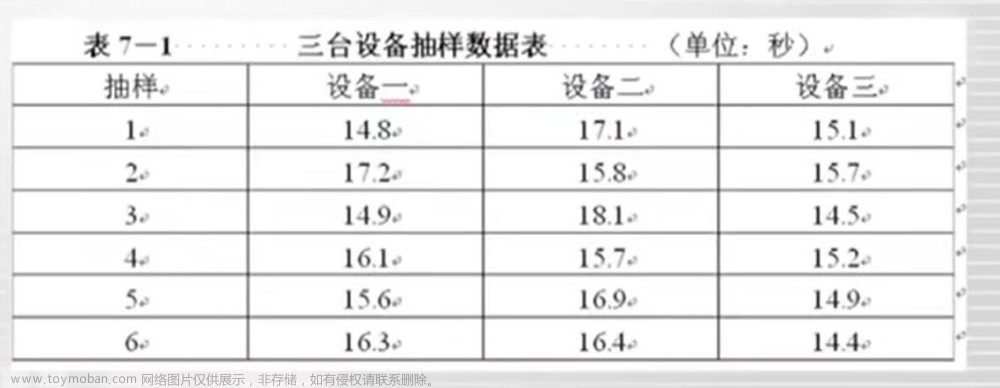
实例

方差分析组内和组间差异,学习,python,概率论

计算总均值： $\overline Y_{Total}=1.626$
计算分组均值： $\overline Y_1=1.674$ ， $\overline Y_2=1.598$ ， $\overline Y_3=1.649$ ， $\overline Y_4=1.562$ 。
计算组内差异： $SSE=\sum_i\sum_j(Y_{ij}-\overline Y_{j})^2=0.167$
计算组间差异： $SSR=\sum_in_i(\bar Y_j-\overline Y_{Total})^2=0.049$
计算F统计量： $F=\frac{SSR/k-1}{SSE/N-k}=\frac{0.049/3}{0.167/22}\approx2.17$

参考F统计量表， $P (F > 3.05) = 0.05$ ，在95%置信水平上临界值为3.05。2.17<3.05，所以没有理由拒绝原假设。所以认为这四组数据的均值无显著差异。

Python实现

from scipy import stats

A1 = [1.6, 1.61, 1.65, 1.68, 1.7, 1.7, 1.78]
A2 = [1.5, 1.64, 1.4, 1.7, 1.75]
A3 = [1.64, 1.55, 1.6, 1.62, 1.64, 1.60, 1.74, 1.8]
A4 = [1.51, 1.52, 1.53, 1.57, 1.64, 1.6]

data = [A1, A2, A3, A4]
f, p = stats.f_oneway(*data)
print(f, p)