南昌航空大学实验报告
课程名称: 数据结构A 实验名称: 实验五 稀疏矩阵运算
班 级: XXX 学生姓名: XXX 学号: XXXXX
指导教师评定: XXX 签 名: XXX
一、实验目的
数组是一种常用的数据类型,本实验是有关两个稀疏矩阵进行相加的应用。
通过对本实验的学习,可以理解矩阵的相关操作方法。
二、实验内容
在本实验的实例程序中,假设两个稀疏矩阵A和B,它们均为m行n列,要求编写求矩阵的加法即C=A+B的算法(C矩阵存放A与B相加的结果)。
三、程序分析
我们利用一维数组来存储。一维数组顺序存放非零元素的行号、列号和数值,行号-1作为结束标志。然后在进行矩阵加法运算时依次扫描矩阵A和B的行列值,并以行优先。当行列相同时,将第三个元素值相加的和以及行列号三个元素存入结果数组C中;不相同时,将A或B的三个元素直接存入结果数组中。
四、程序源代码
过程见后续,不想看过程的直接拉到底即可。
编写准备
首先,看一下稀疏矩阵的概念:
稀疏矩阵(Sparse Matrix):对于稀疏矩阵,目前还没有一个确切的定义。设矩阵A是一个n´m的矩阵中有s个非零元素,设 δ=s/(n´m),称δ为稀疏因子,如果某一矩阵的稀疏因子δ满足δ≦0.05时称为稀疏矩阵。
简单说就是一个有大量元素为ling3的数组。
以及矩阵相加:
一般是指在两个相同大小的矩阵,把其相对应元素加在一起的运算。
然后审查题目。
再程序分析中的“当行列相同时,将第三个元素值相加的和以及行列号三个元素存入结果数组C中;不相同时,将A或B的三个元素直接存入结果数组中。”这句话是编写的中心思想。
设计过程
定义部分
简单介绍一下
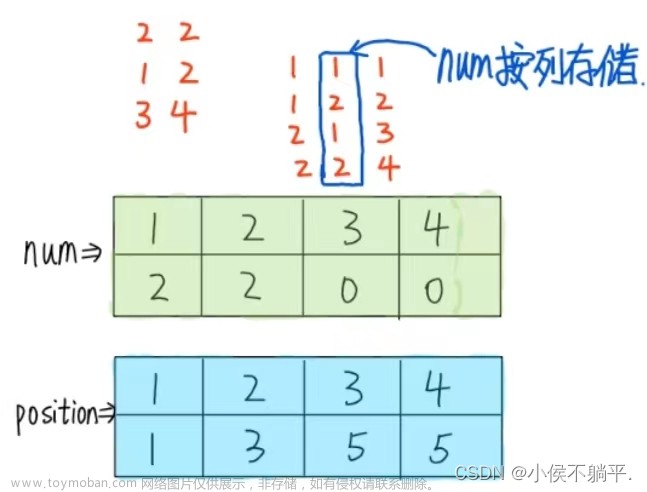
对于稀疏矩阵,采用压缩存储方法时,只存储非0元素。必须存储非0元素的行下标值、列下标值、元素值。因此,一个三元组(i, j, aij)唯一确定稀疏矩阵的一个非零元素。
三元组顺序表相应的数据结构定义如下:
//⑴ 三元组结点定义
#define MAX_SIZE 101
typedef struct
{
int row;//行下标
int col;//列下标
ElemType value;//元素值
}Triple;
//⑵ 三元组顺序表定义
typedef struct
{
int m;//行数
int n;//列数
int t;//非0元素个数
Triple data[MAX_SIZE];
}TMatrix;没有什么可更改的地方,直接拿来即可。
创建矩阵
直接上代码
void create_matrix(TMatrix &s,int M,int N)//矩阵创建
{
s.m=M;s.n=N;
printf("输入非0元素的个数:");
scanf("%d",&s.t);
for(int i=1;i<=s.t;i++)
{
printf("输入第%d个非0元素的行数、列数以及数值:",i);
scanf("%d%d%d",&s.data[i].row,&s.data[i].col,&s.data[i].value);
}
}M代表矩阵行数,N代表列数。
先输入非0元素的个数,然后依次输入非0元素即可。
矩阵显示
因为输入的是非零元素组成的矩阵,这里将其变换为普通的矩阵,方便观察现象。
void disp_matrix(TMatrix s)//矩阵显示
{
ElemType A[(s.m)+1][(s.n)+1]={0};//定义二维数组,并使初始值均为0
for(int temp=1;temp<=s.t;temp++)//非0元素进入数组
A[s.data[temp].row][s.data[temp].col]=s.data[temp].value;
for(int i=1;i<=s.m;i++)//显示完整的矩阵
{
for(int j=1;j<=s.n;j++)
printf(" %d",A[i][j]);
printf("\n");
}
}定义二维数组时(ElemType A[(s.m)+1][(s.n)+1]={0};)由于是从0开始计的,而创建函数是从1开始计的,为保持统一。
然后复刻非零元素即可。
最后输出。
矩阵相加函数
void add_matrix(TMatrix a,TMatrix b,TMatrix &c)//矩阵相加
{
int temp=1;
c.m=a.m;c.n=a.n;
c.t=0;
for(int i=1;i<=a.t;)
for(int j=1;j<=b.t;)
{
if(a.data[i].row>b.data[j].row)
{
c.data[temp].row=b.data[j].row;
c.data[temp].col=b.data[j].col;
c.data[temp].value=b.data[j].value;//小的给到c
c.t++;//非零元素加一
temp++;j++;
}
else if(a.data[i].row<b.data[j].row)
{
c.data[temp].row=a.data[i].row;
c.data[temp].col=a.data[i].col;
c.data[temp].value=a.data[i].value;//小的给到c
c.t++;//非零元素加一
temp++;i++;
}
else //行号相等
{
if(a.data[i].col>b.data[j].col)
{
c.data[temp].row=b.data[j].row;
c.data[temp].col=b.data[j].col;
c.data[temp].value=b.data[j].value;//小的给到c
c.t++;//非零元素加一
temp++;j++;
}
else if(a.data[i].col<b.data[j].col)
{
c.data[temp].row=a.data[i].row;
c.data[temp].col=a.data[i].col;
c.data[temp].value=a.data[i].value;//小的给到c
c.t++;//非零元素加一
temp++;i++;
}
else //列号也相等
{
c.data[temp].row=a.data[i].row;
c.data[temp].col=a.data[i].col;
c.data[temp].value=a.data[i].value+b.data[j].value;//加和并给到c
c.t++;//非零元素加一
temp++;i++;j++;
}
}
}
}拿出程序分析中的“当行列相同时,将第三个元素值相加的和以及行列号三个元素存入结果数组C中;不相同时,将A或B的三个元素直接存入结果数组中。”。要对比行列。
如果矩阵a和b同一位置上都有非零元素,则相加。
反之则直接给到c。
实现起来的话,先判断a和b的非零元素的行数,小的那个给到c,然后跳到下一元素。(如b的非零元素的行数小,则将b的非零元素的行、列和值给到c,然后跳到b的下一非零元素)。
然后再判断列数。
如若行数和列数都相等,将a的非零元素的值和b的相加,再给到c即可。
最后是主函数
int main()
{
TMatrix a,b,c;
int M,N;//m:行数 n:列数
printf("输入矩阵行数:");scanf("%d",&M);
printf("输入矩阵列数:");scanf("%d",&N);
printf("创建矩阵a:");create_matrix(a,M,N);
printf("完整的矩阵a:\n");disp_matrix(a);
printf("创建矩阵b:");create_matrix(b,M,N);
printf("完整的矩阵b:\n");disp_matrix(b);
add_matrix(a,b,c);
printf("非零元素矩阵c:非零元素共有%d个\n行下标 列下标 元素值\n",c.t);
for(int i=1;i<=c.t;i++)
printf(" %d %d %d\n",c.data[i].row,c.data[i].col,c.data[i].value);
printf("完整的矩阵c:\n");disp_matrix(c);
return 0;
}源代码:
#include<stdio.h>
#include<stdlib.h>
#define ElemType int
#define MAX_SIZE 101
typedef struct
{
int row;//行下标
int col;//列下标
ElemType value;//元素值
}Triple;
typedef struct
{
int m;//行数
int n;//列数
int t;//非0元素个数
Triple data[MAX_SIZE];
}TMatrix;
void create_matrix(TMatrix &s,int M,int N)//矩阵创建
{
s.m=M;s.n=N;
printf("输入非0元素的个数:");
scanf("%d",&s.t);
for(int i=1;i<=s.t;i++)
{
printf("输入第%d个非0元素的行数、列数以及数值:",i);
scanf("%d%d%d",&s.data[i].row,&s.data[i].col,&s.data[i].value);
}
}
void add_matrix(TMatrix a,TMatrix b,TMatrix &c)//矩阵相加
{
int temp=1;
c.m=a.m;c.n=a.n;
c.t=0;
for(int i=1;i<=a.t;)
for(int j=1;j<=b.t;)
{
if(a.data[i].row>b.data[j].row)
{
c.data[temp].row=b.data[j].row;
c.data[temp].col=b.data[j].col;
c.data[temp].value=b.data[j].value;//小的给到c
c.t++;//非零元素加一
temp++;j++;
}
else if(a.data[i].row<b.data[j].row)
{
c.data[temp].row=a.data[i].row;
c.data[temp].col=a.data[i].col;
c.data[temp].value=a.data[i].value;//小的给到c
c.t++;//非零元素加一
temp++;i++;
}
else //行号相等
{
if(a.data[i].col>b.data[j].col)
{
c.data[temp].row=b.data[j].row;
c.data[temp].col=b.data[j].col;
c.data[temp].value=b.data[j].value;//小的给到c
c.t++;//非零元素加一
temp++;j++;
}
else if(a.data[i].col<b.data[j].col)
{
c.data[temp].row=a.data[i].row;
c.data[temp].col=a.data[i].col;
c.data[temp].value=a.data[i].value;//小的给到c
c.t++;//非零元素加一
temp++;i++;
}
else //列号也相等
{
c.data[temp].row=a.data[i].row;
c.data[temp].col=a.data[i].col;
c.data[temp].value=a.data[i].value+b.data[j].value;//加和并给到c
c.t++;//非零元素加一
temp++;i++;j++;
}
}
}
}
void disp_matrix(TMatrix s)//矩阵显示
{
ElemType A[(s.m)+1][(s.n)+1]={0};//定义二维数组,并使初始值均为0
for(int temp=1;temp<=s.t;temp++)//非0元素进入数组
A[s.data[temp].row][s.data[temp].col]=s.data[temp].value;
for(int i=1;i<=s.m;i++)//显示完整的矩阵
{
for(int j=1;j<=s.n;j++)
printf(" %d",A[i][j]);
printf("\n");
}
}
int main()
{
TMatrix a,b,c;
int M,N;//m:行数 n:列数
printf("输入矩阵行数:");scanf("%d",&M);
printf("输入矩阵列数:");scanf("%d",&N);
printf("创建矩阵a:");create_matrix(a,M,N);
printf("完整的矩阵a:\n");disp_matrix(a);
printf("创建矩阵b:");create_matrix(b,M,N);
printf("完整的矩阵b:\n");disp_matrix(b);
add_matrix(a,b,c);
printf("非零元素矩阵c:非零元素共有%d个\n行下标 列下标 元素值\n",c.t);
for(int i=1;i<=c.t;i++)
printf(" %d %d %d\n",c.data[i].row,c.data[i].col,c.data[i].value);
printf("完整的矩阵c:\n");disp_matrix(c);
return 0;
}
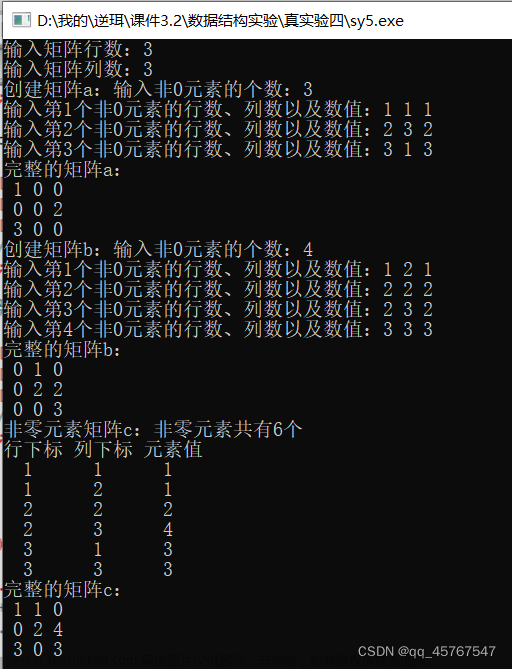
运行结果:文章来源:https://www.toymoban.com/news/detail-780247.html
 文章来源地址https://www.toymoban.com/news/detail-780247.html
文章来源地址https://www.toymoban.com/news/detail-780247.html
到了这里,关于稀疏矩阵的运算——矩阵相加的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!