PID控制参数整定（调节方法）原理+图示+MATLAB调试

Chapter1 PID控制参数整定（调节方法）原理+图示+MATLAB调试

原文链接：https://blog.csdn.net/viafcccy/article/details/107988093

序

首先最重要的是了解每个参数调节了系统响应的那些属性，通过观察响应从而调节参数改变属性。

PID的作用概述：
1、P产生响应速度和力度，过小响应慢，过大会产生振荡，是I和D的基础。
2、I在有系统误差和外力作用时消除偏差、提高精度，同时也会增加响应速度，产生过冲，过大会产生振荡。
3、D抑制过冲和振荡，过小系统会过冲，过大会减慢响应速度。D的另外一个作用是抵抗外界的突发干扰，阻止系统的突变。

同时调节的顺序是：P>I>D

下面了解的一个很重要的就是调节的目标，也就是最好的响应曲线是什么样子。

PID 调节目标：

1、衰减比在4-10之间最佳，也就是响应曲线的前两个峰值B:B1的比值在4-10之间。

2、稳态误差趋近于0

3、系统响应越快越好

一、P参数选取

tip：在第一步牢记P产生响应速度和力度，过小响应慢，过大会产生振荡，是I和D的基础。

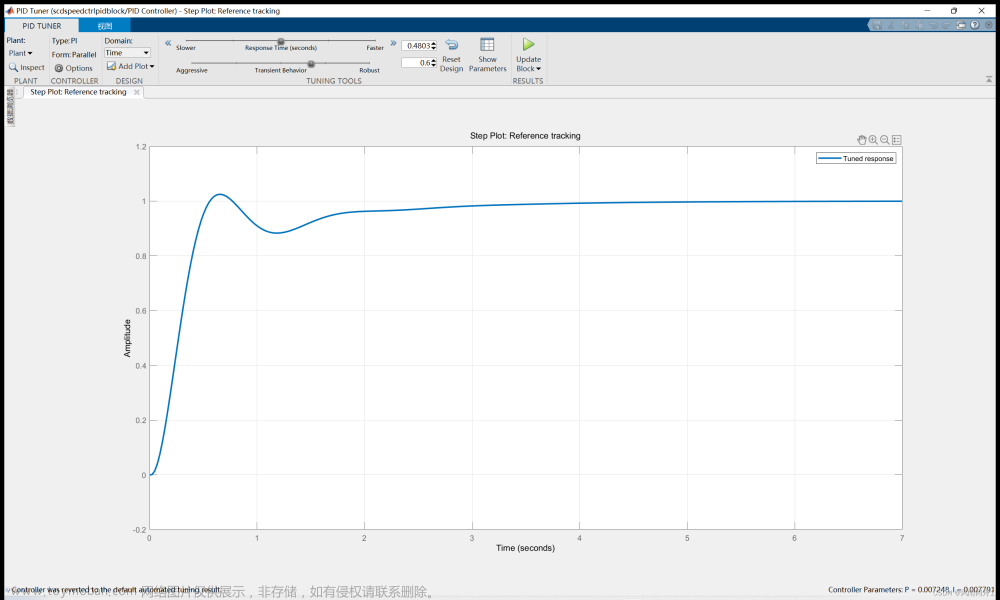
如果想自己调试尝试可以打开matlab，运行simulink，照着下面的图进行连接，如果想直接应用可以直接往后看。

图中的系统为一个PID控制二阶系统。

拿上面的系统进行举例，首先设定P=0.1，I=0，D=0观察响应。可以看到图像没有超调，说明P产生的响应速度和力度太小了，

P=1，I=0，D=0观察系统响应，超调量出现但是只有一个波形，同时也就意味着调节时间太慢了，继续加大P

P=10，I=0，D=0，此时调节时间显著下降，可以看到此时的数量级已经调整完成，也就是P参数只需要微调

P=100，I=0，D=0，系统开始变得振荡

如果继续加大P，系统会达到一个临界值，产生等幅振荡，最后开始发散。如下图所示：

二、I的调节

tip：I在有系统误差和外力作用时消除偏差、提高精度，同时也会增加响应速度，产生过冲，过大会产生振荡。

I主要调节稳态输出，消除扰动。由于系统没有扰动输入因此看不到I对于消除扰动的效果。P=10,I=10,D=0,此时I过大导致系统振荡加剧。

P=10,I=1,D=0，此时响应波形基本符合预期。观察稳态输出约为0.963左右。


P=10,I=0.1,D=0，可以看到几乎响应波形没有变化。说明在没有扰动的情况下I只要不过大影响不大。但是稳态输出变化为0.916


P=10,I=0,D=0,稳态输出变为0.91左右。

最终我们可以通过I少量调节稳态输出的值，最终将稳态误差消除。关于I对波形影响的作用总结如下图：

三、D的调节

tip:D抑制过冲和振荡，过小系统会过冲，过大会减慢响应速度。D的另外一个作用是抵抗外界的突发干扰，阻止系统的突变。

P=10，I=0.1，D=10，可以看到将所有的冲击都消除掉了。

P=10，I=0.1，D=1，消除冲击减弱，此时显然衰减比不符合要求

P=10，I=0.1，D=1，此时基本符合要求。

四、总结

首先调节P的数量级达到一个只有2个左右明显峰值的波形，再调节I找到不会波形振荡也不会没有超调的的区间，在区间内找到一个I将稳态误差尽可能消除。最终使用D来控制衰减比和波形的峰值、超调量。最后根据要求的稳态值、调节时间、超调量、上升时间、峰值时间等指标进行微调达到目标。

最后可以总结成一个口诀

参数整定找最佳，从小到大顺序查，
先是比例后积分，最后再把微分加，
曲线振荡很频繁，比例度盘要放大，
曲线漂浮绕大湾，比例度盘往小扳，
曲线偏离回复慢，积分时间往下降，
曲线波动周期长，积分时间再加长，
曲线振荡频率快，先把微分降下来，
动差大来波动慢，微分时间应加长，
理想曲线两个波，前高后低4比1，
一看二调多分析，调节质量不会低 。

Chapter2 PID参数调整，个人经验（配输出曲线图）

原文链接：https://blog.csdn.net/weixin_44407238/article/details/119255699

Chapter3 PID温度控制参数整定方法

原文链接：https://blog.csdn.net/pengzhihui2012/article/details/50380780

最近做了一个温度控制相关的项目，在此记录一下，方便以后查找，同时也供大家参考，欢迎指正，所有数据均为实验数据，绝对真实。

1.  位置式PID控制公式原型：u(t) = kp * e(t) + ki * [e(1) + e(2) + ....+ e(t)] + kd * [e(t) - e(t-1)]
   

2.  控制对象：加热/制冷器（在2分钟内不能再加热至冷之间切换）控制密封的腔体（空间体积大小15cm*20cm*65cm）温度。
   

3.  控制原理：利用MCU的输出比较模块（OCM）产生PWM波驱动H桥电路（通过目标温度和环境温度对比决定加热或者制冷）。
   

4.  PID参数整定
   

参数说明：

Kc： 只采用比例环节控制条件下，控制系统的稳态误差尽量达到最小时的Kp值。

Pc： 只采用比例环节控制条件下，控制系统的震荡周期。

Ti： 控制系统的积分时间。

Td： 控制系统的微分时间。

T： PID控制采样计算周期。

Kp、Ki、Kd：被整定的参数。

1）：获取合适的Kc值，设置Ki，Kd为0。在当前温度进入目标温度3.5°内开始进行PID控制，之前采用90%恒定功率加热。

图一（Kc =5）

图二（Kc =9）

图三（Kc =20）

从上述的四组数据中可以看到，当Kc=5时，控制系统的稳态误差是最小的。在目标范围正负3°之间，选取Kc = 5.

2）：计算Pc值。从上述的图一（将.csv格式的数据文件在excel中转换图表，将鼠标放在曲线上，会自动显示此点的坐标，如图所示），取4个震荡周期一共720个点，得出一个震荡周期为Pc=720*5/4= 900s。

3）：根据个人需要采用哪种PID组合来计算Ti、Td、Kp、Ki、Kd。温度控制是属于滞后控制，而PID控制中的，微分项是具有超前调节的作用，因此必须引入；积分项对误差的作用取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，推动控制器的输出向稳态误差减小的方向变化，直到稳态误差等于零。我采用的是PID组合来控制。得出Ti=9000.5=450s。Td=9000.15=135s。

Kp=50.65=3.25；Ki= KpT/Ti=3.255/450=0.036；Kd= KpTd/T=3.25*135s /5=88。

4）：采用PID控制温度，无论高温低温，稳态误差均在正负0.5°范围之内。如下所示：



一般根据模型计算的参数不一定是适合所有的控制系统（这里实验得到的最佳Kd值为120，而我们算出来的是88），根据特定的环境调节参数范围，找到最优参数，因本系统是滞后系统，微分项起主导作用，我暂时还只做了调整kd值的实验，Ki一般反应在系统达到稳态的时候是否存在稳定误差，从实验结果得出，稳态误差几乎可以忽略。

零下一度的目标温度，连续8小时的温度控制数据：

附录：//PWM频率为1Khz，定时器的计数周期为5000（mPID.MaxDuty = 5000*90%）,PID返回值和上次的的定时器技术值决定本次的占空比。

INT32 PID_calculate(double CurTemp)

{

    INT32 RetValue;

    doubleresult_value;

 

    // Keep previouserror

    mPID.PrevError =mPID.Error;

 

    // calculatecurrent error

    mPID.Error =mPID.Target - CurTemp;

 

    // calculateintegral

    mPID.SumError +=mPID.Error;

 

    if(mPID.Kd >0.0001)

    {

        result_value =mPID.Kp * mPID.Error + mPID.SumError * mPID.Ki +

                mPID.Kd* (mPID.Error - mPID.PrevError);

    }

    else

    {

        result_value =mPID.Kp * mPID.Error + mPID.SumError * mPID.Ki;

    }

    RetValue =(INT32)result_value;

    return RetValue;

}

//Timer interrupt enable control flag, execute temperaturecontrol.

//

void TemperatureControl()

{

    INT32 ret = 0;

    if(mPID.type ==HEAT)

    {

        INT32 DutyValue= OC4RS;

        if(fabs(mPID.Current- mPID.Target) <= PIDControlStartPoint)

        {

           PIDControlStartPoint = 12;

            ret =PID_calculate(mPID.Current);

        }

        elseif(fabs(mPID.Current - mPID.Target) <= TempControlStartPoint)

        {

            OC4RS = INITPWMPERIOD16 * 50 / 100.0;

            ret = 0;

            return ;

        }

        else

        {

            ret = 0;

        }

       

        if( (DutyValue+ ret) > mPID.MaxDuty)

            OC4RS =mPID.MaxDuty;

        else if(DutyValue+ ret < mPID.MinDuty)

            OC4RS =mPID.MinDuty;

        else

           OC4RS +=ret;

    }

    else if(mPID.type== COOL)

    {

        INT32 DutyValue= OC3RS;

       if(fabs(mPID.Current - mPID.Target) <= PIDControlStartPoint)

        {

           PIDControlStartPoint = 12;

            ret =PID_calculate(mPID.Current);

            ret = -ret;// must be negative

        }

        elseif(fabs(mPID.Current - mPID.Target) <= TempControlStartPoint)

        {

           if(mPID.Target > 5.1)

               OC3RS =INITPWMPERIOD16 * 70 / 100.0;

            else

               OC3RS =INITPWMPERIOD16 * 78 / 100.0;

           

            ret = 0;

            return ;

        }

        else

        {

            ret = 0;

        }

       

        if( (DutyValue+ ret) > mPID.MaxDuty)

            OC3RS =mPID.MaxDuty;

        elseif(DutyValue + ret < mPID.MinDuty)

            OC3RS =mPID.MinDuty;

        else

           OC3RS +=ret;

    }

    else

    {}

}

Chapter4 simulink中的PID模块的使用

原文链接：https://blog.csdn.net/wanrenqi/article/details/105278918

1、Simulink中PID模块的介绍

首先，找到PID模块，双击打开模块的参数设置，如下：

下面介绍几种常用功能的参数设置。

1.1、控制器类型选择

可以看到Controller：可以选择PI、PD和PID控制等。

1.2、PID控制器格式

Form：有并行（默认）和理想型（串行），其传函如下：

注意：传函中的P、I、D系数就是我们需要整定的三个PID参数。

1.3、时域选择

Time domain：连续时间和离散时间。
当选择离散时间时，需要设置积分器和微分器中的滤波器的离散化方法，有向前欧拉，后向欧拉，
双线性变换法，如下图：

1.4、PID的饱和输出限制

限制PID的输出，还有去饱和积分的方法，如，反算法、钳位法。如图所示：

当然我们也可以自己搭一个PID控制器。

2 、自建PID模块

下面搭建一个常用的离散型带输出饱和限制和积分饱和限制的PI控制器。如下：

从这个离散的PI控制模块中，可以看出积分环节是带有限幅输出的，当然还要对这个积分模块的限幅进行设置勾选，如图：

为什么我们需要对积分环节进行单独的限制输出。看个例子：

这个是带有积分饱和限制的PI控制器调节出来的系统响应。

这个是用simulink系统自带的PI控制器调节出来的系统响应，两个PI控制器的参数设置一样。但是带抗饱和积分的PI控制器调节出来的系统响应效果明显更好。

那么什么时候需要加积分环节限制输出呢？当系统在抗扰动时，需要一个大的Ki参数来快速消除稳态误差，而在开始从0到稳态这个过程又会因为ki太大而引起过大超调时，这个时候就需要加积分过饱和限制。

Chapter5 simulink实现模糊PID控制

原文链接：https://blog.csdn.net/qq_36949278/article/details/105569943

模糊系统建立

在matlab命令行输入fuzzy打开模糊系统设计器，设定输入个数为2，范围均为[-3,3]，输出个数为3，范围均为[-1,1]，模糊系统如下图。根据相关文献定义规则，将建立好的模糊文件命名为Fuzzy_PID并保存到本地文件中，用于下一步的导入。

simulink实现

主程序设计
通过阶跃函数模拟输入信号，将输入信号分别传入自带PID模块与编写的模糊PID模块，将两个模块的控制结果及阶跃信号值通过scope函数进行展示，整体程序框图如下。

PID模块参数设置为P：0.05，I：0.01，D：0.005。

模糊PID模块

将阶跃信号传入系统，系统通过反馈计算误差及误差变化率，将误差及误差变化率乘以各自的量化因子，模糊系统的误差及误差变化率的值域均为[-3,3]，假设实际的误差范围为[-8,8]，误差变化率范围为[-16,16]，则量化因子分别为0.375和0.1875。量化后的值通过saturation函数处理后传入模糊系统，模糊系统设定如下图，其中Fuzzy_PID应在命令行通过如下语句导入到系统中。

Fuzzy_PID = readfis(‘Fuzzy_PID’)

模糊系统设定输出的范围均为[-1,1]，因此也应根据相关经验乘以量化因子，并与初始PID参数，即P：0.05，I：0.01，D：0.005求和，处理后的参数传入PID系统中，结合了模糊规则及PID控制的系统即为模糊PID控制系统，系统的程序框图如下。

结果展示

运行程序，点击scope可查看运行结果如下图，可以看出模糊PID比单独PID更早到达设定值，具有更好的响应速度。

Chapter6 飞思卡尔智能车----模糊PID算法通俗讲

在讲解模糊PID前，我们先要了解PID控制器的原理（本文主要介绍模糊PID的运用,对PID控制器的原理不做详细介绍）。PID控制器（比例-积分-微分控制器）是一个在工业控制应用中常见的反馈回路部件，由比例单元P、积分单元I和微分单元D组成。PID控制的基础是比例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快大惯性系统响应速度以及减弱超调趋势。

1.1传统PID控制

传统PID控制器自出现以来，凭借其结构简单、稳定性好、工作可靠、调整方便等优点成为工业控制主要技术。当被控对象的结构和参数具有一定的不确定性，无法对其建立精确的模型时，采用PID控制技术尤为方便。PID控制原理简单、易于实现，但是其参数整定异常麻烦。对于小车的速度控制系统而言，由于其为时变非线性系统不同时刻需要选用不同的PID参数，采用传统的PID控制器，很难使整个运行过程具有较好的运行效果。

1.2模糊PID控制

模糊PID控制，即利用模糊逻辑并根据一定的模糊规则对PID的参数进行实时的优化，以克服传统PID参数无法实时调整PID参数的缺点。模糊PID控制包括模糊化，确定模糊规则，解模糊等组成部分。小车通过传感器采集赛道信息，确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec，根据给定的模糊规则进行模糊推理，最后对模糊参数进行解模糊，输出PID控制参数。

2.1模糊化

模糊控制器主要由三个模块组成：模糊化，模糊推理，清晰化。具体如下图所示。而我们将一步步讲解如何将模糊PID算法运用到智能车上。（最好用笔一步步自己写一遍！！！）

首先我们的智能车会采集到赛道的相关数据，例如摄像头车，其采集到的数据经过算法处理之后会得到与中线的偏差E，以及当前偏差和上次偏差的变化（差值）EC两个值（即此算法为2维输入，同理也可以是1维和3维，但2维更适合智能车）。例如此时车偏离中线的距离为150，而上一时刻偏离中线的距离为120，则E为150，EC为150 - 120 = 30。

其次我们要对这两个值进行模糊化。这里我们对E进行举例。摄像头车采集回来的E是有范围的，即与中线的偏差是在一个区间内可行的。在这里我们假设该区间为-240到240，即小车偏离中线的最大距离为240，正负即为左右。再假设中线偏差变化率的可行区间为-40到+40。

接着我们要对这两个值进行模糊化。我现在将E的区间（-240 到 240）分成8个部分，那么他们分别为-240 ~ -180，-180 ~ -120 ，-120 ~ -60，-60 ~ 0，0 ~ 60，60 ~ 120，120 ~ 180，180 ~ 240。然后我们把-180，-120，-60，0，60，120，180分别用NB，NM，NS，ZO，PS，PM，PB表示（个人理解N为negative，P为positive，B为big，M为middle，S为small，ZO为zero）。例如，当E = 170时，此时的E属于PM和PB之间，而此时的E也会对应2（或1）个隶属度。E隶属于PM（120）的百分比为（180 - 170） / （180 - 120） = 1 / 6 ，而同理隶属于PB（180）的百分比为（170 - 120） / （180 - 120） = 5 / 6 。意思就是120到180进行线性分割了，E离PM和PB哪个更近，则隶属于哪个就更大（当输出值E大于180（PB）时，则隶属度为1，隶属度值为PB，即E完全隶属于PB，同理当E小于 - 180 （NB）时也一样）。同理也可以对EC进行模糊化。

2.2 模糊推理

对于采集回来的E和EC，我们可以推出它们各所占的隶属度，此时我们可以根据模糊规则表去找出输出值所对应的隶属度。

我们假设为E的两个隶属度值为PM、PB,E属于PM的隶属度为a（a < 1），则属于PB的隶属度为（1 - a）。再假设EC的两个隶属度值为NB、NM，EC属于NM的隶属度为b，则属于NB的隶属度为（1 - b）。而在假设中，E属于PM的隶属度为a，EC属于NB的隶属度为( 1 - b )，则输出值属于ZO的隶属度为a *( 1 - b )（看图）。

同理我们可以得出，当输出值属于ZO的另外两个隶属度为a * b， （ 1 - a ） * （ 1 - b） ，而输出值属于NS的隶属度为（ 1 - a ） * 1 - b。

   在这里我们先证明一个条件，将这四个隶属度加起来，刚好等于1。这是因为

    （a + （1 - a）） * （b + （1 - b）） = a * b + ( 1 - a ) *  b  + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b )   （下图）

   即一个十字相乘的概念。这个等式说明输出值的隶属度之和等于1（第三步求解的时候需要用到隶属度之和）。

因此，我们知道了输出值为ZO的隶属度和为 a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ，输出值为NS的隶属度为 ( 1 - a ) * b 。

2.3 清晰化

对于输出值，我们同样采用给予隶属度的办法。例如，我们把输出值假设为[1000，1400]（即舵机的摆角值范围）的区间同样划分为八个部分，即7个隶属值NB,NM,NS,ZO,PS,PM,PB。根据上一步所得出的结论，我们就可以用隶属度乘以相应的隶属值算出输出值的解，即 （a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ） * ZO + ( 1 - a ) * b * NS。到此为止，整个模糊过程就结束了。

3 模糊PID

我们已经知道了整个模糊的过程，但上述的过程还不够完美。因为我们的输出值只有一个输出，并没有实现PID。因此我们可以先对E和EC进行模糊化，然后分别对kp和ki和kd（PID的三个参数）进行求解，再套入公式。

一般的我们也可以只用kp，kd，不用ki。而模糊规则表一般的论文已经基本给出。因此带入算法之后我们的难度也只是在于调节kp，kd，和适当调节规则表。当然调节的难度会大于普通的PID，因为还要定kp，kd的输出范围，调得不好可能效果并没有普通的PID好。

4. 部分解释

4.1对于部分论文所说的重心法解模糊，其实就是上述方法。公式如下。

式中μ（Zi） * Zi相当于文章上面的（a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ） * ZO + ( 1 - a ) * b * NS，即隶属度乘以隶属度值之和，而μ（Zi）之和就是输出值的隶属度之和，我们已经证明它是等于1的。

Chapter7 模糊自适应整定PID控制

原文链接

Chapter8 自适应模糊PID（位置式）C语言实现

原文链接：https://blog.csdn.net/qq_30759585/article/details/122382396

一、自适应模糊PID原理

自适应模糊PID 控制系统结构如图所示。控制系统以偏差e和偏差变化率ec作为输入量，利用模糊规则进行模糊推理，输出Δkp，Δki，Δkd。对PID三个参数进行在线分析与调整，而自适应模糊PID 控制器输出u( t) 作用Mosfet开关管上，从而使sepic的输出电压达到要求的实时稳定性。

图 4.2.1 模糊PID结构图
系统采用两输入一输出的模糊控制器的形式，以密度偏差e 和偏差变化率ec 作为模糊控制器的输入量，以PID 参数的修正量Δkp，Δki，Δkd分别为模糊控制器的输出量。其变量、基本论域、模糊子集、模糊论域、量化因子、比例因子如表所示。考虑到论域覆盖范围和灵敏度，并且为了F28027计算简便，各模糊子集采用三角形隶属函数。
表 4.2.1 ΔKp模糊规则表

表4.2.2ΔKi模糊规则表

表4.2.3ΔKd模糊规则表


图4.2.2 隶属度函数
根据已经确立的模糊控制规则和隶属度函数，采用Mamdani推理方法，面积重心法非模糊化。

总结一下，整个模糊自适应PID的运算工程如下所示：

二、代码实现

该工程来自https://github.com/FlameAlpha/fuzzy-pid
某位国内大佬编写，顶礼膜拜。文章来源地址https://www.toymoban.com/news/detail-780333.html

fuzzy_pid.h

#ifndef _FUZZY_PID_H_
#define _FUZZY_PID_H_

#ifdef __cplusplus
extern "C" {
#endif


#include "math.h"
#include "stdlib.h"
#include "User_Component/mySci/printf.h"



#ifndef bool
#define bool char
#endif

#ifndef false
#define false (char)0
#endif

#ifndef true
#define true (char)1
#endif


// Fuzzy quantity fields
enum quantity_fields
{
    qf_small = 5,
    qf_middle = 7,
    qf_large = 8
};

#define qf_default qf_middle

struct fuzzy
{
    unsigned int input_num;
    unsigned int output_num;
    unsigned int fo_type;
    unsigned int *mf_type;
    int *mf_params;
    unsigned int df_type;
    int *rule_base;
    float *output;
};

struct PID
{
    float kp;
    float ki;
    float kd;

    float delta_kp_max;
    float delta_ki_max;
    float delta_kd_max;

    float delta_kp;
    float delta_ki;
    float delta_kd;

    float error_max;
    float delta_error_max;

    float last_error;
    float current_error;

    float intergral;
    float intergral_limit;

    float dead_zone;
    float feed_forward;

    float output;

    int output_min_value;
    int output_middle_value;
    int output_max_value;

    float linear_adaptive_kp;

    struct fuzzy *fuzzy_struct;
};

#define NB -3
#define NM -2
#define NS -1
#define ZO 0
#define PS 1
#define PM 2
#define PB 3



//#define fuzzy_pid_debug_print
//#define fuzzy_pid_dead_zone
//#define fuzzy_pid_integral_limit
//#define fuzzy_pid_rule_base_deep_copy

#define pid_params_count 7

#define torque_mode 1
#define position_mode 2
#define control_mode position_mode

#if control_mode == position_mode
#define max_error 5.0f
#define max_delta_error 5.0f
#else
#define max_error 12.0f
#define max_delta_error 12.0f
#endif

#define min_pwm_output 250
#define middle_pwm_output 1500
#define max_pwm_output 2900

struct fuzzy *fuzzy_init(unsigned int input_num, unsigned int output_num);

void fuzzy_params_init(struct fuzzy *fuzzy_struct, unsigned int mf_type, unsigned int fo_type, unsigned int df_type,
                       int mf_params[], int rule_base[][qf_default]);

void fuzzy_control(float e, float de, struct fuzzy *fuzzy_struct);



struct PID *raw_fuzzy_pid_init(float kp, float ki, float kd, float integral_limit, float dead_zone,
                               float feed_forward, float error_max, float delta_error_max, float delta_kp_max,
                               float delta_ki_max, float delta_kd_max, unsigned int mf_type, unsigned int fo_type,
                               unsigned int df_type, int *mf_params, int rule_base[][qf_default],
                               int output_min_value, int output_middle_value, int output_max_value);

//float params[pid_params_count] = {kp, ki, kd, integral_limit, dead_zonefeed_forward, linear_adaptive_kp};


struct PID *fuzzy_pid_init(float *params, float delta_k, unsigned int mf_type, unsigned int fo_type,
                           unsigned int df_type, int mf_params[], int rule_base[][qf_default]);


struct PID **
fuzzy_pid_vector_init(float params[][pid_params_count], float delta_k, unsigned int mf_type, unsigned int fo_type,
                      unsigned int df_type, int *mf_params, int rule_base[][qf_default],
                      unsigned int count);


float fuzzy_pid_control(float real, float idea, struct PID *pid);

int direct_control(int zero_value, int offset_value, bool direct);


int fuzzy_pid_motor_pwd_output(float real, float idea, bool direct, struct PID *pid);

void delete_pid(struct PID *pid);

void delete_pid_vector(struct PID **pid_vector, unsigned int count);

#ifdef __cplusplus
}
#endif

#endif //_FUZZY_PID_H_

fuzzy_pid.c

#include "User_Component/myPID/fuzzy_pid.h"

struct fuzzy *fuzzy_init(unsigned int input_num, unsigned int output_num)
{
    struct fuzzy *fuzzy_struct = (struct fuzzy *) malloc(sizeof(struct fuzzy));
    fuzzy_struct->input_num = input_num;
    fuzzy_struct->output_num = output_num;
    fuzzy_struct->mf_type = (unsigned int *) malloc((input_num + output_num) * sizeof(unsigned int));
#ifdef fuzzy_pid_rule_base_deep_copy
    fuzzy_struct->mf_params = (int *) malloc(4 * qf_default * sizeof(int));
    fuzzy_struct->rule_base = (int *) malloc(output_num * qf_default * qf_default * sizeof(int));
#endif
    fuzzy_struct->output = (float *) malloc(output_num * sizeof(float));
    return fuzzy_struct;
}

void delete_fuzzy(struct fuzzy *fuzzy_struct)
{
    free(fuzzy_struct->mf_type);
    free(fuzzy_struct->output);
    free(fuzzy_struct);
}

void fuzzy_params_init(struct fuzzy *fuzzy_struct, unsigned int mf_type, unsigned int fo_type, unsigned int df_type,
                       int mf_params[], int rule_base[][qf_default])
{
    for (unsigned int i = 0; i < fuzzy_struct->input_num + fuzzy_struct->output_num; ++i)
    {
        fuzzy_struct->mf_type[i] = mf_type;
    }

    for (unsigned int i = 0; i < fuzzy_struct->output_num; ++i)
    {
        fuzzy_struct->output[i] = 0;
    }

#ifdef fuzzy_pid_rule_base_deep_copy
    for (unsigned int j = 0; j < 4 * qf_default; ++j)
    {
        fuzzy_struct->mf_params[j] = mf_params[j];
    }

    for (unsigned int k = 0; k < fuzzy_struct->output_num * qf_default; ++k)
    {
        for (unsigned int i = 0; i < qf_default; ++i)
        {
            fuzzy_struct->rule_base[k * 7 + i] = rule_base[k][i];
        }
    }
#else
    fuzzy_struct->mf_params = mf_params;
    fuzzy_struct->rule_base = (int *) rule_base;
#endif

    fuzzy_struct->fo_type = fo_type;
    fuzzy_struct->df_type = df_type;
}

#define inverse(parameter) 1.0f/(float)parameter

// Gaussian membership function
float gaussmf(float x, float sigma, float c)
{
    return expf(-powf(((x - c) / sigma), 2.0f));
}

// Generalized bell-shaped membership function
float gbellmf(float x, float a, float b, float c)
{
    return inverse(1.0f + powf(fabsf((x - c) / a), 2.0f * b));
}

// Sigmoidal membership function
float sigmf(float x, float a, float c)
{
    return inverse(1.0f + expf(a * (c - x)));
}

// Trapezoidal membership function
float trapmf(float x, float a, float b, float c, float d)
{
    if (x >= a && x < b)
        return (x - a) / (b - a);
    else if (x >= b && x < c)
        return 1.0f;
    else if (x >= c && x <= d)
        return (d - x) / (d - c);
    else return 0.0f;
}

// Triangular membership function
float trimf(float x, float a, float b, float c)
{
    return trapmf(x, a, b, b, c);
}

// Z-shaped membership function
float zmf(float x, float a, float b)
{
    if (x <= a)
        return 1.0f;
    else if (x >= a && x <= (a + b) / 2.0f)
        return 1.0f - 2.0f * powf((x - a) / (b - a), 2.0f);
    else if (x >= (a + b) / 2.0f && x < b)
        return 2.0f * powf((x - b) / (b - a), 2.0f);
    else return 0;
}

// Membership function
float mf(float x, unsigned int mf_type, int *params)
{
    switch (mf_type)
    {
    case 0:
        return gaussmf(x, params[0], params[1]);
    case 1:
        return gbellmf(x, params[0], params[1], params[2]);
    case 2:
        return sigmf(x, params[0], params[2]);
    case 3:
        return trapmf(x, params[0], params[1], params[2], params[3]);
    case 5:
        return zmf(x, params[0], params[1]);
    default: // set triangular as default membership function
        return trimf(x, params[0], params[1], params[2]);
    }
}

// Union operator
float or (float a, float b, unsigned int type)
{
    if (type == 1)   // algebraic sum
    {
        return a + b - a * b;
    }
    else if (type == 2)     // bounded sum
    {
        return fminf(1, a + b);
    }
    else     // fuzzy union
    {
        return fmaxf(a, b);
    }
}

// Intersection operator
float and (float a, float b, unsigned int type)
{
    if (type == 1)   // algebraic product
    {
        return a * b;
    }
    else if (type == 2)     // bounded product
    {
        return fmaxf(0, a + b - 1);
    }
    else     // fuzzy intersection
    {
        return fminf(a, b);
    }
}

// Equilibrium operator
float equilibrium(float a, float b, float params)
{
    return powf(a * b, 1 - params) * powf(1 - (1 - a) * (1 - b), params);
}

// Fuzzy operator
float fo(float a, float b, unsigned int type)
{
    if (type < 3)
    {
        return and (a, b, type);
    }
    else if (type < 6)
    {
        return or (a, b, type - 3);
    }
    else
    {
        return equilibrium(a, b, 0.5f);
    }
}

// Mean of centers defuzzifier, only for two input multiple index
void moc(const float *joint_membership, const unsigned int *index, const unsigned int *count, struct fuzzy *fuzzy_struct)
{

    float denominator_count = 0;
//    float numerator_count[fuzzy_struct->output_num];
    //注意 TI的C99编译器并不是完全支持动态数组的特性，所以这里改变了一下（c89写法）
    float *numerator_count= (float *)malloc(fuzzy_struct->output_num*sizeof(float));

    for (unsigned int l = 0; l < fuzzy_struct->output_num; ++l)
    {
        numerator_count[l] = 0;
    }

    for (int i = 0; i < count[0]; ++i)
    {
        for (int j = 0; j < count[1]; ++j)
        {
            denominator_count += joint_membership[i * count[1] + j];
        }
    }

    for (unsigned int k = 0; k < fuzzy_struct->output_num; ++k)
    {
        for (unsigned int i = 0; i < count[0]; ++i)
        {
            for (unsigned int j = 0; j < count[1]; ++j)
            {
                numerator_count[k] += joint_membership[i * count[1] + j] *
                                      fuzzy_struct->rule_base[k * qf_default * qf_default + index[i] * qf_default +
                                                index[count[0] + j]];
            }
        }
    }

#ifdef fuzzy_pid_debug_print
    printf("output:\n");
#endif
    for (unsigned int l = 0; l < fuzzy_struct->output_num; ++l)
    {
        fuzzy_struct->output[l] = numerator_count[l] / denominator_count;
#ifdef fuzzy_pid_debug_print
        printf("%f,%f,%f\n", numerator_count[l], denominator_count, fuzzy_struct->index[l]);
#endif
    }
    free(numerator_count);//有借有还再借不难
}

// Defuzzifier
void df(const float *joint_membership, const unsigned int *output, const unsigned int *count, struct fuzzy *fuzzy_struct,
        int df_type)
{
    if (df_type == 0)
        moc(joint_membership, output, count, fuzzy_struct);
    else
    {
        printf("Waring: No such of defuzzifier!\n");
        moc(joint_membership, output, count, fuzzy_struct);
    }
}

void fuzzy_control(float e, float de, struct fuzzy *fuzzy_struct)
{
    float membership[qf_default * 2]; // Store membership
    unsigned int index[qf_default * 2]; // Store the index of each membership
    unsigned int count[2] = {0, 0};

    {
        int j = 0;
        for (int i = 0; i < qf_default; ++i)
        {
            float temp = mf(e, fuzzy_struct->mf_type[0], fuzzy_struct->mf_params + 4 * i);
//            if (temp > 1e-4)
//            {
                membership[j] = temp;
                index[j++] = i;
//            }
        }

        count[0] = j;

        for (int i = 0; i < qf_default; ++i)
        {
            float temp = mf(de, fuzzy_struct->mf_type[1], fuzzy_struct->mf_params + 4 * i);
//            if (temp > 1e-4)
//            {
                membership[j] = temp;
                index[j++] = i;
//            }
        }

        count[1] = j - count[0];
    }

#ifdef fuzzy_pid_debug_print
    printf("membership:\n");
    for (unsigned int k = 0; k < j; ++k)
    {
        printf("%f\n", membership[k]);
    }

    printf("index:\n");
    for (unsigned int k = 0; k < j; ++k)
    {
        printf("%d\n", index[k]);
    }

    printf("count:\n");
    for (unsigned int k = 0; k < 2; ++k)
    {
        printf("%d\n", count[k]);
    }
#endif

    if (count[0] == 0 || count[1] == 0)
    {
        for (unsigned int l = 0; l < fuzzy_struct->output_num; ++l)
        {
            fuzzy_struct->output[l] = 0;
        }
        return;
    }

    // Joint membership
//注意 TI的C99编译器并不是完全支持动态数组的特性，所以这里改变了一下（c89写法）
//    float joint_membership[count[0] * count[1]];
    float *joint_membership= (float *)malloc(count[0] * count[1]*sizeof(float));

    for (int i = 0; i < count[0]; ++i)
    {
        for (int j = 0; j < count[1]; ++j)
        {
            joint_membership[i * count[1] + j] = fo(membership[i], membership[count[0] + j], fuzzy_struct->fo_type);
        }
    }

    df(joint_membership, index, count, fuzzy_struct, 0);

    free(joint_membership);
}

struct PID *raw_fuzzy_pid_init(float kp, float ki, float kd, float integral_limit, float dead_zone,
                               float feed_forward, float error_max, float delta_error_max, float delta_kp_max,
                               float delta_ki_max, float delta_kd_max, unsigned int mf_type, unsigned int fo_type,
                               unsigned int df_type, int mf_params[], int rule_base[][qf_default],
                               int output_min_value, int output_middle_value, int output_max_value)
{
    struct PID *pid = (struct PID *) malloc(sizeof(struct PID));
    pid->kp = kp;
    pid->ki = ki;
    pid->kd = kd;

    pid->delta_kp_max = delta_kp_max;
    pid->delta_ki_max = delta_ki_max;
    pid->delta_kd_max = delta_kd_max;

    pid->delta_kp = 0;
    pid->delta_ki = 0;
    pid->delta_kd = 0;

    pid->error_max = error_max;
    pid->delta_error_max = delta_error_max;

    int output_count = 1;
    if (ki > 1e-4)
    {
        output_count += 1;
        if (kd > 1e-4)
            output_count += 1;
    }

    pid->fuzzy_struct = fuzzy_init(2, output_count);
    fuzzy_params_init(pid->fuzzy_struct, mf_type, fo_type, df_type, mf_params, rule_base);

    pid->last_error = 0;
    pid->current_error = 0;

    pid->intergral = 0;
    pid->intergral_limit = integral_limit;

    pid->dead_zone = dead_zone;
    pid->feed_forward = feed_forward;

    pid->output_max_value = output_max_value;
    pid->output_middle_value = output_middle_value;
    pid->output_min_value = output_min_value;

    return pid;
}

struct PID *fuzzy_pid_init(float *params, float delta_k, unsigned int mf_type, unsigned int fo_type,
                           unsigned int df_type, int mf_params[], int rule_base[][qf_default])
{
    return raw_fuzzy_pid_init(params[0], params[1], params[2], params[3], params[4], params[5], max_error,
                              max_delta_error, params[0] / delta_k, params[1] / delta_k, params[2] / delta_k, mf_type,
                              fo_type, df_type, mf_params,
                              rule_base, min_pwm_output, middle_pwm_output, max_pwm_output);
}


int round_user(float parameter)
{
    if ((int)(parameter * 10.0) % 10 >= 5)
        return parameter + 1;
    else
        return parameter;
}

int limit(int value, int max_limit, int min_limit)
{
    if (value > max_limit)
        return max_limit;
    if (value < min_limit)
        return min_limit;
    return value;
}
float limits(float value, float max_limit, float min_limit)
{
    if (value > max_limit)
        return max_limit;
    if (value < min_limit)
        return min_limit;
    return value;
}

float fuzzy_pid_control(float real, float idea, struct PID *pid)
{
    pid->last_error = pid->current_error;
    pid->current_error = idea - real;
    float delta_error = pid->current_error - pid->last_error;
    float uk;
#ifdef fuzzy_pid_dead_zone
    if (pid->current_error < pid->dead_zone && pid->current_error > -pid->dead_zone)
    {
        pid->current_error = 0;
    }
    else
    {
        if (pid->current_error > pid->dead_zone)
            pid->current_error = pid->current_error - pid->dead_zone;
        else
        {
            if (pid->current_error < -pid->dead_zone)
                pid->current_error = pid->current_error + pid->dead_zone;
        }
    }
#endif

    //关键代码
    fuzzy_control(pid->current_error / pid->error_max * 3.0f, delta_error / pid->delta_error_max * 3.0f,
                  pid->fuzzy_struct);

//    pid->delta_kp = limits(pid->fuzzy_struct->output[0]/3.0f * pid->delta_kp_max, pid->delta_kp_max ,-pid->delta_kp_max);
    pid->delta_kp = limits(pid->fuzzy_struct->output[0], pid->delta_kp_max ,-pid->delta_kp_max);

    if (pid->fuzzy_struct->output_num >= 2)

//        pid->delta_ki = limits(pid->fuzzy_struct->output[1]/3.0f * pid->delta_ki_max, pid->delta_ki_max ,-pid->delta_ki_max);
        pid->delta_ki = limits(pid->fuzzy_struct->output[1], pid->delta_ki_max ,-pid->delta_ki_max);
    else pid->delta_ki = 0;

    if (pid->fuzzy_struct->output_num >= 3)

//        pid->delta_kd =limits(pid->fuzzy_struct->output[2]/3.0f * pid->delta_kd_max, pid->delta_kd_max ,-pid->delta_kd_max);
        pid->delta_kd =limits(pid->fuzzy_struct->output[2], pid->delta_kd_max ,-pid->delta_kd_max);

    else pid->delta_kd = 0;

#ifdef fuzzy_pid_debug_print
    printf("kp : %f, ki : %f, kd : %f\n", pid->kp + pid->delta_kp, pid->ki + pid->delta_ki, pid->kd + pid->delta_kd);
#endif

//    printf("kpkikd:%f,%f,%f,%f\n", pid->kp + pid->delta_kp, pid->ki + pid->delta_ki, pid->kd + pid->delta_kd,0.0);

    pid->intergral += (pid->ki + pid->delta_ki) * pid->current_error;
#ifdef fuzzy_pid_integral_limit
    if (pid->intergral > pid->intergral_limit)
        pid->intergral = pid->intergral_limit;
    else
    {
        if (pid->intergral < -pid->intergral_limit)
            pid->intergral = -pid->intergral_limit;
    }
#endif
    // //这里位置式PID算法

//    pid->output = (pid->kp + pid->delta_kp) * pid->current_error + pid->intergral +
//                  (pid->kd + pid->delta_kd) * (pid->current_error - pid->last_error);

    uk = (pid->kp + pid->delta_kp) * pid->current_error + pid->intergral +
                  (pid->kd + pid->delta_kd) * (pid->current_error - pid->last_error);

//    pid->output += pid->feed_forward * (float) idea;

    uk +=pid->feed_forward * (float) idea;//前馈环节

    pid->output = uk;

    //限幅
    if(pid->output<pid ->output_min_value)
        pid->output=pid ->output_min_value;
    else if (pid->output>pid ->output_max_value)
        pid->output=pid ->output_max_value;

    return pid->output;
}


void delete_pid(struct PID *pid)
{
    if (pid->fuzzy_struct != NULL)
    {
        delete_fuzzy(pid->fuzzy_struct);
    }
    free(pid);
}

void delete_pid_vector(struct PID **pid_vector, unsigned int count)
{
    for (unsigned int i = 0; i < count; ++i)
    {
        delete_pid(pid_vector[i]);
    }
    free(pid_vector);
}



struct PID **
fuzzy_pid_vector_init(float params[][pid_params_count], float delta_k, unsigned int mf_type, unsigned int fo_type,
                      unsigned int df_type, int *mf_params, int rule_base[][qf_default],
                      unsigned int count)
{
    struct PID **pid = (struct PID **) malloc(sizeof(struct PID *) * count);
    for (unsigned int i = 0; i < count; ++i)
    {
        pid[i] = fuzzy_pid_init(params[i], delta_k, mf_type, fo_type, df_type, mf_params, rule_base);
    }
    return pid;
}

int direct_control(int zero_value, int offset_value, bool direct)
{
    if (direct == true)
    {
        return zero_value + offset_value;
    }
    else
    {
        return zero_value - offset_value;
    }
}

int fuzzy_pid_motor_pwd_output(float real, float idea, bool direct, struct PID *pid)
{
    return limit(direct_control(pid->output_middle_value, fuzzy_pid_control(real, idea, pid), direct),
                 pid->output_max_value, pid->output_min_value);
}

调用方法

//全局变量定义方式
struct PID **pid_vector;

//main函数中初始化

     int rule_base[][qf_default] = {
            //delta kp rule base
            {PB, PB, PM, PM, PS, ZO, ZO},
            {PB, PB, PM, PS, PS, ZO, NS},
            {PM, PM, PM, PS, ZO, NS, NS},
            {PM, PM, PS, ZO, NS, NM, NM},
            {PS, PS, ZO, NS, NS, NM, NM},
            {PS, ZO, NS, NM, NM, NM, NB},
            {ZO, ZO, NM, NM, NM, NB, NB},
            //delta ki rule base
            {NB, NB, NM, NM, NS, ZO, ZO},
            {NB, NB, NM, NS, NS, ZO, ZO},
            {NB, NM, NS, NS, ZO, PS, PS},
            {NM, NM, NS, ZO, PS, PM, PM},
            {NM, NS, ZO, PS, PS, PM, PB},
            {ZO, ZO, PS, PS, PM, PB, PB},
            {ZO, ZO, PS, PM, PM, PB, PB},
            //delta kd rule base
            {PS, NS, NB, NB, NB, NM, PS},
            {PS, NS, NB, NM, NM, NS, ZO},
            {ZO, NS, NM, NM, NS, NS, ZO},
            {ZO, NS, NS, NS, NS, NS, ZO},
            {ZO, ZO, ZO, ZO, ZO, ZO, ZO},
            {PB, PS, PS, PS, PS, PS, PB},
            {PB, PM, PM, PM, PS, PS, PB}};

     // Default parameters of membership function
     int mf_params[4 * qf_default] = {-3, -3, -2, 0,
                                     -3, -2, -1, 0,
                                     -2, -1,  0, 0,
                                     -1,  0,  1, 0,
                                      0,  1,  2, 0,
                                      1,  2,  3, 0,
                                      2,  3,  3, 0};

     float fuzzy_pid_params[1][pid_params_count] = {{25.4597502f,  10.0053997f,    15.59500027f,    1800, 0, 0, 1}};

     struct PID **subpid_vector = fuzzy_pid_vector_init(fuzzy_pid_params, 4.0f, 4, 1, 0, mf_params, rule_base, 1);

     pid_vector=subpid_vector;
     
//中断中调用
        control_uk = fuzzy_pid_control(Voltage_Real, pid.Ref, pid_vector[0]);
        if(control_uk<150)
            control_uk=150;
        else if (control_uk>2800)
            control_uk=2800;

到了这里，关于PID控制参数整定（调节方法）原理+图示+MATLAB调试的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！