3.4动态规划--最大字段和-Toy模板网

这篇具有很好参考价值的文章主要介绍了3.4动态规划--最大字段和。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

要好好学习这个难受难受超级难受的动态规划了，千万不要再沉迷在看剧和玩耍里面了。必须承认最近没有好好学习。

写在前面

最大字段和书上介绍了三种解法：暴力、递归分治、动态规划

递归分治，一分为二，合并的时候有三种情况，注意考虑清楚

动态规划，最优解的数组b[j]表示以数字a[j]为结尾的最大字段和。然后递推方程就是根据题目要求，什么时候，能根据前面的已知结果找到新的最大字段和。由上一状态推导到当前状态，有什么条件？？方法是什么？？

问题描述

给定n个整数(可能有负数)组成的序列a1，a2，...，an，求该序列的最大子段和，就是对于形如的子段和的最大值。如果所有整数都是负数，那么定义其最大子段和为0。

例如：（-2,11,-4,13,-5,-2）最大字段和是20，11+(-4)+13=20

问题分析

暴力解法

其实这个问题也可以用暴力方法求解，它的时间复杂度是O(n^2)

用数组a[]记录原始输入的n个元素，然后暴力循环（第一个循环i记录开始的位置，第二个循环j记录加多少个元素）遍历所有的情况，更新最优值

动态规划最大字段和,算法笔记,动态规划,算法

分治方法

分治法解题的一般步骤：

　　（1）分解，将要解决的问题划分成若干规模较小的同类问题；

　　（2）求解，当子问题划分得足够小时，用较简单的方法解决；

　　（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

序列a[1:n]可以分成长度相等的两段，a[1:n/2] a[n/2+1:n]

分别求出这两段的最大字段和，则合并的时候有三种情况：

A、a[1:n]的最大子段和与a[1:n/2]的最大子段和相同；

B、a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同；

C、a[1:n]的最大子段和在a[1:n/2]和a[n/2+1:n]各个去一小段拼接产生。

A、B这两种情形可递归求得。对于情形C，容易看出，a[n/2]与a[n/2+1]在最优子序列中。因此，我们可以在a[1:n/2]和a[n/2+1:n]中分别计算出如下的s1和s2。S1是子段a[1:n/2]从后往前加的最大值（包含a[n/2]），S2是子段a[n/2+1:n]从前往后加的最大值（包含a[n/2+1]），则s1+s2即为出现情形C使得最优值。

伪代码如下：

int MaxSubSum(int a, int left, int right){ 
int sum=0;
if (left==right) sum= a[left]>0?  a[left]:0;
else{
    int center=(left+right)/2; //计算中间值
//第一种情况算出来的leftsum
    int leftsum=MaxSubSum(a,left,center); 
//第二种情况算出来的rightsum
    int rightsum=MaxSubSum(a,center+1,right);
//算第三种情况的sum
    int s1=0;lefts=0;
//s1从后往前加，因为要包含a[n/2]
    for (int i=center;i>=left;i--){ 
        lefts+=a[i];
        if (lefts>s1) s1=lefts;
    }
    int s2=0;rights=0;
//s2从前往后加，因为要包含a[n/2+1]
    for (int i=center+1;i<=right;i++){ 
        rights+=a[i];
        if (rights>s2) s2=rights;
    }
//中间特殊段的sum
    sum=s1+s2;
    if (sum<leftsum) sum=leftsum;
    if (sum<rightsum) sum=rightsum;
  }
  return sum;
}

这个算法是典型的拆分成两个子问题，然后合并花费O（n）时间的问题

所以递归方程为： $动态规划最大字段和,算法笔记,动态规划,算法$ ，解这个递归方程（主定理）得，T(n)=O(nlogn)

动态规划方法

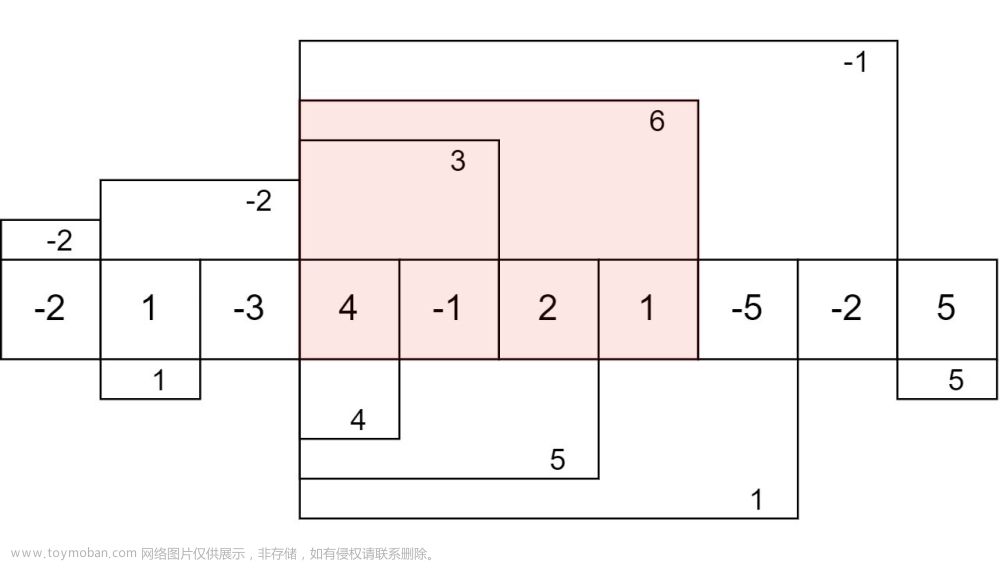
已知前n个数的最大子段和，那么前n+1个数的最大字段和有两种情况，一是包含前面的结果，二是不包含。序列a[]有n个数，我们就要做n次决策，从第一个数开始（下标从1开始），假设已经做好了前 i 个数的决策，并把做第 i 个数的最大子段和的结果保存到了b[i]（注意，前i个数的最大子段和sum和第i个数决策的子段和b[i]是不一样的，前者sum可能不包含第i个数，但第i个数决策的子段和b[i]一定包含b[i]，sum是当前最大子段的和，而b[i]是包含第i个数的子段和，并想办法使b[i]的值尽可能的大），当做第i+1个数的决策时，要做的工作就只是判断包含第i+1个数的子段和是否要把tem的值包进来，如果tem>0，就包括，否则不包括。
（再看一下总的想法）假设前n个数的最大子段和是b[n]，在决策前n+1个数的最大子段和时，判断b[n]的值，如果b[n]>0,那么前n+1个数的最大子段和为b[n]加上第n+1个数，否则就是第n+1个数自己。这里记住，你所求的是连续的几个数的和。

b[j]的定义，b[j]是指以a[j]结尾的最大子段和。因此有如下公式：

b[j] = max{b[j - 1] + a[j] , a[j]} 1=<j<=n

当bj-1>0时bj=bj-1+aj，否则bj=aj。由此可得计算bj的动态规划递归式bj=max{bj-1+aj，aj}，1≤j≤n。时间复杂度为O（n）

从递推公式我们可以写出最大字段和的动态规划算法，伪代码如下：

int MaxSum(int n, int *a){
\\bj[]的定义是以aj数字结尾的最大字段和
    int sum=0; b=0;
    for (i=1;i<=n;i++){
\\b就是bj,如果前面的数字都>0,就一直加,如果有<0的数字,就放弃前面一段,重新开始算
        if (b>0) b+=a[i]; else b=a[i];
\\每一次都判断,更新最大值
        if (b>sum) sum=b;
    }
    return sum;
}

代码如下：（精简版）

#include <iostream>
using namespace std;
const int maxN = 2e5 + 5;
int a[maxN];
int main() {
	int N, ans = -10000; cin >> N;
	for (int i = 1; i <= N; i++) {
		cin >> a[i];
		if (a[i - 1] > 0)
			a[i] += a[i - 1];
		ans = max(a[i], ans);
	}
	cout << ans;
}

代码如下：（思路清晰版）

#include <iostream>
using namespace std;
#define MAXN 30005
int a[MAXN];
int dp[MAXN];
int Max=0;
int maxsum(int n,int *a){
    dp[0]=0;
	for(int i=1;i<=n;++i)
	{
	    dp[i]=max(dp[i-1]+a[i],a[i]);
         //在i位置的情况可以分为：继承前面的所有数的总和+当前节点的和 或 仅选择当前节点
	    Max=max(Max,dp[i]);
	}
	return Max;
}
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int res=maxsum(n,a);
    cout << "res= " << res << endl;
    return 0;
}

输入输出样例

输入

5
83 223 -13 1331 -935

输出 1637

输入 #2

3
83 223 -13

输出 70

大致思路：题目是求连续两段的最大字段和，那么我们就可以从 1到n枚举，再从 n 到 1枚举，把每一段的最大字段和先标记一遍。

	for(ll i=1 ;i <= n; i++)
	{
		 scanf("%lld",&a[i]);
		 l[i]=max(l[i-1]+a[i],a[i]);
		 lf[i]=max(lf[i-1],l[i]);
	}
	for(ll i=n;i>=1;i--)
	{
		r[i]=max(r[i+1]+a[i],a[i]);
		rf[i]=max(rf[i+1],r[i]);
	}

由于求的是连续最大字段和，所以答案一定有一个分界点，那么我们接下来的任务就是找到这个分界点。所以我们从头到尾扫一遍，找出临界点，它左端的最大字段和，加上右端的最大字段和，即为答案。

	for(ll i=2;i<n;i++)
	{
		ans=max(lf[i-1]+rf[i+1],ans);
	}

AC代码：文章来源地址https://www.toymoban.com/news/detail-780742.html

#include <bits/stdc++.h>
using namespace std;
int n,a[1000010],head[1000010],tail[1000010],sum1[1000010],sum2[1000010],ans;
int main(){
	cin >> n;
    \\一定要记得初始化
    sum1[0]=sum2[n+1]=ans=-9999999;
	for(int i=1;i<=n;i++) cin >> a[i];
	//从前往后找最大子段和 
	for(int i=1;i<=n;i++){ 
        head[i]=max(head[i-1]+a[i],a[i]);
        sum1[i]=max(head[i],sum1[i-1]);
    }
	//从后往前找最大子段和 
	for(int i=n;i>=1;i--){
        tail[i]=max(tail[i+1]+a[i],a[i]);
        sum2[i]=max(sum2[i+1],tail[i]);
    }
	//枚举断点 
	for(int i=2;i<n;i++) ans=max(ans,sum1[i-1]+sum2[i+1]);
	cout << ans;
	return 0;
}

到了这里，关于3.4动态规划--最大字段和的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！