图解KMP算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了图解KMP算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

子串的定位操作通常称作串的模式匹配。你可以理解为在一篇英语文章中查找某个单词是否存在，或者说在一个主串中寻找某子串是否存在。

朴素的模式匹配算法

假设我们要从下面的主串S = "goodgoogle" 中，找到T = "google" 这个子串的位置。利用朴素的模式匹配算法我们通常需要下面的步骤。

(1)：主串S第一位开始，S与T前三个字母匹配成功，但S第四个字母是d而T的是g。第一位匹配失败。如下图所示：浅绿色方块代表匹配成功，红色方块代表匹配失败。

kmp算法图解过程,数据结构与算法,算法,c语言,c++,数据结构,开发语言,Powered by 金山文档

(2)：主串S从第二位开始，主串S首字母是o，要匹配的T的首字母是g。匹配失败：

(3)：主串S第三位开始，主串S首字母是o，要匹配的T首字母是g，匹配失败：

(4)：主串S第四位开始，主串S首字母是d，要匹配的T首字母是g，匹配失败：

(5)：主串S第五位开始，S与T，6个字母全部匹配，匹配成功：

简单来说，朴素的模式匹配算法就是对主串的每一位字符作为子串的开头，与要匹配的子串进行比较，如果匹配不成功，则主串需要回溯到与子串开始匹配的位置的下一个位置。

当子串与主串有较多的相等的字符时，这种算法的效率是极其低下的。例如：

KMP模式匹配算法

如果你忍受不了朴素的模式匹配算法。于是有三位前辈：D.E.Knuth，J.H.Morris和V.R.Pratt发表了一个模式匹配算法，可以大大避免重复遍历的情况，我们把他称之为克努特-莫里斯-普拉特算法，简称KMP算法。

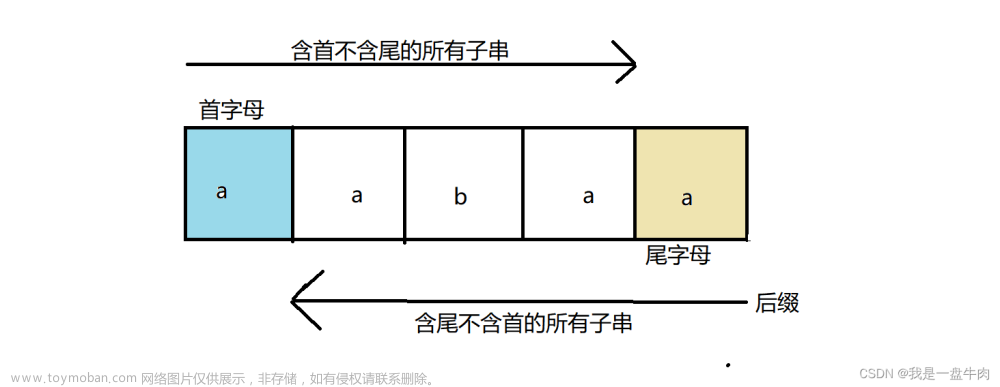
在去理解KMP算法时你需要知道一个字符串的前缀和后缀是什么？

下面以字符串 "google" 为例：

他的前缀集合：{ "g", "go", "goo", "goog", "googl" }。

它的后缀集合：{ "e", "le", "gle", "ogle", "oogle" }。

2.1 KMP算法匹配方式

假设我们要在主串S = "ABBABBABABAAABABAAA" 中查找模式串T = "ABBABAABABAA" 中的位置。

(1)：我们发现主串S和子串T的前5个字符均是匹配的，第6个字符是不匹配的。下一步我们肯定不能回溯到主串第二个字符的位置，不然就是在重走朴素的模式算法的道路了。我们观察发现：1：匹配了五个字符中，2：在模式串的左右两端有两个字符子串，他们是完全匹配的。我们称之为最长公共前后缀。

(2)：移动模式串，使得原来模式串的前缀到达模式串的后缀的位置：

这样的移动可以使得重新开始匹配的位置之前的字符，均是匹配的，因为公共前后缀AB是匹配的，并且原来的5个字符也是匹配的，所以将模式串的前缀移动到后缀的位置，与主串的后缀是匹配的。这样移动可以省去部分字符的不必要匹配（这样移动的正确性我们稍后探讨）。

(3)：我们发现模式串的移动与主串并没有关系，因为只是将模式串的前缀移动到了模式串的后缀的位置，并且已经匹配的字符与主串肯定是一样的撒。

这时我们对一般情况做出分析：

我们现在已经明白了为什么要移动模式串的前缀到后缀的位置，以及这样移动的正确性。

(4)：现在我们可以继续匹配一下主串，理解上述的操作：

2.2 next数组的手动推导

上面的图解以及分析仅是一个形象化的过程，我们还得将其转化为计算机能够处理的方式。

emm，我们假设存储字符串是从下标为1的位置开始的呢！

下面以具体的例子：主串S = "ABABABAABABAAABABAA"，模式串T = "ABABAAABABAA"，来分析如何转化成计算机能够处理的方式。

上面分析过，在模式串的移动过程中，与主串是没有关系的，我们只需要分析模式串即可：

模式串的任何一个位置都可能与主串发生不匹配，我们就是要将不匹配之后模式串由前缀移动到后缀的过程抽象成计算机能处理的形式。

我们发现有这样的规律：next数组对应的值是最长的公共前后缀加1。模式串剩余的字符就不再画图分析了，

我们将上面的数组取名为next数组，例如：我们发现模式串在与主串比较时，下标为5的位置发生了不匹配，我们只需要查找next[5] 的值，值为：3，就知道下一步是将模式串的3号位与主串的当前位置进行比较。

2.3 next数组的代码分析

/// <summary>
/// 求解next数组
/// </summary>
/// <param name="s"> 模式串的首字符地址 </param>
/// <param name="n"> 模式串的字符个数 </param>
/// <param name="next"> next数组的首元素地址 </param>
void getNext(char* s, int n, int* next)
{
    //遍历模式串
    int i = 1;
    //为next数组赋值
    int j = 0;
    //第一个字符不匹配将编号赋值为0，代表从主串的下一个位置开始比较
    next[1] = 0;
    while (i < n)
    {
        if (j == 0 || s[i] == s[j])
            next[++i] = ++j;
        else
            j = next[j];
    }
}

现在我们先以一个具体的例子来看代码是否正确哈，假设模式串为："abab"：

next[1] 需要一开始就初始化的哈。用i遍历模式串时，如果j指向的字符与i指向的字符相等，进入if分支，说明最长公共前后缀需要增加1，为什么是增加1呢？因为i一次只能遍历一个字符嘛！如果i指向的字符与j指向的字符不相等的话，进入else分支，令j=next[j]，即更新j的位置，将新的j指向的字符与i指向的字符进行比较，看是否相等，不相等继续令j=next[j]，直到j指向的字符与i指向的字符相等或者说j为0。为什么j的更新是j=next[j]? 我们下面就来分析原因！

这下你就能理解求next数组的全部代码啦。

2.4 查找子串的完整代码

下面是字符串从下标为1开始存储时的查找子串的代码。只是以一个具体的例子实践了一下，你只要理解了思路就随便写代码的。这里的代码仅供参考，具体代码还需结合题目具体分析！

/// <summary>
/// 求解next数组
/// </summary>
/// <param name="s"> 模式串的首字符地址 </param>
/// <param name="n"> 模式串的字符个数 </param>
/// <param name="next"> next数组的首元素地址 </param>
void getNext(char* s, int n, int* next)
{
    //i用来遍历模式串，j用来为next数组赋值，并且查找最长公共前后缀
    int i = 1, j = 0;
    //next[1]需要直接赋值
    next[1] = 0;
    while (i < n)
    {
        if (j == 0 || s[i] == s[j])
            next[++i] = ++j;
        else
            j = next[j];
    }
}
int main()
{
    char a[10] = " abababde";
    char s[5] = " aba";
    int next[4];
    getNext(s, 3, next);
    //8是主串的长度哈
    for (int i = 1, j = 0; i <= 8; i++)
    {
        while (j && a[i] != s[j+1])
            j = next[j];
        if (a[i] == s[j+1])
            j++;
        //3是模式串的字符个数，相等就代表找到了
        if (j == 3)
        {
            //输出开始匹配的位置
            printf("%d ", i - j + 1);
            //更新j尝试找到更多解
            j = next[j];
        }
    }
    return 0;
}

下面就是字符串从0开始存储的代码，同样的哈，代码版本有很多，重要的是理解思路！

void getNext(char* s, int n, int* next)
{
    int i = 0, j = -1;
    next[0] = -1;
    while (i < n)
    {
        if (j == -1 || s[i] == s[j])
            next[++i] = ++j;
        else
            j = next[j];
    }
}

int main()
{
    char a[9] = "abababde";
    char b[5] = "abab";

    int next[5];
    getNext(b, 4, next);
    for (int i = 0, j = 0; i < 8; i++)
    {
        while (j && a[i] != b[j])
            j = next[j];
        if (a[i] == b[j])
            j++;
        if (j == 4)
        {
            printf("%d ", i - j + 1);
            j = next[j];
        }
    }
    return 0;
}

小试牛刀

下面的题解法肯定不止一种，kmp算法也不一定是最简单的，但是阔以用来练习kmp算法的！

3.1 旋转字符串

796. 旋转字符串 - 力扣（LeetCode）

题目描述：给定两个字符串, s 和 goal。如果在若干次旋转操作之后，s 能变成 goal ，那么返回 true。
s 的旋转操作就是将 s 最左边的字符移动到最右边。
例如, 若 s = 'abcde'，在旋转一次之后结果就是'bcdea' 。

用kmp解题的大致思路就是拼接一个字符串到s后面，将goal当成模式串，在拼接后的字符串中查找goal就行。文章来源地址https://www.toymoban.com/news/detail-781019.html

void getNext(char* neddle, int n,int*next)
{
    int i =0;
    int j =-1;
    next[0] = -1;
    while(i<n)
    {
        if(j==-1||neddle[i]==neddle[j])
            next[++i] = ++j;
        else
            j = next[j];
    }
}
bool rotateString(char * s, char * goal){
    int lens = strlen(s);
    int leng = strlen(goal);
    if(lens!=leng)
        return false;
    char*str = (char*)calloc(lens*2+1, sizeof(char));
    memmove(str,s,lens);
    memmove(str+lens,s,lens);
    int * next = (int*)malloc(sizeof(int)*(leng+1));
    getNext(goal, leng,next);
    for(int i = 0,j=0;i<lens*2;i++)
    {
        while(j&&str[i]!=goal[j])
            j = next[j];
        if(str[i]==goal[j])
            j++;
        if(j==leng)
        {
            return true;
        }
    }
    return false;
}

3.2 最长快乐前缀

1392. 最长快乐前缀 - 力扣（LeetCode）

题目描述：
「快乐前缀」是在原字符串中既是非空前缀也是后缀（不包括原字符串自身）的字符串。
给你一个字符串 s，请你返回它的最长快乐前缀。如果不存在满足题意的前缀，则返回一个空字符串 "" 。

void getNext(char*s,int n,int* next)
{
    int i = 0;
    int j = -1;
    next[0] = -1;
    while(i<n)
    {
        if(j==-1||s[i]==s[j])
            next[++i] = ++j;
        else
            j = next[j];
    }
}

char * longestPrefix(char * s){
    int len = strlen(s);
    int next[len+1];
    getNext(s,len,next);
    int max = 0;
    if(next[len]>max)
        max = next[len];
    if(max==0)
        return "";
    else
    {
        char* ret = (char*)calloc(max+1,sizeof(char));
        for(int i = 0;i<max;i++)
        {
            ret[i] = s[i];
        }
        return ret;
    }
}