leetcode刷题之背包问题（01背包）-Toy模板网

这篇具有很好参考价值的文章主要介绍了leetcode刷题之背包问题（01背包）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

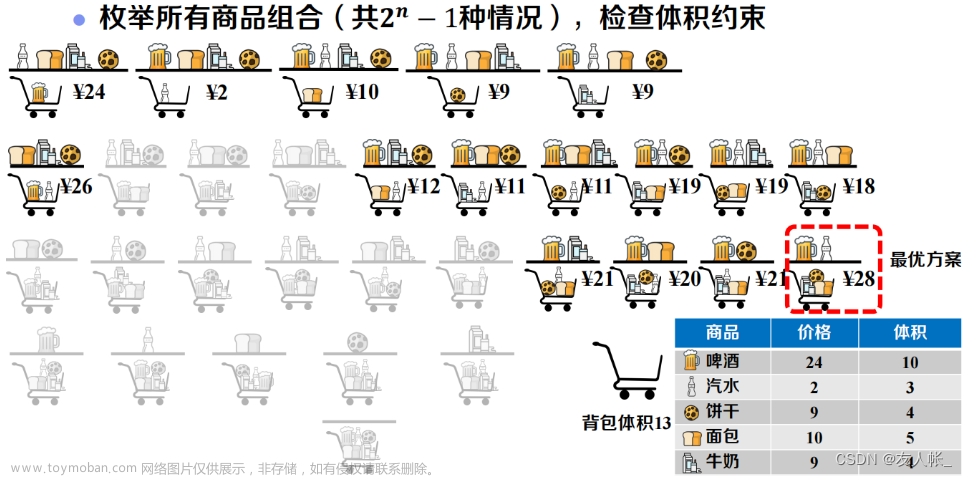
01 背包

概念：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是 $w e i g h t [i]$ ，得到的价值是 $v a l u e [i]$ 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

方法1：暴力回溯法

方法2：动态规划

三个物品，物品的重量分别为{1,3,4}，物品的价值分别为{15,20,30};背包最大容量为4。
leetcode 01背包,C++刷题,leetcode,动态规划,算法

（一）二维dp数组

确定dp数组以及下标的含义： $d p [i] [j]$ 代表从下标为[0,i]的物品中任意取，放到容量为j的背包里，价值总和最大是多少。
确定递推公式

不放物品i的最大价值： $d p [i - 1] [j]$
放物品i的最大价值（也就是背包容量减去物品i的容量所能放的最大价值加上物品 i 的价值）：
$d p [i - 1] [j - w e i g h t [i]]$ 为背包容量为 $j - w e i g h t [i]$ 的时候不放物品i的最大价值，那么 $d p [i - 1] [j - w e i g h t [i]] + v a l u e [i]$ （物品 $i$ 的价值）就是背包放物品 $i$ 得到的最大价值。
所以，递推公式为： $d p [i] [j] = ma x (d p [i - 1] [j], d p [i - 1] [j - w e i g h t [i]] + v a l u e [i])$

dp数组如何初始化
首先从 $d p [i] [j]$ 的定义出发，如果背包容量j为0的话，即 $d p [i] [0]$ ，无论是选取哪些物品，背包价值总和一定为0。如图:

初始化情况如下：

$d p [0] [j]$ 和 $d p [i] [0]$ 都已经初始化了，那么其他下标应该初始化多少呢？

其实从递归公式： $d p [i] [j] = ma x (d p [i - 1] [j], d p [i - 1] [j - w e i g h t [i]] + v a l u e [i])$ ; $d p [i - 1] [j] 和 d p [i - 1] [j - w e i g h t [i]]$ 分别在dp[i][j]的正上方和左上角方向，可以看出 $d p [i] [j]$ 是由左上方和正上方数值推导出来了，那么其他下标初始为什么数值都可以，因为都会被覆盖。

初始-1，初始-2，初始100，都可以！但只不过一开始就统一把dp数组统一初始为0会更方便一些，如下图所示。
leetcode 01背包,C++刷题,leetcode,动态规划,算法

// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
//weight.size()是指有多少物品也就是多少行，上一行是初始dp[i][j]全为0；
//bagweight是背包容量
for (int j = weight[0]; j <= bagweight; j++) 
{
    dp[0][j] = value[0];//初始化二维数组的第一行
}

确定遍历顺序（两层for循环）
先遍历物品还是先遍历背包重量呢？其实都可以！但是先遍历物品更好理解。
（1）先遍历物品

// weight数组的大小size 就是物品个数
for(int i = 1; i < weight.size(); i++) // 遍历物品
{ 
    for(int j = 0; j <= bagweight; j++) // 遍历背包容量
    { 
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
//当背包容量j小于物品i的重量weight[i]时，那就去掉物品i
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

（2）先遍历背包

// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) 
{ // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) 
    { // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

举例推导dp数组

void test() 
{
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagweight = 4;
    // 二维数组
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
    // 初始化
    for (int j = weight[0]; j <= bagweight; j++) 
    {
        dp[0][j] = value[0];
    }
    // weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) 
    { // 遍历物品
        for(int j = 0; j <= bagweight; j++) 
        { // 遍历背包容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
    cout << dp[weight.size() - 1][bagweight] << endl;
}

int main() 
{
    test();
}

（二）一维dp数组（滚动数组）

确定dp数组的定义：在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值最大为dp[j]。
一维dp数组的递推公式
dp[j]可以通过 $d p [j - w e i g h t [i]]$ 推导出来， $d p [j - w e i g h t [i]]$ 表示容量为 $j - w e i g h t [i]$ 的背包所背的最大价值。 $d p [j - w e i g h t [i]] + v a l u e [i]$ 表示容量为j - 物品i重量的背包加上物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即： $d p [j] ）$ 。
此时dp[j]有两个选择，一个是取dp[j]相当于二维dp数组中的 $d p [i - 1] [j]$ ，即不放物品i；一个是取 $d p [j - w e i g h t [i]] + v a l u e [i]$ ，即放物品i，指定是取最大的，毕竟是求最大价值。
所以，递推公式为： $d p [j] = ma x (d p [j], d p [j - w e i g h t [i]] + v a l u e [i])$ 。
可以看出相对于二维dp数组的写法，就是把dp[i][j]中i的维度去掉了。
一维dp数组如何初始化
dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
一维dp数组遍历顺序

for(int i = 0; i < weight.size(); i++) 
{ // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) 
    { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。倒序遍历是为了保证物品 i 只被放入一次！但如果一旦正序遍历了，那么物品0就会被重复加入多次！
5. 举例推导dp数组
一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下：
leetcode 01背包,C++刷题,leetcode,动态规划,算法文章来源地址https://www.toymoban.com/news/detail-781150.html

void test() 
{
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;
    // 初始化
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) 
    { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) 
        { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}
int main() 
{
    test();
}