极限运算法则——“高等数学”

1年前作者：认真学习的小雅兰.分类：Toy博客阅读(5)违法举报

这篇具有很好参考价值的文章主要介绍了极限运算法则——“高等数学”。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

各位CSDN的uu们你们好啊，今天，小雅兰学习的内容是极限运算法则

回顾

无穷小的极限运算法则

定理1：两个无穷小的和是无穷小

定理2：有界函数与无穷小的乘积是无穷小

极限的四则运算法则

定理3

定理4

定理5：极限的保序性

例题

1.多项式（有理整函数）的极限

2.有理分式函数的极限

复合函数的极限运算法则

极限运算法则小结

先回顾一下之前已经学过的知识——函数的极限

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学光靠函数的极限解题肯定是不够，存在着一定的局限性，所以我们就引出了一系列知识点

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

我们会学习到四则运算法则和复合函数极限运算法则

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

从左向右依次为：双极限问题、右极限问题、左极限问题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

上次课我们学到了无穷大与无穷小，了解到了无穷大与无穷小的关系：在自变量的同一变化过程下，如果f(x)为无穷大，则1/f(x)为无穷小，反之，如果f(x)为无穷小，且f(x)不等于0，则1/f(x) 为无穷大

我们的回顾就到这里结束啦，下面我们进入正题

一、无穷小的极限运算法则

定理1：两个无穷小的和是无穷小

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

这就是我们定理1的证明过程了，下面，我们趁热打铁，来看几道例题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学初学者很容易犯这样的错误，那么，正确的解法究竟是什么样子呢？

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

定理2：有界函数与无穷小的乘积是无穷小

我们来看一下证明过程

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

这就是我们的定理2的证明过程了，下面，我们还有几个推论

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

将推论2推广，可以得知：有限个无穷小的乘积也是无穷小

然后，我们再来看几个例题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

sin x是有界函数，1/x是无穷小，这个例题完全诠释出了有界函数与无穷小的乘积是无穷小

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

有的人会这样写

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

这样的写法是不严谨的，因为当x趋向于无穷时，sin x的极限不存在

看此例题，|cos 1/x |<=1,所以cos 1/x是一个有界函数，这又是一个有界函数与无穷小的乘积的问题

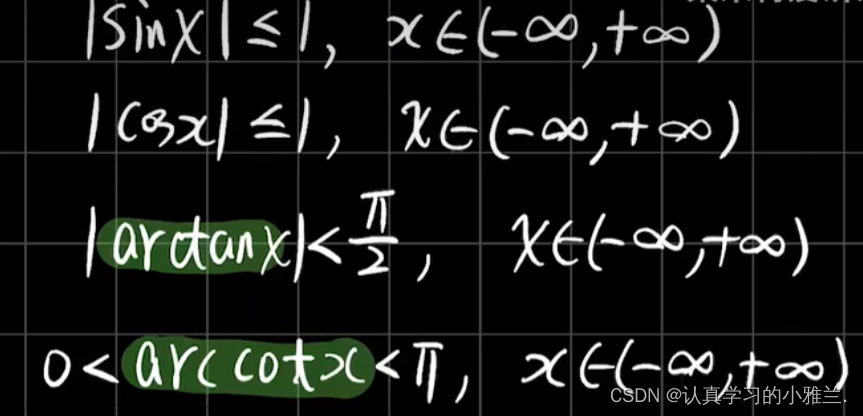
复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

再看一个例题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

经过上述学习，大家已经知道了两个无穷小的和、差、积都是无穷小，那么肯定有人想：两个无穷小的商是无穷小吗？

这个答案是否定的，相信大家可以看出，两个无穷小的商的极限的情况是非常复杂的

二、极限的四则运算法则

定理3

然后我们来证明一下(2)

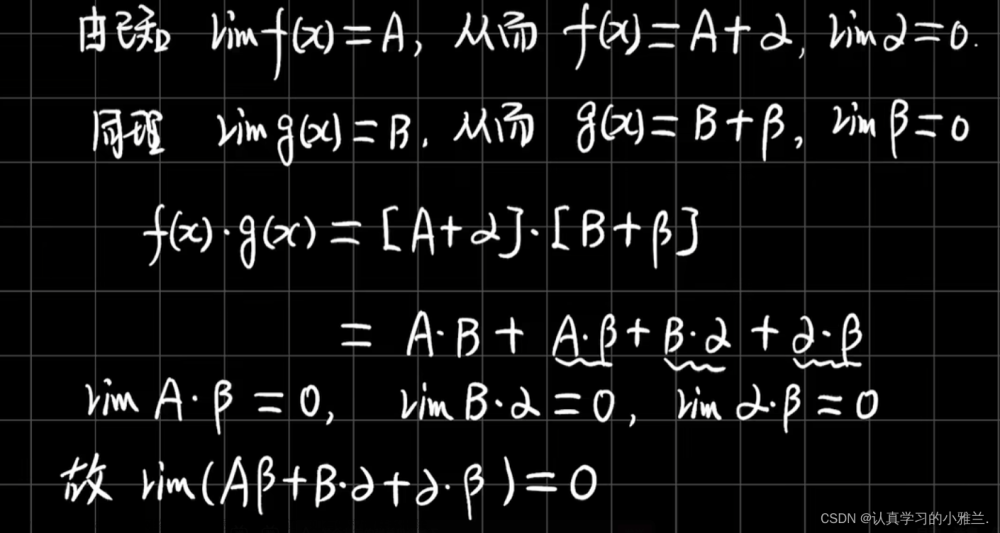
复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

这个A是一个常数函数，β是一个无穷小，常数函数与无穷小的乘积是无穷小，所以A乘以β的极限是无穷小；同理，B是一个常数函数，α是一个无穷小，那么B乘以α的极限也是无穷小。α是一个无穷小，β也是一个无穷小，两个无穷小的乘积是无穷小，所以α乘以β的乘积的极限是无穷小。

下面说明两点此定理的注意事项

（1）应用定理3时，要注意条件：lim f(x),limm g(x)均存在

下面来讲讲两个推论

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

定理4

定理5 （极限的保序性）

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

三、例题

1.多项式（有理整函数）的极限

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

来看几个简单的小题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

2.有理分式函数的极限

来看几个小例题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

结论

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

一般性结论

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学一个题目

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

这时要记住，千万不能把分子展开，这样计算量太大了！！！直接看三次项系数之比

四、复合函数的极限运算法则

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

例题

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

极限运算法则小结

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

复合函数的极限运算法则,高等数学,算法,学习,抽象代数,数学建模,几何学

好啦，那小雅兰今天学习的内容就到这里了，未来还要继续加油哟！！！文章来源地址https://www.toymoban.com/news/detail-781697.html

到了这里，关于极限运算法则——“高等数学”的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

C++学习笔记八：极限和数学运算<limits><cmath>
1） limits库： 1.1 源文档： https://en.cppreference.com/w/cpp/types/numeric_limits #include limits 1.2 库函数：函数解释：对于一个浮点数，lowest表示最小的可表示的负数，min表示最小的可表示的接近0的数，max表示最大的可表示的正数对于一个有符号整数，min表示可以表示的最小的负数，
2024年02月05日
浏览(9)
一元函数微分学中导数--定义--意义--基本公式--运算法则
目录导数的定义左导数和右导数导数的几何意义和物理意义几何意义导数的几何意义--切线的斜率物理意义导数的物理意义——瞬时速度基本初等函数导数公式基本初等函数常用基本初等函数导数公式导数求解的四则运算法则函数的求导法则复合函数求导法则
2024年02月11日
浏览(10)
高等数学(预备知识之反函数)
正弦函数 y = sin ⁡ x y=sin x y = sin x quad ( x ∈ [ − π 2 , π 2 ] xin[-frac{π}{2},frac{π}{2}] x ∈ [ − 2 π , 2 π ] )的反函数叫反正弦函数记作 y = arcsin ⁡ x y=arcsin x y = arcsin x , ( x ∈ [ − 1 , 1 ] xin[-1,1] x ∈ [ − 1 , 1 ] , y ∈ [ − π 2 , π 2 ] yin[-frac{π}{2},frac{π}{2}] y ∈ [ − 2 π
2024年02月07日
浏览(13)
高等数学(预备知识之幂函数)
幂函数 y=x a (a为常数, x为自变量) 例题1 : 判断下列是否为幂函数 (1) y=x 4 (2) y=2x 2 (3) y=2x (4) y=x 3 +2 (5) y=-x 2 只有第一个是对的, 严格意义上来讲,自变量前面不能有前缀和后缀 quad quad 性质: (1) : 图像都过(1,1)点 (2) : y=x a (a1或 a0) 当a为奇数时,y为奇函数, 当a为偶数时, y为偶函数
2024年02月16日
浏览(11)
高等数学(预备知识之三角函数)
正弦函数, 余弦函数, 正切函数都是以角为自变量 , 以单位圆上的坐标或坐标的比值为函数值的函数, 我们将他们称为三角函数 sin ⁡ sin sin α alpha α = y cos ⁡ cos cos α alpha α = x tan ⁡ tan tan α alpha α = y x frac{y}{x} x y 正弦函数: y= sin ⁡ sin sin x quad x ∈ in ∈ R 余弦函数
2024年02月13日
浏览(10)
高等工程数学 —— 第五章（4）罚函数法
外点罚函数法做题时就是构造一个 σ P sigma P σ P 然后计算两种情况的一阶必要条件未知量的值，若符合不等式约束就对其进行二阶必要条件验证。若成立就对 σ sigma σ 取无穷大然后得到最优解。例：这里求解 x ( σ ) x(sigma) x ( σ ) 时对于 x 1 + x 2 ≤ 4 x_1+x_2 leq 4 x 1 +
2024年02月03日
浏览(14)
【高等数学】多元函数-连续可导可微（定义+证明+记忆方法）
1.连续定义设二元函数 f ( P ) = f ( x , y ) f(P) = f(x,y) f ( P ) = f ( x , y ) 的定义域为D, P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P 0 ( x 0 , y 0 ) 为D的聚点，且 P 0 ∈ D P_0 in D P 0 ∈ D ,若 l i m ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 ) displaystyle lim_{(x,y)to(x_0,y_0)}f(x,y) = f(x_0,y_0) l i m ( x ,
2024年02月02日
浏览(29)
【高等数学基础知识篇】——一元函数微分学的应用
本文仅用于个人学习记录，使用的教材为汤家凤老师的《高等数学辅导讲义》。本文无任何盈利或者赚取个人声望的目的，如有侵权，请联系删除！极值点包括极大值点和极小值点。设y = f(x)在x = a处取极值，则f’(a) = 0或f’(a)不存在，反之不对。设f(x)可导且在x = a处取极值
2024年02月11日
浏览(12)
【高等数学】多元函数积分的轮换性，轮换对称性，对称性的区别
轮换性：只是单纯的自变量的符号形式发生交换，与轮换前的积分（包括被积函数和积分区域）没有本质区别注意到函数中x和y互换了，积分区域的横纵坐标也互换了，如果放在同一个坐标系下，蓝色区域和橙色区域是关于直线y=x对称的。轮换对称性：交换函数自变量的符号
2024年02月11日
浏览(42)
第七十天学习记录：高等数学：微分（宋浩板书）
sin(x+y) = sin(x)cos(y) + cos(x)sin(y)可以用三角形的几何图形来进行证明。假设在一个单位圆上，点A(x,y)的坐标为(x,y)，点B(x’, y’)的坐标为(x’, y’)。则以两点为直角的直角三角形的斜边长为1，且所在的角为夹角x+y。接下来，通过计算三角形中的各条边可以得到： sin(x+y) = y’
2024年02月08日
浏览(11)