SM2椭圆曲线公钥密码算法(Python实现)-Toy模板网

这篇具有很好参考价值的文章主要介绍了SM2椭圆曲线公钥密码算法(Python实现)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、实验目的（包括实验环境、实现目标等等）

1. 实验环境

Windows11
PyCharm2019.3.3 x64

2. 实现目标

通过编写代码实现SM2椭圆曲线公钥密码算法，加深对SM2椭圆曲线公钥密码算法的理解，体会该算法在解决实际问题的价值；
将密码学和数学知识相联系，并灵活运用到密码学的设计方案中；
提高实践能力和逻辑思维能力。

3. 实验中需要导入的库

random
math
gmssl

二、方案设计（包括背景、原理、必要的公式、图表、算法步骤等等）

1. 实验背景

SM2算法和RSA算法一样，同属于非对称算法体系，而且是椭圆曲线加密（ECC）算法的一种。但与RSA算法不同的是：RSA算法是基于大整数分解数学难题，SM2算法是基于椭圆曲线上点群离散对数难题。

相较于RSA算法，SM2算法的优点如下：

安全性高：192位的SM2密码强度已经比RSA的2048位密码强度要高，存储空间小。SM2算法的密码一般使用192~256位，RSA算法的密码一般需要2048~4096位。
签名速度快：SM2算法在私钥运算上的速度远大于RSA算法。
国产算法：由国家密码管理部门制订规范，不存在不可公开的密码。
目前普遍认为在国内被广泛使用的RSA的1024位算法不再安全，国家密码管理局下发了通知：自2011年7月1日起，投入运行并使用公钥密码的信息系统应使用SM2椭圆曲线公钥密码算法。

2. 实验原理

1. 素域Fp

当有限域Fq的q是奇素数时，素域Fp中的元素用整数0, 1, 2, …, p-1表示。其中：
加法单位元是整数0
乘法单位元是整数1
域元素的加法是整数的模p加法，即若a, b ∈ Fp，则a+b = (a+b) mod p;
域元素的乘法是整数的模p乘法，即若a, b ∈ Fp，则a·b = (a·b) mod p;

2. 素域Fp上的椭圆曲线

有限域Fq上的椭圆曲线是由点组成的集合。在仿射坐标系下，椭圆曲线上的点P（非无穷远点）的坐标表示为P = (x_p, y_p), 其中xp和p为满足一定方程的域元素，分别称为点P的x坐标和y坐标。
定义在Fp（p是大于3的素数）上的椭圆曲线方程为：
y² = x³ + ax + b, a,b ∈Fp,且(4a³ + 27b² )mod p ≠ 0
椭圆曲线E(Fp)定义为：
E(Fq) = {(x, y) | x, y ∈ Fp, 且满足上述方程} ∪ {O}, 其中O是无穷远点。
椭圆曲线E(Fp)上的点的数目用#E(Fq)表示，成为椭圆曲线E(Fp)的阶。

3. 必要的公式

1. Fp上的椭圆曲线群

椭圆曲线E(Fp)上的点按照下面的加法运算规则，构成一个交换群：

O + O = O;
∀P=(x,y)∈E(Fp ){O},P+O=P;
∀P=(x,y)∈E(Fp ){O},P的逆元素-P=(x,-y),P+(-P)=O;
两个非互逆的不同点相加的规则：
设P1 = (x₁, y₁) ∈ E(Fp)\{O}, P2 = (x₂, y₂) ∈ E(Fp)\{O}, 且 x₁ ≠ x₂
设P₃ = (x₃, y₃) = P₁ + P₂, 则x₃ = $\lambda$ ² - x₁ - x₂, y₃ = $\lambda$ (x₁ - x₃) - y₁
其中，λ= $\frac {y_2- y_1} {x_2- x_1}$

2. 倍点规则

设P1 = (x1, y1) ∈ E(Fp)\{O}, 且y1 ≠ 0, 设P3 = (x3, y3) = P1 + P2,
则x₃ = $\lambda$ ² - 2x₁, y₃ = $\lambda$ (x₁ - x₃) - y₁,
其中，λ= $\frac {3x_1^2 + a} {2y_1}$

3. 通过二进制展开法实现椭圆曲线多倍点运算

求点P的k倍点[k]P，将k用l长比特串形式表示k = $\sum_{j=0}^{l-1}$ k_j2^j, k∈{0, 1}

可按以下步骤进行求解：

置Q = O
j从l-1下降到0执行：Q = [2]Q
若kj = 1，则 Q = Q + P
执行结束后得到的Q即为P的k倍点

4. 算法步骤

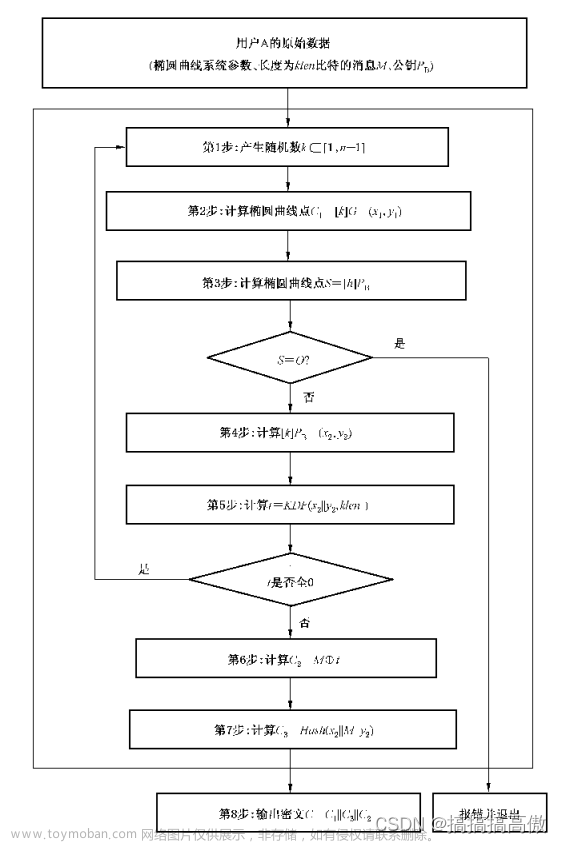
1. 加密算法

设需要发送的消息为比特串M，klen为M的比特长度。
为了对明文M进行加密，作为加密者的用户A应实现以下运算步骤：
A1：用随机数发生器产生随机数k∈[1,n-1]；
A2：计算椭圆曲线点C1=[k]G=(x1,y1)，将C1的数据类型转换为比特串；
A3：计算椭圆曲线点S=[h]PB，若S是无穷远点，则报错并退出；
A4：计算椭圆曲线点[k]PB=(x2,y2)，将坐标x2、y2 的数据类型转换为比特串；
A5：计算t=KDF(x2 || y2, klen)，若t为全0比特串，则返回A1；
A6：计算C2 = M ⊕ t；
A7：计算C3 = Hash(x2 || M || y2)；
A8：输出密文C = C1 || C2 || C3。

2. 解密算法

设klen为密文中C2的比特长度。
为了对密文C=C1 || C2 || C3 进行解密，作为解密者的用户B应实现以下运算步骤：
B1：从C中取出比特串C1，将C1的数据类型转换为椭圆曲线上的点，验证C1是否满足椭圆曲线方程，若不满足则报错并退出；
B2：计算椭圆曲线点S=[h]C1，若S是无穷远点，则报错并退出；
B3：计算[dB]C1=(x2,y2)，将坐标x2、y2的数据类型转换为比特串；
B4：计算t=KDF(x2 || y2, klen)，若t为全0比特串，则报错并退出；
B5：从C中取出比特串C2，计算M′ = C2 ⊕ t；
B6：计算u = Hash(x2 || M′ || y2)，从C中取出比特串C3，若u ≠ C3，则报错并退出；
B7：输出明文M′。

三、方案实现（包括算法流程图、主要函数的介绍、算法实现的主要代码等等）

1. 流程图

1. 加密算法流程图

python sm2,信息安全基础与密码学综合实验,python,算法

2. 解密算法流程图

python sm2,信息安全基础与密码学综合实验,python,算法

2. 主要函数

1. 数据类型转换

本部分所定义的函数实现了域元素、字节串、比特串、整数等数据类型的转换，方便计算与阅读。

def int_to_bytes(x, k)：实现整数到字节串的转换。接收非负整数x和字节串的目标长度k，k满足2^8k > x。返回值是长为k的字节串。注意字节串长度k是给定的参数！
def bytes_to_int(M)：字节串到整数的转换。接受长度为k的字节串。返回值是整数x。
def bits_to_bytes(s)：比特串到字节串的转换。接收长度为m的比特串s。返回长度为k的字节串M。其中k = [m/8] 向上取整。先判断字符串整体是否能正好转换为字节串，即长度是否为8的倍数。若不是则左填充至长度为8的倍数。
def bytes_to_bits(M)：字节串到比特串的转换。接收长度为k的字节串M，返回长度为m的比特串s，其中m = 8k。字节串逐位处理即可。
def fielde_to_bytes(e)：域元素到字节串的转换。域元素是整数，转换成字节串要明确长度。文档规定域元素转换为字节串的长度l是ceil(ceil(log(q, 2)/8))。接收的参数是域元素a，返回l长字节串M 。
def bytes_to_fielde(M)：字节串到域元素的转换。直接调用bytes_to_int( )。接收的参数是字节串M，返回域元素a。
def fielde_to_int(a)：域元素到整数的转换。域元素就是整数，直接返回即可。
def point_to_bytes§：点到字节串的转换。接收的参数是椭圆曲线上的点p，元组表示。输出字节串S。选用未压缩表示形式，即字节串s = PC + x + y，共1 + 2l个字节。
def bytes_to_point(s)：字节串到点的转换。接收的参数是字节串s，返回椭圆曲线上的点p，点P的坐标用元组表示。
附加数据类型转换。是上述几种数据类型转换的复合转换，或者是数制之间的转换。注意字符串的填充即可。共定义了def fielde_to_bits(a)、def point_to_bits§、def int_to_bits(x) 、def bytes_to_hex(m)、def bits_to_hex(s)、def hex_to_bits(h)、def hex_to_bytes(h)、def fielde_to_hex(e)几种函数。

2.辅助函数

本部分定义的函数是用于辅助实现SM2加解密算法中某些步骤的模块，这些模块若直接在加解密算法中会使代码变长造成阅读困难，因此将其定义为单独的函数以使结构清晰。

def add_point(P, Q, p)：椭圆曲线上的点加运算。接收的参数是元组P和Q，表示相加的两个点，p为模数。返回二者的点加和。
def double_point(P, p, a): 二倍点算法。不能直接用点加算法，否则会发生除零错误。接收的参数是点P，素数p，椭圆曲线参数a。返回P的二倍点。
def mult_point(P, k, p, a)：多倍点算法。通过二进制展开法实现。接收的参数[k]p是要求的多倍点，m是模数，a是椭圆曲线参数。
def frac_to_int(up, down, p)：将分式模运算转换为整数。输入 up/down mod m, 返回该分式在模m意义下的整数。点加和二倍点运算时求λ用。
def calc_inverse(M, m)：模逆算法。返回M模m的逆。在将分式模运算转换为整数时用，分子分母同时乘上分母的模逆。
def on_curve(args, P)：验证某个点是否在椭圆曲线上。接收的参数是椭圆曲线系统参数args和要验证的点P(x, y)。
def KDF(Z, klen)：密钥派生函数KDF。接收的参数是比特串Z和要获得的密钥数据的长度klen。返回klen长度的密钥数据比特串K。

3. 加解密算法

本部分是加解密的两个函数。

def encry_sm2(args, PB, M)：加密算法。接收的参数是椭圆曲线系统参数args(p, a, b, h, G, n)。其中n是基点G的阶。PB是B的公钥，M是明文消息。
def decry_sm2(args, dB, C)：解密算法。接收的参数为椭圆曲线系统参数args(p, a, b, h, G, n)。dB是B的私钥，C是密文消息。

4. 参数获取

本部分的函数用于获取算法使用的相关数据。

def get_args( )：椭圆曲线系统参数args(p, a, b, h, G, n)的获取。
def get_key( )：密钥获取。本程序中主要是消息接收方B的公私钥的获取。

3. Python代码

import random
from math import gcd, ceil, log
from gmssl import sm3


# 数据类型装换
# 整数到字节串的转换。接收非负整数x和字节串的目标长度k，k满足2^8k > x。返回值是长为k的字节串。k是给定的参数。
def int_to_bytes(x, k):         # 整体思路是先左填充0将x变为k*8位16进制数串，再每2位合成1个字节
    if pow(256, k) <= x:
        raise Exception("无法实现整数到字节串的转换，目标字节串长度过短！")
    s = hex(x)[2:].rjust(k*2, '0')          # s是k*2位十六进制串
    M = b''
    for i in range(k):
        M = M + bytes([eval('0x' + s[i*2:i*2+2])])
    return M


# 字节串到整数的转换。接受长度为k的字节串。返回值是整数x
def bytes_to_int(M):            # 整体思路是从后向前遍历M，每个字节的基数是2^8。
    k = len(M)          # k是字节串的长度
    x = 0           # x存储最后的整数
    for i in range(k-1, -1, -1):
        x += pow(256, k-1-i) * M[i]
    return x


# 比特串到字节串的转换。接收长度为m的比特串s。返回长度为k的字节串M。其中k = [m/8] 向上取整。
def bits_to_bytes(s):           # 先判断字符串整体是否能正好转换为字节串，即长度是否为8的倍数。若不是则左填充至长度为8的倍数。
    k = ceil(len(s)/8)          # 比特串长度除以8向上取整
    s = s.rjust(k*8, '0')           # 若能整除这一步相当于没有，若不能则相当于将其左填充为长度能被8整除得k
    M = b''         # M存储要返回的字节串
    for i in range(k):
        M = M + bytes([eval('0b' + s[i*8: i*8+8])])
    return M


# 字节串到比特串的转换。接收长度为k的字节串M，返回长度为m的比特串s，其中m = 8k。字节串逐位处理即可。
def bytes_to_bits(M):           # 整体思路是把每个字节变为8位比特串，用列表存储，最后连接起来
    s_list = []
    for i in M:
        s_list.append(bin(i)[2:].rjust(8, '0'))         # 每次循环存储1个字节。左填充补0
    s = ''.join(s_list)
    return s


# 域元素到字节串的转换。域元素是整数，转换成字节串要明确长度。文档规定域元素转换为字节串的长度是ceil(ceil(log(q, 2)/8))。接收的参数是域元素a，返回字节串M
def fielde_to_bytes(e):
    q = eval('0x' + '8542D69E 4C044F18 E8B92435 BF6FF7DE 45728391 5C45517D 722EDB8B 08F1DFC3'.replace(' ', ''))
    t = ceil(log(q, 2))
    l = ceil(t / 8)
    return int_to_bytes(e, l)


# 字节串到域元素的转换。直接调用bytes_to_int()。接收的参数是字节串M，返回域元素a
def bytes_to_fielde(M):         # 域元素不用填充
    return bytes_to_int(M)


# 域元素到整数的转换
def fielde_to_int(a):           # 直接返回
    return a


# 点到字节串的转换。接收的参数是椭圆曲线上的点p，元组表示。输出字节串S。选用未压缩表示形式
def point_to_bytes(P):
    xp, yp = P[0], P[1]
    x = fielde_to_bytes(xp)
    y = fielde_to_bytes(yp)
    PC = bytes([0x04])
    s = PC + x + y
    return s


# 字节串到点的转换。接收的参数是字节串s，返回椭圆曲线上的点P，点P的坐标用元组表示
def bytes_to_point(s):
    if len(s) % 2 == 0:
        raise Exception("无法实现字节串到点的转换，请检查字节串是否为未压缩形式！")
    l = (len(s) - 1) // 2
    PC = s[0]
    if PC != 4:
        raise Exception("无法实现字节串到点的转换，请检查PC是否为b'04'！")
    x = s[1: l+1]
    y = s[l+1: 2*l+1]
    xp = bytes_to_fielde(x)
    yp = bytes_to_fielde(y)
    P = (xp, yp)            # 此处缺少检验点p是否在椭圆曲线上
    return P


# 附加数据类型转换
# 域元素到比特串
def fielde_to_bits(a):
    a_bytes = fielde_to_bytes(a)
    a_bits = bytes_to_bits(a_bytes)
    return a_bits


# 点到比特串
def point_to_bits(P):
    p_bytes = point_to_bytes(P)
    p_bits = bytes_to_bits(p_bytes)
    return p_bits


# 整数到比特串
def int_to_bits(x):
    x_bits = bin(x)[2:]
    k = ceil(len(x_bits)/8)         # 8位1组，k是组数。目的是方便对齐
    x_bits = x_bits.rjust(k*8, '0')
    return x_bits


# 字节串到十六进制串
def bytes_to_hex(m):
    h_list = []         # h_list存储十六进制串中的每一部分
    for i in m:
        e = hex(i)[2:].rjust(2, '0')            # 不能把0丢掉
        h_list.append(e)
    h = ''.join(h_list)
    return h


# 比特串到十六进制
def bits_to_hex(s):
    s_bytes = bits_to_bytes(s)
    s_hex = bytes_to_hex(s_bytes)
    return s_hex


# 十六进制串到比特串
def hex_to_bits(h):
    b_list = []
    for i in h:
        b = bin(eval('0x' + i))[2:].rjust(4, '0')           # 增强型for循环，是i不是h
        b_list.append(b)
    b = ''.join(b_list)
    return b


# 十六进制到字节串
def hex_to_bytes(h):
    h_bits = hex_to_bits(h)
    h_bytes = bits_to_bytes(h_bits)
    return h_bytes


# 域元素到十六进制串
def fielde_to_hex(e):
    h_bytes = fielde_to_bytes(e)
    h = bytes_to_hex(h_bytes)
    return h


# 密钥派生函数KDF。接收的参数是比特串Z和要获得的密钥数据的长度klen。返回klen长度的密钥数据比特串K
def KDF(Z, klen):
    v = 256           # 密码杂凑函数采用SM3
    if klen >= (pow(2, 32) - 1) * v:
        raise Exception("密钥派生函数KDF出错，请检查klen的大小！")
    ct = 0x00000001
    if klen % v == 0:
        l = klen // v
    else:
        l = klen // v + 1
    Ha = []
    for i in range(l):         # i从0到 klen/v-1（向上取整）,共l个元素
        s = Z + int_to_bits(ct).rjust(32, '0')         # s存储 Z || ct 的比特串形式 # 注意，ct要填充为32位
        s_bytes = bits_to_bytes(s)          # s_bytes存储字节串形式
        s_list = [i for i in s_bytes]
        hash_hex = sm3.sm3_hash(s_list)
        hash_bin = hex_to_bits(hash_hex)
        Ha.append(hash_bin)
        ct += 1
    if klen % v != 0:
        Ha[-1] = Ha[-1][:klen - v*(klen//v)]
    k = ''.join(Ha)
    return k


# 模逆算法。返回M模m的逆。在将分式模运算转换为整数时用，分子分母同时乘上分母的模逆。
def calc_inverse(M, m):
    if gcd(M, m) != 1:
        return None
    u1, u2, u3 = 1, 0, M
    v1, v2, v3 = 0, 1, m
    while v3 != 0:
        q = u3 // v3
        v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
    return u1 % m


# 将分式模运算转换为整数。输入 up/down mod m, 返回该分式在模m意义下的整数。点加和二倍点运算时求λ用。
def frac_to_int(up, down, p):
    num = gcd(up, down)
    up //= num
    down //= num         # 分子分母约分
    return up * calc_inverse(down, p) % p


# 椭圆曲线上的点加运算。接收的参数是元组P和Q，表示相加的两个点，p为模数。返回二者的点加和
def add_point(P, Q, p):
    if P == 0:
        return Q
    if Q == 0:
        return P
    x1, y1, x2, y2 = P[0], P[1], Q[0], Q[1]
    e = frac_to_int(y2 - y1, x2 - x1, p)            # e为λ
    x3 = (e*e - x1 - x2) % p            # 注意此处也要取模
    y3 = (e * (x1 - x3) - y1) % p
    ans = (x3, y3)
    return ans


# 二倍点算法。不能直接用点加算法，否则会发生除零错误。接收的参数是点P，素数p，椭圆曲线参数a。返回P的二倍点。
def double_point(P, p, a):
    if P == 0:
        return P
    x1, y1 = P[0], P[1]
    e = frac_to_int(3 * x1 * x1 + a, 2 * y1, p)         # e是λ
    x3 = (e * e - 2 * x1) % p         # 取模！！！！！
    y3 = (e * (x1 - x3) - y1) % p
    Q = (x3, y3)
    return Q


# 多倍点算法。通过二进制展开法实现。接收的参数[k]p是要求的多倍点，m是模数，a是椭圆曲线参数。
def mult_point(P, k, p, a):
    s = bin(k)[2:]          # s是k的二进制串形式
    Q = 0
    for i in s:
        Q = double_point(Q, p, a)
        if i == '1':
            Q = add_point(P, Q, p)
    return Q


# 验证某个点是否在椭圆曲线上。接收的参数是椭圆曲线系统参数args和要验证的点P(x, y)。
def on_curve(args, P):
    p, a, b, h, G, n = args
    x, y = P
    if pow(y, 2, p) == ((pow(x, 3, p) + a*x + b) % p):
        return True
    return False


# 加密算法。接收的参数是椭圆曲线系统参数args(p, a, b, h, G, n)。其中n是基点G的阶。PB是B的公钥，M是明文消息。
def encry_sm2(args, PB, M):
    p, a, b, h, G, n = args         # 序列解包
    M_bytes = bytes(M, encoding='ascii')
    print("A1：用随机数发生器产生随机数k∈[1,n-1]")
    k = random.randint(1, n-1)
    k_hex = hex(k)[2:]          # k_hex 是k的十六进制串形式
    print("生成的随机数是：", k_hex)
    print("\nA2:计算椭圆曲线点C1=[k]G=(x1,y1)，将C1的数据类型转换为比特串")
    C1 = mult_point(G, k, p, a)
    print("椭圆曲线点C1=[k]G=(x1,y1)的坐标是:", tuple(map(hex, C1)))
    C1_bits = point_to_bits(C1)
    print("椭圆曲线点C1=[k]G=(x1,y1)的坐标的比特串形式是:", C1_bits)
    print("\nA3：计算椭圆曲线点S = [h]PB")
    S = mult_point(PB, h, p, a)
    if S == 0:
        raise Exception("计算得到的S是无穷远点")
    print("A3椭圆曲线点S = [h]PB的坐标是:", tuple(map(hex, S)))
    print("\nA4：计算椭圆曲线点[k]PB=(x2,y2)，将坐标x2、y2 的数据类型转换为比特串")
    x2, y2 = mult_point(PB, k, p, a)
    print("椭圆曲线点[k]PB=(x2,y2)的坐标是:", tuple(map(hex, (x2, y2))))
    x2_bits = fielde_to_bits(x2)
    print("x2的比特串形式是：", x2_bits)
    y2_bits = fielde_to_bits(y2)
    print("y2的比特串形式是：", y2_bits)
    print("\nA5：计算t=KDF(x2 ∥ y2, klen)，若t为全0比特串，则返回A1")
    M_hex = bytes_to_hex(M_bytes)
    klen = 4 * len(M_hex)
    print("明文消息的比特串长度klen是：", klen)
    t = KDF(x2_bits + y2_bits, klen)
    print("通过KDF算法计算得到的t=KDF(x2 ∥ y2, klen)是：", t)
    if eval('0b' + t) == 0:
        raise Exception("KDF返回了全零串，请检查KDF算法！")
    t_hex = bits_to_hex(t)
    print("t的十六进制表示形式是：", t_hex)
    print("\nA6：计算计算C2 = M ⊕ t")
    C2 = eval('0x' + M_hex + '^' + '0b' + t)
    print("计算的C2是：", hex(C2)[2:])
    print("\nA7：计算C3 = Hash(x2 ∥ M ∥ y2)")
    x2_bytes = bits_to_bytes(x2_bits)
    y2_bytes = bits_to_bytes(y2_bits)
    hash_list = [i for i in x2_bytes + M_bytes + y2_bytes]
    C3 = sm3.sm3_hash(hash_list)
    print("计算的C3 = Hash(x2 ∥ M ∥ y2)是：", C3)
    print("\nA8：输出密文C = C1 ∥ C2 ∥ C3")
    C1_hex = bits_to_hex(C1_bits)
    C2_hex = hex(C2)[2:]
    C3_hex = C3
    C_hex = C1_hex + C2_hex + C3_hex
    print("加密得到的密文是：", C_hex)
    return C_hex


# 解密算法。接收的参数为椭圆曲线系统参数args(p, a, b, h, G, n)。dB是B的私钥，C是密文消息。
def decry_sm2(args, dB, C):
    p, a, b, h, G, n = args
    print("B1：从C中取出比特串C1，将C1的数据类型转换为椭圆曲线上的点，验证C1是否满足椭圆曲线方程，若不满足则报错并退出；")
    l = ceil(log(p, 2)/8)         # l是一个域元素（比如一个点的横坐标）转换为字节串后的字节长度.则未压缩的形式下秘闻第一部分C1长度为2l+1
    bytes_l1 = 2*l+1
    print("计算得到的C1的字节串长度是：", bytes_l1)
    hex_l1 = bytes_l1 * 2            # hex_l1是密文第一部分C1的十六进制串的长度
    C_bytes = hex_to_bytes(C)
    print("将十六进制密文串转换为字节串是：", C_bytes)
    C1_bytes = C_bytes[0:2*l+1]
    print("从密文字节串中取出的C1的字节串是：", C1_bytes)
    C1 = bytes_to_point(C1_bytes)
    print("将C1字节串转换为椭圆曲线上的点是：", C1)
    if not on_curve(args, C1):          # 检验C1是否在椭圆曲线上
        raise Exception("在解密算法B1中，取得的C1不在椭圆曲线上！")
    x1, y1 = C1[0], C1[1]
    x1_hex, y1_hex = fielde_to_hex(x1), fielde_to_hex(y1)
    print("C1坐标用的十六进串形式表示是：", (x1_hex, y1_hex))
    print("\nB2：计算椭圆曲线点S=[h]C1，若S是无穷远点，则报错并退出；")
    S = mult_point(C1, h, p, a)
    print("计算得到的S是：", S)
    if S == 0:
        raise Exception("在解密算法B2中，S是无穷远点！")
    xS, yS = S[0], S[1]
    xS_hex, yS_hex = fielde_to_hex(xS), fielde_to_hex(yS)
    print("S的坐标用十六进制串形式表示是：", (xS_hex, yS_hex))
    print("\nB3：计算[dB]C1=(x2,y2)，将坐标x2、y2的数据类型转换为比特串；")
    temp = mult_point(C1, dB, p, a)
    x2, y2 = temp[0], temp[1]
    x2_hex, y2_hex = fielde_to_hex(x2), fielde_to_hex(y2)
    print("解密得到的[dB]C1=(x2,y2)的十六进制串形式是：", (x2_hex, y2_hex))
    print("\nB4:计算t=KDF(x2 ∥ y2, klen)，若t为全0比特串，则报错并退出；")
    hex_l3 = 64           # hex_l3是密文第三部分C3的十六进制串的长度。C3是通过SM3得到的hash值，是64位十六进制串。
    hex_l2 = len(C) - hex_l1 - hex_l3           # hex_l2是密文第二部分C2的十六进制串的长度。
    klen = hex_l2 * 4           # klen是密文C2中比特串的长度
    print("计算的C2的比特串长度klen是：", klen)
    x2_bits, y2_bits = hex_to_bits(x2_hex), hex_to_bits(y2_hex)
    t = KDF(x2_bits + y2_bits, klen)
    print("计算的t=KDF(x2 ∥ y2, klen)是：", t)
    if eval('0b' + t) == 0:
        raise Exception("在解密算法B4中，得到的t是全0串！")
    t_hex = bits_to_hex(t)
    print("t的十六进制串形式是：", t_hex)
    print("\nB5：从C中取出比特串C2，计算M′ = C2 ⊕ t；")
    C2_hex = C[hex_l1: -hex_l3]
    print("C2的十六进制串形式是：", C2_hex)
    M1 = eval('0x' + C2_hex + '^' + '0x' + t_hex)           # M1是M'，M′ = C2 ⊕ t
    M1_hex = hex(M1)[2:].rjust(hex_l2, '0')         # 注意位数要一致
    print("计算的M′ = C2 ⊕ t是：", M1_hex)
    print("\nB6：计算u = Hash(x2 ∥ M′ ∥ y2)，从C中取出比特串C3，若u != C3，则报错并退出；")
    M1_bits = hex_to_bits(M1_hex)
    cmp_bits = x2_bits + M1_bits + y2_bits          # cmp_bits存储用于计算哈希值以对比C3的二进制串
    cmp_bytes = bits_to_bytes(cmp_bits)
    cmp_list = [i for i in cmp_bytes]
    u = sm3.sm3_hash(cmp_list)          # u中存储
    print("计算的u = Hash(x2 ∥ M′ ∥ y2)是：", u)
    C3_hex = C[-hex_l3:]
    print("从C中取出的C3的十六进制形式是：", C3_hex)
    if u != C3_hex:
        raise Exception("在解密算法B6中，计算的u与C3不同！")
    print("\nB7：输出明文M′")
    M_bytes = hex_to_bytes(M1_hex)
    M = str(M_bytes, encoding='ascii')
    print("解密出的明文是：", M)
    return M


# 椭圆曲线系统参数args(p, a, b, h, G, n)的获取。
def get_args():
    p = eval('0x' + '8542D69E 4C044F18 E8B92435 BF6FF7DE 45728391 5C45517D 722EDB8B 08F1DFC3'.replace(' ', ''))
    a = eval('0x' + '787968B4 FA32C3FD 2417842E 73BBFEFF 2F3C848B 6831D7E0 EC65228B 3937E498'.replace(' ', ''))
    b = eval('0x' + '63E4C6D3 B23B0C84 9CF84241 484BFE48 F61D59A5 B16BA06E 6E12D1DA 27C5249A'.replace(' ', ''))
    h = 1
    xG = eval('0x' + '421DEBD6 1B62EAB6 746434EB C3CC315E 32220B3B ADD50BDC 4C4E6C14 7FEDD43D'.replace(' ', ''))
    yG = eval('0x' + '0680512B CBB42C07 D47349D2 153B70C4 E5D7FDFC BFA36EA1 A85841B9 E46E09A2'.replace(' ', ''))
    G = (xG, yG)            # G 是基点
    n = eval('0x' + '8542D69E 4C044F18 E8B92435 BF6FF7DD 29772063 0485628D 5AE74EE7 C32E79B7'.replace(' ', ''))
    args = (p, a, b, h, G, n)           # args是存储椭圆曲线参数的元组。
    return args


# 密钥获取。本程序中主要是消息接收方B的公私钥的获取。
def get_key():
    xB = eval('0x' + '435B39CC A8F3B508 C1488AFC 67BE491A 0F7BA07E 581A0E48 49A5CF70 628A7E0A'.replace(' ', ''))
    yB = eval('0x' + '75DDBA78 F15FEECB 4C7895E2 C1CDF5FE 01DEBB2C DBADF453 99CCF77B BA076A42'.replace(' ', ''))
    PB = (xB, yB)           # PB是B的公钥
    dB = eval('0x' + '1649AB77 A00637BD 5E2EFE28 3FBF3535 34AA7F7C B89463F2 08DDBC29 20BB0DA0'.replace(' ', ''))
    # dB是B的私钥
    key_B = (PB, dB)
    return key_B


print("SM2椭圆曲线公钥密码算法".center(100, '='))
print("本算法采用256位素数域上的椭圆曲线。椭圆曲线方程为：")
print("y^2 = x^3 + ax + b")

print("此为算法第1部分，获取相关数据".center(100, '='))
# 这里作为后续加解密算法参数的是元组args和key_B，ascii字符串明文消息M。均为不可变序列。在这一部分用于输出时不会改变其值
print("下面获取椭圆曲线系统参数")
args = get_args()           # 获取椭圆曲线系统参数
p, a, b, h, G, n = args         # 序列解包
p, a, b, h, xG, yG, n = tuple(map(lambda a: hex(a)[2:], (p, a, b, h, G[0], G[1], n)))   # 将参数转换为十六进制串便于输出
print("椭圆曲线系统所在素域的p是：", p)
print("椭圆曲线系统的参数a是：", a)
print("椭圆曲线系统的参数b是：", b)
print("椭圆曲线系统的余因子h是：", h)
print("椭圆曲线系统的基点G的横坐标xG是：", xG)
print("椭圆曲线系统的基点G的纵坐标yG是：", yG)

print("下面获取接收方B的公私钥")
key_B = get_key()           # 设置消息接收方的公私钥
PB, dB = key_B          # 序列解包，PB是公钥，是以元组形式存储的点(xB, yB), dB是私钥，是整数
xB, yB, dB = tuple(map(lambda a: hex(a)[2:], (PB[0], PB[1], dB)))
print("接收方B的公钥PB的横坐标xB是：", xB)
print("接收方B的公钥PB的纵坐标yB是：", yB)
print("接收方B的私钥dB是：", dB)
print("下面获取明文")
M = input('请输入要加密的明文(明文应为ascii字符组成的字符串)：')
print("获取的ascii字符串明文是：", M)
print("此为算法第2部分，加密部分".center(100, '='))
C = encry_sm2(args, key_B[0], M)            # 加密算法的参数是椭圆系统参数，B的公钥PB，ascii字符串形式的明文消息M。返回十六进制串形式的密文消息

print("此为算法第3部分，解密部分".center(100, '='))
de_M = decry_sm2(args, key_B[1], C)           # 解密算法的参数是椭圆曲线系统参数，B的私钥dB，十六进制串形式的密文消息。返回ascii字符串形式的明文消息M

print("此为算法第4部分，验证部分".center(100, '='))
print("原始明文是：", M)
print("解密得到的明文是：", de_M)
if M == de_M:
    print("恭喜您，解密成功！")
else:
    print("解密失败，请检查算法！")

四、数据分析(包括算法测试数据的分析，运行结果截图等等)

椭圆曲线系统所在素域的p是：
8542d69e4c044f18e8b92435bf6ff7de457283915c45517d722edb8b08f1dfc3
椭圆曲线系统的参数a是：
787968b4fa32c3fd2417842e73bbfeff2f3c848b6831d7e0ec65228b3937e498
椭圆曲线系统的参数b是：
63e4c6d3b23b0c849cf84241484bfe48f61d59a5b16ba06e6e12d1da27c5249a
椭圆曲线系统的余因子h是：
1
椭圆曲线系统的基点G的横坐标xG是：
421debd61b62eab6746434ebc3cc315e32220b3badd50bdc4c4e6c147fedd43d
椭圆曲线系统的基点G的纵坐标yG是：
680512bcbb42c07d47349d2153b70c4e5d7fdfcbfa36ea1a85841b9e46e09a2
接收方B的公钥PB的横坐标xB是：
435b39cca8f3b508c1488afc67be491a0f7ba07e581a0e4849a5cf70628a7e0a
接收方B的公钥PB的纵坐标yB是：
75ddba78f15feecb4c7895e2c1cdf5fe01debb2cdbadf45399ccf77bba076a42
接收方B的私钥dB是：
1649ab77a00637bd5e2efe283fbf353534aa7f7cb89463f208ddbc2920bb0da0

样例:要加密的明文为字符串“encryption standard”。对其进行加解密
程序第1部分，获取参数。程序获取加解密所需的相关数据并回显到屏幕上，如图所示：
python sm2,信息安全基础与密码学综合实验,python,算法
程序第2部分，加密部分。按照文档所给步骤对明文进行加密。其中步骤A1-A5如图所示：

步骤A6-A8如图所示：

加密得到的密文的十六进制形式是：

040e8f6a6a306d42ff2ce2220735fc32df125b4849398d30953daa7aeb392a6cd70188211d55c6754e73fd6487b3b2af933d2f83ea8ede155834787da752338a13b9f51200a9eced22a5fdabd9dd912b006471e2558a1fd525a3dc8680ce18f17d7546b500832586af771c16ce9441cb81d96dc8

程序第3部分，解密部分。按照文档所给步骤对密文进行解密。其中步骤B1-B4如图所示：
python sm2,信息安全基础与密码学综合实验,python,算法
步骤B5-B7如图所示：

解密得到的明文是：encryption standard

程序第4部分，验证部分。将原始明文与解密得到的明文进行比较，若二者相同则表明解密成功。
解密成功，结果如图所示：
python sm2,信息安全基础与密码学综合实验,python,算法
至此，实验结束。文章来源地址https://www.toymoban.com/news/detail-781949.html