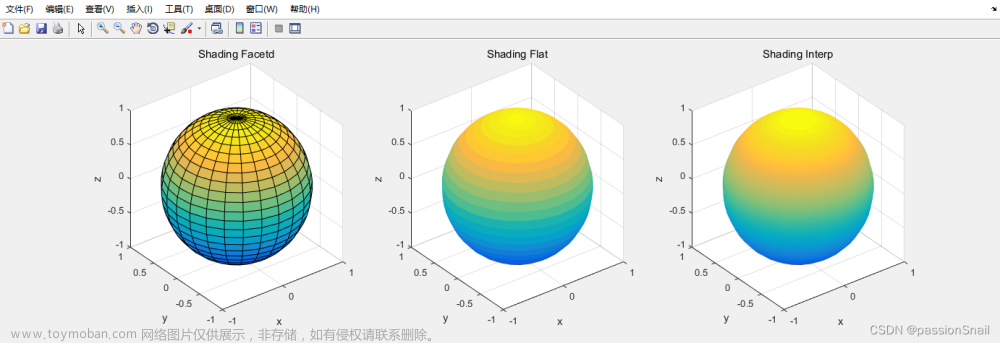
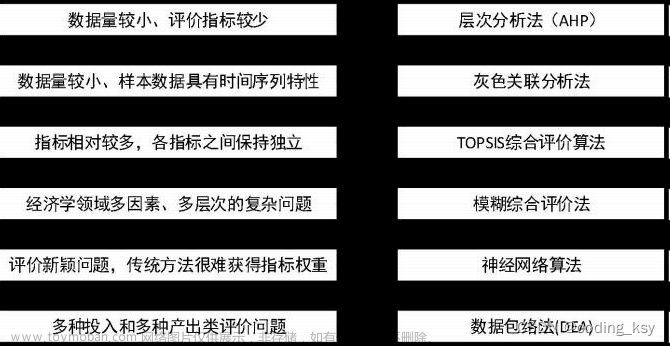
效用(Utility),是经济学中最常用的概念之一。效用:消费者拥有或消费商品或服务对欲望的满足程度被称为商品或服务的效用。一种商品或服务效用的大小取决于消费者的主观心理评价,由消费者欲望的强度所决定。 经济学家用它来解释有理性的消费者如何把他们有限的资源分配在能给他们带来最大满足的商品上。在维多利亚女王时代,哲学家和经济学家曾经轻率的将效用当做一个人整个福利指标。效用一度被认为是个人快乐的数学测度。
——百度百科
以一个简单的实物交换的例子来理解效用
甲有面包若干,乙有香肠若干。二人共进午餐时希望相互交换一部分,达到双方满意的结果。这种实物交换问题可以出现在个人之间或国家之间的各种类型的贸易市场上。显然,交换的结果取决于双方对两种物品的偏爱程度,而偏爱程度很难给出确切的定量关系,我们用作图的方法对双方将如何交换实物建立一个模型。
设交换前甲占有物品 的数量为 ,乙占有物品 的数量为 ,交换后甲占有物品 和 的数量分别为 和 。于是乙占有 和 的数量为 和 。
这样在 平面直角坐标系上,长方形 内任一点的坐标 都代表了一种交换方案(图1)。

用无差别曲线描述甲对物品 和 的偏爱程度。如果占有 数量的 和 数量的 (图1中的 点 )与占有 数量的 和 数量的 (图1中的 点),对甲来说是同样满意的话,称 和 对甲是无差别的。或者说 与 相比,甲愿意以 的减少 换取 的增加 。所有与 , 具有同样满意程度的点组成一条甲的无差别曲线 ,而比这些点的满意程度更高的点如 则位于另一条无差别曲线 上。这样,甲有无数条无差别曲线,不妨将这族曲线记作
(1)
称为满意度,随着 的增加,曲线向右上方移动。按照常识,无差别曲线应是下降的(单调递减)、下凸的(导函数单调递增或者二阶导函数大于0)和互不相交的(否则交点处则代表了一个方案有不同满意度).
同样,乙对物品 和 也有一族无差别曲线,记作
(2)
不管无差别曲线是否有解析表达式,每个人都可根据对两种物品的偏爱程度用曲线表示它们,为用图解法确定交换方案提供了依据
为得到双方满意的交换方案,将双方的无差别曲线族画在一起。图2中甲的无差别曲线族 如图1,而乙的无差别曲线族 原点在 , 轴均反向,于是当乙的满意度 增加时无差别曲线向左下移动。这两族曲线的切点连成一条曲线 ,图中用点线表示。可以断言:双方满意的交换方案应在曲线 上, 称交换路径。这是因为,假设交换在 以外的某一点 进行,若通过p’的甲的无差别曲线与 的交点为 ,甲对 和 的满意度相同,而乙对 的满意度高于 ,所以双方满意的交换不可能在 进行。
有了双方的无差别曲线,交换方案的范围可从整个长方形缩小为一条曲线 ,但仍不能确定交换究竟应在曲线 上的哪一点进行。显然,越靠近 端甲的满意度越高而乙的满意度越低,靠近 端则反之。要想把交换方案确定下来,需要双方协商或者依据双方同意的某种准则,如等价交换准则。

等价交换准则是指:两种物品用同一种货币衡量其价值,进行等价交换。不妨设交换前甲占有的 (物品 )与乙占有的 (物品 ) 具有相同的价值,, 分别相应于图3中 轴, 轴上的 两点,那么在直线 上的点进行交换,都符合等价交换准则。最后,在等价交换准则下,双方满意的交换方案必是 与 的交点 。
最后,对无差别曲线呈下凸形状作如下解释:当人们占有的 较小时( 点附近) ,他宁愿以较多的 交换较少的 (图4) ,而当占有的 较大时( 点附近),就要用较多的 换取较少的 。满足这种特性的曲线是下凸的。

“消费者追求最大效用”是经济学最优化原理中的一条
效用函数 刚打完一场篮球比赛,你又累又饿,朋友买来一袋切片面包,你狼吞虎咽地吃下一片又一片。开始的几片使饥饿感得到极大的缓解,生理上和心理上都很满足,继续吃下去,每一片面包产生的满足感逐渐减少,饱胀就不想再吃了。
为了定量研究所这吃下越来越多的面包,所得到的满足感的变化趋势,用 表示吃了 片面包后获得的满足程度,可看做面包产生的效用,如表1中吃一片面包的效用为10(单位),2片面包为20……
| 面包片数量 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 10 | 20 | 28 | 35 | 40 | 43 | 45 | 46 | 46 | 44 | ||
| 10 | 10 | 8 | 7 | 5 | 3 | 2 | 1 | 0 | |||

图1 面包的U(x)和DetU(x)图像
经济学中把像这种人们商品消费、服务消费所获得的生理和心理上的满足程度称为效用,引入效用函数 ,表示数量为 的某种商品产生的效用,用约定的某个单位来度量。为了数学研究的方便, 将 视为连续、可微函数,其变化率 表示商品数量 增加1个单位时效用函数 的增量,称为边际效用(marginal utility)。一种典型的效用函数数学表达式为
(1)
图2是(1)式中 的 和 曲线。在理性消费的情况(指消费增加效用也增加)下效用函数和边际效用具有以下性质:
1.效用函数 ,随着 的增加 递增,但增量越来越小。
2.边际效用 ,随着 的增加 递减,即边际效用的变化率为负
“边际效用递减”是经济学中一条普遍的、重要的法则。

效用函数和边际效用的特性数学表达为:
(2)
当消费者面对两种商品时效用函数会是什么样的?
无差别曲线 这次朋友买来的除了面包还有香肠,你可以搭配着吃。如果1片面包加4根香肠,或者4片面包加1根半香肠,又或者7片面包加1根香肠,都能使你获得相同的满足,那么这几种组合的效用函数的值相等。用 表示 片面包和 根香肠组合的效用函数。在图3的 平面中,上面3中组合记作 , , ,则曲线上所有的点都有 ,这条曲线称为无差别曲线(指效用相同)或等效曲线。

显然你可以画出更多的效用曲线,如图有
两种商品的效用函数 是二元函数,仍具有“边际效用递减”性质,用偏导数表示为
(3)
作为(1)式 形式的推广,一种典型的两种商品效用函数的数学表达式为
(4)
图4是(4)式中 的无差别曲线 .

数学上 是 的隐函数,即有 。如(4)式中 可表示为
(5)
无差别曲线是效用函数的几何表示。我们可以看到无差别曲线具有以下性质
(1)下降(斜率为负) 既然无差别曲线上效用函数 不变, 那么 的增加必然导致 的减少。在经济学中对于两种可以互相替代的物品, 增加1个单位引起的 的减少量称为 对 的边际替代率(绝对值): 由于偏导的性质也有:
(6)
(2)下凸(凸向原点) :即“边际替代率递减”,即
(7)

(3)互不相交 即一种组合方式不会产生多种不同效用。
效用最大化模型
如果消费者已经确定了对甲乙两种商品效用函数 和无差别曲线,那么他用一定数额的钱会购买多少数量的商品甲和乙呢?从效用最大化的角度出发,当然应该使 达到最大
设甲乙两种商品的单价分别为 消费者准备付出的钱为 ,则他购买甲乙两种商品的数量 应满足
(8)
式中 s.t为受约束于(subject to)
先从几何图形上求解这个模型,我们可以看到一簇无差别曲线和我们的约束条件形成的直线 称为消费线,当消费线与无差别线相切时,效用最大,切点 被称为消费点。

如果知道效用函数的具体表达式,我们可以按照二元函数求条件极值的方法求解。引入拉格朗日乘子 构造函数
由对 的偏导数等于0
得到
(9)
即最优解在甲乙两种商品的边际效用与二者价格之比相等时取得。记作
(10)
(10)表明了效用最大化原理 即商品的边际效用与二者价格之比相等时,效用函数最大。
这个结果与总钱数 无关,但可以给出购买甲乙两件商品的数量之比 或钱数之比
以上与几何解法结果一致。
如果效用函数为(4)则最优解有
(11)
这表明按照效用最大化原理,他购买两种商品的钱数之比,等于效用函数(4)中参数 与 之比,与商品价格无关,说明 与 分别是甲乙两种商品对消费者效用的度量,或者代表消费者对两种商品的偏爱。
模型(8)可以推广到购买 种商品的情况。记消费者的效用函数为 , 种商品的单价分别为 , 消费者准备付出的钱为 ,则他购买 种商品的数量为 。满足
(12)
用多元函数条件极值的方法求解模型为前面式子的推广文章来源:https://www.toymoban.com/news/detail-782121.html
式中边际效用与价格比值的含义是单位金额的边际效用。于是效用最大化原理又可以表示为,当每种商品单位金额的边际效用均相等时,效用函数达到最大。文章来源地址https://www.toymoban.com/news/detail-782121.html
到了这里,关于【从零开始数学建模(4)】效用函数与无差别曲线的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!