稀疏矩阵的表示以及转置-Toy模板网

这篇具有很好参考价值的文章主要介绍了稀疏矩阵的表示以及转置。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.稀疏矩阵概念

2.三元组表

3.稀疏矩阵的转置

4.题目实现

1.稀疏矩阵概念

矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵。

图示：

稀疏矩阵的转置矩阵,矩阵,线性代数,算法

文章来源地址https://www.toymoban.com/news/detail-782472.html

2.三元组表

在存储稀疏矩阵时，为了节省存储单元，很自然地想到使用压缩存储方法。但由于非零元素的分布一般是没有规律的，因此在存储非零元素的同时，还必须同时记下它所在的行和列的位置（i,j)。反之，一个三元组(i,j,aij)唯一确定了矩阵A的一个非零元。因此，稀疏矩阵可由表示非零元的三元组及其行列数唯一确定

若把稀疏矩阵中的三元组线性表按顺序储存结构储存，则称为三元组顺序表，简称为三元组表。

下图即为转化：

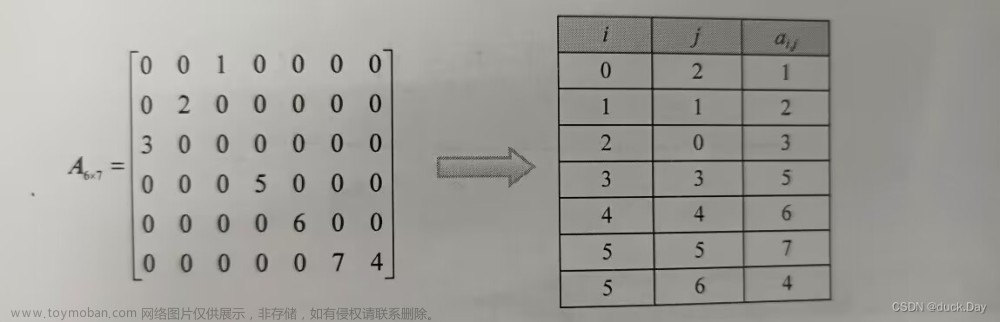
稀疏矩阵的转置矩阵,矩阵,线性代数,算法

三元组顺序表的数据类型声明如下：

#define M //稀疏矩阵行数
#define N //稀疏矩阵列数
#define MAX //稀疏矩阵中非零元最多的个数
typedef int Elem;
typedef struct 
{
	int r;//行号 
	int c;//列号 
	Elem d;//元素值 
}TupNode;

typedef struct
{
	int rows;//行数
	int cols;//列数
	int nums;//非零元素个数
	TupNode data[MAX]; 
}TSMat;

3.稀疏矩阵的转置

1.一个m×n的矩阵A，它的转置B是一个n×m的矩阵，且a[i][j]=b[j][i]，0≦i≦m，0≦j≦n，即A的行是B的列，A的列是B的行。
2. 将A转置为B，就是将A的三元组表a.data置换为表B的三元组表b.data，如果只是简单地交换a.data中i和j的内容，那么得到的b.data将是一个按列优先顺序存储的稀疏矩阵B，要得到按行优先顺序存储的b.data，就必须重新排列三元组的顺序。
由于A的列是B的行，因此，按a.data的列序转置，所得到的转置矩阵B的三元组表b.data必定是按行优先存放的
核心思想：行列互换。

解决思路：
1.将矩阵行、列维数互换；
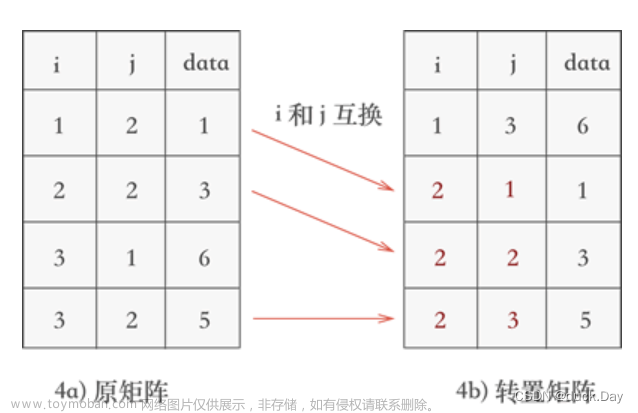
2.将每个三元组中的i和j相互调换；
3. 重排三元组次序，使B中元素以N的行(M的列)为主序。

A原矩阵三元组表 B转置后的三元组表

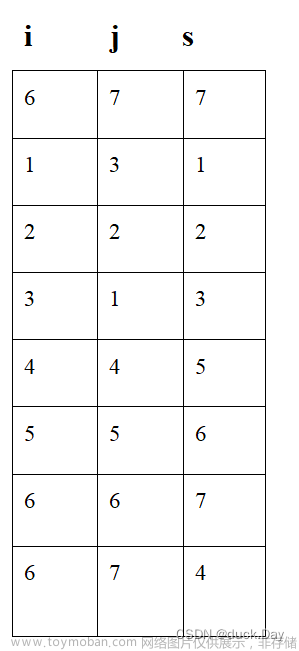
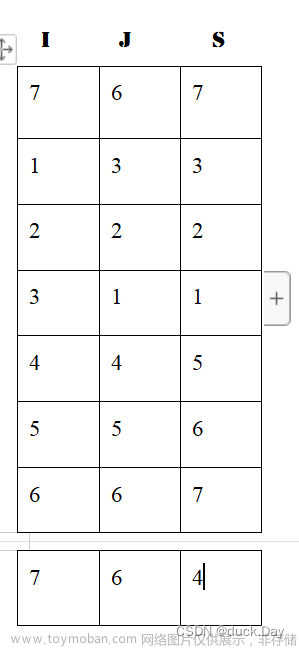
稀疏矩阵的转置矩阵,矩阵,线性代数,算法

显然发现行列互换，对A中的列又1到7循环查找，然后放入B中的行。

矩阵转置的实现思路是：不断遍历存储矩阵的三元组表，每次都取出表中 j 列最小的那一个三元组，互换行标和列标的值，并按次序存储到一个新三元组表中，。

例如，将图 2a) 三元组表存储的矩阵进行转置的过程为：

新建一个三元组表（用于存储转置矩阵），并将原矩阵的行数和列数互换赋值给新三元组；
遍历三元组表，找到表中 j 列最小值 1 所在的三元组 (3,1,6)，然后将其行标和列标互换后添加到一个新的三元组表中，如图 3所示：

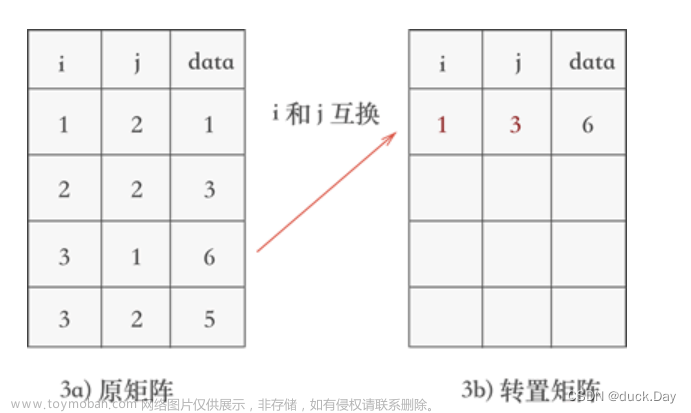
3.继续遍历三元组表，找到表中 j 列次小值为 2 的三元组，分别为 (1,2,1)、(2,2,3) 和 (3,2,5)，根据找到它们的先后次序将各自的行标和列标互换后添加到新三元组表中，如图所示：

稀疏矩阵的转置矩阵,矩阵,线性代数,算法

代码实现：

void TranMat(TSMat *t,TSMat *tb)//t为A的三元组顺序表，tb为B的三元组顺序表
{
	int k,k1=0,v;                       //k1记录tb中元素个数
	tb->rows=t->cols;tb->cols=t->rows;  //行列互换
    tb->nums=t->nums;
	if(t->nums!=0)                      //当存在非零元时进行转置
	{
		for(v=0;v<t->cols;v++)          //按v=0.1....t.cols循环
		{
			for(k=0;k<t->nums;k++)      //k用于扫描t.data的所有元素
			{
				if(t->data[i].c==v)    //找到一个列号为v的元素
				{
					tb->data[k1].r=t->data[k].c;   //tb的行为t的列
					tb->data[k1].c=t->data[k].r;   //tb的列为t的行
					tb->data[k1].d=t->data[k].d;   //值不变
					k1++;                           //tb中元素的个数增加1.
				}
			}
		}

4.题目实现

把给定的二维稀疏矩阵用三元组表表示和存储，并进行稀疏矩阵的转置，输出转置后的稀疏矩阵的三元组表。

假如给定如下二维稀疏矩阵：

3 0 0 1 0 0

0 4 0 0 0 0

5 0 0 2 0 0

代码实现：

#include<stdio.h>
#define M 3
#define N 6
#define MAX 20
typedef int Elem;
typedef struct 
{
	int H;//行号 
	int L;//列号 
	Elem d;//元素值 
}TupNode;

typedef struct
{
	int rows;//行数
	int cols;//列数
	int nums;//非零元素个数
	TupNode data[MAX]; 
}TSMat;

void CreatMat(TSMat *B,Elem A[M][N])
{
	int i,j;
	B->rows =M;B->cols =N;B->nums =0 ;
	for(i=0;i<M;i++)
	{
		for(j=0;j<N;j++)
		{
			if(A[i][j]!=0)
			{
				B->data[B->nums].H=i;
				B->data[B->nums].L=j;
				B->data[B->nums].d=A[i][j];
				B->nums++;
			}
		}
	}
}//把二维稀疏矩阵用三元组表表示

void Print(TSMat *B)
{
	int i;
	if(B->nums<=0)
	{
		return ;
	}
	printf("%d   %d   %d\n",B->rows,B->cols,B->nums);
	printf("---------\n");
	for(i=0;i<B->nums;i++)
	{
		printf("%d   %d   %d\n",B->data[i].H,B->data[i].L,B->data[i].d);
	}
}//三元组表的输出 

void TranMat(TSMat *B,TSMat *b)
{
	int i,j=0,k;
	b->rows=B->cols;b->cols=B->rows;b->nums=B->nums;
	if(B->nums!=0)
	{
		for(k=0;k<B->cols;k++)
		{
			for(i=0;i<B->nums;i++)
			{
				if(B->data[i].L==k)
				{
					b->data[j].H=B->data[i].L;
					b->data[j].L=B->data[i].H;
					b->data[j].d=B->data[i].d;
					j++;
				}
			}
		}
	}
} //稀疏矩阵的转置 

int main()
{
	TSMat B,b;
	int i,j;
	int A[M][N]={{3,0,0,1,0,0},{0,4,0,0,0,0},{5,0,0,2,0,0}};//这里可以可以自己用两个循环语句进行输入
	printf("原来的二维稀疏矩阵为:\n");
	for(i=0;i<M;i++)
	{
		for(j=0;j<N;j++)
		{
			printf("%d  ",A[i][j]);
		}
		printf("\n");
	}
	printf("二维稀疏矩阵用三元组表表示为:\n");
	CreatMat(&B,A);
	Print(&B);
	printf("稀疏矩阵三元组表的转置为:\n");
	TranMat(&B,&b);
	Print(&b);
	return 0;
}

运行结果图片：

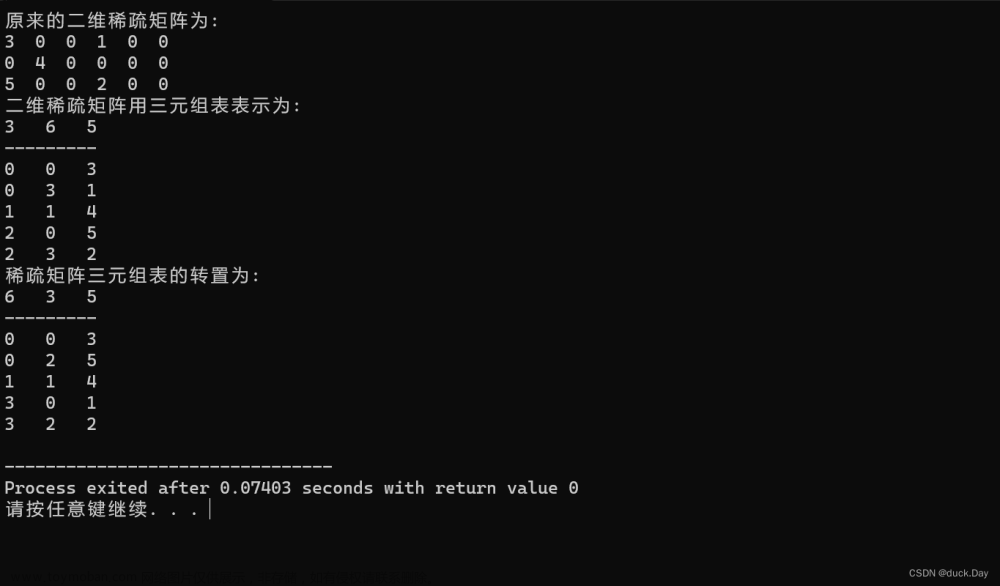
稀疏矩阵的转置矩阵,矩阵,线性代数,算法