【排序】归并排序（C语言实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【排序】归并排序（C语言实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 递归版的归并排序

1.1 归并排序的思想

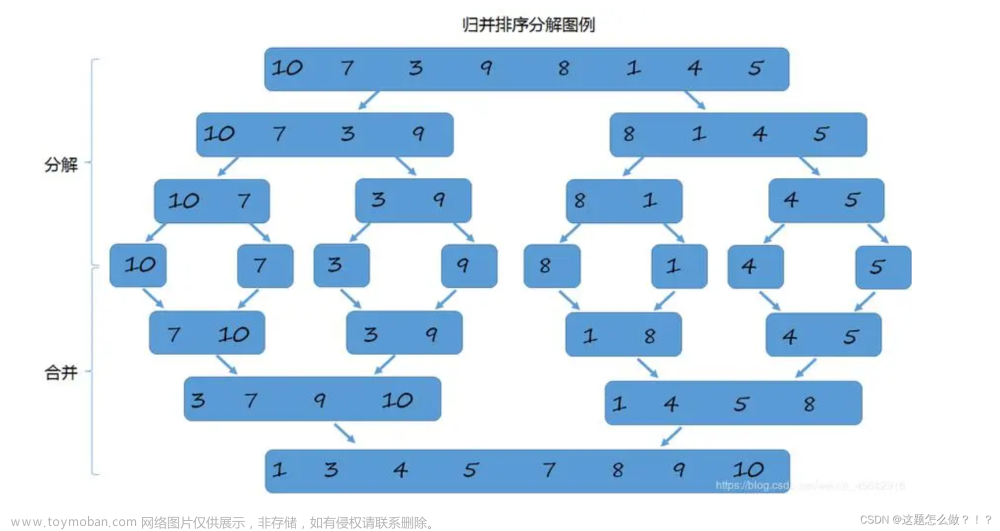
归并排序（MERGE - SORT）是建立在归并操作上的一种有效的排序算法, 该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序核心步骤：
【排序】归并排序（C语言实现）,c语言,算法,排序算法

这里我们先介绍一下递归版本的归并排序的思想：

我们需要先创建一个临时数组，用来将需要排序的数组归并到这个临时数组里面去，然后再将这个数组拷贝到原数组中去，这样就完成了排序的过程。

2. 递归版的归并排序的实现

具体实现方式如下：

void Sub_MergeSort(int* a, int* tmp, int begin, int end)
{
	if (begin >= end - 1) // 我控制的是左闭右开区间
		return;

	int key = (begin + end) / 2;
	// [left,key + 1) [key,end) 左闭右开的空间一定要控制好
	int begin1 = begin, end1 = key;
	int begin2 = key, end2 = end;
	
	Sub_MergeSort(a, tmp, begin1, end1);
	Sub_MergeSort(a, tmp, begin2, end2);

	// 归并过程
	int indix = begin;
	while (begin1 < end1 && begin2 < end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[indix++] = a[begin1++];
		}
		else
		{
			tmp[indix++] = a[begin2++];
		}
	}
	while (begin1 < end1)
	{
		tmp[indix++] = a[begin1++];
	}
	while (begin2 < end2)
	{
		tmp[indix++] = a[begin2++];
	}

	// 将tmp数组中的元素拷贝到元素中
	memmove(a + begin, tmp + begin, (end - begin)*sizeof(int));
}


void MergeSort(int* a, int n)
{
	
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail\n");
		return;
	}
	// 因为这里开一次空间就够用了,所以递归过程我们还是要写成一个子函数来完成
	Sub_MergeSort(a, tmp, 0, n);

	free(tmp);
	tmp = NULL;
}

2. 非递归版的归并排序

所以在平时我们要使用归并排序时，使用递归版的完全够用了。但由于现在还在学习阶段，所以掌握一下非递归版的归并排序还是有必要的。

把递归改成非递归，这个怎么处理呢？可以像我们之前讲的快速排序的非递归一样使用栈吗？

这里实现非递归的归并排序使用栈其实不是很好的方式，反而会使问题变复杂。

【排序】归并排序（C语言实现）,c语言,算法,排序算法
所以我们就得想其他办法：

可以这样：
【排序】归并排序（C语言实现）,c语言,算法,排序算法
但是这里需要注意两种情况：

这里不控制好边界的话，很容易就造成越界了，这里我分享两种控制边界的方式，细节我写在注释里了：

方式一：

// 归并排序 -- 非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail\n");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0;i < n;i = 2 * gap + i)
		{
			int begin1 = i, end1 = i + gap - 1; // 定义每次归并时的第一组数据
			int begin2 = i + gap, end2 = i + 2 * gap - 1; // 定义每次归并时的第二组数据

			if (begin2 >= n) // 如果第二组不存在了,这一趟就不用归并了
			{
				break;
			}

			if (end2 >= n) // 如果存在第二组,但第二组的末尾越界了,应该调整一下
			{
				end2 = n - 1;
			}

			// 归并过程
			int indix = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[indix++] = a[begin1++];
				}
				else
				{
					tmp[indix++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[indix++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[indix++] = a[begin2++];
			}

			// 将tmp数组拷贝回原数组
			memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
		}
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}

方式二：文章来源地址https://www.toymoban.com/news/detail-782627.html

void MergeSortNonR2(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail\n");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		int j = 0;
		for (int i = 0;i < n;i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			// end1 >= n - 1 和begin2 >= n 都代表没有第二组,所以第二组就不用参与归并过程
			if (end1 >= n)
			{
				end1 = n - 1;

				// 此时begin2和end2一定是越界的
				// 我们手动让这段空间不存在
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				// 我们手动让这段空间不存在
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n) // 此时end1 和 begin2都没有越界
			{
				end2 = n - 1;
			}

			// 归并过程
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}
		memcpy(a, tmp, sizeof(int) * n);
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}