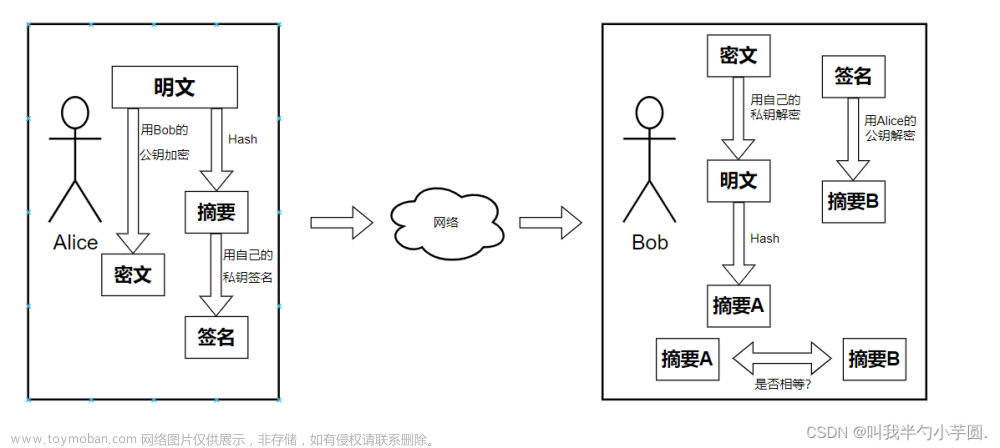
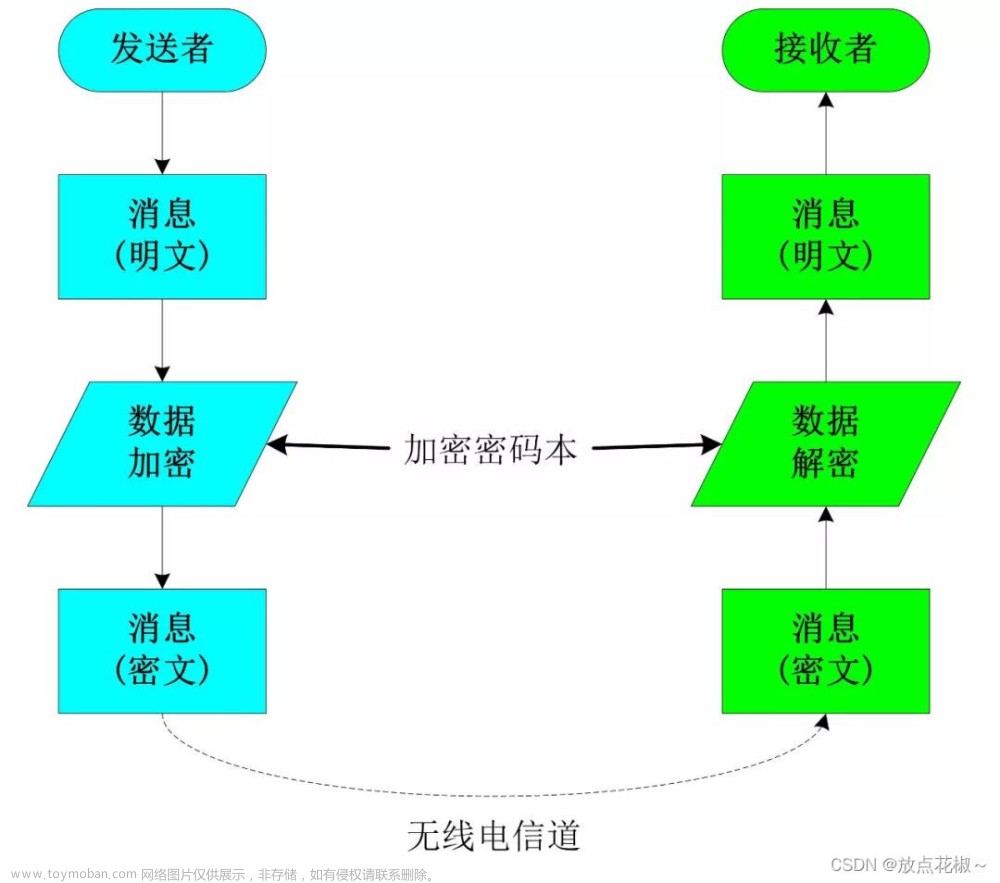
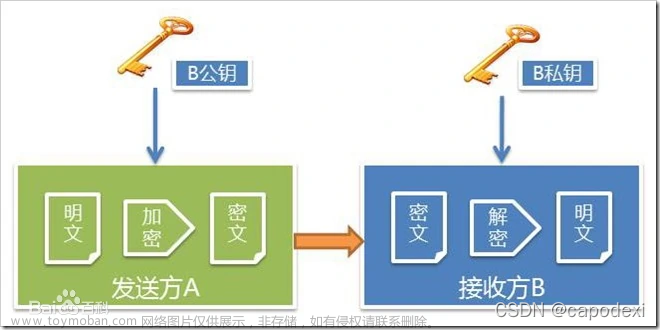
本文主要解决古典密码中的Hill体制密码在已知明文M和密文C的情况下求解密钥矩阵K的两种方法:①求逆矩阵②待定系数法。
如若不懂Hill体制的古典密码可以参照我上一篇文章密码学——几种典型的古典密码体制(Caesar体制、Playfair体制、Vigenere体制、Beaufort体制以及Hill体制)
引入题目
设英文字母A,B,C,…,Z分别对应编码为0,1,2,…,25。已知Hill密码中的明文长度为2,密钥K为 Z 26 Z_{26} Z26上的一个二阶可逆方阵,现给出明文FRID,所对应的密文为PQCF,试求解密钥矩阵K
一、求解逆矩阵
此处只是简单的描述线性代数中求解逆矩阵的步骤
设矩阵
M
=
(
5
17
8
3
)
M=\begin {pmatrix}5 & 17 \\ 8 &3 \end{pmatrix} \\
M=(58173)
解:①
∣
M
∣
=
5
×
3
−
8
×
17
=
−
121
=
9
(
m
o
d
26
)
\vert M \vert =5\times3-8\times17=-121=9\ (mod\ 26)
∣M∣=5×3−8×17=−121=9 (mod 26)注意,在模运算中-121模26等同于9模26
∣
M
∣
−
1
=
3
(
m
o
d
26
)
∵
3
×
9
=
27
≡
1
(
m
o
d
26
)
\vert M \vert^{-1} =3\ (mod\ 26) \because 3\times 9=27\equiv1\ (mod\ 26)
∣M∣−1=3 (mod 26)∵3×9=27≡1 (mod 26)注意,在模运算中逆元的求解为相乘模26余1
②
M
∗
=
(
3
−
17
−
8
5
)
M^*=\begin {pmatrix}3 & -17 \\ -8 &5 \end{pmatrix} \\
M∗=(3−8−175)注意,此处的
M
∗
M^*
M∗表示的是M的代数余子式,如若不知如何求代数余子式可以去搜查有关知识,此处有个方便的小tips:主对角线交换位置,副对角线变为负(仅限2x2矩阵的代数余子式)
③
M
−
1
=
∣
M
∣
−
1
⋅
M
∗
=
3
⋅
(
3
−
17
−
8
5
)
=
(
9
1
2
15
)
M^{-1}=\vert M \vert^{-1} \cdot M^*=3\cdot \begin {pmatrix}3 & -17 \\ -8 &5 \end{pmatrix} =\begin {pmatrix}9 & 1 \\ 2 &15 \end{pmatrix} \\
M−1=∣M∣−1⋅M∗=3⋅(3−8−175)=(92115)注意,此处都是进行了模26的操作,所以结果都为正数
二、求解方法
1.逆矩阵求解法
解:
①因为明文分组长度为2,所以明文、密文向量每一组的列数为2。
明文
∵
F
→
5
,
R
→
17
,
I
→
8
,
D
→
3
\because F\to 5,R \to 17,I\to 8,D\to 3
∵F→5,R→17,I→8,D→3密文
P
→
15
,
Q
→
16
,
C
→
2
,
F
→
5
P\to 15,Q \to 16,C\to 2,F\to 5
P→15,Q→16,C→2,F→5注意,此处的数字是字母对应
Z
26
Z_{26}
Z26上的数字
所以明文向量(5,17)(8,3)密文向量(15,16)(2,5)
∵
c
=
m
K
m
o
d
26
\because c=mK\ mod\ 26
∵c=mK mod 26
∴
(
15
,
16
)
=
(
5
,
17
)
K
,
(
2
,
5
)
=
(
8
,
3
)
K
\therefore (15,16)=(5,17)K,(2,5)=(8,3)K
∴(15,16)=(5,17)K,(2,5)=(8,3)K
故
(
15
16
2
5
)
=
(
5
17
8
3
)
K
\begin {pmatrix}15 & 16 \\ 2 &5 \end{pmatrix} = \begin {pmatrix}5 & 17 \\ 8 &3\end{pmatrix} K
(152165)=(58173)K注意,整合为一个矩阵的时候一定要行向量对应
由
c
=
m
K
m
o
d
26
c=mK\ mod\ 26
c=mK mod 26,得
m
−
1
c
=
m
−
1
m
K
=
K
m^{-1}c=m^{-1}mK=K
m−1c=m−1mK=K 注意,某数和其逆元相乘的结果是单位E,也就是1
②求解明文的逆矩阵如前面一、求解逆矩阵所示,此处不赘述。
③带入逆矩阵求得结果
K
=
m
−
1
c
=
(
9
1
2
15
)
(
15
16
2
5
)
=
(
9
×
15
+
1
×
2
9
×
16
+
1
×
5
2
×
15
+
15
×
2
2
×
16
+
15
×
5
)
=
(
137
149
60
107
)
=
(
7
19
8
3
)
m
o
d
26
K=m^{-1}c\\= \begin {pmatrix}9 & 1 \\ 2 &15 \end{pmatrix} \begin {pmatrix}15 & 16 \\ 2 &5\end{pmatrix} \\= \begin {pmatrix}9\times15+1\times2 & 9\times16+1\times5\\ 2\times15+15\times2 &2\times16+15\times5\end{pmatrix}\\=\begin {pmatrix}137 & 149 \\ 60 &107 \end{pmatrix} \\=\begin {pmatrix}7 & 19 \\ 8 &3 \end{pmatrix}\ mod\ 26
K=m−1c=(92115)(152165)=(9×15+1×22×15+15×29×16+1×52×16+15×5)=(13760149107)=(78193) mod 26
故密钥K为
(
7
19
8
3
)
\begin {pmatrix}7 & 19 \\ 8 &3 \end{pmatrix}
(78193)
2.待定系数求解法
解:
设密钥矩阵K为
(
k
11
k
12
k
21
k
22
)
\begin {pmatrix}k_{11} & k_{12} \\ k_{21} &k_{22} \end{pmatrix}
(k11k21k12k22),根据
(
15
16
2
5
)
=
(
5
17
8
3
)
(
k
11
k
12
k
21
k
22
)
\begin {pmatrix}15 & 16 \\ 2 &5 \end{pmatrix} = \begin {pmatrix}5 & 17 \\ 8 &3\end{pmatrix} \begin {pmatrix}k_{11} & k_{12} \\ k_{21} &k_{22} \end{pmatrix}
(152165)=(58173)(k11k21k12k22)得
{
5
k
11
+
17
k
21
≡
15
m
o
d
26
5
k
12
+
17
k
22
≡
16
m
o
d
26
8
k
11
+
3
k
21
≡
2
m
o
d
26
8
k
12
+
3
k
22
≡
5
m
o
d
26
⇒
{
40
k
11
+
136
k
21
≡
120
m
o
d
26
①
40
k
11
+
15
k
21
≡
10
m
o
d
26
②
40
k
12
+
136
k
22
≡
128
m
o
d
26
③
40
k
12
+
15
k
22
≡
25
m
o
d
26
④
\begin{cases} 5k_{11}+17k_{21}\equiv15\ mod\ 26\\ 5k_{12}+17k_{22}\equiv16\ mod\ 26\\ 8k_{11}+3k_{21}\equiv2\ mod\ 26\\ 8k_{12}+3k_{22}\equiv5\ mod\ 26 \end{cases} \Rightarrow \begin{cases} 40k_{11}+136k_{21}\equiv120\ mod\ 26\ ①\\ 40k_{11}+15k_{21}\equiv10\ mod\ 26\ ②\\ 40k_{12}+136k_{22}\equiv128\ mod\ 26\ ③\\ 40k_{12}+15k_{22}\equiv25\ mod\ 26\ ④ \end{cases}
⎩
⎨
⎧5k11+17k21≡15 mod 265k12+17k22≡16 mod 268k11+3k21≡2 mod 268k12+3k22≡5 mod 26⇒⎩
⎨
⎧40k11+136k21≡120 mod 26 ①40k11+15k21≡10 mod 26 ②40k12+136k22≡128 mod 26 ③40k12+15k22≡25 mod 26 ④
①
−
②
,
③
−
④
⇒
{
121
k
21
≡
110
m
o
d
26
121
k
22
≡
103
m
o
d
26
①-②,③-④\Rightarrow \begin{cases} 121k_{21}\equiv110\ mod26\\ 121k_{22}\equiv103\ mod26\\ \end{cases}
①−②,③−④⇒{121k21≡110 mod26121k22≡103 mod26
⇒
{
17
k
21
≡
6
m
o
d
26
17
k
22
≡
25
m
o
d
26
⇒
{
k
21
≡
23
×
6
≡
8
m
o
d
26
k
22
≡
23
×
25
≡
3
m
o
d
26
\Rightarrow \begin{cases} 17k_{21}\equiv6\ mod26\\ 17k_{22}\equiv25\ mod26\\ \end{cases} \Rightarrow \begin{cases} k_{21}\equiv23\times6\equiv8\ mod26\\ k_{22}\equiv23\times25\equiv3\ mod26\end{cases}
⇒{17k21≡6 mod2617k22≡25 mod26⇒{k21≡23×6≡8 mod26k22≡23×25≡3 mod26
故带入
k
21
,
k
22
k_{21},k_{22}
k21,k22的值可得
{
5
k
11
+
17
×
8
≡
15
m
o
d
26
5
k
12
+
17
×
3
≡
16
m
o
d
26
⇒
{
k
11
≡
7
m
o
d
26
k
12
≡
19
m
o
d
26
\begin{cases} 5k_{11}+17\times8\equiv15\ mod26\\ 5k_{12}+17\times3\equiv16\ mod26\\ \end{cases} \Rightarrow \begin{cases} k_{11}\equiv7\ mod26\\ k_{12}\equiv19\ mod26\end{cases}
{5k11+17×8≡15 mod265k12+17×3≡16 mod26⇒{k11≡7 mod26k12≡19 mod26
故密钥K为
(
7
19
8
3
)
\begin {pmatrix}7 & 19 \\ 8 &3 \end{pmatrix}
(78193)文章来源:https://www.toymoban.com/news/detail-782716.html
结束语
以上就是有关密码学的Hill体制有关已知明文和密文如何求解密钥矩阵的两种方法的介绍,希望能对读者们起到一定的作用。
如果存在错误欢迎在评论区指出,可以多多交流,大家一起进步。文章来源地址https://www.toymoban.com/news/detail-782716.html
到了这里,关于密码学——Hill体制密码中已知明文M和密文C求解密钥矩阵K的两种方法之逆矩阵求解法和待定系数求解法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!