1. Toy模板网首页
  2. > Toy博客

深度优先搜索（DFS）和广度优先搜索（BFS）

10月前 作者：daoboker 分类：Toy博客 阅读(55) 违法举报

这篇具有很好参考价值的文章主要介绍了深度优先搜索（DFS）和广度优先搜索（BFS）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

代码随想录
深度优先搜索和广度优先搜索，都是图形搜索算法，它两相似，又却不同，在应用上也被用到不同的地方。这里拿一起讨论，方便比较。
先给大家说一下两者大概的区别：

  1. 如果搜索是以接近起始状态的程序依次扩展状态的，叫广度优先搜索。
    如果扩展是首先扩展新产生的状态，则叫深度优先搜索。
    深度优先搜索：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。
    广度优先搜索：又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。

  2. 二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

  3. 通常深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。 　
    广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些。

一、深度优先搜索

深度优先搜索属于图算法的一种，是一个针对图和树的遍历算法，英文缩写为DFS即Depth First Search。深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。一般用栈stack数据结构来辅助实现DFS算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。
若将bfs策略应用于树结构，其效果等同与前中后序遍历。

1.1 基本步骤

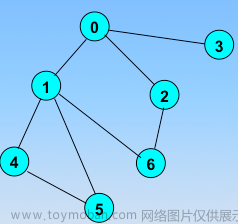
  1. 对于下面的树而言，DFS方法首先从根节点1开始，其搜索节点顺序是1,2,3,4,5,6,7,8（假定左分枝和右分枝中优先选择左分枝）。
    深度优先搜索和广度优先搜索对比,深度优先,宽度优先
  2. 从stack中访问栈顶的点；
    深度优先搜索和广度优先搜索对比,深度优先,宽度优先
  3. 找出与此点邻接的且尚未遍历的点，进行标记，然后放入stack中，依次进行；
    深度优先搜索和广度优先搜索对比,深度优先,宽度优先
  4. 如果此点没有尚未遍历的邻接点，则将此点从stack中弹出，再按照（3）依次进行；
    深度优先搜索和广度优先搜索对比,深度优先,宽度优先深度优先搜索和广度优先搜索对比,深度优先,宽度优先
  5. 直到遍历完整个树，stack里的元素都将弹出，最后栈为空，DFS遍历完成。
    深度优先搜索和广度优先搜索对比,深度优先,宽度优先

1.2 代码模板

  1. 确认递归函数，参数
    首先我们dfs函数一定要存一个图，用来遍历的，还要存一个目前我们遍历的节点，定义为x。至于单一路径，和路径集合可以放在全局变量，那么代码是这样的：
vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 0节点到终点的路径
// x：目前遍历的节点
// graph：存当前的图
void dfs (vector<vector<int>>& graph, int x)
  1. 确认终止条件
    什么时候我们就找到一条路径了？
    当目前遍历的节点 为 最后一个节点的时候，就找到了一条，从 出发点到终止点的路径。
    当前遍历的节点，我们定义为x，最后一点节点，就是 graph.size() - 1。
    所以 但 x 等于 graph.size() - 1 的时候就找到一条有效路径。 代码如下：
// 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.size() - 1
if (x == graph.size() - 1) { // 找到符合条件的一条路径
    result.push_back(path); // 收集有效路径
    return;
}
  1. 处理目前搜索节点出发的路径
    接下来是走 当前遍历节点x的下一个节点。
    首先是要找到 x节点链接了哪些节点呢？ 遍历方式是这样的：
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点

接下来就是将 选中的x所连接的节点，加入到 单一路径来。

path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
  1. 当前遍历的节点就是 graph[x][i] 了，所以进入下一层递归
dfs(graph, graph[x][i]); // 进入下一层递归
  1. 最后就是回溯的过程，撤销本次添加节点的操作。 该过程代码：
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
    path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
    dfs(graph, graph[x][i]); // 进入下一层递归
    path.pop_back(); // 回溯，撤销本节点
}
  1. 整体代码
// 深度优先搜索 C++代码模板
class Solution {
private:
    vector<vector<int>> result; // 收集符合条件的路径
    vector<int> path; // 0节点到终点的路径
    // x：目前遍历的节点
    // graph：存当前的图
    void dfs (vector<vector<int>>& graph, int x, vector<bool>& used) {
        // 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.size() - 1
        if (x == graph.size() - 1) { // 找到符合条件的一条路径
            result.push_back(path);
            return;
        }
        unordered_set<int> visited; // 定义set对同一节点下的本层去重
        for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
        	// 要对同一树层使用过的元素进行跳过
        	if (visited.find(graph[x][i]) != visited.end()) { // 如果发现出现过就pass
                continue;
            }
            visited.insert(graph[x][i]);	//set跟新元素
            path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
            dfs(graph, graph[x][i]); // 进入下一层递归
            path.pop_back(); // 回溯，撤销本节点
        }
    }
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        path.push_back(0); // 无论什么路径已经是从0节点出发
        dfs(graph, 0); // 开始遍历
        return result;
    }
};

二、广度优先搜索

广度优先搜索（也称宽度优先搜索，缩写BFS即即Breadth First Search）是连通图的一种遍历算法。这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和广度优先搜索类似的思想。其属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。基本过程，BFS是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。

所采用的策略可概况为越早被访问到的顶点，其邻居顶点越早被访问。于是，从根顶点s的BFS搜索，将首先访问顶点s；再依次访问s所有尚未访问到的邻居；再按后者被访问的先后次序，逐个访问它们的邻居。一般用队列queue数据结构来辅助实现BFS算法。
若将bfs策略应用于树结构，其效果等同与层次遍历。

2.1 基本步骤

仿照树的层次遍历，借助队列来存储已访问过得顶点。
过程：先从图中选取一个顶点，作为遍历图的起始顶点，并加入队列中，然后依次访问该顶点的邻居顶点，并按照顺序加入队列中。 当访问了该顶点的所有邻居顶点后，把该顶点从队列中移除。接着获取新的队列头，访问该顶点的邻居顶点，最后以此类推，直到所有顶点被访问。
在遍历时，该顶点的邻居顶点有可能已经被访问过了，意味着边不属于遍历树，可将该边归类为跨边(cross edge)

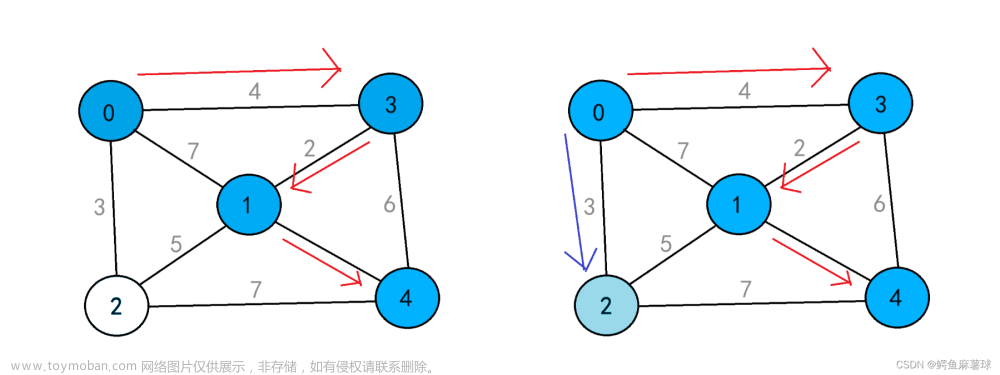
下图给出一个8个顶点，11条边的有向图的BFS，始于顶点s
深度优先搜索和广度优先搜索对比,深度优先,宽度优先

2.2 代码模板

void bfs() {
	if(root==nullptr) return;
	queue<TreeNode*> que;
	queue.push(root);
	unordered_set<int> visited; // 记录遍历过的节点
	vector<vector<int>> result;
	//开始遍历队列
    while (!que.empty()) {
         int size = que.size();
         vector<int> vec;
         // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
         for (int i = 0; i < size; i++) {
             TreeNode* node = que.front();
             que.pop();
             if (visited.find(node) != visited.end()) { // 如果发现出现过就pass
                continue;
             }
             visited.insert(node);	//set跟新元素
             vec.push_back(node->val);
             if (node->left) que.push(node->left);
             if (node->right) que.push(node->right);
         }
         result.push_back(vec);
     }
}

三、例题

岛屿的最大面积
深度优先搜索和广度优先搜索对比,深度优先,宽度优先

3.1 深搜+递归

class Solution {
public:
    // DFS 用递归实现
    int dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int i, int j) {
        // 终止条件
        if(i<0 || j<0 || i>=grid.size() || j>=grid[0].size() || grid[i][j]==0 || visited[i][j]==true)
            return 0;

        visited[i][j]=true; // true为已遍历过
        int area = 1;
        vector<vector<int>> directions = {{1,0},{0,1},{-1,0},{0,-1}};
        for(auto dir : directions) {
            int next_i = i + dir[0];
            int next_j = j + dir[1];
            area += dfs(grid, visited, next_i, next_j);
        }
        return area;
    }

    int maxAreaOfIsland(vector<vector<int>>& grid) {
        vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size(), false)); //初始化全为false没被遍历过
        int maxArea = 0;
        for(int i=0; i<grid.size(); i++) {
            for(int j=0; j<grid[0].size(); j++) {
                if(grid[i][j]==1 && visited[i][j]==false)
                    maxArea = max(maxArea, dfs(grid, visited, i, j));
            }
        }
        return maxArea;
    }
};

3.2 广搜+迭代

class Solution {
public:
    // BFS 用迭代实现
    int dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int i, int j) {
        queue<pair<int, int>> que;
        que.push({i, j});
        visited[i][j]=true; // true为已遍历过

        int area = 0;
        while(!que.empty()) {
            auto pos = que.front();
            que.pop();
            area++;

            vector<vector<int>> directions = {{1,0},{0,1},{-1,0},{0,-1}};
            for(auto dir : directions) {
                int next_i = pos.first + dir[0];
                int next_j = pos.second + dir[1];
                if(next_i>=0 && next_i<grid.size() && next_j>=0 && next_j<grid[0].size() && grid[next_i][next_j]==1 && visited[next_i][next_j]==false) {
                    que.push({next_i, next_j});
                    visited[next_i][next_j] = true;
                }                   
            }
        }
        return area;
    }
        

    int maxAreaOfIsland(vector<vector<int>>& grid) {
        vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size(), false)); //初始化全为false没被遍历过
        int maxArea = 0;
        for(int i=0; i<grid.size(); i++) {
            for(int j=0; j<grid[0].size(); j++) {
                if(grid[i][j]==1 && visited[i][j]==false)
                    maxArea = max(maxArea, dfs(grid, visited, i, j));
            }
        }
        return maxArea;
    }
};

3.3 深搜+迭代

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int ans = 0;
        for (int i = 0; i != grid.size(); ++i) {
            for (int j = 0; j != grid[0].size(); ++j) {
                int cur = 0;
                stack<int> stacki;
                stack<int> stackj;
                stacki.push(i);
                stackj.push(j);
                while (!stacki.empty()) {
                    int cur_i = stacki.top(), cur_j = stackj.top();
                    stacki.pop();
                    stackj.pop();
                    if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {
                        continue;
                    }
                    ++cur;
                    grid[cur_i][cur_j] = 0;
                    int di[4] = {0, 0, 1, -1};
                    int dj[4] = {1, -1, 0, 0};
                    for (int index = 0; index != 4; ++index) {
                        int next_i = cur_i + di[index], next_j = cur_j + dj[index];
                        stacki.push(next_i);
                        stackj.push(next_j);
                    }
                }
                ans = max(ans, cur);
            }
        }
        return ans;
    }
};

3.4 哇为机试题

华为机试题非常喜欢出Dfs题，都不是原题，23届校招机试好多疫情下餐厅坐座位之类的题。
例 - 题目：士兵的任务2
士兵在迷宫中执行任务，迷宫中危机重重，他需要在在最短的时间内到达指定的位置。你可以告诉士兵他最少需要多长时间吗?的迷宫中，迷宫中0为路，1为墙，2为起点，3为终点，输入一个4为陷阱，6为炸弹。士兵只能向上下左右四个方向移动，如果路径上为墙，不能移动。已知每走一步需要花费1个单位的时间，走到陷阱上需要花费3个单位的时间，走到炸弹上将会激活炸弹将炸弹上下左右的墙炸为路。
注意点：
1、炸弹只能炸毁墙，不会炸掉陷阱
2、炸弹、陷阱只能发挥一次作用
3、迷宫为最人为25
4、用例保证士兵一定有方法能到达终点
解答要求
时间限制: C/C++ 6000ms.其他语言: 12000ms内存限制: C/C++256MB，其他语言: 512MB
输出
最少需要的单位时间

样例1

输入:
44
1111
1101
1311
输出: 3
解释:士兵在位置2，向左移动到炸弹上，会将炸弹周围的墙炸掉，向下走两步即可到达终点
样例2
输入:8 416211101110111011101110111011131
输出:7
解释:士兵在位置2，向下移动7步即可到达终点

#include<iostream>
#include<vector>
#include<queue>
using namespace std;

vector<int> direction_x = {-1, 1, 0, 0};
vector<int> direction_y = {0, 0, -1, 1};

int cnt = INT32_MAX;
int m, n;
void dfs(int x, int y, vector<vector<int>>& grid, vector<vector<int>>& visited, int step) {
	if(grid[x][y] == 3) {	//抵达终点
		cnt = min(cnt, step + 1);
		return;
	}
	if (grid[x][y] == 1)	//遇到墙
		return;
	if (grid[x][y] == 6) {	//遇到炸弹
		queue<vector<int>> boom;
		boom.push({x, y});
		vector<vector<int>> tmp = grid;	//炸弹会改变地图，创建临时地图，用于回溯
		tmp[x][y] = 0;
		//炸弹用BFS做，炸开素有炸弹和墙
		while (!boom.empty()) {
			for (int i=0; i<4; i++) {
				int boomx = boom.front()[0] + direction_x[i], boomy = boom.front()[1] + direction_y[i];
				if (boomx >= 0 && boomx < m && boomy >= 0 && boomy < n) {
					if (tmp[boomx][boomy] == 1)
						tmp[boomx][boomy] = 0;	//墙炸为路
					if (tmp[boomx][boomy] == 6)	{	//新的炸弹需要添加之后重新炸
						tmp[boomx][boomy] = 0;
						boom.push({boomx, boomy});
					}
				}
			}
			boom.pop();
		}
		dfs(x, y, tmp, visited, step);	//炸完后地图改变用新地图继续深搜
	}
	if (grid[x][y] == 0)	{	//遇到路
		visited[x][y] = 1;
		for (int i = 0; i < 4; ++i) {
			int newx = x + direction_x[i], newy = y + direction_y[i];
			if (newx < 0 || newx >= m || newy < 0 || newy >= n || visited[newx][newy])
				continue;
			dfs(newx, newy, grid, visited, step + 1);
		}
		visited[x][y] = 0;
	}
	if (grid[x][y] == 4) {	//遇到陷阱
		visited[x][y] = 1;
		for (int i = 0; i < 4; ++i) {
			int newx = x + direction_x[i], newy = y + direction_y[i];
			if (newx < 0 || newx >= m || newy < 0 || newy >= n || visited[newx][newy])
				continue;
			dfs(newx, newy, grid, visited, step + 3);
		}
		visited[x][y] = 0;
	}
	if (grid[x][y] == 2) {	//起点
		visited[x][y] = 1;
		for(int i = 0; i < 4; ++i) {
			int newx = x + direction_x[i], newy = y + direction_y[i];
			if (newx < 0 || newx >= m || newy < 0 || newy >= n || visited[newx][newy])
				continue;
			dfs(newx, newy, grid, visited, step);
		}
	}
}

int main() {
	int start_x, start_y;
	cin >> m >> n;
	vector<vector<int>> grid(m, vector<int>(n));
	vector<vector<int>> visited(m, vector<int>(n));
	for (int i = 0; i < m; ++i)
		for (int j = 0; j < n; ++j)	{
			cin >> grid[i][j];
			if (grid[i][j] == 2)
				start_x = i, start_y = j;
		}
	dfs(start_x, start_y, grid, visited, 0);
	cout << cnt << endl;
	/*backtrack(1, 2, grid, visited, 0);
	/*vector<vector<int>> steps(m, vector<int>(n, -1));

 	queue<vector<int>> q;
	q.push({ start_x, start_y });
	steps[start_x][start_y] = 0;
	int flag = 0, res = 0;
	while(!q.empty())
	{
		int x = q.front()[0], y = q.front()[1];
		q.pop();
		for(int i = 0; i < 4; ++i)
		{
			int newx = x + direction_x[i], newy = y + direction_y[i];
			if (newx < 0 || newx >= m || newy < 0 || newy >= m || grid[newx][newy] == 1 || steps[newx][newy] > -1)
				continue;
			else
			{
				if (grid[newx][newy] == 0)
					steps[newx][newy] = steps[x][y] + 1;
				if (grid[newx][newy] == 4)
					steps[newx][newy] = steps[x][y] + 3;
				if(grid[newx][newy] == 6)
				{
					steps[newx][newy] = steps[x][y] + 1;
					grid[newx][newy] = 0;
					queue<vector<int>> boom;
					boom.push({ newx, newy });
					while(!boom.empty())
					{
						for(int j = 0; j < 4; ++j)
						{
							int boomx = boom.front()[0] + direction_x[j], boomy = boom.front()[1] + direction_y[j];
							if(boomx >= 0 && boomx < m && boomy >= 0 && boomy < n)
							{
								if(grid[boomx][boomy] == 1)
								{
									grid[boomx][boomy] = 0;
								}
								if (grid[boomx][boomy] == 6)
								{
									grid[boomx][boomy] = 0;
									boom.push({ boomx, boomy });
								}
							}
						}
						boom.pop();
					}
				}
				if(grid[newx][newy] == 3)
				{
					flag = 1;
					res = steps[x][y] + 1;
				}
				q.push({ newx, newy });
			}
		}
		if(flag)
			break;
	}
	cout << res;*/
	return 0;
}

四、LeetCode_ACM模式输入_C++

4.1 cin >>

输入一个数字 或 字符 或 字符串
遇到“空格”、“TAB”、“回车”就结束

4.2 cin.getline()和getline(cin, )

cin.getline()属于istream流，而getline()属于string流，是不一样的两个函数。但是作用一样可以互换，都是可以输入带空格的字符串。其中getline和cin>>搭配时要注意。文章来源地址https://www.toymoban.com/news/detail-782774.html

4.3 示例输入为一维不定长数组输入

#include <bits/stdc++.h>
using namespace std;

int main() {
	vector<int> vec;
	int num;
	while(1) {
		cin >> num;
		vec.push_back(num);
		if (cin.get() == '\n') break;
	}
	
	return 0;
}

4.4 示例输入为"[1, 2, 3, 4, 5]"类似形式

// 也可以用双指针去写
#include <bits/stdc++.h>
using namespace std;

int main() {
	vector<int> nums;
	string tmp;
	string str;
	getline(cin, str);
	for (int i=1; i<str.size()-1; ++i) {
		if (str[i] == ',') {
			nums.push_back(stoi(tmp));
			tmp.clear();
			continue;
		}
		if (str[i] == ' ')
			continue;
		tmp += str[i];
	}
	nums.push_back(stoi(tmp));
	
	return 0;
}

到了这里，关于深度优先搜索（DFS）和广度优先搜索（BFS）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包