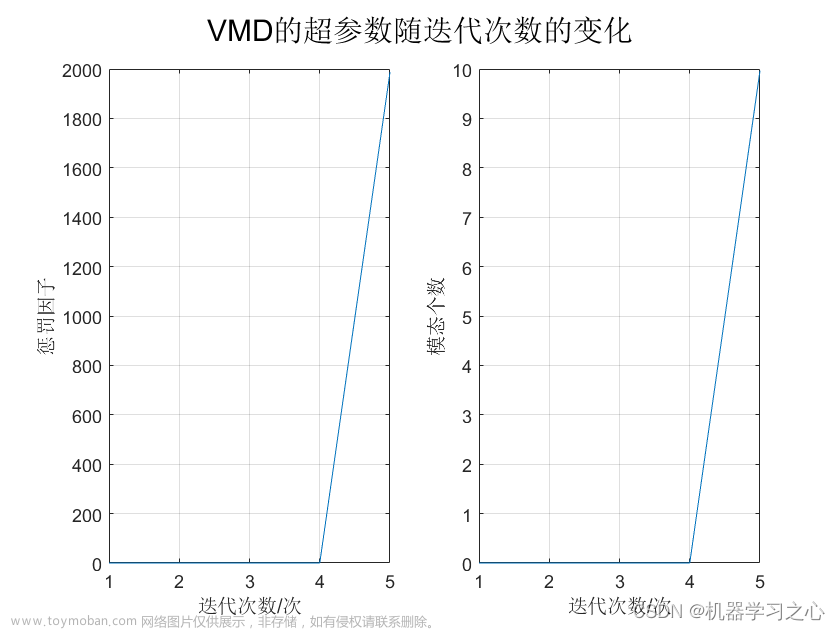
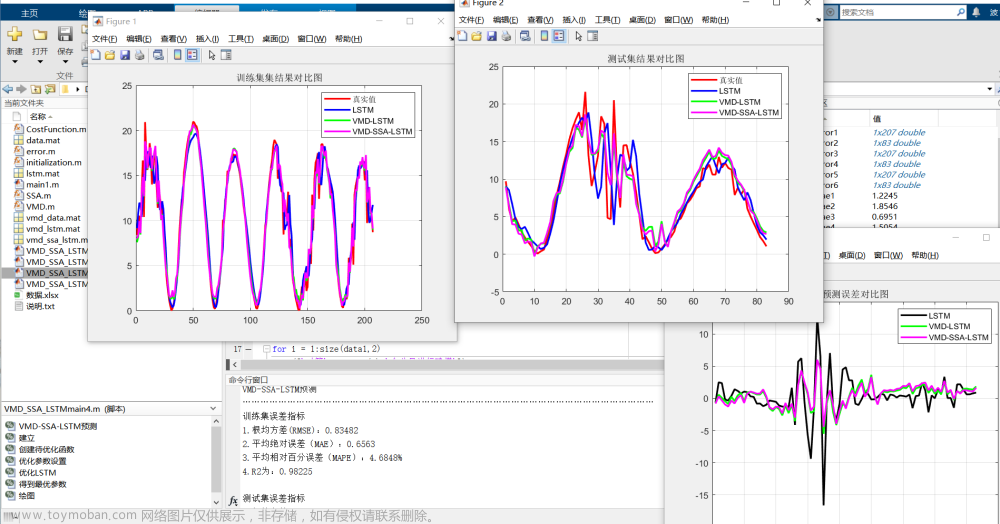
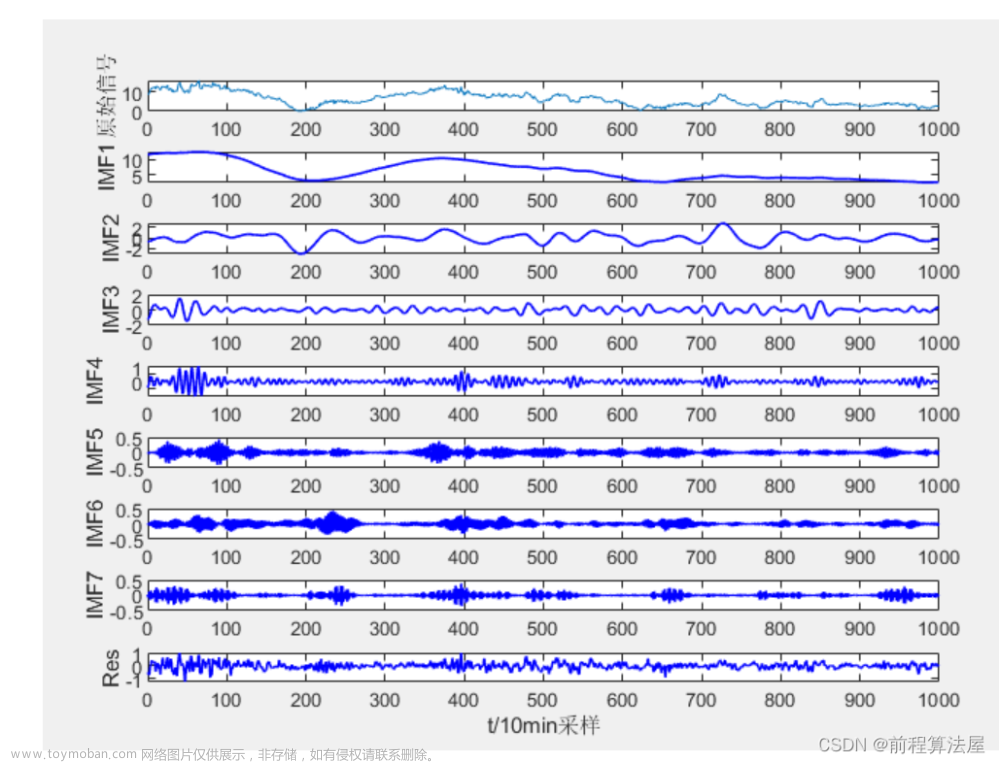
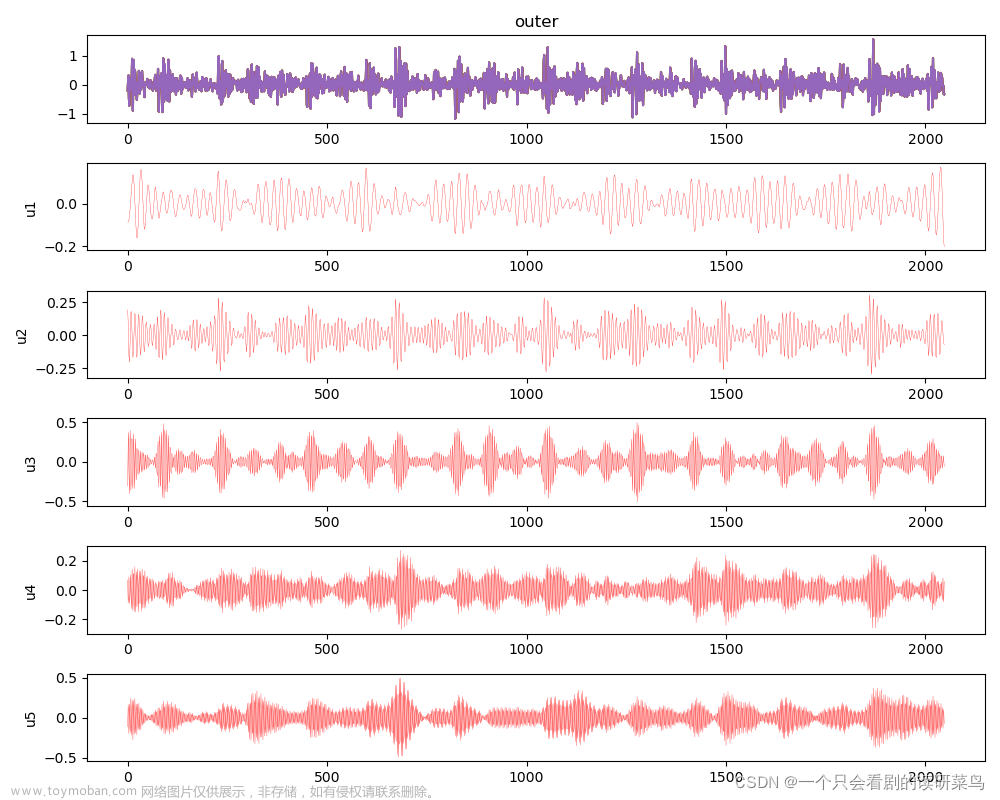
1 VMD算法原理
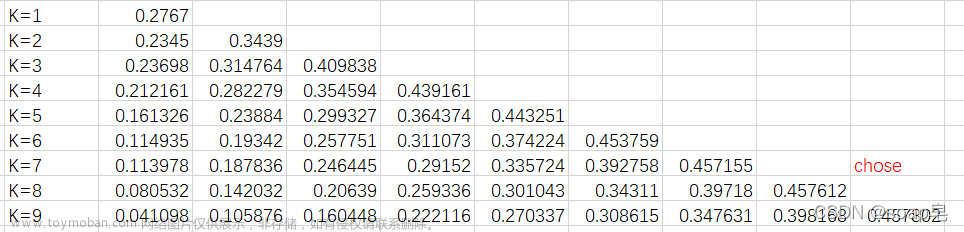
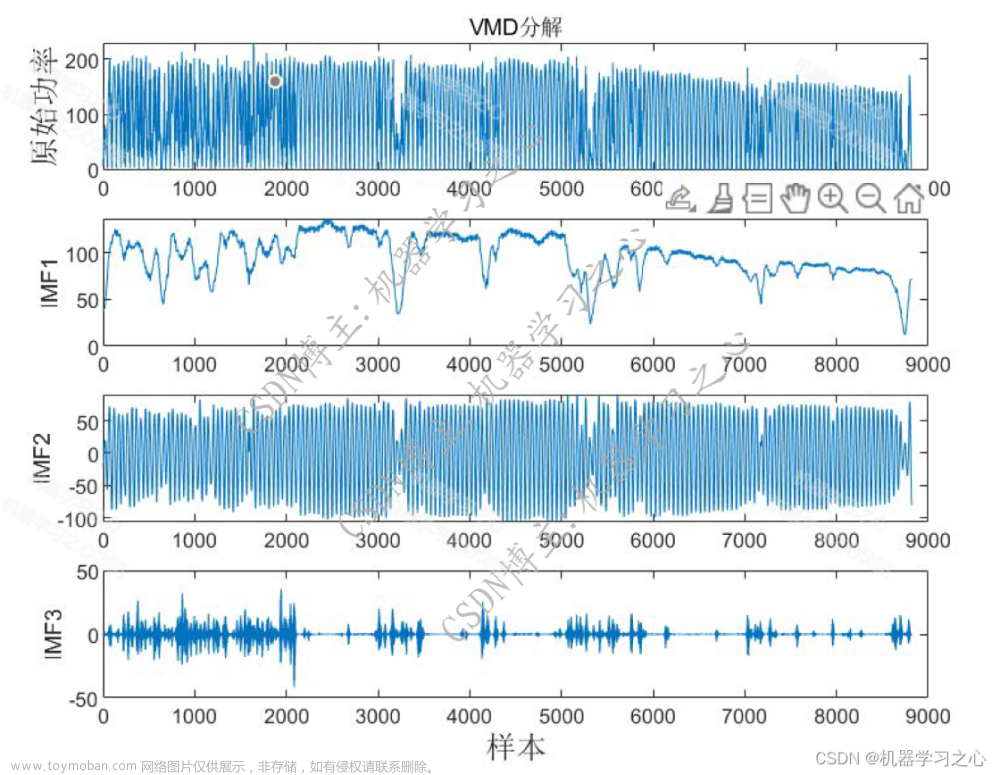
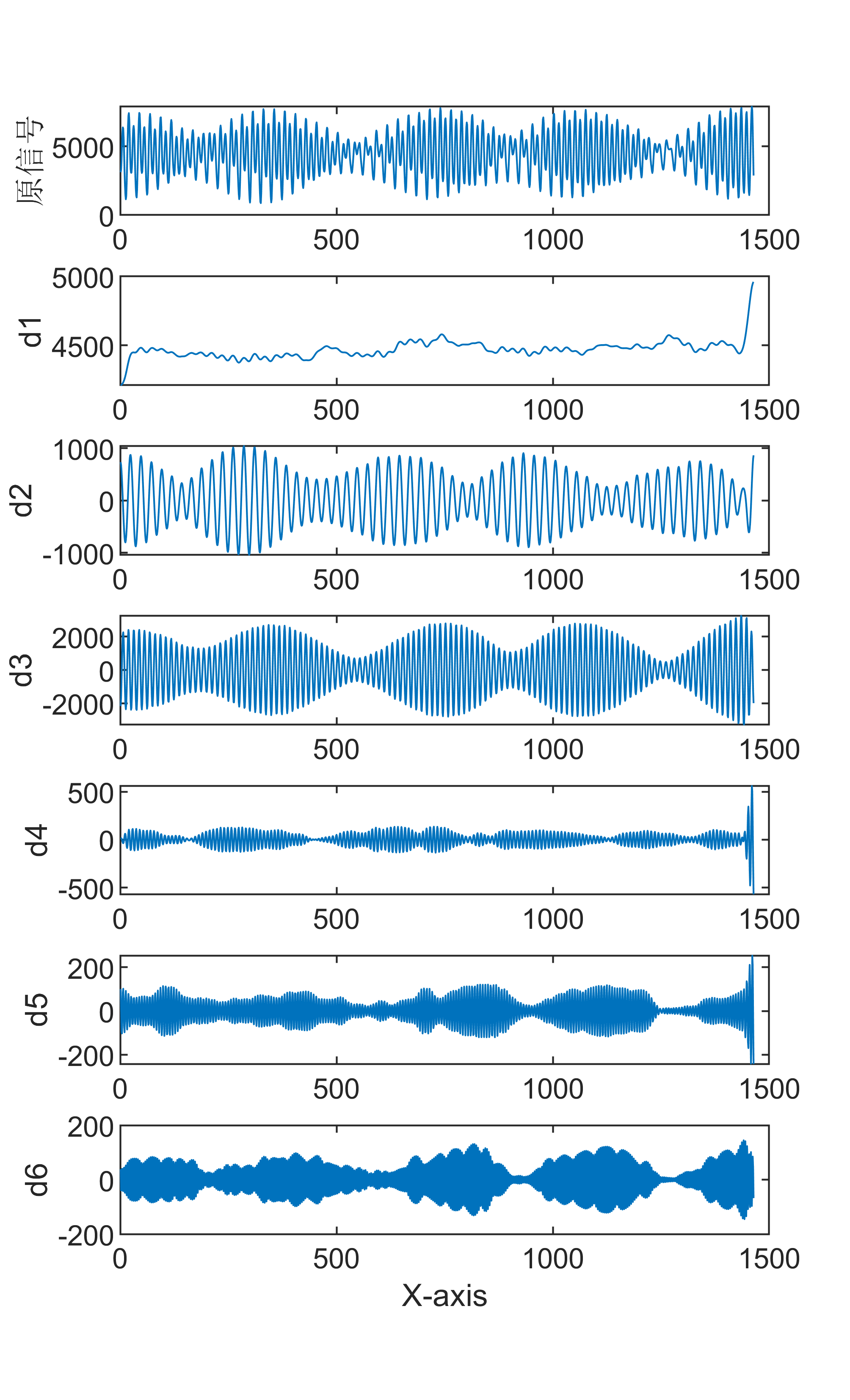
VMD的思想认为待分解信号是由不同IMF的子信号组成的。VMD为避免信号分解过程中出现模态混叠,在计算IMF时舍弃了传统信号分解算法所使用的递归求解的思想,VMD采用的是完全非递归的模态分解。与传统信号分解算法相比,VMD拥有非递归求解和自主选择模态个数的优点。该算法可将第j条线路的暂态零序电流信号分解为K个中心角频率为的本征模态函数,其中K为人为指定的模态分量个数。不同于EMD,VMD将每个IMF定义为调幅调频函数,可表示为:
 (1)
(1)
VMD算法可分为变分问题的构造和求解两部分:
(1)变分问题的构造:
 (2)
(2)
文章来源地址https://www.toymoban.com/news/detail-782991.html
①对暂态零序电流信号进行Hilbert变换,获得K个模态分量的解析信号,并得到单边频谱:
 (3)
(3)
式中为冲激函数。
②将各模态的频谱调制到基频带上,得到:
③计算式(3)梯度的平方范数,并估计每个模态信号的带宽,构造变分问题如下:
 (4)
(4)
(2)变分问题的求解
将上述约束性转化为非约束性变分问题,在式(4)中引入二次惩罚因子和拉格朗日乘法算子,扩展的拉格朗日表达式为:
 (5)
(5)
采用乘法算子交替方向法(Alternate Direction Method of Multipliers,ADMM)求解
function [u, u_hat, omega] = VMD(signal, alpha, tau, K, DC, init, tol)
% Variational Mode Decomposition
% Authors: Konstantin Dragomiretskiy and Dominique Zosso
% zosso@math.ucla.edu --- http://www.math.ucla.edu/~zosso
% Initial release 2013-12-12 (c) 2013
%
% Input and Parameters:
% ---------------------
% signal - the time domain signal (1D) to be decomposed
% alpha - the balancing parameter of the data-fidelity constraint2000或20000
% tau - time-step of the dual ascent ( pick 0 for noise-slack ) 0
% K - the number of modes to be recovered
% DC - true if the first mode is put and kept at DC (0-freq) 0
% init - 0 = all omegas start at 0
% 1 = all omegas start uniformly distributed
% 2 = all omegas initialized randomly
% tol - tolerance of convergence criterion; typically around 1e-6
%
% Output:
% -------
% u - the collection of decomposed modes
% u_hat - spectra of the modes
% omega - estimated mode center-frequencies
%
% When using this code, please do cite our paper:
% -----------------------------------------------
% K. Dragomiretskiy, D. Zosso, Variational Mode Decomposition, IEEE Trans.
% on Signal Processing (in press)
% please check here for update reference:
% http://dx.doi.org/10.1109/TSP.2013.2288675
%---------- Preparations
% Period and sampling frequency of input signal
save_T = length(signal);
fs = 1/save_T;
% extend the signal by mirroring
T = save_T;
f_mirror(1:T/2) = signal(T/2:-1:1);
f_mirror(T/2+1:3*T/2) = signal;
f_mirror(3*T/2+1:2*T) = signal(T:-1:T/2+1);
f = f_mirror;
% Time Domain 0 to T (of mirrored signal)
T = length(f);
t = (1:T)/T;
% Spectral Domain discretization
freqs = t-0.5-1/T;
% Maximum number of iterations (if not converged yet, then it won't anyway)
N = 500;
% For future generalizations: individual alpha for each mode
Alpha = alpha*ones(1,K);
% Construct and center f_hat
f_hat = fftshift((fft(f)));
f_hat_plus = f_hat;
f_hat_plus(1:T/2) = 0;
% matrix keeping track of every iterant // could be discarded for mem
u_hat_plus = zeros(N, length(freqs), K);
% Initialization of omega_k
omega_plus = zeros(N, K);
switch init
case 1
for i = 1:K
omega_plus(1,i) = (0.5/K)*(i-1);
end
case 2
omega_plus(1,:) = sort(exp(log(fs) + (log(0.5)-log(fs))*rand(1,K)));
otherwise
omega_plus(1,:) = 0;
end
% if DC mode imposed, set its omega to 0
if DC
omega_plus(1,1) = 0;
end
% start with empty dual variables
lambda_hat = zeros(N, length(freqs));
% other inits
uDiff = tol+eps; % update step
n = 1; % loop counter
sum_uk = 0; % accumulator
% ----------- Main loop for iterative updates
while ( uDiff > tol && n < N ) % not converged and below iterations limit
% update first mode accumulator
k = 1;
sum_uk = u_hat_plus(n,:,K) + sum_uk - u_hat_plus(n,:,1);
% update spectrum of first mode through Wiener filter of residuals
u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);
% update first omega if not held at 0
if ~DC
omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);
end
% update of any other mode
for k=2:K
% accumulator
sum_uk = u_hat_plus(n+1,:,k-1) + sum_uk - u_hat_plus(n,:,k);
% mode spectrum
u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);
% center frequencies
omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);
end
% Dual ascent
lambda_hat(n+1,:) = lambda_hat(n,:) + tau*(sum(u_hat_plus(n+1,:,:),3) - f_hat_plus);
% loop counter
n = n+1;
% converged yet?
uDiff = eps;
for i=1:K
uDiff = uDiff + 1/T*(u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i))*conj((u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i)))';
end
uDiff = abs(uDiff);
end
%------ Postprocessing and cleanup
% discard empty space if converged early
N = min(N,n);
omega = omega_plus(1:N,:);
% Signal reconstruction
u_hat = zeros(T, K);
u_hat((T/2+1):T,:) = squeeze(u_hat_plus(N,(T/2+1):T,:));
u_hat((T/2+1):-1:2,:) = squeeze(conj(u_hat_plus(N,(T/2+1):T,:)));
u_hat(1,:) = conj(u_hat(end,:));
u = zeros(K,length(t));
for k = 1:K
u(k,:)=real(ifft(ifftshift(u_hat(:,k))));
end
% remove mirror part
u = u(:,T/4+1:3*T/4);
% recompute spectrum
clear u_hat;
for k = 1:K
u_hat(:,k)=fftshift(fft(u(k,:)))';
end
end文章来源:https://www.toymoban.com/news/detail-782991.html
到了这里,关于变分模态分解(VMD)原理-附代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!