【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】-Toy模板网

这篇具有很好参考价值的文章主要介绍了【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

💃🏼 本人简介：男
👶🏼 年龄：18
📕 ps:七八天没更新了欸，这几天刚搞完元宇宙，上午一直练🚗，下午背四级单词和刷题来着，还在忙一些学弟学妹录制视频和准备开学一些事，一直没空出时间来，等 20号练完车，也马上开学了QAQ。不过今天倒是空出来一些时间，恰好这几天学到了dfs，原理和例题都很棒，谨以此篇作为学后的回顾总结！

1. dfs算法原理

1.1 dfs思想

深度优先搜索，简称dfs，简单讲就是一个搜索算法。

深搜是按照深度优先的方式进行搜索，通俗来讲就是一条路走到黑和不撞南墙不回头。
注意：这里的搜索并不是我们平时在文件上或网络上查找信息，而是通过一种穷举的方式，把所有可行的方案都列举出来，不断去尝试，直到找到问题的解。
具体来讲，dfs可以将“问题状态空间”看做一棵搜索树，深度优先就是从树根一直往下搜，遇到不可解就回溯，往其它方向继续向下扩展，像子集和和全排列问题，还有N皇后问题都可以深度优先搜索算法解决，它是一种暴力解决NP问题的非常直观的方法。
总的来说：DFS 用于找所有解的问题，它的空间效率高，而且找到的不一定是最优解，必须记录并完成整个搜索，故一般情况下，深搜需要非常高效的剪枝（剪枝的概念请百度）。

1.2 与递归区别

深搜是一种算法，注重的是思想；而递归是一种基于编程语言的实现方式。
深搜可以用递归实现，也就是说递归是我们用计算机编程语言实现深搜算法的手段。

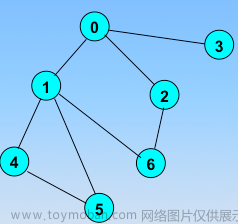
1.3 举例说明

如下图，灰色代表墙壁，绿色代表起点，红色代表终点，规定每次只能走一步，且只能往下或右走。求一条绿色到红色的最短路径。例子来源于这里

深度优先算法案例演示详解,# 算法,深度优先,算法,c++,dfs,深度优先遍历

用dfs来讲就是，先从绿点开始找准一个方向，并沿这个方向一直遍历，如果遇到障碍物不能继续遍历就回溯，返回上一个节点，直到找到终点为止。

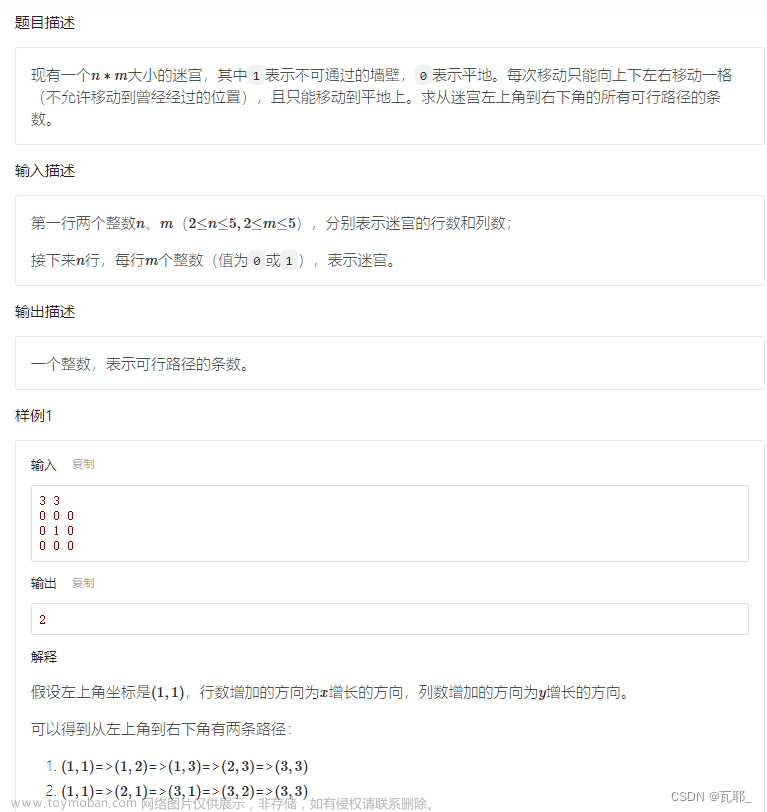
2. 经典例题——迷宫游戏

都学了这么多了。我们不妨来玩一个迷宫游戏巩固一下所学的算法！【迷宫如图下所示】

最短的解法如下图所示【大家答对了嘛】

2.1 题干信息

我们用一个二维字符数组来表示图画的迷宫。

S**.
....
***T

其中S表示起点，T表示终点，*表示墙壁，.表示平地。你需要从S出发走到T，每次只能向上下左右相邻的位置移动一位，不能走出地图，也不能穿过墙壁，每个点只能通过一次。用x表示你所要走的路线。

2.2 整体思路

我们从起点S开始，每走一步需要对上下左右一个方向一个方向地尝试，如果沿着某个方向不能走到终点，我们就要原路返回，继续尝试其他方向，直到走出迷宫。这是一种最朴素的走迷宫方式，虽然效率也许比较低，但如果迷宫有解，就一定能走出终点。
上面说的这种走法，就对应着今天学习的dfs算法。首先找到起点s,走到每个点时，按照左、下、右、上的顺序尝试。每走到下一个点以后，我们把这个点当做起点S，继续按顺序尝试。如果某个点上下左右四个方向都尝试过，便回到走到这个点之前的点，这一步我们称之为回溯。继续尝试其他方向。直到所有点都尝试过上下左右四个方向。
这就好比你自己去走这个迷宫，你也要一个方向一个方向的尝试着走，如果这条路不行就回头，尝试下一条路，dfs 的思想和我们直观的想法很类似。只不过，接下来我们需要用程序来完成这个过程。

2.3 细分拆解

第一步前的输入地图和变量设置，就不详细讲了，直接看代码即可

#include<iostream>
#include<stdio.h>
using namespace std;
int n, m;
char pos[150][150];	   //判断走没走过
bool trace[150][150];  //显示路径

int main() {
	//输入地图
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> pos[i][j];
		}
	}
	return 0;
}

①判断迷宫终点，记录所走路径

首先确定边界条件，当走到字符T时，我们找到了终点，从而结束搜索。所以边界条件判断为pos[x][y] == 'T'。
其次，为了防止走回头路，我们需要标记当前这个路径已走过，即当前这个点已走过，所以我们需要用trace[x][y]数组来做标记，为了显示出路径，走过的点我们用字符x表示。

bool dfs(int x, int y) {
	if (pos[x][y] == 'T') { //找到终点，返回true
		return true;
	}
	trace[x][y] = 1;		//若找不到，则trace数组标记为1表示已走过
	pos[x][y] = 'x';		//用pos显示最后的路径
}

②完善搜索与回溯，处理数组边界

结束操作处理好后，就要开始真正的搜索了。假设现在我们坐标为(x, y),分别遍历该坐标的上下左右位置，选择好依次进行方向的顺序后，一个方向一个方向进行访问，如果某一方向能走到终点，则返回true。
在上下左右遍历时，我们要考虑数组元素是否越界，此时我们就需要一个bool类型的check_in()函数进行判断。
注意：判断移动后位置能走的3个条件【缺一不可】
- ①没越界，在地图内；
- ②这个位置不是障碍物*，可以走到；
- ③该位置之前没走过

bool check_in(int x, int y) {	//	判断数组是否越界
	return (x > 0 && x <= n && y > 0 && y <= m); //这里表示的是如果()里为真，则返回true，否则返回false
}

bool dfs(int x, int y) {
	if (pos[x][y] == 'T') { //找到终点，返回true
		return true;
	}
	trace[x][y] = 1;		//若上下左右都找不到，则trace数组标记为1表示已走过
	pos[x][y] = 'x';		//用pos显示最后的路径

	int tx = x - 1, ty = y; //假设先往上走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) { //能移动到该位置的条件有三个：①没越界，在地图内； ②这个位置不是障碍物*，可以走到； ③该位置之前没走过
		if (dfs(tx, ty)) {	//对移动后位置进行判断是不是终点，如果是，返回true，如果不是，在对其上下左右判断。
			return true;
		}
	}

	tx = x, ty = y - 1; //如果往上走行不通，则选择向左走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
		if (dfs(tx, ty)) {
			return true;
		}
	}

	tx = x + 1, ty = y; //如果往左走行不通，则选择向下走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
		if (dfs(tx, ty)) {
			return true;
		}
	}

	tx = x , ty = y + 1; //如果往下走行不通，则选择向右走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
		if (dfs(tx, ty)) {
			return true;
		}
	}

	pos[x][y] = '.';	//	如果一个位置的上下左右都走不了，则取消该位置的路径进行回溯，回溯过程把之前已标记的'x'改回'.'
	trace[x][y] = 0;//只找可行路线的话，trace可改可不改。但如果找全部解，则需要恢复
	return false;
}

大家有没有发现判断上下左右是否可行时，主题代码是不是都是一样的欸？所以大家可以想一下，能怎么去优化一下嘛，在这里我卖个关子，咱们后面马上讲！

③找寻迷宫起点，打印结束路径

我们费心费力地把迷宫主体的dfs的函数写完了，但我们该从哪开始呢？结束条件如何设置呢？

int main() {
	//输入地图
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> pos[i][j];
		}
	}
	cout << "----------------------------------------" << endl;

	//找寻起点
	int x , y ; //定义x，y用于保存迷宫起点时的位置
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (pos[i][j] == 'S') {
				x = i, y = j;
			}
		}
	}
	if (dfs(x, y)) { //如果能找到终点，则打印迷宫显示其路径
		cout << "鼠鼠我欸，已到达终点啦，路线如下: " << endl;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				cout << pos[i][j];
			} cout << endl;
		}
	}
	else {
		cout << "鼠鼠我欸，走不出去啦awa" << endl;
	}
	return 0;
}

2.4 总体代码展示

#include<iostream>
#include<stdio.h>
using namespace std;

int n, m;
char pos[150][150];	   //判断走没走过
bool trace[150][150];  //显示路径

bool check_in(int x, int y) {	//	判断数组是否越界
	return (x > 0 && x <= n && y > 0 && y <= m); //这里表示的是如果()里为真，则返回true，否则返回false
}

bool dfs(int x, int y) {
	if (pos[x][y] == 'T') { //找到终点，返回true
		return true;
	}
	trace[x][y] = 1;		//若上下左右都找不到，则trace数组标记为1表示已走过
	pos[x][y] = 'x';		//用pos显示最后的路径

	int tx = x - 1, ty = y; //假设先往上走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) { //能移动到该位置的条件有三个：①没越界，在地图内； ②这个位置不是障碍物*，可以走到； ③该位置之前没走过
		if (dfs(tx, ty)) {	//对移动后位置进行判断是不是终点，如果是，返回true，如果不是，在对其上下左右判断。
			return true;
		}
	}

	tx = x, ty = y - 1; //如果往上走行不通，则选择向左走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
		if (dfs(tx, ty)) {
			return true;
		}
	}

	tx = x + 1, ty = y; //如果往左走行不通，则选择向下走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
		if (dfs(tx, ty)) {
			return true;
		}
	}

	tx = x , ty = y + 1; //如果往下走行不通，则选择向右走
	if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
		if (dfs(tx, ty)) {
			return true;
		}
	}

	pos[x][y] = '.';	//	如果一个位置的上下左右都走不了，则取消该位置的路径进行回溯，回溯过程把之前已标记的'x'改回'.'
	trace[x][y] = 0;//只找可行路线的话，trace可改可不改。但如果找全部解，则需要恢复
	return false;
}
int main() {
	//输入地图
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> pos[i][j];
		}
	}
	cout << "----------------------------------------" << endl;
	//找寻起点
	int x , y ; //定义x，y用于保存迷宫起点时的位置
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (pos[i][j] == 'S') {
				x = i, y = j;
			}
		}
	}
	if (dfs(x, y)) { //如果能找到终点，则打印迷宫显示其路径
		cout << "鼠鼠我欸，已到达终点啦，路线如下: " << endl;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				cout << pos[i][j];
			} cout << endl;
		}
	}
	else {
		cout << "鼠鼠我欸，走不出去啦awa" << endl;
	}
	return 0;
}

2.5 测试样例

深度优先算法案例演示详解,# 算法,深度优先,算法,c++,dfs,深度优先遍历

2.6 代码优化

前面提到，我们在对下一位置进行上下左右判断时，需要写四个主体相同的代码。为了减少代码量，我们不妨写一个循环，用一个二维数组依次表示四个方向，进而进行判断。

int dir[4][2] = { { -1 , 0 } , { 0 , -1 } , { 1 ,  0 } , { 0 , 1 } };
//	按逆时针依次表示     向上	      向左		 向下	         向右	
//第一个数表示x(行)变化，第二个表示y(列)变化
bool dfs(int x, int y) {
	if (dfs(x, y) == 'T') {
		return true;
	}
	trace[x][y] = 1;
	pos[x][y] = 'x';
	for (int i = 1; i <= 4; i++) {  //1、2、3、4依次表示上、左、下、右
		int tx = x + dir[i][0]; //表示x加上第几个方向的第1个数，即行变化，
		int ty = y + dir[i][1];  //表示x加上第几个方向的第2个数，即列变化，
		if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
			if (dfs(tx, ty)) {
				return true;
			}
		}
	}
	pos[x][y] = '.';	//	如果一个位置的上下左右都走不了，则取消该位置的路径进行回溯，回溯过程把之前已标记的'x'改回'.'
	trace[x][y] = 0;//只找可行路线的话，trace可改可不改。但如果找全部解，则需要恢复
}

优化后代码

#include<iostream>
#include<stdio.h>
using namespace std;

int n, m;
char pos[150][150];	   //判断走没走过
bool trace[150][150];  //显示路径
		int dir[4][2] = { { -1 , 0 } , { 0 , -1 } , { 1 ,  0 } , { 0 , 1 } };
//	按逆时针依次表示     向上	      向左		 向下	         向右	
//第一个数表示x(行)变化，第二个表示y(列)变化

bool check_in(int x, int y) {	//	判断数组是否越界
	return x > 0 && x <= n && y > 0 && y <= m; //这里表示的是如果()里为真，则返回true，否则返回false
}

bool dfs(int x, int y) {
	if (dfs(x, y) == 'T') {
		return true;
	}
	trace[x][y] = 1;
	pos[x][y] = 'x';
	for (int i = 1; i <= 4; i++) {  //1、2、3、4依次表示上、左、下、右
		int tx = x + dir[i][0]; //表示x加上第几个方向的第1个数，即行变化，
		int ty = y + dir[i][1];  //表示x加上第几个方向的第2个数，即列变化，
		if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {
			if (dfs(tx, ty)) {
				return true;
			}
		}
	}
	pos[x][y] = '.';	//	如果一个位置的上下左右都走不了，则取消该位置的路径进行回溯，回溯过程把之前已标记的'x'改回'.'
	trace[x][y] = 0;//只找可行路线的话，trace可改可不改。但如果找全部解，则需要恢复

}


int main() {
	//输入地图
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> pos[i][j];
		}
	}
	cout << "----------------------------------------" << endl;
	//找寻起点
	int x , y ; //定义x，y用于保存迷宫起点时的位置
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (pos[i][j] == 'S') {
				x = i, y = j;
			}
		}
	}
	if (dfs(x, y)) { //如果能找到终点，则打印迷宫显示其路径
		cout << "鼠鼠我欸，已到达终点啦，路线如下: " << endl;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				cout << pos[i][j];
			} cout << endl;
		}
	}
	else {
		cout << "鼠鼠我欸，走不出去啦awa" << endl;
	}
	return 0;
}

最后，感谢大家支持u （^ _ ^）

如果感觉这篇文章对你有帮助的话，不妨三连支持下，十分感谢(✪ω✪)。文章来源地址https://www.toymoban.com/news/detail-783260.html

printf("点个赞吧*^*");

cout << "收藏一下叭o_o";

System.out.println("评论一下吧^_^");

print("关注一下叭0-0")

到了这里，关于【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】