数据结构 | 链式二叉树【递归的终极奥义】-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构 | 链式二叉树【递归的终极奥义】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🌳链式二叉树的结构及其声明

在上一节中，我们说到了一种数据结构——【堆】。也看到了一些有关二叉树的基本雏形，在本节中，我们就来说说有关这种链式二叉树的具体实现以及应用

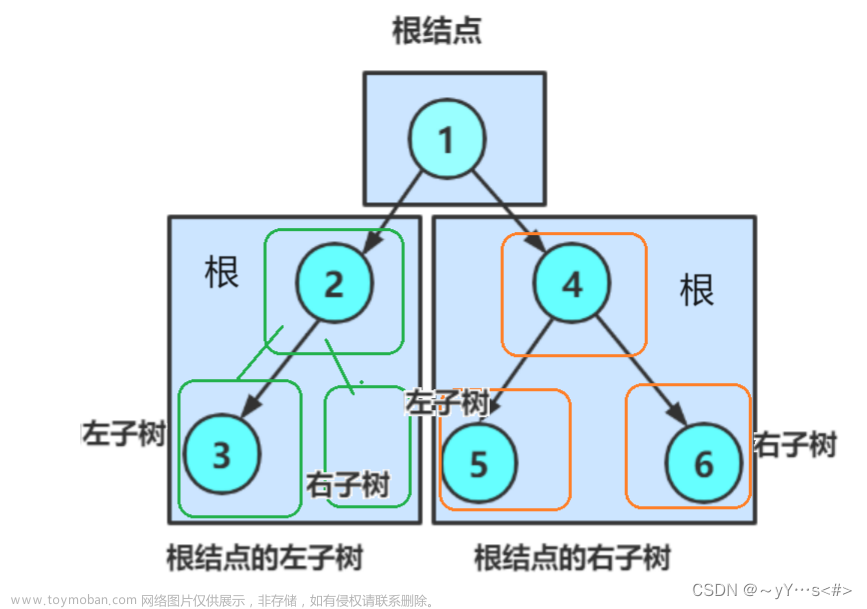
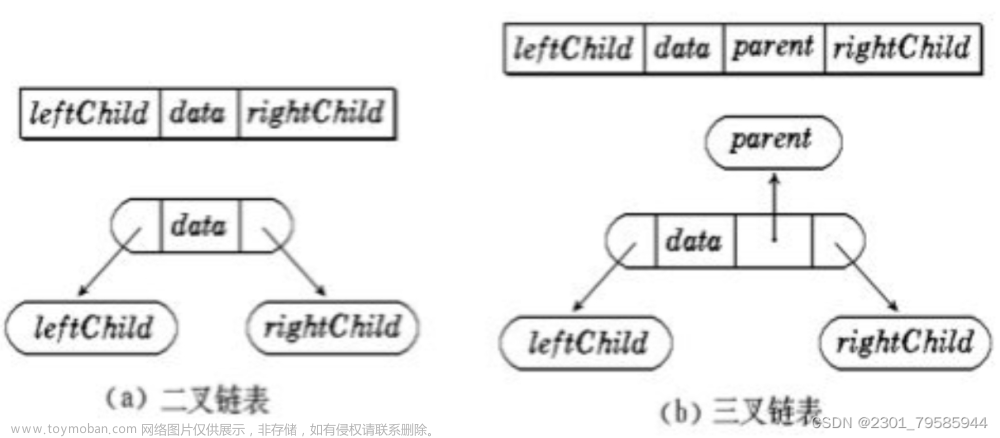
首先来看看它的结构声明。结构体中有三个成员，一个是当前结点的值，还有两个是指向当前结点左孩子结点的指针以及指向右孩子结点的指针

typedef int BTDataType;
typedef struct BinaryTreeNode {
	BTDataType data;
	struct BinaryTreeNode* lchild;
	struct BinaryTreeNode* rchild;
}BTNode;

也就是下面这种样子

🌳链式二叉树的四种遍历方式

好，知道了链式二叉树的基本结构之后，我们就要去了解如何去遍历出这棵树。对于链式二叉树的遍历方式有四种，我们逐个来讲讲

🌊先序遍历（先根遍历）

规则：根——左子树——右子树

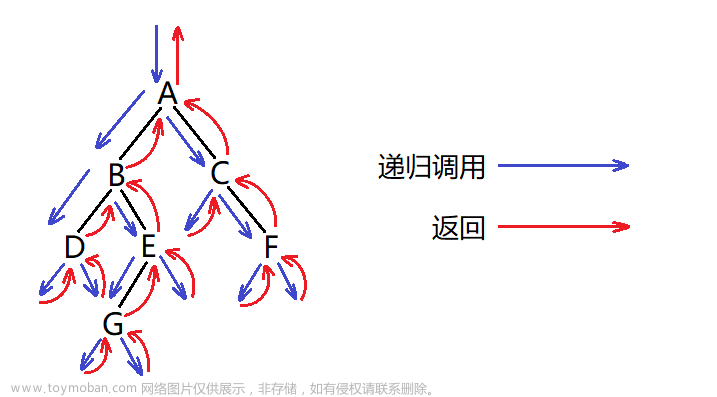
首先看一下有关先序遍历的的算法算法解析图【我画了很久的/(ㄒoㄒ)/~~】

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

有关先序遍历，了解了上面的规则之后可以知道，每次去遍历都是【根——左子树——右子树】，为什么说每次呢，从上图可知有关二叉树的遍历我们要使用递归来实现，也即是当访问完根之后去访问左子树，这个时候左子树不可以直接访问，而是要继续依照【根——左子树——右子树】这种规则去进行一个访问，即将【2】当做这一棵子树的根，遍历完2之后继续去遍历它的左子树，依次类推。。。
因此我们可以将这棵树通过层层递归划分成若干个区域，如下图所示
温馨提示：颜色有点多，可能看不太清楚，主要是为了理解递归的区间划分

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

了解了这些之后，我们就可以轻而易举地写出有关先序遍历的序列了，可能你在学校里面写的就只是【1 2 3 4 5 6】这样，没错，这就是先序序列，但是在本文中，我要带你彻底搞定出递归的真正含义，所以我会将访问的空结点也表示出来，也就是NULL

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

这么对照着看，应该清晰一些了，有关二叉树的遍历这一块重要的还是自己理解，多画画图，后期如果时间我录个视频再放上来讲解一下

递归算法图解

接着我们通过画递归展开图来进一步了解一下是如何进行先序遍历的

代码展示

/*先序遍历*/
void PreOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->lchild);
	PreOrder(root->rchild);
}

🌊中序遍历（中根遍历）

规则：左子树——根——右子树

了解了前序遍历，那中序遍历也不下话下。和先序做一个区分

代码展示

/*中序遍历*/
void InOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	PreOrder(root->lchild);
	printf("%d ", root->data);
	PreOrder(root->rchild);
}

🌊后序遍历（后根遍历）

规则：左子树——右子树——根

后序遍历也是一样的套路

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

代码展示

/*后序遍历*/
void PostOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	PreOrder(root->lchild);
	PreOrder(root->rchild);
	printf("%d ", root->data);
}

🌊层次遍历

当然，除了前序、中序、后序以外还有一种遍历方法就是层次遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

辅助队列思维

对于层序遍历呢，它和前中后序不一样，只是简单的递归，我们要使用到另一个数据结构来进行配合解决，那就是【队列】，有关这种思路的讲解，可以看看我的N叉树的层序遍历，或者是在本文的末尾中有关二叉树的面试题汇总中也要层序遍历相关的例题，这里就不作过多分析

代码详解

👉来讲一下思路

对于层序遍历，我们需要有一个队列，对其初始化后首先将根结点入队，之后的操作就是放在一个循环中进行，结束条件是【队列为空】
保存下队头结点遍历打印。接着将其出队并且入队其左右孩子结点，以此循环往复直到队列为空，就遍历完了二叉树中的所有节点

/*层序遍历*/
void LevelOrder(BTNode* root)
{
	Qu q;
	QueueInit(&q);
	
	if (root != NULL)		//首先将非空根结点入队
		QueuePush(&q,root);

	while (!QueueEmpty(&q))
	{
		QDataType front = QueueFront(&q);	//首先获取队头结点
		printf("%d ", front->data);			//获取到之后输出打印
		QueuePop(&q);		//将其出队

		//将其左右孩子结点再从队尾入队
		if (front->lchild)
			QueuePush(&q, front->lchild);
		if(front->rchild)
			QueuePush(&q, front->rchild);
	}

	QueueDestroy(&q);
}

🌳链式二叉树进阶算法实现

刚才在初步了解了链式二叉树后学习了四种其遍历方式，但是遍历一棵链式二叉树并不是很难在二叉树这一节估计只有1到2分的难度，真正难的还在后面呢😵

🍃求树的结点个数——难度系数【⭐⭐】

Way1：变量累加法

首先看到要求一棵树的结点个数，那我猜你想到的一定是去定义一个变量，然后去进行一个递归调用，每调用一次count++，但是这样的话很明显不可以，这一点我们首先得否决，在C语言函数的局部变量那一块我们有讲过，对于局部变量出了作用域就会销毁，因此你对于每一次的递归调用单独建立的栈帧都会存在这个局部变量，但是呢在栈帧销毁之后这个变量也就跟着销毁了，所以这种办法不可以取

int TreeNodeNum1(BTNode* root)
{
	if (root == NULL)
		return;
	int sz = 0;
	sz++;
	TreeNodeNum1(root->lchild);
	TreeNodeNum1(root->rchild);
	return sz;
}

于是有同学呢又想出一种办法，就是将这个变量定义为静态变量，因为静态变量是存放在静态区中的，不会随着某一个函数的调用结束而销毁，因此我们可以这么写

int TreeNodeNum1(BTNode* root)
{
	if (root == NULL)
		return;
	static int sz = 0;
	sz++;
	TreeNodeNum1(root->lchild);
	TreeNodeNum1(root->rchild);
	return sz;
}

可以看到，第一次的计算确实是可以计算出来这棵树有6个结点，但是在我多调用几次之后结点个数却发生了一个累加，这就是静态变量的特点，均会在上一次的基础上去进行一个运算，无论你是调用其他的什么函数或者是多调用几次，那其实可以看到这里就出现BUG了，
我们该如何去进行修改呢？
其实这一块很简单，我们不需要静态变量，直接将这个变量放到函数外部，作为一个全局变量即可，因为函数内部的返回值我们不好控制，干脆就不要返回值，直接将这个记数的变量定义为全局变量，这样就很好控制了

int sz = 0;
void TreeNodeNum1(BTNode* root)
{
	if (root == NULL)
		return;
	sz++;
	TreeNodeNum1(root->lchild);
	TreeNodeNum1(root->rchild);
}

我们再来测试一下。可以看到每次的结点个数算出来均是恒定不变的，就是每次在上一次调用完求值之后要将sz重新置为0

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

Way2：分治递归法

很显然对于上述的这种变量累加法，并不能体现出链式二叉树的特性，接下去我们使用一种分治递归法去求解，这种方法的思路很简单也很好理解
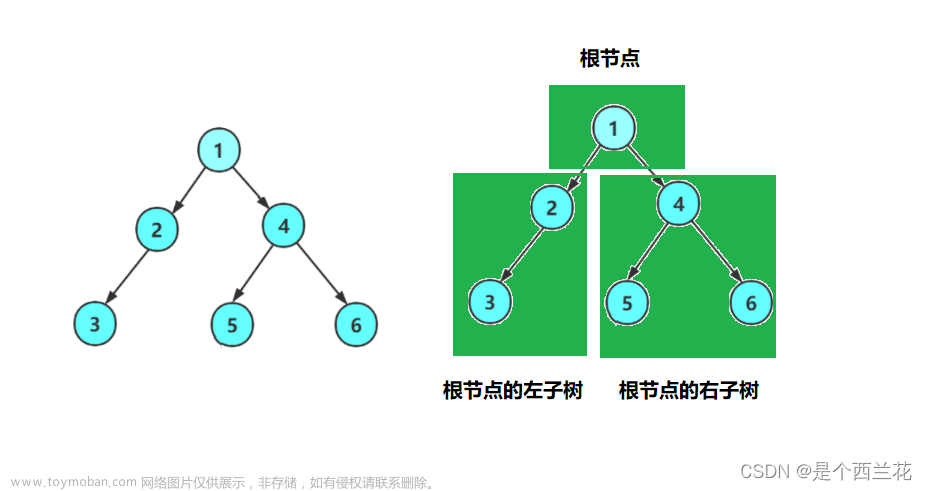
我们始终将一个树分割为三个部分，【根】【左子树】【右子树】，因此进行一个分块求解然后再加起来就可以了

情景思路分析

这个听起来是很好理解，但是递归这种结构的话对于有些同学来说还是比较晦涩难懂的，因此我们通过一个特殊的情景来分析一下

疫情结束，马上就要返校复工了，此时学校需要统计有多多少人会返校，于是这件事情就交给副校长去办
假设每个领导最多只能管理两个人，现在呢副校长他想要了解到两个院系有多个人，那么他就要去询问两个副院长，也就是链式二叉树所对应的左右子树；那对于副院长呢，它想要知道这个院里有多少个人，那就需要找到每个班级对应的班主任去询问；然而对于班主任呢，班级方面的事情他就交给班长去负责，统计出班里有多少人返校
当班长搜集完信息后就汇报给班主任，班主任再汇报给副院长，最后副院长再汇报给副校长。副校长接收到一个副院长的统计汇报后再向另一个副院长去询问，返校人数信息，这对应的就是先访问完左子树之后再访问右子树，最后当另一个副院长也将人数汇报上来之后再加上他自己就是本次返校的人数了【当然这只是假设】

具体的图解如下
数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

以下是代码

int TreeNodeNum(BTNode* root)
{
	return root == NULL ? 0 :
		TreeNodeNum(root->lchild) + TreeNodeNum(root->rchild) + 1;
}

看到代码，这里是使用了一个三目运算符，当然你也可以写成if语句判断的形式，只是这样写比较简洁一些，可以看到，就是一个对左子树和右子树的分别递归，最后再加上1，也就是根节点

以下是递归算法图解

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

如果你感觉自己对于链式二叉树的递归这一块不是很清楚的话，就像我这样画画递归的图解吧，可以有助于对代码的理解，因为对于递归这种结构只看代码的话是很难理解的，通过画图分析就可以清楚很多
后面的题目也是一样，我会带着你画，你也可试着自己去画画看，就是递归的调用和回调的一个过程，注重递归出口就行

🍃求树的叶子结点个数——难度系数【⭐⭐🌙】

警惕空指针❗

会求一棵树中的所有结点数，现在我们来进阶一下，求解树的叶子结点个数，如果不知道什么是叶子结点的话，建议看看树和二叉树的基本概念
知道了如何去求解总的结点个数，那求叶子结点并不难，当然也是使用递归去完成，只是每次在递归的时候就是左子树和右子树的累加和，不要加上自己就行
于是有同学就写了这样的代码，我们来看看有什么问题

int TreeLeafSize(BTNode* root)
{
	if (root->lchild == NULL && root->rchild == NULL)
		return 1;		//若是左右孩子均为空，则表示只有结点
	return TreeLeafSize(root->lchild) + TreeLeafSize(root->rchild);
}

首先从根结点开始，左右孩子均不为空则往下递归，若是当前结点的孩子结点为空，则表示其为叶子结点，return 1返回上一级，递归完左子树之后再递归右子树，从下图可以看出，当递归2的左子树之后去递归2的右子树时，就会出现【访问空指针】的异常⚠

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

DeBug调试观测

这一块我们一起带VS来调试一下看看

首先看到现在递归进到了2的左子树，data值为3，其左右孩子均为NULL，因为可以断定其为叶子结点，因为便返回上一级

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

然后可以看到回到结点2了

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

继续往右子树进行递归

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

那我们该用什么办法去解决呢？这个很简单，只需要判断一下当前递归进来的结点是否为空，也就是【root == NULL】，若是空的话就返回即可
所以将代码改为如下

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->lchild == NULL && root->rchild == NULL)
		return 1;		//若是左右孩子均为空，则表示只有结点
	return TreeLeafSize(root->lchild) + TreeLeafSize(root->rchild);
}

测试一下可以看到这棵树的叶子结点有3个

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🍃求树的高度——难度系数【⭐⭐⭐】

规则明细及思路分析

接下去，我们再将难度提升一个档次，会求结点个数了，现在去求求这棵树的高度是多少。首先我给出计算规则，防止大家跑偏

📚规则：二叉树高度 = 左子树和右子树中高度大的那个 + 1

知道了规则，我们就可以通过画图来理一下思路。可以看到我给3加了一个右孩子结点。接着从肉眼就可以看出对于根节点1来说其左子树的高度为3，右子树的高度为2，所以整棵树的高度就为3 + 1 = 4

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

错误案例示范——怎么就是不长记性(╯▔皿▔)╯

接下去我们来看一个错误的案例释放，这也是很多同学会犯的错误，而且会导致很严重的重复计算❌
可以看到这位同学就是将我们的算法图转化为了代码，递归式地去比较左右子树的高度，最后找出大的那个 + 1

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeHeight(root->lchild) > TreeHeight(root->rchild) ?		
		   TreeHeight(root->lchild) + 1 : TreeHeight(root->rchild) + 1;
}

从运行结果可以看出是可以计算出来的，树的高度为4，但是呢却存在一个很大的隐患

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

为什么这么说呢，因为这样的写法在LeetCode上提交是会【超时】的，超时是什么？就是算法设计得过于复杂，程序运行的时间过长，但是那位同学说：就光几行代码而已，就算是递归也就只有4高度的树而已，最多也就是十几次的递归和回调，怎么可能会超时呢❓
然后我是这么解释的

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

这里看下来你应该可以明白了，原因就在于递归进去结点的时候比较完左右子树的高度没有将其保存起来，这样就会导致在求解每一棵子树的时候都需要向下重新递归直到空为止，也就造成了【重复计算】
每往上求解一个结点的高度下面的结点就需要多递归一次，随着逐层向上求解，下面每一个结点的递归次数就是一个并不是2倍的上升，而是一个指数级别甚至阶乘级别的上升，这取决于这棵树的深度，若是深度越深，那递归层数就会越多，就会导致什么？就会导致栈内存不够然后栈溢出
因此大家应该要认识到，这种写法是一种极大地浪费资源，那我们应该怎么办呢，很简单，将每次左右子树递归进去回调后的结果做一个保存即可

正确代码描述【递归算法图解】

所以正确的代码应该想下面这样，将当前结点递归进去的后左右子树求出的高度做一个保存，然后对他们再进行一个比较。这样就不会出现上述的问题了，而且代码看起来还比较简洁

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int LHeight = TreeHeight(root->lchild);
	int	RHeight = TreeHeight(root->rchild);

	return LHeight > RHeight ? LHeight + 1 : RHeight + 1;		//返回左右子树中大的那一个再加上根结点
}

下面是算法图解

图解很大，截不了图，可以看看我的架构然后自己试着画画图

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🍃求第K层有多少个结点——难度系数【⭐⭐⭐🌙】

思路分析及规则明细

好，会求结点数，会求高度，对于树的层次也有了一个概念后，我们就要再进一步去考虑更加复杂些的问题，那就是去求解第K层有多少个结点，这个我们应该怎么去求解呢？一起来画画图分析一下吧
假设要求解的是【第三层有多少结点个数】
从上图你应该可以看出我是什么意思了，这也需要一种递归的思维，对于根节点①来说，是第三层；但是对于②和④来说确实第二层，而对于③、⑤、⑥来说是第一层，只需要按照相对位置往下走就可以了。因此我们可以得出这样运算规则：

规则：
📚当k > 1 时，第k层的结点个数为其左孩子的第k - 1层 + 其右孩子的第k - 1层结点个数
📚当k == 1时，return 1

代码描述

所以很明确，根据思路，就可以写出如下代码
除了判断k之外，别忘了每次都要判断一下传进来的根结点是否为空，防止访问空指针。然后对于左右孩子的递归就是【k - 1】，每往其左右孩子递归一次，k就-1，递归出口就是当【k == 1】时，return 1即可

int TreeNodeNumK(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeNodeNumK(root->lchild, k - 1)
		+ TreeNodeNumK(root->rchild, k - 1);
}

这么看代码一定也会很抽象吧，那就试着自己对着代码去画画算法图吧，以下是我的分析过程

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🍃查找指定结点——难度系数【⭐⭐⭐】

学会了【统计】，我们来学学【查找】

错误案例示范——有些人走着走着就散了🚶‍

首先我们来看看一位同学的错误代码

/*查找指定结点*/
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (!root)			
		return NULL;
	if (root->data == x)
		return root;		//若根节点就是所要查找的结点，则直接返回
		
	TreeFind(root->lchild, x);
	TreeFind(root->rchild, x);
	//没有理解清楚递归的返回过程
}

在学习了上面的统计结点个数、叶子结点个数以及第K层的结点个数，虽然代码并不复杂，而且我带大家画了递归展开图，所以有些同学就认为对于二叉树的题目都可以这么去写
乍一看上面的代码其实没有什么问题，首先判断递归传入的根是否为空，然后再判断其是否就为我们要查找的结点，若都不满足就继续递归其左右子树，但是呢仔细看可以看出来，每次递归下去再回调回来的值有谁去接收呢？所以最后只会是返回一个随机值

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

可以看到，在查找完之后去打印，出来的就是一个空值，因为根本就没有拿一个变量去接收一下，所以在半路就丢了

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

正确代码展示及分析

这里其实和前面求解二叉树的高度是一样的，在递归进去左右子树再返回回来时，要拿一个变量去接收一下才行，这样才能保证查找到那个正确的值，而不是在半路就丢了，走散了

如果对于if(!root)不理解的，那一定是!操作符没掌握，看看我的操作符汇总大全

BTNode* TreeFind(BTNode* root, BTDataType x)
{
	/*
	* if (root == NULL)和if(!root)是等价的
	* if(root) - 结点是存在的
	* if(!root) - 结点是不存在的 --> 空的
	* if (root == NULL) -->空的
	* if (root != NULL) -->非空
	*/
	//if (root == NULL)
	//	return NULL;
	if (!root)			
		return NULL;
	if (root->data == x)
		return root;		//若根节点就是所要查找的结点，则直接返回
	/*
	* 要保存下当前查找的结点，否则递归回来没有接收返回的只会是一个空值或者随机值
	*/
	BTNode* ret1 = TreeFind(root->lchild, x);
	if (ret1)
		return ret1;		//表明在左子树中找到了该结点，返回
	BTNode* ret2 = TreeFind(root->rchild, x);
	if (ret2)
		return ret2;		//表明在右子树中找到了该结点，返回
	
	return NULL;			//左右子树均没有找到，返回NULL
}

可以看到，这里在递归左右子树的时候，我分别都拿了一个指向结点的指针接收了一下，然后在递归回调的时候就可以接收到找到的这个返回值了，接着再去判断一下其是否存在，若是存在就将其return即可
我们来跟着画一下它的递归算法展开图

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

可以看到，有返回值去接收了，就不至于在半路丢失，可以一层一层地返回回来，最后把结果给到外界的调用
我们再来看看运行结果

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🍃判断二叉树是否为完全二叉树——难度系数【⭐⭐⭐⭐】

接下来，继续做一个进阶，在树和二叉树的基本概念中，我讲到了两种特殊的二叉树：满二叉树和完全二叉树，所以在这里我们要判断一棵树是否为完全二叉树，该如何去做呢？

概念分析及规则明细

我们知道，对于完全二叉树来说，最下面一层的叶子都依次排列在改成最左边的位置上，也就是中间不可以或缺，或者说是空出一个，这样的话就不能算是完全二叉树。下面是例图📃

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

所以我们就可以得出运算规则

📚若遇到的空结点后还有非空的结点，则表明其不为完全二叉树
📚若遇到的空结点后均为空，则表示其为完全二叉树

有了这个运算规则之后呢我们就可以去将其转化为代码了，这个逻辑是要嵌套在二叉树的层序遍历中的，层序遍历这一块的题目我也是有做过相关的题解，而且在下面模块的OJ算法题实训中也有讲到，可以去看看，直接套用模板即可

代码描述及分析

首先给出代码

/*判断二叉树是否为完全二叉树*/
bool TreeComplete(BTNode* root)
{
	Qu qu;
	QueueInit(&qu);

	if (root)
		QueuePush(&qu, root);		//首选入队队头结点

	while (!QueueEmpty(&qu))
	{
		QDataType front = QueueFront(&qu);
		QueuePop(&qu);

		//判断当前队列结点是否为空
		if (front == NULL)
			break;		//若为空，则break跳出循环进行判断
		else
		{
			//若不为空，则入队其左右孩子
			QueuePush(&qu, front->lchild);
			QueuePush(&qu, front->rchild);
		}
	}

	//此处判断是否为完全二叉树
	/*
	* 1.若遇到的空结点后还有非空的结点，则表示其不为完全二叉树
	* 2.若遇到的空结点后均为空，则表明其为完全二叉树
	*/
	if (!QueueEmpty(&qu))
	{			
		QDataType front = QueueFront(&qu);
		if (front != NULL)
		{				//若是在队列中取到了非空的结点，则表示不为完全二叉树
			QueueDestroy(&qu);		//提前return要记得销毁队列
			return false;
		}

	}
	return true;
	QueueDestroy(&qu);
}

看到上述代码，应该可以知道为什么这个算法可以被赋四颗星了吧，相比其他进阶算法来说确实需要一些二叉树的基本能力
但是呢，有了我给你的这个思路之后再去写代码其实也不是什么难事，我们只需要在一些地方做一个修改就可以了。首先第一个地方就是在刚获取到当前队头结点的时候，此时不要着急去入左右孩子结点，需要做一些改动，而且对于层序遍历所涉及的OJ题基本也是在这个地方去做一个改动
什么时候跳出循环呢？但是在内层进行判断肯定不行，最好做一个分离，外层判断，那也就需要使用到【break】，跳出当前的循环，那要什么时候跳出呢？刚才看了那张图应该可以知道有一个转折点应该是在层序遍历到NULL的时候，此时我们应该跳出循环
那要怎么判断呢？回忆完全二叉树的定义可以知道，但凡你遇到NULL了之后就相等于是断层了，后面若是再出现有结点那就说明不是完全二叉树，我们可以根据这点去判断队列是否为空，然后知晓后面是否还有结点需要遍历。这个就是跳出循环后的判断逻辑了

注意：在判断出不为完全二叉树后提前【return false】了，就需要将队列销毁，否则会造成内存泄漏

再来看看运行结果

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🍃销毁二叉树

思路分析

对一棵二叉树进行了一系列的操作之后，我们要去肯定要去销毁这棵二叉树，否则也会造成内存泄漏
但是这要怎么去完成呢？从根节点开始往下销毁吗？设想你先将根节点销毁了，那左右子树不是找不到了，就和你删除链表结点是一个道理，改变了这个指向原本的指向也就是找不到了
因此我们不应该从根结点开始，应该先从左右子树开始，那对于左子树来说它又可以作为一个根结点，依旧是需要先去销毁其左右子树，右子树也是一样，因此这就又成了一个【递归】的问题。而且是要销毁掉左右子树之后再去销毁根结点，所以这就相当于是一种后序遍历的思维

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

代码描述

来展示一下代码

/*销毁二叉树*/
void DestroyTree(BTNode* root)
{
	if (root == NULL)		//if(!root)
		return;

	DestroyTree(root->lchild);
	DestroyTree(root->rchild);

	free(root);	//只有释放完当前结点的左右子树后，才能销毁当前根节点
}

代码很简洁，当还没遍历到空树时，就一直递归遍历其左子树，然后进行销毁，接着return回去销毁右子树，最后再销毁根结点
但是这里有一点要注意的是对于内部的销毁是无法因此外部变化的，这个相信你在看了本文后也有所领会，因此我们要在外界函数调用完后再对指向根节点的指针置空，防治野指针

DestroyTree(n1);
n1 = NULL;		//内部置空外部也要置空【形参改变不影响实参】

🌳整体代码展示

bree.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <cstring>

typedef int BTDataType;
typedef struct BinaryTreeNode {
	BTDataType data;
	struct BinaryTreeNode* lchild;
	struct BinaryTreeNode* rchild;
}BTNode;

/*开辟结点*/
BTNode* BuyBTNode(BTDataType x);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(char* a, int* pi);
/*先序遍历*/
void PreOrder(BTNode* root);
/*中序遍历*/
void InOrder(BTNode* root);
/*后序遍历*/
void PostOrder(BTNode* root);
/*层序遍历*/
void LevelOrder(BTNode* root);
/*求树的结点个数——2分*/
//void TreeNodeNum1(BTNode* root);
int TreeNodeNum1(BTNode* root);
int TreeNodeNum2(BTNode* root);
/*求树的叶子结点个数——2.5分*/
int TreeLeafSize(BTNode* root);
/*求树的高度——3分*/
int TreeHeight(BTNode* root);
/*求第K层有多少个结点——3.5分*/
int TreeNodeNumK(BTNode* root, int k);
/*查找指定结点*/
BTNode* TreeFind(BTNode* root, BTDataType x);
/*判断二叉树是否为完全二叉树*/
bool TreeComplete(BTNode* root);
/*销毁二叉树*/
void DestroyTree(BTNode* root);

bree.cpp

#define _CRT_SECURE_NO_WARNINGS 1

#include "btree.h"
#include "queue.h"


BTNode* BuyBTNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	node->data = x;
	node->lchild = node->rchild = NULL;

	return node;
}

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(char* a, int* pi)
{
	//若为空树
	if (a[(*pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}
	
	//普通情况，开辟结点存储
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->data = a[(*pi)++];
	
	//递归当前结点的左右子树
	node->lchild = BinaryTreeCreate(a, pi);
	node->rchild = BinaryTreeCreate(a, pi);

	return node;
}

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%d ", root->data);
	PreOrder(root->lchild);
	PreOrder(root->rchild);
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->lchild);
	//printf("%d ", root->data);
	printf("%c ", root->data);
	InOrder(root->rchild);
}

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->lchild);
	PostOrder(root->rchild);
	printf("%d ", root->data);
}

/*层序遍历*/
void LevelOrder(BTNode* root)
{
	Qu q;
	QueueInit(&q);
	
	if (root != NULL)		//首先将非空根结点入队
		QueuePush(&q,root);

	while (!QueueEmpty(&q))
	{
		QDataType front = QueueFront(&q);	//首先获取队头结点
		printf("%d ", front->data);			//获取到之后输出打印
		QueuePop(&q);		//将其出队

		//将其左右孩子结点再从队尾入队
		if (front->lchild)
			QueuePush(&q, front->lchild);
		if(front->rchild)
			QueuePush(&q, front->rchild);
	}

	QueueDestroy(&q);
}

/*求树的结点个数——2分*/
//int sz = 0;
//void TreeNodeNum1(BTNode* root)
//{
//	if (root == NULL)
//		return;
//	sz++;
//	TreeNodeNum1(root->lchild);
//	TreeNodeNum1(root->rchild);
//}

int TreeNodeNum1(BTNode* root)
{
	if (root == NULL)
		return 0;
	static int sz = 0;
	sz++;
	TreeNodeNum1(root->lchild);
	TreeNodeNum1(root->rchild);
	return sz;
}

int TreeNodeNum2(BTNode* root)
{
	return root == NULL ? 0 :
		TreeNodeNum2(root->lchild)
		+ TreeNodeNum2(root->rchild) + 1;
}

/*求树的叶子结点个数——2.5分*/
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->lchild == NULL && root->rchild == NULL)
		return 1;		//若是左右孩子均为空，则表示只有结点
	return TreeLeafSize(root->lchild) + TreeLeafSize(root->rchild);
}

/*求树的高度——3分*/

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeHeight(root->lchild) > TreeHeight(root->rchild) ?
		TreeHeight(root->lchild) + 1 : TreeHeight(root->rchild) + 1;
}
//int TreeHeight(BTNode* root)
//{
//	if (root == NULL)
//		return 0;
//	int LHeight = TreeHeight(root->lchild);
//	int	RHeight = TreeHeight(root->rchild);
//
//	return LHeight > RHeight ? LHeight + 1 : RHeight + 1;		//返回左右子树中大的那一个再加上根结点
//
//	//return TreeHeight(root->lchild) > TreeHeight(root->rchild) ?		
//	//						TreeHeight(root->lchild) + 1 : TreeHeight(root->rchild) + 1
//	// —— 非常浪费空间，需要重复调用多次	--> 班主任没记性
//}

/*求第K层有多少个结点——3.5分*/
int TreeNodeNumK(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeNodeNumK(root->lchild, k - 1)
		+ TreeNodeNumK(root->rchild, k - 1);
}

/*查找指定结点*/


//BTNode* TreeFind(BTNode* root, BTDataType x)
//{
//	if (!root)
//		return NULL;
//	if (root->data == x)
//		return root;		
//
//	TreeFind(root->lchild, x);
//	TreeFind(root->rchild, x);
//}


BTNode* TreeFind(BTNode* root, BTDataType x)
{
	/*
	* if (root == NULL)和if(!root)是等价的
	* if(root) - 结点是存在的
	* if(!root) - 结点是不存在的 --> 空的
	* if (root == NULL) -->空的
	* if (root != NULL) -->非空
	*/
	//if (root == NULL)
	//	return NULL;
	if (!root)
		return NULL;
	if (root->data == x)
		return root;		//若根节点就是所要查找的结点，则直接返回
	/*
	* 要保存下当前查找的结点，否则递归回来没有接收返回的只会是一个空值或者随机值
	*/
	BTNode* ret1 = TreeFind(root->lchild, x);
	if (ret1)
		return ret1;		//表明在左子树中找到了该结点，返回
	BTNode* ret2 = TreeFind(root->rchild, x);
	if (ret2)
		return ret2;		//表明在右子树中找到了该结点，返回

	return NULL;			//左右子树均没有找到，返回NULL
}
/*判断二叉树是否为完全二叉树*/
bool TreeComplete(BTNode* root)
{
	Qu qu;
	QueueInit(&qu);

	if (root)
		QueuePush(&qu, root);		//首选入队队头结点

	while (!QueueEmpty(&qu))
	{
		QDataType front = QueueFront(&qu);
		QueuePop(&qu);

		//判断当前队列结点是否为空
		if (front == NULL)
			break;		//若为空，则break跳出循环进行判断
		else
		{
			//若不为空，则入队其左右孩子
			QueuePush(&qu, front->lchild);
			QueuePush(&qu, front->rchild);
		}
	}

	//此处判断是否为完全二叉树
	/*
	* 1.若遇到的空结点后还有非空的结点，则表明若遇到的空结点后均为空，则表示其为完全二叉树其不为完全二叉树
	* 2.
	*/
	if (!QueueEmpty(&qu))
	{			
		QDataType front = QueueFront(&qu);
		if (front != NULL)
		{				//若是在队列中取到了非空的结点，则表示不为完全二叉树
			QueueDestroy(&qu);		//提前return要记得销毁队列
			return false;
		}

	}
	return true;
	QueueDestroy(&qu);
}

/*销毁二叉树*/
void DestroyTree(BTNode* root)
{
	if (root == NULL)		//if(!root)
		return;

	DestroyTree(root->lchild);
	DestroyTree(root->rchild);

	free(root);
}

test.cpp

#define _CRT_SECURE_NO_WARNINGS 1

#include "btree.h"

void test()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);

	n1->lchild = n2;
	n1->rchild = n4;

	n2->lchild = n3;
	n4->lchild = n5;
	n4->lchild = n5;
	n4->rchild = n6;

	PreOrder(n1);		//n1即为根结点
	printf("\n");

	InOrder(n1);		//n1即为根结点
	printf("\n");

	PostOrder(n1);		//n1即为根结点
	printf("\n");

	LevelOrder(n1);		//n1即为根结点
	printf("\n");
}

void test2()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);

	n1->lchild = n2;
	n1->rchild = n4;

	n2->lchild = n3;
	n4->lchild = n5;
	n4->rchild = n6;

	PreOrder(n1);		//n1即为根结点
	printf("\n");

	//int sz = 0;
	//sz = TreeNodeNum1(n1);
	//printf("树的结点个数为：%d\n", sz);
	//sz = TreeNodeNum1(n1);
	//printf("树的结点个数为：%d\n", sz);
	//sz = TreeNodeNum1(n1);
	//printf("树的结点个数为：%d\n", sz);

	//int sz = 0;
	//TreeNodeNum1(n1);
	//printf("树的结点个数为：%d\n", sz);

	//sz = 0;
	//TreeNodeNum1(n1);
	//printf("树的结点个数为：%d\n", sz);

	//sz = 0;
	//TreeNodeNum1(n1);
	//printf("树的结点个数为：%d\n", sz);
	
	//int num1 = TreeNodeNum2(n1);
	//printf("树的结点个数为：%d\n", num1);

	//int num2 = TreeLeafSize(n1);
	//printf("树的叶子结点个数为：%d\n", num2);

	//int num3 = TreeNodeNumK(n1, 3);
	//printf("树的第3层结点个数为：%d\n", num3);
}

void test3()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	BTNode* n7 = BuyBTNode(7);
	BTNode* n8 = BuyBTNode(8);

	n1->lchild = n2;
	n1->rchild = n4;

	n2->lchild = n3;
	n4->lchild = n5;
	n4->rchild = n6;

	n3->lchild = n7;
	n3->lchild = n8;

	int height = TreeHeight(n1);
	printf("树的高度为：%d\n", height);
}

void test4()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	BTNode* n7 = BuyBTNode(7);
	n1->lchild = n2;
	n1->rchild = n4;

	n2->lchild = n3;
	n2->rchild = n7;
	n4->lchild = n5;
	n4->rchild = n6;

	//BTNode* FindX = TreeFind(n1, 5);
	//if (FindX)
	//	printf("找到该结点了，其值为：%d\n", FindX->data);
	//else
	//	printf("没有找到：%p\n",FindX->data);
	//printf("查找的值为：%p\n", TreeFind(n1, 5));

	bool ret = TreeComplete(n1);
	if (ret)
		printf("是完全二叉树\n");
	else
		printf("不是完全二叉树\n");

	DestroyTree(n1);
	n1 = NULL;		//内部置空外部也要置空【形参改变不影响实参】
}

void test5()
{
	char str[] = "ABD##E#H##CF##G##";
	int i = 0;
	BTNode* root = BinaryTreeCreate(str, &i);

	InOrder(root);		//中序遍历一下这棵树
}

//前序遍历
void My_PreOrder(BTNode* root, int* a, int* pi)
{
	if (root == NULL)
		return;
	a[(*pi)++] = root->data;
	My_PreOrder(root->lchild, a, pi);
	My_PreOrder(root->rchild, a, pi);
}


int* preorderTraversal(BTNode* root, int* returnSize) {
	//1.获取二叉树的结点个数
	*returnSize = TreeNodeNum2(root);

	//2.根据结点个数开辟数组
	int* a = (int*)malloc(sizeof(int) * (*returnSize));
	memset(a, 0, sizeof(int) * (*returnSize));
	//3.前序遍历
	int i = 0;
	My_PreOrder(root, a, &i);

	return a;
}

void test6()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);

	n1->rchild = n2;
	n2->lchild = n3;

	int sz = 0;
	int *a = preorderTraversal(n1, &sz);
	for (int i = 0; i < sz; ++i)
	{
		printf("%d ", a[i]);
	}
}

bool isSameTree(BTNode* root1, BTNode* root2)
{
	if (!root1 && !root2)
		return true;
	if (!root1 || !root2)
		return false;
	if (root1->data != root2->data)
		return false;
	return isSameTree(root1->lchild, root2->lchild)
		&& isSameTree(root1->rchild, root2->rchild);
}

bool isSubtree(BTNode* root, BTNode* subRoot) {
	//子树不可能为空，若主树为空则找不到子树
	if (!root)
		return false;
	if (isSameTree(root, subRoot))
		return true;

	return isSubtree(root->lchild, subRoot)            //左树找到了就不需要再去右树寻找了
		|| isSubtree(root->rchild, subRoot);
}
void test7()
{
	BTNode* root1 = BuyBTNode(3);
	BTNode* n2 = BuyBTNode(4);
	BTNode* n3 = BuyBTNode(5);
	BTNode* n4 = BuyBTNode(1);
	BTNode* n5 = BuyBTNode(2);

	root1->lchild = n2;
	root1->rchild = n3;
	n2->lchild = n4;
	n2->rchild = n5;

	BTNode* root2 = BuyBTNode(4);
	BTNode* n6 = BuyBTNode(1);
	BTNode* n7 = BuyBTNode(2);

	root2->lchild = n6;
	root2->rchild = n7;


	bool ret = isSubtree(root1, root2);
	if (ret)
		printf("可以找到子树\n");
	else
		printf("找不到子树\n");
}
int main(void)
{
	//test();
	//test2();
	test3();
	//test4();
	//test5();
	//test6();
	//test7();
	return 0;
}

🌳算法接口测试

后来补充的，测试一下进阶写的各种算法接口，加深理解💪

首先来看一下四种遍历

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

求解二叉树的结点个数

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

求解二叉树的叶子结点个数

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

求解二叉树的高度

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

求解二叉树的第K层叶子结点个数

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

查找二叉树中的指定结点

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

判断二叉树是否为完全二叉树

数据结构 | 链式二叉树【递归的终极奥义】,# 数据结构,数据结构,递归,二叉树

🌳链式二叉树OJ算法题实训

本模块请于我另一个专栏【LeetCode算法笔记】进行观看

也可直接点击此链接

🌳总结与提炼

学习完了链式二叉树，我们来总结一下所学习的知识点📖

首先我们了解了这种链式二叉树的数据结构，知道了它由左右孩子以及结点值组成
接下去了解有关链式二叉树的四种遍历方式，分别是先序、中序、后序以及层次遍历，这里主要是使用递归的形式去求解，非递归的思路我们后续在【数据结构进阶】中再做讲解
然后呢我们在了解了基本的遍历算法后对二叉树有了一些进阶算法的训练，分别是【求解树的结点个数】、【叶子结点个数】、【高度】、【第K层结点个数】、【查找指定结点】、【判断是否为完全二叉树以及销毁】等，有了这些进阶训练后，对于二叉树这种数据结构也有了进一步地了解
接下去就是实战训练，我们通过十余道OJ算法题的训练，做了一些有关二叉树的实际应用，对二叉树更上一个台阶
二叉树这种数据结构无论是在笔试、面试或者考研中都是非常重要的，作为读者的你是否有感受到呢？