数据结构:链式二叉树初阶

目录

一.链式二叉树的逻辑结构

1.链式二叉树的结点结构体定义

2.链式二叉树逻辑结构

二.链式二叉树的遍历算法

1.前序遍历

2.中序遍历

3.后序遍历 

4.层序遍历(二叉树非递归遍历算法)

层序遍历概念:

层序遍历算法实现思路: 

层序遍历代码实现:

三.链式二叉树遍历算法的运用

1.前序遍历算法的运用

相关练习: 

2.后序遍历算法的运用

3.层序遍历算法的运用

问题来源:

四.链式二叉树其他操作接口的实现

1. 计算二叉树结点个数的接口

2.计算二叉树叶子结点的个数的接口

3.计算二叉树第k层结点个数的接口

4.二叉树的结点查找接口(在二叉树中查找值为x的结点)

一.链式二叉树的逻辑结构

1.链式二叉树的结点结构体定义

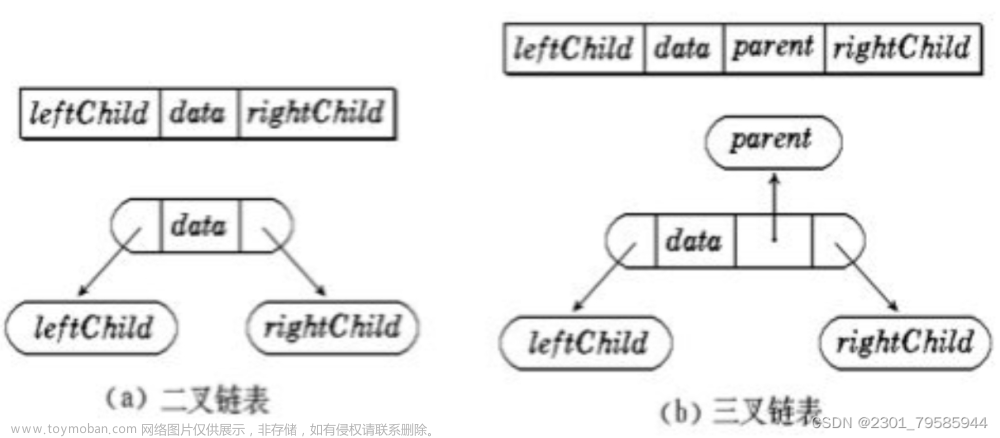
• 树结点结构体定义:

  ​
  typedef int BTDataType;
  typedef struct BinaryTreeNode
  {
  	BTDataType data;                //数据域
  	struct BinaryTreeNode* left;    //指向结点左孩子的指针
  	struct BinaryTreeNode* right;   //指向结点右孩子的指针
  }BTNode;
  
  ​

2.链式二叉树逻辑结构

• 这里先暴力"创建"一颗二叉树:

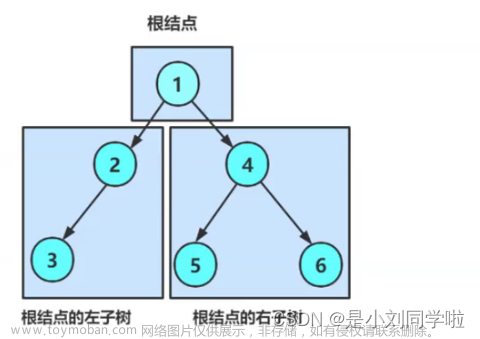
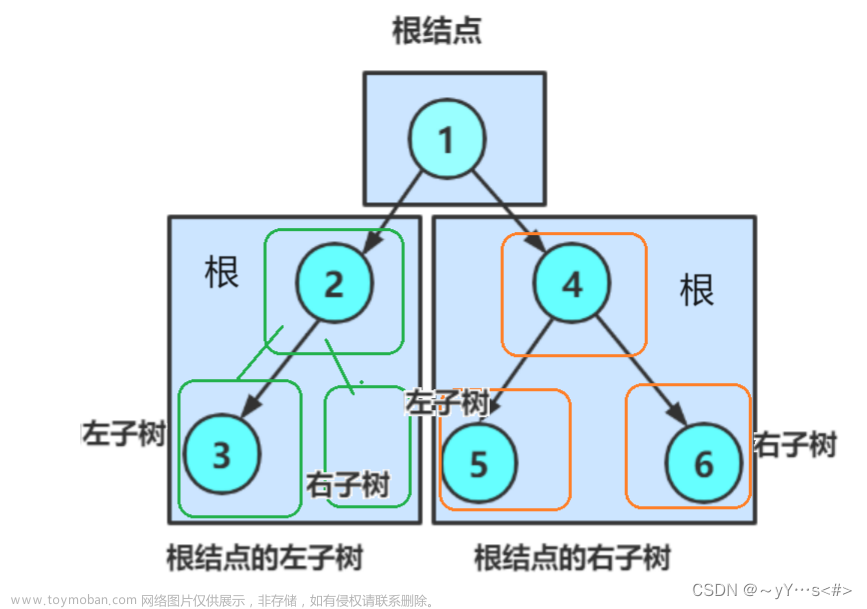
  //在内存堆区上申请结点的接口
  BTNode* BuyNode( BTDataType x)
  {
  	BTNode* tem = (BTNode*)malloc(sizeof(BTNode));
  	assert(tem);
  	tem->data = x;
  	tem->left = NULL;
  	tem->right = NULL;
  	return tem;
  }

  int main ()
  {
      BTNode* node1 = BuyNode(1);
  	BTNode* node2 = BuyNode(2);
  	BTNode* node3 = BuyNode(3);
  	BTNode* node4 = BuyNode(4);
  	BTNode* node5 = BuyNode(5);
  	BTNode* node6 = BuyNode(6);
  	node1->left = node2;
  	node1->right = node4;
  	node2->left = node3;
  	node4->left = node5;
  	node4->right = node6;
  
      //其他操作
      return 0;
  }

• 树的逻辑结构图示:

1. 每个树结点都有其左子树和右子树

2. 因此关于链式二叉树的递归算法的设计思路是:关于树T的问题可以分解为其左子树和右子树的问题,树T的左子树和右子树的问题又可以以同样的方式进行分解,因此就形成了递归

3. 关于链式二叉树递归算法的核心思维:左右子树分治思维。

二.链式二叉树的遍历算法

遍历二叉树的递归框架:

1. 函数的抽象意义是完成整棵树的遍历
2. 为了完成整棵树的遍历我们先要完成该树的左子树的遍历和右子树的遍历
3. 左子树和右子树的遍历又可以以相同的方式进行问题拆分,于是便形成了递归(数学上的递推迭代)

//递归遍历二叉树的基本函数结构
void Order(BTNode* root)
{
	if (NULL == root)
	{
		return;
	}

	对当前结点进行某种处理的语句位置1(前序);
	Order(root->left);  //遍历左子树的递归语句
	对当前结点进行某种处理的语句位置2(中序);
	Order(root->right); //遍历右子树的递归语句
	对当前结点进行某种处理的语句位置3(后序);
}

• 通过这个递归函数,我们可以遍历二叉树的每一个结点:(假设根结点的地址为root)
• 根据函数中对当前的root结点进行某种处理的代码语句的位置可将遍历二叉树的方式分为前序遍历(位置1),中序遍历(位置2),后序遍历(位置3)三种

1.前序遍历

//二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (NULL == root)
	{
		printf("NULL->");//为了方便观察我们将空结点打印出来
		return;
	}
	printf("%d->", root->data); //当前结点处理语句
	PreOrder(root->left);       //向左子树递归
	PreOrder(root->right);      //向右子树递归
}

• 以图中的树为例调用前序遍历函数:

  PreOrder(root); //root为树根地址

  递归函数执行过程中函数栈帧的逻辑结构分布以及代码语句执行次序图示:

  递归函数执行过程中函数栈帧的物理结构分布:

1. 当递归执行到图中的第4步是函数栈帧的物理结构:

2. 当递归执行到图中的第10步是函数栈帧的物理结构: 

3. 当递归执行到图中的第14步是函数栈帧的物理结构: 

4. 当递归执行到图中的第22步是函数栈帧的物理结构: 

• 递归函数执行过程中同一时刻开辟的函数栈帧的最大个数取决于树的高度:因此递归遍历二叉树的空间复杂度为:O(logN);

2.中序遍历

//二叉树中序遍历
void InOrder(BTNode* root)
{
	if (NULL == root)
	{
		printf("NULL->");   //为了方便观察我们打印出空结点
		return;
	}
	InOrder(root->left);        //向左子树递归
	printf("%d->", root->data); //打印结点值(root处理语句)
	InOrder(root->right);       //向右子树递归
}

•  递归函数执行过程分析方法与前序遍历类似
• 对于图中的二叉树,中序遍历的结点值打印次序为:

3.后序遍历 

//二叉树后序遍历
void BackOrder(BTNode* root)
{
	if (NULL == root)
	{
		printf("NULL->");       //为了方便观察我们打印出空结点
		return;
	}
	BackOrder(root->left);      //向左子树递归
	BackOrder(root->right);     //向右子树递归
	printf("%d->", root->data); //打印结点值(root处理语句)
}

•  递归函数执行过程分析方法与前序遍历类似
• 对于图中的二叉树,后序遍历的结点值打印次序为:

4.层序遍历(二叉树非递归遍历算法)

层序遍历概念:

• 二叉树的层序遍历是借助结点指针队列循环实现的二叉树遍历算法

• 树结点的遍历次序是从低层到高层,同一层从左到右进行遍历的:

层序遍历算法实现思路: 

• 创建一个队列,将树的根结点地址插入队列中；(队列中的数据先进先出,数据从队尾入队从队头出队)
• 接着开始执行循环语句
• 每一次循环,取出队头的一个指针,对其进行处理(打印数值等等处理),若队头指针不为空指针,则将队头指针指向的结点的左右孩子指针插入队列中,重复循环直到队列为空为止.
• 树结点指针入队次序图示:
• 经过分析可知:队列中的树结点地址就是按照树结点的层序逻辑顺序进行排列的(从根结点开始,前一层结点指针出队后会带入下一层结点的指针),因此该算法可以完成二叉树的层序遍历
• 算法gif图示:

层序遍历代码实现:

• 为了方便我们直接使用C++STL的queue类模板 (VS2022的queue对象数据入队(尾插)接口为push,数据出队(头删)接口为pop)(不同编译器接口命名可能不同)
• 如果要使用C语言则需要自己手动实现队列

void LevelOrder(BTNode* root)
{
	queue<BTNode*> NodeStore;			//创建一个队列用于存储结点指针
	NodeStore.push(root);				//将根结点指针插入队列中

	while (!NodeStore.empty())			//若队列不为空则循环继续
	{
		BTNode* tem = NodeStore.front();//保存队头指针
		NodeStore.pop();				//队头指针出队
		if (nullptr != tem)
		{
			cout << (tem->data)<<' ';	//处理出队的结点(这里是打印其结点值)
		}
		if (nullptr != tem)				//若出队结点不为空,则将其孩子结点指针带入队列
		{
			NodeStore.push(tem->left);  //将出队结点的左孩子指针带入队列
			NodeStore.push(tem->right); //将出队结点的右孩子指针带入队列
		}
	}
	cout << endl;
}

三.链式二叉树遍历算法的运用

1.前序遍历算法的运用

前序遍历递归:

1. 先处理根
2. 向左子树递归
3. 向右子树递归

• 由于根处理语句在前序递归函数中是首先执行的,因此我们可以利用前序遍历递归框架来实现链式二叉树的递归构建(在前序递归的框架下我们可以实现先创建根结点,再创建根结点的左右子树,中序和后序递归无法完成树的递归构建)

相关练习: 

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking(本题源自清华大学OJ)

问题描述:

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。

例如:先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

(输入的字符串，长度不超过100.)

示例:

• 输入:abc##de#g##f###
• c b e g d f a 

问题分析:

• 以字符串"abc##de#g##f###"为例,先分析一下在先序遍历的逻辑顺序下该字符串所对应的二叉树结构:如果按照中序逻辑顺序打印这颗树结果为:c-->b-->e-->g-->d-->f-->a;下面给出各个#所代表的空树在树中的逻辑位置:
• 递归构建分析:
• 进一步分析可知:给定的字符串序列必须满足二叉树的前序序列逻辑,不然该字符串序列便无法被转换成一颗完整的二叉树
• 借助递归分析我们可以实现二叉树的递归构建代码

1. 为了方便理解, 先给出主函数测试代码,熟悉递归函数的调用方式:

   int main() 
   {
       char arr[101] = {0};
       scanf("%s",arr);                        //输入待转换的字符串
       int ptr = 0;                            //用于遍历字符串的下标变量
       TreeNode * root = CreateTree(arr,&ptr); //调用建树函数
       InOrder(root);                          //对树进行中序遍历
     
       return 0;
   }

2. 建树递归函数首部:

   TreeNode * CreateTree(char * input,int* ptr)

• input是待转换的字符串的首地址

• ptr是用于遍历字符串的下标变量的地址,这里一定要传址,因为我们要在不同的函数栈帧中修改同一个字符数组下标变量

• 函数实现:

  TreeNode * CreateTree(char * input,int* ptr)
  {
      if('#'==input[*ptr])            //#代表空树,直接将空指针返回给上层结点即可
      {
          ++*ptr;
          return nullptr;
      }
      TreeNode * root = new TreeNode;     //申请新结点
      root->word = input[*ptr];           //结点赋值 
      ++*ptr;                             //字符数组下标加一处理下一个字符
      root->left = CreateTree(input,ptr); //向左子树递归
      root->right = CreateTree(input,ptr);//向右子树递归
      return root;                        //将本层结点地址返回给上一层结点(或返回给根指针变量)
  }

• 整体题解代码:

  #include <iostream>
  #include <string>
  using namespace std;
  
  
  struct TreeNode  //树结点结构体
  {
      char word;
      TreeNode * left;
      TreeNode * right;
  };
  
  //ptr是字符串数组下标的地址,这里一定要传址,因为我们要在不同的函数栈帧中修改同一个字符数组下标变量
  TreeNode * CreateTree(char * input,int* ptr)
  {
      if('#'==input[*ptr])            //#代表空树,直接将空指针返回给上层结点即可
      {
          ++*ptr;
          return nullptr;
      }
      TreeNode * root = new TreeNode;     //申请新结点
      root->word = input[*ptr];           //结点赋值 
      ++*ptr;                             //字符数组下标加一处理下一个字符
      root->left = CreateTree(input,ptr); //向左子树递归
      root->right = CreateTree(input,ptr);//向右子树递归
      return root;                        //将本层
  }
  
  void InOrder(TreeNode * root)           //中序遍历递归
  {
      if(nullptr == root)
      {
          return;
      }
      InOrder(root->left);
      printf("%c ",root->word);
      InOrder(root->right);
  }
  
  int main() 
  {
      char arr[101] = {0};
      scanf("%s",arr);
      int ptr = 0;
      TreeNode * root = CreateTree(arr,&ptr);
      InOrder(root);
    
      return 0;
  }

  

2.后序遍历算法的运用

后序遍历算法:

1. 先向左子树递归
2. 再向右子树递归
3. 完成左右子树的处理后再处理根

后序遍历算法的思想刚好可以适用于二叉树的销毁过程. (前序和中序算法不能完成二叉树的销毁,因为一旦我们释放了当前结点便无法再向左右子树进行递归(地址丢失))

• 二叉树销毁接口:

  // 二叉树销毁
  void BinaryTreeDestory(BTNode* root)
  {
  	if (NULL == root)
  	{
  		return;
  	}
  	BinaryTreeDestory(root->left);
  	BinaryTreeDestory(root->right);
  	free(root);						//释放到当前结点的内存空间
  
  }

• 二叉树销毁过程图示:

3.层序遍历算法的运用

层序遍历算法可以用于检验一颗二叉树是否为完全二叉树;

问题来源:

958. 二叉树的完全性检验 - 力扣（Leetcode）https://leetcode.cn/problems/check-completeness-of-a-binary-tree/问题描述:

给定一个二叉树的 root ,确定它是否是一个完全二叉树 。

在一个 完全二叉树中，除了树的最后一层以外，其他层是完全被填满的，并且最后一层中的所有结点都是靠左排列的。

958. 二叉树的完全性检验 - 力扣（Leetcode）

题解接口:

class Solution 
{
public:
    bool isCompleteTree(TreeNode* root) 
    {

    }
};

 关于完全二叉树的结构特点参见青菜的博客:http://t.csdn.cn/6qErohttp://t.csdn.cn/6qEro

问题分析:

• 完全二叉树的结构特点是各层结点连续排列(各结点编号是连续的)
• 因此层序遍历完全二叉树,各结点指针在队列中都是连续排列的(即各结点指针之间不会出现空指针)
• 根据完全二叉树的结构特点,一旦层序遍历完全二叉树的过程中遍历到了空指针,则说明已经遍历到了二叉树的最后一层
• 我们可以利用层序遍历算法遍历二叉树,当遇到第一个出队的空指针时,检验后续出队的指针中是否还存在非空结点指针,如果后续出队的指针中存在非空指针则说明该树不是完全二叉树,否则说明该树是一颗完全二叉树。
• 算法图示:

 

题解代码: 

class Solution 
{
public:
    bool isCompleteTree(TreeNode* root) 
    {
        queue<TreeNode*> ans;
        ans.push(root);        //将根结点指针插入队列
        while(!ans.empty())    //队列不为空则循环继续
        {
            TreeNode* tem = ans.front();
            ans.pop();         //取出队头指针存入tem变量中
            if(nullptr == tem) //遇到第一个出队的空指针,停止循环进行下一步判断
            {
                break;
            }
            else
            {
                ans.push(tem->left);   //将出队指针的孩子结点指针带入队列
                ans.push(tem->right);
            }
        }
        while(!ans.empty())
        {
            TreeNode* tem = ans.front();
            ans.pop();         //取出队头指针存入tem变量中
            if(nullptr != tem) //第一个出队的空指针后续存在非空结点指针,说明该树不是完全二叉树
            {
                return false;
            }
        }
        return true;           //所有结点指针完成入队出队则验证了该树是完全二叉树
    }
};

 

四.链式二叉树其他操作接口的实现

链式二叉树的众多递归接口都是通过左右子树分治递归的思想来实现的

 树结点结构体定义:

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;                //数据域
	struct BinaryTreeNode* left;    //指向结点左孩子的指针
	struct BinaryTreeNode* right;   //指向结点右孩子的指针
}BTNode;

1. 计算二叉树结点个数的接口

函数首部:

int BinaryTreeSize(BTNode* root)

• 将接口函数抽象为某颗树的结点个数A(T)
• 抽象出递推公式: A(T) = A(T->right) + A(T->left) + 1;
• 递推公式的含义是: 树T的结点总个数 = 树T左子树的结点总个数 + 树T右子树的结点总个数 + 1个树T的树根(本质上是左右子树分治思想)
• 由此可以设计出递归函数:

  int BinaryTreeSize(BTNode* root)
  {
  	//空树则返回0
  	if (NULL == root)
  	{
  		return 0;
  	}
  
  	//化为子问题进行分治
  	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
  }
  

  将下图中的树的根结点地址传入递归函数:

  递归函数执行过程的简单图示: 

   

2.计算二叉树叶子结点的个数的接口

函数首部:

int BinaryTreeLeafSize(BTNode* root)

• 将接口函数抽象为某颗树的叶子结点的个数A(T)
• 可以抽象出递推公式:A(T) = A(T->left) + A(T->right)
• 递推公式的含义是: 树T的叶子总数 = T的左子树的叶子总数 + T的右子树的叶子总数
• 由此可以设计出递归函数:

  int BinaryTreeLeafSize(BTNode* root)
  {
  	if (NULL == root)                                      //空树不计入个数
  	{
  		return 0;
  	}
  	else if (NULL == root->left && NULL == root->right)   //判断当前树是否为树叶(是树叶则返回1,计入叶子结点个数)
  	{
  		return 1;
  	}
  	//化为子问题进行分治
  	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
  }

  将下图中的树的根结点地址传入递归函数:

   递归函数执行过程的简单图示: 

3.计算二叉树第k层结点个数的接口

函数首部:

int BinaryTreeLevelKSize(BTNode* root, int k)

• 将接口函数抽象为某颗树的第k层结点个数A(T,k)
• 可以抽象出递推公式: A(T,k) = A(T->left,k-1) + A(T->right,k-1)
• 递推公式的含义是: 树T的第k层结点个数 = 树T左子树的第k-1层结点数 + 树T右子树的第k-1层结点数
• 由此可以设计出递归函数:

  int BinaryTreeLevelKSize(BTNode* root, int k)
  {
  	assert(k >= 1);
  	//树为空返回0
  	if (NULL == root)
  	{
  		return 0;
  	}
  	else if (root && k == 1)	//问题分解到求子树的第一层结点(即求树根的个数,树根的个数为1)
  	{
  		return 1;
  	}
  	else
  	{
  		return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
  	}
  }

  将下图中的树的根结点地址传入递归函数:

  递归函数执行过程的简单图示: 

   

4.二叉树的结点查找接口(在二叉树中查找值为x的结点)

 函数首部:

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)

递归的思路:

• 若当前树不为空树(若为空树则直接返回空指针),先判断树根是不是要找的结点
• 若树根不是要找的结点,则往左子树递归查找
• 若左子树找不到最后再往右子树递归查找
• 若最后左右子树中都找不到待找结点则返回空指针
• 设计递归函数:

  BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
  {
  	//寻找到空树则返回空(说明在某条连通路径上不存在待找结点)
  	if (NULL == root)
  	{
  		return NULL;
  	}
  	//判断树根是否为待找结点,若判断为真则返回该结点地址
  	else if (root->data == x)
  	{
  		return root;
  	}
  	//若树根不是要找的结点, 则往左子树找
  	BTNode* leftret = BinaryTreeFind(root->left, x);
  	if (leftret)
  	{
  		return leftret;
  	}
  	//若左子树中不存在待找结点,则往右子树找
  	BTNode* rightret = BinaryTreeFind(root->right, x);
  	if (rightret)
  	{
  		return rightret;
  	}
  	//若左右子树中都找不到则说明不存在待找结点,返回空
  	return NULL;
  }
  

  将下图中的树的根结点地址传入递归函数:

  递归函数执行过程的简单图示: 

分治递归的思想是核心哦!!!! 

文章来源地址https://www.toymoban.com/news/detail-783995.html

到了这里，关于数据结构:链式二叉树初阶的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！