注:本博文为本人阅读论文、文章后的原创笔记,未经授权不允许任何转载或商用行为,否则一经发现本人保留追责权利。有问题可留言联系,欢迎指摘批评,共同进步!!!
1. 前言
假设矩阵
A
\mathbf{A}
A是一个
M
×
N
M \times N
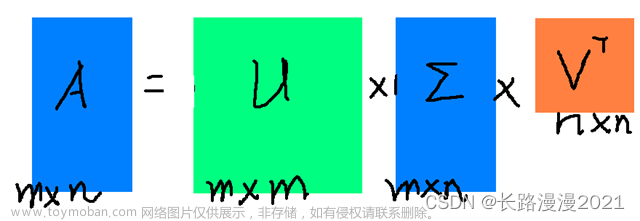
M×N大小的矩阵。对其进行奇异值分解后可以得到:
A
(
m
×
n
)
=
U
(
m
×
m
)
Σ
(
m
×
n
)
V
(
n
×
n
)
T
\mathbf{A_{(m \times n)} = U_{(m \times m)} \Sigma_{(m \times n)} V^T_{(n \times n)}}
A(m×n)=U(m×m)Σ(m×n)V(n×n)T
其中矩阵
Σ
\mathbf{\Sigma}
Σ是准对角矩阵,其对角元素就是奇异值。矩阵
U
\mathbf{U}
U和
V
\mathbf{V}
V都是酉矩阵,一条重要的性质就是,其列向量都是两两正交的单位向量(模为1,对应相乘等于0).
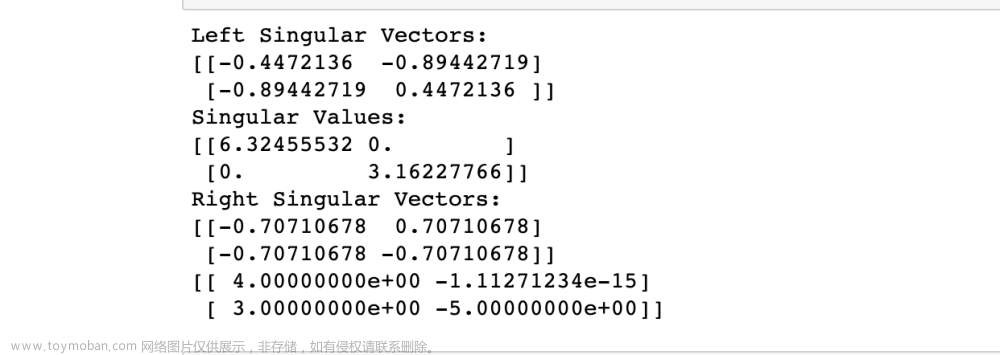
2. 数值计算
在计算时,首先我们考虑计算矩阵 V \mathbf{V} V和准对角阵 Σ : \mathbf{\Sigma}: Σ:
- 首先计算 A T A \mathbf{A^TA} ATA,因为已知矩阵 A \mathbf{A} A大小为 M × N M \times N M×N,因此 A T A \mathbf{A^TA} ATA是大小为 N × N N \times N N×N的方阵,可以进行特征分解,求得 N N N个特征值 λ i ( i = 1 , . . . , N ) \lambda_i(i = 1, ..., N) λi(i=1,...,N)和单位化的特征向量 α i ( i = 1 , . . . , N ) \bm{\alpha_i}(i = 1, ..., N) αi(i=1,...,N).
- 因此,矩阵
V
\mathbf{V}
V和准对角阵
Σ
\mathbf{\Sigma}
Σ可以得到为:
V = ( α 1 α 2 ⋯ α N ) Σ = ( λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ λ N ) \begin{aligned} \mathbf{V} &= (\bm{\alpha_1\ \alpha_2\ \cdots\ \alpha_N}) \\ \mathbf{\Sigma} &= \begin{pmatrix} \sqrt{\lambda_1} & 0 & \cdots & 0\\ 0 & \sqrt{\lambda_2} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \sqrt{\lambda_N} \end{pmatrix} \end{aligned} VΣ=(α1 α2 ⋯ αN)=⎝ ⎛λ10⋮00λ2⋮0⋯⋯⋱⋯00⋮λN⎠ ⎞
注意:矩阵 Σ \mathbf{\Sigma} Σ不一定是方阵,但是也是只有主对角线上有值,其余填0即可;
另外,矩阵 Σ \mathbf{\Sigma} Σ和矩阵 V \mathbf{V} V中的元素一定要以特征值-特征向量对应书写,顺序不可错乱。
计算矩阵 U \mathbf{U} U:
- 计算 A A T \mathbf{AA^T} AAT,因为已知矩阵 A \mathbf{A} A大小为 M × N M \times N M×N,因此 A A T \mathbf{AA^T} AAT是大小为 M × M M \times M M×M的方阵,可以进行特征分解,求得 M M M个特征值 γ i ( i = 1 , . . . , M ) \gamma_i(i = 1, ..., M) γi(i=1,...,M)和单位化的特征向量 θ i ( i = 1 , . . . , M ) \bm{\theta_i}(i = 1, ..., M) θi(i=1,...,M). 由此,我们可以确定,矩阵 U \mathbf{U} U是由 M M M个单位特征向量组成的,但是向量的排列顺序还不确定,接下来就是要确定这件事;
∵ V 是正交矩阵 ∴ V T = V − 1 ⇒ A = U Σ V − 1 ⇒ A V = U Σ \begin{aligned} \because \mathbf{V}是正交矩阵 \\ \therefore \mathbf{V^T} = \mathbf{V^{-1}} \\ \Rightarrow \mathbf{A} = \mathbf{U \Sigma V^{-1}}\\ \Rightarrow \mathbf{AV} = \mathbf{U \Sigma} \end{aligned} ∵V是正交矩阵∴VT=V−1⇒A=UΣV−1⇒AV=UΣ
- 计算出矩阵 A V \mathbf{AV} AV,再由于矩阵 Σ \mathbf{\Sigma} Σ只有主对角线上有元素,可以根据简单的除法,对应计算出矩阵 U \mathbf{U} U中前几列对应的元素。由此可以确定特征向量在矩阵 U \mathbf{U} U中的对应位置关系,然后写出矩阵 U \mathbf{U} U.
- A = U Σ V T \mathbf{A = U \Sigma V^{T}} A=UΣVT(一定要记得矩阵 V \mathbf{V} V最后还有个转置运算)
3. 奇异值分解的原理
在上述数值计算过程中有一个问题,就是为什么矩阵 A T A \mathbf{A^TA} ATA的特征向量就组成矩阵 V \mathbf{V} V,特征值组成矩阵 Σ \mathbf{\Sigma} Σ,而矩阵 A A T \mathbf{AA^T} AAT的特征向量组成矩阵 U \mathbf{U} U呢?接下来就解释这个问题:
-
为什么矩阵 A T A \mathbf{A^TA} ATA的特征向量就组成矩阵 V \mathbf{V} V,特征值开根号组成矩阵 Σ \mathbf{\Sigma} Σ?
A = U Σ V T A T = V Σ T U T = V Σ T U − 1 ( 因为 U 是正交阵 ) ⇒ A T A = V Σ T U − 1 U Σ V T = V Σ 2 V − 1 ⇒ ( A T A ) V = V Σ 2 \mathbf{A = U \Sigma V^T}\\ \mathbf{A^T = V \Sigma^T U^T}=\mathbf{V \Sigma^T U^{-1}}(因为\mathbf{U}是正交阵)\\ \Rightarrow \mathbf{A^TA} = \mathbf{V \Sigma^T U^{-1} U \Sigma V^T} = \mathbf{V \Sigma^2 V^{-1}}\\ \Rightarrow (\mathbf{A^TA})\mathbf{V} = \mathbf{V \Sigma^2} A=UΣVTAT=VΣTUT=VΣTU−1(因为U是正交阵)⇒ATA=VΣTU−1UΣVT=VΣ2V−1⇒(ATA)V=VΣ2
由此可以看到,矩阵 V \mathbf{V} V中包含的列向量实际上就是矩阵 ( A T A ) (\mathbf{A^TA}) (ATA)的特征向量,而矩阵 Σ \mathbf{\Sigma} Σ中的对角值,就是矩阵 ( A T A ) (\mathbf{A^TA}) (ATA)的 特征值 \sqrt{特征值} 特征值. -
为什么矩阵 A A T \mathbf{AA^T} AAT的特征向量组成矩阵 U \mathbf{U} U呢?
显然,这个问题和上面同理。
4. 例题


5. 奇异值分解的几何含义
5.1 数据的线性变换——拉伸
例如,有一组数据
D
\mathbf{D}
D,
D
\mathbf{D}
D表示为如下的矩阵:
D
=
[
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
]
\mathbf{D} = \begin{bmatrix} x_1 & x_2 & x_3 & x_4\\ y_1 & y_2 & y_3 & y_4 \end{bmatrix}
D=[x1y1x2y2x3y3x4y4]
有一矩阵
S
=
[
2
0
0
1
]
\mathbf{S}=\begin{bmatrix} 2 & 0\\ 0 & 1 \end{bmatrix}
S=[2001]作用在该数据矩阵
D
\mathbf{D}
D上,可以得到:
S
D
=
[
2
0
0
1
]
[
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
]
=
[
2
x
1
2
x
2
2
x
3
2
x
4
y
1
y
2
y
3
y
4
]
\mathbf{SD} = \begin{bmatrix} 2 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 & x_2 & x_3 & x_4\\ y_1 & y_2 & y_3 & y_4 \end{bmatrix}= \begin{bmatrix} 2x_1 & 2x_2 & 2x_3 & 2x_4\\ y_1 & y_2 & y_3 & y_4 \end{bmatrix}
SD=[2001][x1y1x2y2x3y3x4y4]=[2x1y12x2y22x3y32x4y4]
这是矩阵运算中一条重要的性质:矩阵 S \mathbf{S} S是由 2 × 2 2 \times 2 2×2大小单位矩阵经由初等变化而来的,当数据矩阵 D \mathbf{D} D左乘上一个单位矩阵的初等变换等于对 D \mathbf{D} D进行对应的行变换。
- 矩阵 D \mathbf{D} D左乘一个 S \mathbf{S} S相当于将基底由默认的 [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [10]和 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01]换为了 [ 2 0 ] \begin{bmatrix} 2\\ 0 \end{bmatrix} [20]和 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01](即矩阵 S \mathbf{S} S的列向量),所以数据进行了拉伸。
5.2 数据的线性变换——旋转
换作一矩阵
R
=
[
c
o
s
(
θ
)
−
s
i
n
(
θ
)
s
i
n
(
θ
)
c
o
s
(
θ
)
]
\mathbf{R} = \begin{bmatrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{bmatrix}
R=[cos(θ)sin(θ)−sin(θ)cos(θ)] 作用与数据矩阵
D
\mathbf{D}
D上(
D
\mathbf{D}
D左乘
R
\mathbf{R}
R),可得:
R
D
=
[
c
o
s
(
θ
)
−
s
i
n
(
θ
)
s
i
n
(
θ
)
c
o
s
(
θ
)
]
[
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
]
\mathbf{RD} = \begin{bmatrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} x_1 & x_2 & x_3 & x_4\\ y_1 & y_2 & y_3 & y_4 \end{bmatrix}
RD=[cos(θ)sin(θ)−sin(θ)cos(θ)][x1y1x2y2x3y3x4y4]
- 同理,矩阵 D \mathbf{D} D左乘一个 R \mathbf{R} R相当于将基底由默认的 [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [10]和 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01]换为了 [ c o s ( θ ) s i n ( θ ) ] \begin{bmatrix} cos(\theta)\\ sin(\theta) \end{bmatrix} [cos(θ)sin(θ)]和 [ − s i n ( θ ) c o s ( θ ) ] \begin{bmatrix} -sin(\theta)\\ cos(\theta) \end{bmatrix} [−sin(θ)cos(θ)](即矩阵 R \mathbf{R} R的列向量),显然与原基底相比,作用后的基底逆时针旋转了 θ \theta θ角度。相应地,数据点也是逆时针旋转 θ \theta θ角度。
5.3 奇异值分解的几何意义
观察矩阵奇异值分解的形式:
A
(
m
×
n
)
=
U
(
m
×
m
)
Σ
(
m
×
n
)
V
(
n
×
n
)
T
\mathbf{A_{(m \times n)} = U_{(m \times m)} \Sigma_{(m \times n)} V^T_{(n \times n)}}
A(m×n)=U(m×m)Σ(m×n)V(n×n)T
由前面的介绍可以知道,矩阵
U
\mathbf{U}
U和矩阵
V
\mathbf{V}
V都是酉矩阵。而酉矩阵有如下性质:
若矩阵 A \mathbf{A} A为酉矩阵,则
- 性质1: A H A = E \mathbf{A^HA=E} AHA=E 且 A A H = E \mathbf{AA^H=E} AAH=E,即表明酉矩阵行与行、列与列之间都是正交的,且各行、各列都是单位向量;
- 性质2: A H = A − 1 \mathbf{A^H=A^{-1}} AH=A−1且共轭转置矩阵和逆矩阵也都是酉矩阵
因此矩阵 U \mathbf{U} U和矩阵 V T \mathbf{V^T} VT的每一列都是单位向量,且列与列之间相互正交,可以代表旋转变换的基底;矩阵 Σ \mathbf{\Sigma} Σ只有主对角线上有 元素,可以代表拉伸(或收缩)变换的基底。
实际上,单位正交矩阵就可以看做是一组旋转变换的基底;对角矩阵可以看做是拉伸变换的基底。
因此,但任意的矩阵 A \mathbf{A} A作用于数据矩阵时,相当于将数据坐标点先进行旋转变换,再进行拉伸变换,最后再进行一次旋转变换。对于任意一个给定的变换 A \mathbf{A} A,都可以拆解成一个旋转、伸缩、再旋转的变换。奇异值本身的数值,代表了单位超球体经变换后成为的超椭球体的每条半轴的长度。
6. 奇异值分解的应用价值
假设矩阵
A
\mathbf{A}
A的奇异值分解为:
A
(
m
×
n
)
=
U
(
m
×
m
)
Σ
(
m
×
n
)
V
(
n
×
n
)
T
=
[
u
1
u
2
⋯
u
m
]
[
λ
1
1
2
λ
2
1
2
⋯
]
[
v
1
T
v
2
T
⋮
v
n
T
]
\begin{aligned} \mathbf{A_{(m \times n)}} &= \mathbf{U_{(m \times m)} \Sigma_{(m \times n)} V^T_{(n \times n)}}\\ &= \begin{bmatrix} \mathbf{u_1} & \mathbf{u_2} & \cdots & \mathbf{u_m} \end{bmatrix} \begin{bmatrix} \lambda_1^{\frac{1}{2}} & & \\ & \lambda_2^{\frac{1}{2}} & \\ & & \cdots \end{bmatrix} \begin{bmatrix} \mathbf{v^T_1}\\ \mathbf{v^T_2}\\ \vdots \\ \mathbf{v^T_n} \end{bmatrix} \end{aligned}
A(m×n)=U(m×m)Σ(m×n)V(n×n)T=[u1u2⋯um]⎣
⎡λ121λ221⋯⎦
⎤⎣
⎡v1Tv2T⋮vnT⎦
⎤
此处
u
i
\mathbf{u_i}
ui和
v
i
\mathbf{v_i}
vi均为列向量(秩一矩阵),
Σ
\mathbf{\Sigma}
Σ矩阵中存储的奇异值
λ
i
1
2
\lambda^{\frac{1}{2}}_i
λi21按照由大到小的顺序对角排列:
λ
1
>
λ
2
>
⋯
>
λ
m
i
n
(
m
×
n
)
\lambda_1 > \lambda_2 > \cdots > \lambda_{min(m \times n)}
λ1>λ2>⋯>λmin(m×n)。
如下图运算步骤所示,我们实际上可以将矩阵
A
\mathbf{A}
A的奇异值分解再写为众多的秩一矩阵积的和的形式:
即,矩阵
A
=
σ
1
u
1
v
1
T
+
σ
2
u
2
v
2
T
+
⋯
+
σ
r
u
r
v
r
T
\mathbf{A}=\sigma_1\mathbf{u_1}\mathbf{v^T_1}+\sigma_2\mathbf{u_2}\mathbf{v^T_2}+\cdots+\sigma_r\mathbf{u_r}\mathbf{v^T_r}
A=σ1u1v1T+σ2u2v2T+⋯+σrurvrT(r表示矩阵
Σ
\mathbf{\Sigma}
Σ的秩)。奇异值往往代表着矩阵中隐含信息的重要程度,奇异值越大,信息越重要。因此,可以根据奇异值分解来进行数据压缩。例如,矩阵
A
\mathbf{A}
A代表一张高清图片,但是碍于存储大小的限制,需要对图片进行压缩,那么我们就可以对图像矩阵
A
\mathbf{A}
A进行奇异值分解,然后仅保留分解后奇异值大的
k
k
k(
k
<
<
r
k << r
k<<r)个部分,构成一个新的图片矩阵
A
′
\mathbf{A'}
A′即:
A
′
=
σ
1
u
1
v
1
T
+
⋯
+
σ
k
u
k
v
k
T
\mathbf{A'}=\sigma_1\mathbf{u_1}\mathbf{v^T_1}+\cdots+\sigma_k\mathbf{u_k}\mathbf{v^T_k}
A′=σ1u1v1T+⋯+σkukvkT。此时即完成了对图片的压缩。文章来源:https://www.toymoban.com/news/detail-784050.html
有趣的性质:
由于矩阵 U \mathbf{U} U和 V \mathbf{V} V都是满秩的,所以原矩阵 A \mathbf{A} A和对角阵 Σ \mathbf{\Sigma} Σ的秩相同,因此,想要求原矩阵 A \mathbf{A} A的秩,那么只要对A进行奇异值分解,然后数一数奇异值的个数就可以了。文章来源地址https://www.toymoban.com/news/detail-784050.html
7. 相关资料
- 相关讲解视频:
1. 矩阵的【奇异值分解】(SVD),图像压缩
2. 【学长小课堂】什么是奇异值分解SVD–SVD如何分解时空矩阵 - 相关讲解内容专栏:
知乎回答
到了这里,关于矩阵的奇异值分解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!