C/C++数据结构（十一）—— 平衡二叉树（AVL树）

1. AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

因此，两位俄罗斯的数学家 G.M.Adelson-Velskii 和 E.M.Landis 在 1962 年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过 1（需要对树中的结点进行调整），即可降低树的高度，从而减少平均搜索长度。

平衡二叉树（Balanced Binary Tree 或 Height-Balanced Tree）又称为 AVL 树，其实就是一颗 平衡的二叉排序树 ，解决了二叉查找树的不平衡问题，即斜树。

AVL树或者是一颗空树，或者是具有下列性质的二叉搜索树：

• 它的左子树和右子树都是平衡二叉树
• 左右子树高度之差（简称平衡因子）的绝对值不超过 1（即：-1，0，1）

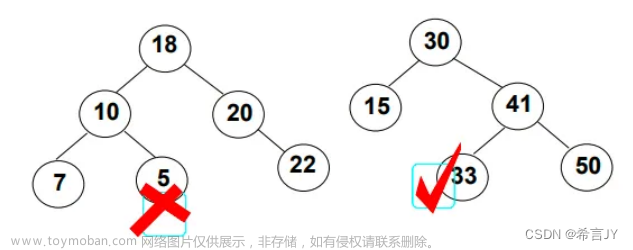
举个例子，下图就是一颗典型的 AVL 树，每个节点旁边都标注了平衡因子：

上面是一颗典型的平衡二叉树，首先它是一颗二叉排序树，其次每一个结点的平衡因子都是 -1，0，1 三个数当中的一个。

红色的数字为结点的平衡因子，对于任意一个叶子结点而言，其左右孩子都为空，左子树的深度为 0 ，右子树的深度为 0 ，所以 AVL树当中的叶子结点的平衡因子都是 0 ；

其他结点的平衡因子同样通过 右子树深度减去左子树深度 可以求得，比如结点 3 的 左子树深度为 2，右子树深度为1 ，则平衡因子为 $1-2=-1$。

如果一棵二叉搜索树是高度平衡的，它就是 AVL 树。如果它有 n 个结点，其高度可保持在 $O(logn)$，搜索时间复杂度 $O(logn$)。

再来看看不平衡的情况，如下面这颗树：

上图中就是不平衡的二叉排序树，非 AVL树 。结点 5 的平衡因子为 -2，该平衡因子是结点 5 右子树深度 2 减去左子树深度 4 所得；

我们要学习的就是将这种不平衡的二叉搜索树转化为 AVL树。

2. AVL树的结点

我们直接按照 KV 模型来构造 AVL 树，需要把结点定义为 三叉链结构，并在每个结点当中引入平衡因子（右子树高度-左子树高度）。

对于结点的构造函数，由于新构造结点的左右子树均为空树，所以只需要将新构造结点的平衡因子初始设置为 0 即可。

代码示例

template<class K, class V>
struct AVLTreeNode
{
	// 存储的键值对
	pair<K, V> _kv;

	// 三叉链
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;

	// 平衡因子(balance factor)
	int _bf; // 右子树高度 - 左子树高度

	// 构造函数
	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_bf(0)
	{}
};

3. AVL树的插入

对平衡二叉树的插入操作而言，其本质上比二叉搜索树的插入操作多了一个平衡操作，解决了二叉搜索树插入操作可能出现的斜树，不平衡问题。

那么 AVL 树的插入过程可以分为两步：

• 按照二叉搜索树的方式，找到待插入的位置，然后将新结点插入到该位置。
• 调整节点的平衡因子，如果出现不平衡，则需要进行旋转。

🍑 更新平衡因子

当 AVL 树插入一个新结点以后，需要更新插入结点的祖先的平衡因子，因为新结点（也就是叶子结点）的平衡因子为 0，但是它影响的是它的父亲，它父亲的父亲…，所以要更新到祖先结点。

所以我们要从新增结点开始，往上沿着祖先路径更新，那么更新的规则如下：

• 如果新增结点插入在 parent 的右边，只需要给 parent 的平衡因子 +1 即可
• 如果新增结点插入在 parent 的左边，只需要给 parent 的平衡因子 -1 即可

为什么呢？因为平衡因子的计算方法是：右子树高度 - 左子树高度，如果插入在右边，那么最后的结果肯定是要 ++，反之，则 --。

当 parent 的平衡因子更新完以后，可能出现三种情况：0，正负 1，正负 2。

（1）parent 的平衡因子为 0

如果 parent 的平衡因子为 0，说明插入之前 parent 的平衡因子为正负 1，插入后被调整成 0，此时满足 AVL 树的性质，则插入成功。

如下图所示，插入后使得 parent 左右子树的高度相等了，此操作并没有改变以 parent 为根结点的子树的高度，从而不会影响 parent 的父结点的平衡因子，因此无需继续往上更新平衡因子。

（2）如果 parent 的平衡因子为正负 1

如果 parent 的平衡因子为正负 1，说明插入前 parent 的平衡因子一定为 0，插入后被更新成正负 1。

如下图所示，当新增一个结点以后，parent 的平衡因子从 0 变成了 1，说明新结点的插入使得 parent 的右子树增高了，即改变了以 parent 为根结点的子树的高度，从而会影响 parent 的父结点的平衡因子，因此需要继续往上更新平衡因子。

如下图所示，当新增一个结点以后，parent 的平衡因子从 0 变成了 -1，说明新结点的插入使得 parent 的左子树增高了，即改变了以 parent 为根结点的子树的高度，从而会影响 parent 的父结点的平衡因子，因此需要继续往上更新平衡因子。

进而引出了下面的第 3 种情况。

（3）如果 parent 的平衡因子为正负 2

如果 parent 的平衡因子为 -2，此时 parent 结点的左右子树高度之差的绝对值已经超过 1 了，则 parent 的平衡因子违反平衡树的性质，那么就停止更新，需要对其进行旋转处。

如果 parent 的平衡因子为 2，此时 parent 结点的左右子树高度之差的绝对值已经超过 1 了，则 parent 的平衡因子违反平衡树的性质，那么就停止更新，需要对其进行旋转处。

可以看到，当 parent 的平衡因子为正负 2 时，cur 的平衡因子必定是正负 1 而不会是 0。

🍑 插入函数的实现

上面我们分析了，如果在更新平衡因子的过程当中，出现了平衡因子为正负 2 的结点，此时需要对 以该结点为根结点的树 进行旋转处理（待会儿再讲旋转）。

我们定义一个 cur 用来表示 新增结点，定义一个 parent 用来表示 新增结点的父亲结点。

那么我们更新平衡因子时，第一个要更新的就是 parent 结点的平衡因子，更新完 parent 结点的平衡因子后，若是需要继续往上进行平衡因子的更新，那么要执行以下操作：

if (parent->_bf == 1 || parent->_bf == -1)
{
	cur = cur->_parent; // cur指向了它的父亲
	parent = parent->_parent; // 它的父亲指向了它的祖先
}

可以看到，我们之所以将 AVL 树结点的结构设置为三叉链结构，是因为我们可以很方便的通过父指针找到其父结点，进而对其平衡因子进行更新。

而当 parent 的平衡因子为正负 2 时，我们需要对其进行旋转操作，当旋转完成以后，就无需继续往上更新平衡因子了，即树的高度没有发生变化，也就不会影响其父结点的平衡因子了。

if (parent->_bf == 2 || parent->_bf == -2)
{
	// 旋转的四种处理方式
	// 1.左单旋
	// 2.右单旋
	// 3.左右双旋
	// 4.右左双旋

	// 当旋转完成以后，直接跳出
	break;
}

代码示例

public:
	// 插入函数
	bool Insert(const pair<K, V>& kv)
	{
		// 如果AVL树是空树，把插入节点直接作为根节点
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_bf = 0;
			return true;
		}

		// 1.按照二叉搜索树的规则插入
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first) // 待插入节点的key值大于当前节点的key值
			{
				// 往右子树走
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first) // 待插入节点的key值小于当前节点的key值
			{
				// 往左子树走
				parent = cur; 
				cur = cur->_left;
			}
			else // 待插入节点的key值等于当前节点的key值
			{
				return false; // 插入失败，返回false
			}
		}

		// 2.当循环结束，说明cur找到了空的位置，那么就插入
		cur = new Node(kv); // 构造一个新节点
		if (parent->_kv.first < kv.first) // 如果新节点的key值大于当前parent节点的key值
		{
			// 就把新节点链接到parent的右边
			parent->_right = cur;
		}
		else // 如果新节点的key值小于当前parent节点的key值
		{
			// 就把新节点链接到parent的左边
			parent->_left = cur;
		}
		cur->_parent = parent; // 别忘了把新节点里面的_parent指向parent(因为我们定义的是一个三叉链)

		// 3.更新平衡因子,如果出现不平衡,则需要进行旋转
		while (parent) // 最远要更新到根节点去
		{
			if (cur == parent->_right) // 如果cur插在parent的右边，说明parent的右子树增高
			{
				parent->_bf++; // 那么parent的平衡因子要++
			}
			else // 如果cur插在parent的左边，说明parent的左子树增高
			{
				parent->_bf--; // 那么parent的平衡因子要--
			}

			// 判断是否更新结束，或者是否需要进行旋转
			if (parent->_bf == 0) // 如果parent的bf等于0，说明左右子树高度一致，就更新结束(原因是新插入的节点把parent左右子树中矮的那一边给填补了）
			{
				// 高度不变,更新结束
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1) // 继续往上更新平衡因子(插入节点导致某一边变高了，说明parent所在的子树高度改变了)
			{
				// 子树的高度变了，就要继续往上更新祖先
				cur = cur->_parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2) // 说明插入节点导致本来高的一边又变高了，子树不平衡了，那么此时需要做旋转处理
			{
				// 旋转的四种处理方式
				// 1.左单旋
				// 2.右单旋
				// 3.左右双旋
				// 4.右左双旋
				
				// 旋转完成，跳出
				break;
			}
			else
			{
				// 如果程序走到了这里，说明在插入节点之前AVL树就存在不平衡的子树，也就是存在平衡因子 >= 2的节点
				// 所以这里加一个断言进行处理
				assert(false);
			}
		}
		// 插入成功，返回true
		return true;
	}

4. AVL树的旋转

如果在一棵原本是平衡的 AVL 树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。

根据节点插入位置的不同，AVL 树的旋转分为四种：

• 左单旋（LL）
• 右单旋（RR）
• 左右双旋（LR）
• 右左双旋（RL）

其实我们只要搞懂 LL 和 RR 就好了，因为 LR 和 RL 都是由它们演变而来的。

不管是什么旋转，都必须满足两点原则：

• 保持搜索树的规则
• 子树变平衡

🍑 左单旋

下面是一个 AVL 树的抽象图，长方形条代表的是子树，h 表示 a，b，c 三颗子树的高度。

• 结点 30 的右子树深度为 h + 2，左子树深度为 h + 1，所以平衡因子为 1。
• 结点 60 的右子树深度为 h + 1，左子树深度为 h + 1，所以平衡因子为 0。

现在我们在 c 子树的中插入一个新结点，那么此时 c 子树的高度就变成了 h + 1，同时结点 60 的平衡因子为 1，结点 30 的平衡因子为 2，此时右边的高度大于左边的高度，需要进行左单旋。

左单旋的步骤如下：

• 先让 subR 的左子树（subRL）作为 parent 的右子树。
• 然后让 parent 作为 subR 的左子树。
• 接下来让 subR 作为整个子树的根。
• 最后更新平衡因子。

左单旋图如下所示：

经过旋转以后，它们的平衡因子就发生了变化：

• 结点 30 的右子树深度为 h，左子树深度为 h，所以平衡因子为 0。
• 结点 60 的右子树深度为 h + 1 + 1，左子树深度为 h + 1 + 1，所以平衡因子为 0。

这样旋转以后还满足二叉搜索树的性质吗？当面满足，原因如下：

• subR 的左子树（subRL）当中结点的值本身就比 parent 的值大，因此可以作为 parent 的右子树。
• 而 parent 及其左子树当中结点的值本身就比 subR 的值小，因此可以作为 subR 的左子树。

什么时候需要用到左旋操作呢？可以看到，当 parent 的平衡因子为 2，cur 的平衡因子为 1 时，需要进行左单旋。并且经过左单旋后，树的高度没有发生变化，所以左单旋后无需继续往上更新平衡因子。

左单旋动图演示：

可以看到，我们在 32 的右边插入一个值为 35 的新节点，那么此时 32 的平衡因子从 0 变成了 1，29 的平衡因子从 1 变成了 2，出现了右边高，左边低的局面，所以需要进行左单旋

代码示例

private:
	// 左单旋（右边高需要左单旋）
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* ppNode = parent->_parent; // 先保存parent的parent

		// 1.建立parent和subRL之间的关系
		parent->_right = subRL;
		if (subRL) // 如果subRL节点不为空，那么要更新它的parent
		{
			subRL->_parent = parent;
		}

		// 2.建立subR和parent之间的关系
		subR->_left = parent;
		parent->_parent = subR;

		// 3.建立ppNode和subR之间的关系（分情况讨论parent是整颗树的根，还是局部子树）
		if (parent == _root) // 当parent是根节点时
		{
			_root = subR; // subR就变成了新的根节点
			_root->_parent = nullptr; // 根节点的的parent为空
		}
		else // 当parent是整个树的局部子树时
		{
			if (parent == ppNode->_left) // 如果parent在ppNode的左边
			{
				ppNode->_left = subR; // 那么subR就是parent的左子树
			}
			else // 如果parent在ppNode的右边
			{
				ppNode->_right = subR; // 那么subR就是parent的右子树
			}
			subR->_parent = ppNode; // subR的parent还要指向ppNode
		}

		// 更新平衡因子
		parent->_bf = 0;
		subR->_bf = 0;
	}

还有一点需要注意，如果在旋转前 parent（30） 就是树的根，那么此时只需要更新根结点为 subR（60）即可。

如果 parent（30） 只是整颗树局部的一颗子树，那么此时就需要看 30 是它父亲的左子树还是右子树，然后再和 subR 链接起来，如下图所示：

🍑 右单旋

下面是一个 AVL 树的抽象图，长方形条代表的是子树，h 表示 a，b，c 三颗子树的高度。

• 结点 30 的右子树深度为 h，左子树深度为 h，所以平衡因子为 0。
• 结点 60 的右子树深度为 h + 1，左子树深度为 h + 1 + 1，所以平衡因子为 -1。

现在我们在 a 子树的中插入一个新结点，那么此时 a 子树的高度就变成了 h + 1，同时结点 60 的平衡因子为 -2，结点 30 的平衡因子为 -1，此时左边的高度大于右边的高度，需要进行右单旋。

右单旋的步骤如下：

• 先让 subL 的右子树（subLR）作为 parent 的左子树。
• 然后让 parent 作为 subL 的右子树。
• 接下来让 subL 作为整个子树的根。
• 最后更新平衡因子。

右单旋图如下所示：

经过旋转以后，它们的平衡因子就发生了变化：

• 结点 30 的右子树深度为 h + 1 + 1，左子树深度为 h + 1 + 1，所以平衡因子为 0。
• 结点 60 的右子树深度为 h + 1，左子树深度为 h + 1，所以平衡因子为 0。

这样旋转以后还满足二叉搜索树的性质吗？当面满足，原因如下：

• subL 的右子树当中结点的值本身就比 parent 的值小，因此可以作为 parent 的左子树。
• 而 parent 及其右子树当中结点的值本身就比 subL 的值大，因此可以作为 subL 的右子树。

什么时候需要用到右旋操作呢？可以看到，当 parent 的平衡因子为 -2，cur 的平衡因子为 -1 时，需要进行右单旋。并且经过右单旋后，树的高度没有发生变化，所以右单旋后无需继续往上更新平衡因子。

右单旋动图演示：

可以看到，我们在 9 的左边插入一个值为 5 的新节点，那么此时 9 的平衡因子从 0 变成了 -1，11 的平衡因子从 -1 变成了 -2，出现了左边高，右边低的局面，所以需要进行右单旋

代码示例

private:
	// 右单旋（左边高就右单旋）
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left; 
		Node* subLR = subL->_right;
		Node* ppNode = parent->_parent;

		// 1.建立parent和subLR之间的关系
		parent->_left = subLR;
		if (subLR) // 如果subLR节点不为空，那么要更新它的parent
		{
			subLR->_parent = parent;
		}
		 
		// 2.建立subL和parent之间的关系
		subL->_right = parent;
		parent->_parent = subL;

		// 3.建立ppNode和subL之间的关系（分情况讨论parent是整颗树的根，还是局部子树）
		if (parent == _root) // 当parent是根节点时
		{
			_root = subL; // subL就变成了新的根节点
			_root->_parent = nullptr; // 根节点的的parent为空
		}
		else // 当parent是整个树的局部子树时
		{
			if (parent == ppNode->_left) // 如果parent在ppNode的左边
			{
				ppNode->_left = subL; // 那么subL就是parent的左子树
			}
			else // 如果parent在ppNode的右边
			{
				ppNode->_right = subL; // 那么subL就是parent的右子树
			}
			subL->_parent = ppNode; // subR的parent还要指向ppNode
		}
		// 更新平衡因子
		parent->_bf = 0;
		subL->_bf = 0;
	}

需要注意，如果在旋转前 parent（60） 就是树的根，那么此时只需要更新根结点为 subL（30）即可。

如果 parent（60） 只是整颗树局部的一颗子树，那么此时就需要看 60 是它父亲的左子树还是右子树，然后再和 subL 链接起来。

🍑 左右双旋

下面是一个 AVL 树的抽象图，长方形条代表的是子树，h 表示 a 和 d 两颗子树的高度，h-1 代表 b 和 c 两颗子树的高度。

• 结点 90 的右子树深度为 h + 1，左子树深度为 h + 1 + 1，所以平衡因子为 -1。
• 结点 30 的右子树深度为 h - 1 + 1 + 1，左子树深度为 h + 1，所以平衡因子为 0。
• 结点 60 的右子树深度为 h - 1，左子树深度为 h - 1，所以平衡因子为 0。

现在我们在 b 子树的中插入一个新结点，那么此时 b 子树的高度就变成了 h，同时结点 60 的平衡因子变成了 -1，结点 30 的平衡因子变成了 1，结点 90 的平衡因子变成了 -2，此时如果单纯的以结点 90 为旋转点进行左单旋或者右单旋以后，那么仍然不是 AVL 树，所以需要采取左右双旋的方式。

注意：在 b 子树当中新增结点，或是在 c 子树当中新增结点，均会引发左右双旋，这里以在 b 子树当中新增结点为例。

左右双旋的步骤如下：

• 先以 subL 为旋转点进行左单旋。
• 然后以 parent 为旋转点进行右单旋。
• 最后再更新平衡因子。

（1）以 30 为旋转点进行左单旋

（2）以 90 为旋转点进行右单旋

左右双旋后，实际上就是让 subLR 的左子树和右子树，分别作为 subL 和 parent 的右子树和左子树，再让 subL 和 parent 分别作为 subLR 的左右子树，最后让 subLR 作为整个子树的根

这样旋转以后还满足二叉搜索树的性质吗？当面满足，原因如下：

• subLR 的左子树当中的结点本身就比 subL 的值大，因此可以作为 subL 的右子树。
• subLR 的右子树当中的结点本身就比 parent 的值小，因此可以作为 parent 的左子树。
• 经过步骤1 和 2 以后，subL 及其子树当中结点的值都就比 subLR 的值小，而 parent 及其子树当中结点的值都就比 subLR 的值大，因此它们可以分别作为 subLR 的左右子树。

左右双旋后，平衡因子的更新随着 subLR 原始平衡因子的不同分为以下三种情况：

（1）当 subLR 原始平衡因子是 -1 时，左右双旋后 parent、subL、subLR 的平衡因子分别更新为 1、0、0

（2）当 subLR 原始平衡因子是 1 时，左右双旋后 parent、subL、subLR 的平衡因子分别更新为 0、-1、0

（3）当 subLR 原始平衡因子是 0 时（说明 subLR 为新增结点），左右双旋后 parent、subL、subLR 的平衡因子分别更新为0、0、0

可以看到，经过左右双旋后，树的高度没有发生变化，所以左右双旋后无需继续往上更新平衡因子。

代码示例

private:
// 左右双旋（先左单旋，再右单旋）
	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		// 1.先以subL为旋转点进行左单旋
		RotateL(parent->_left);

		// 2.再以parent为旋转点进行右单旋
		RotateR(parent);

		// 3.更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			// 如果走到了这里，说明subLR的平衡因子在旋转前就有问题
			assert(false);
		}
	}

🍑 右左双旋

下面是一个 AVL 树的抽象图，长方形条代表的是子树，h 表示 a 和 d 两颗子树的高度，h-1 代表 b 和 c 两颗子树的高度。

• 结点 30 的右子树深度为 h + 1 + 1，左子树深度为 h + 1，所以平衡因子为 1。
• 结点 90 的右子树深度为 h + 1，左子树深度为 h - 1 + 1 + 1，所以平衡因子为 0。
• 结点 60 的右子树深度为 h - 1，左子树深度为 h - 1，所以平衡因子为 0。

现在我们在 c 子树的中插入一个新结点，那么此时 c 子树的高度就变成了 h，同时结点 60 的平衡因子变成了 1，结点 00 的平衡因子变成了 -1，结点 30 的平衡因子变成了 -2，此时如果单纯的以结点 30 为旋转点进行左单旋或者右单旋以后，那么仍然不是 AVL 树，所以需要采取右左双旋的方式。

注意：在 b 子树当中新增结点，或是在 c 子树当中新增结点，均会引发右左双旋，这里以在 c 子树当中新增结点为例。

右左双旋的步骤如下：

• 先以 subR 为旋转点进行右单旋。
• 然后以 parent 为旋转点进行左单旋。
• 最后再更新平衡因子。

（1）以 90 为旋转点进行右单旋

（2）以 30 为旋转点进行左单旋

右左双旋后，实际上就是让 subRL 的左子树和右子树，分别作为 parent 和 subR 的右子树和左子树，再让 parent 和 subR 分别作为 subRL 的左右子树，最后让 subRL 作为整个子树的根。

这样旋转以后还满足二叉搜索树的性质吗？当面满足，原因如下：

• subRL 的左子树当中的结点本身就比 parent 的值大，因此可以作为 parent 的右子树。
• subRL 的右子树当中的结点本身就比 subR 的值小，因此可以作为 subR 的左子树。
• 经过步骤 1 和 2 以后，parent 及其子树当中结点的值都就比 subRL 的值小，而 subR 及其子树当中结点的值都就比 subRL 的值大，因此它们可以分别作为 subRL 的左右子树。

右左双旋后，平衡因子的更新随着 subLR 原始平衡因子的不同分为以下三种情况：

（1）当 subRL 原始平衡因子是 1 时，左右双旋后 parent、subR、subRL 的平衡因子分别更新为 -1、0、0

（2）当 subRL 原始平衡因子是 -1 时，左右双旋后 parent、subR、subRL 的平衡因子分别更新为 0、1、0

（3）当 subRL 原始平衡因子是 0 时（说明 subRL为新增结点），左右双旋后 parent、subR、subRL 的平衡因子分别更新为0、0、0

可以看到，经过右左双旋后，树的高度没有发生变化，所以右左双旋后无需继续往上更新平衡因子。

代码示例

private:
	// 右左双旋（先右单旋，再左单旋）
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		// 1.先以subR为旋转点进行右单旋
		RotateR(parent->_right);

		// 2.再以parent为旋转点进行左单旋
		RotateL(parent);

		// 3.更新平衡因子
		if (bf == 0)
		{
			subRL->_bf = 0;
			parent->_bf = 0;
			subR->_bf = 0;
		}
		else if (bf == 1)
		{
			subRL->_bf = 0;
			parent->_bf = -1;
			subR->_bf = 0;
		}
		else if (bf == -1)
		{
			subRL->_bf = 0;
			parent->_bf = 0;
			subR->_bf = 1;
		}
		else
		{
			// 如果走到了这里，说明subRL的平衡因子在旋转前就有问题
			assert(false);
		}
	}

🍑 总结

假如以 parent 为根的子树不平衡，即 parent 的平衡因子为 2 或者 -2，分以下情况考虑

1. parent 的平衡因子为 2，说明 parent 的右子树高，设 parent 的右子树的根为 subR
   • 当 subR 的平衡因子为 1 时，执行左单旋
   • 当 subR 的平衡因子为 -1 时，执行右左双旋
2. parent 的平衡因子为 -2，说明 parent 的左子树高，设 parent 的左子树的根为 subL
   • 当 subL 的平衡因子为 -1 是，执行右单旋
   • 当 subL 的平衡因子为 1 时，执行左右双旋

旋转完成后，原 parent 为根的子树个高度降低，已经平衡，不需要再向上更新。

6. AVL树的删除

平衡二叉树的删除操作与插入操作类似，先执行标准的 BST 删除操作（可以参考文章： 什么是二叉查找树），然后进行相应的平衡操作。

主要是三个大思路：

1. 按二叉搜索树的规则删除
2. 更新平衡因子
3. 出现不平衡，需要旋转调整

只不过与二叉搜索树的删除不同的是，删除节点后的平衡因子需要不断更新，最差情况下一直要调整到根节点的位置。

下面简单讲解一下删除的算法思想吧。

🍑 算法思想

我们以删除一个结点 w 为例进行说明平衡二叉树删除操作的具体算法步骤：

• 对结点 w 执行标准的二叉搜索树的删除操作；
• 从结点 w 开始，向上回溯，找到第一个不平衡的结点 z （即平衡因子不是 -1，0 或 1 的结点），设 y 为结点 z 的高度最高的孩子结点； x 是结点 y 的高度最高的孩子结点。
• 然后对以 z 为根结点的子树进行平衡操作，其中 x、y、z 可以的位置有四种情况，BST 删除操作之后的平衡操作也就处理以下四种情况：
  • y 是 z 的左孩子，x 是 y 的左孩子 （Left Left ，LL )；
  • y 是 z 的左孩子，x 是 y 的右孩子 （Left Right ，LR )；
  • y 是 z 的右孩子，x 是 y 的右孩子 （Right Right ，RR )；
  • y 是 z 的右孩子，x 是 y 的左孩子 （Right Right ，RL )；

这里的四种情况与插入操作一样，但需要注意的是，插入操作仅需要对以 z 为根的子树进行平衡操作；而平衡二叉树的删除操作就不一样，先对以 z 为根的子树进行平衡操作，之后可能需要对 z 的祖先结点进行平衡操作，向上回溯直到根结点。

🍑 示例一

我们已删除下图中的结点 32 为例进行说明。

第一步：由于 32 结点为叶子结点，直接删除，并保存删除结点的父节点 17 。

第二步：从节点 17 向上回溯，找到第一个不平衡结点 44 ，并找到不平衡结点的左右孩子中深度最深的结点 78 （即 y ）；以及 y 的孩子结点当中深度最深的结点 50 （即 x ）。 发现为 RL 的情况。

第三步：对结点 78 进行右旋操作

第四步：对结点 44 进行左旋操作

🍑 示例二

我们以删除下图中的结点 80 为例进行说明。

第一步，由于结点 80 为叶子结点，则直接删除，并保存结点 80 的父结点 78 。

第二步：从结点 78 开始寻找第一个不平衡结点，发现就是结点 78 本身（即结点 z ），找到结点 78 深度最深的叶子结点 60 （即结点 y ），以及结点 y 的深度最深的叶结点 55 （即结点 x ）。即 LL 的情况。

第三步：右旋结点 78

第四步：从旋转后的返回的新的根结点 60 向上回溯（这里就和平衡二叉树的插入操作有别了奥，平衡二叉树的插入操作仅对第一个不平衡结点的子树进行平衡操作，而AVL的删除需要不断地回溯，直到根结点平衡为止 ），判断是否还有不平衡结点，发现整棵树的根结点 50 为第一个不平衡结点，找到对应的 y 结点 25 和 x 结点 10 。同样是 LL 的情况。

第五步：对 z 结点 50 进行右旋操作。

🍑 代码实现

关于左旋与右旋操作，以及平衡因子的计算与之前讲的文章（ 什么是二叉查找树）中的实现是一致的，我们直接看 AVL 树删除操作的实现代码：

代码示例

// 删除函数
	bool Erase(const K& key)
	{
		//用于遍历二叉树
		Node* parent = nullptr;
		Node* cur = _root;
		//用于标记实际的删除结点及其父结点
		Node* delParentPos = nullptr;
		Node* delPos = nullptr;
		while (cur)
		{
			if (key < cur->_kv.first) //所给key值小于当前结点的key值
			{
				//往该结点的左子树走
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_kv.first) //所给key值大于当前结点的key值
			{
				//往该结点的右子树走
				parent = cur;
				cur = cur->_right;
			}
			else //找到了待删除结点
			{
				if (cur->_left == nullptr) //待删除结点的左子树为空
				{
					if (cur == _root) //待删除结点是根结点
					{
						_root = _root->_right; //让根结点的右子树作为新的根结点
						if (_root)
							_root->_parent = nullptr;
						delete cur; //删除原根结点
						return true; //根结点无祖先结点，无需进行平衡因子的更新操作
					}
					else
					{
						delParentPos = parent; //标记实际删除结点的父结点
						delPos = cur; //标记实际删除的结点
					}
					break; //删除结点有祖先结点，需更新平衡因子
				}
				else if (cur->_right == nullptr) //待删除结点的右子树为空
				{
					if (cur == _root) //待删除结点是根结点
					{
						_root = _root->_left; //让根结点的左子树作为新的根结点
						if (_root)
							_root->_parent = nullptr;
						delete cur; //删除原根结点
						return true; //根结点无祖先结点，无需进行平衡因子的更新操作
					}
					else
					{
						delParentPos = parent; //标记实际删除结点的父结点
						delPos = cur; //标记实际删除的结点
					}
					break; //删除结点有祖先结点，需更新平衡因子
				}
				else //待删除结点的左右子树均不为空
				{
					//替换法删除
					//寻找待删除结点右子树当中key值最小的结点作为实际删除结点
					Node* minParent = cur;
					Node* minRight = cur->_right;
					while (minRight->_left)
					{
						minParent = minRight;
						minRight = minRight->_left;
					}
					cur->_kv.first = minRight->_kv.first; //将待删除结点的key改为minRight的key
					cur->_kv.second = minRight->_kv.second; //将待删除结点的value改为minRight的value
					delParentPos = minParent; //标记实际删除结点的父结点
					delPos = minRight; //标记实际删除的结点
					break; //删除结点有祖先结点，需更新平衡因子
				}
			}
		}
		if (delParentPos == nullptr) //delParentPos没有被修改过，说明没有找到待删除结点
		{
			return false;
		}

		//记录待删除结点及其父结点（用于后续实际删除）
		Node* del = delPos;
		Node* delP = delParentPos;

		//更新平衡因子
		while (delPos != _root) //最坏一路更新到根结点
		{
			if (delPos == delParentPos->_left) //delParentPos的左子树高度降低
			{
				delParentPos->_bf++; //delParentPos的平衡因子++
			}
			else if (delPos == delParentPos->_right) //delParentPos的右子树高度降低
			{
				delParentPos->_bf--; //delParentPos的平衡因子--
			}
			//判断是否更新结束或需要进行旋转
			if (delParentPos->_bf == 0)//需要继续往上更新平衡因子
			{
				//delParentPos树的高度变化，会影响其父结点的平衡因子，需要继续往上更新平衡因子
				delPos = delParentPos;
				delParentPos = delParentPos->_parent;
			}
			else if (delParentPos->_bf == -1 || delParentPos->_bf == 1) //更新结束
			{
				break; //delParent树的高度没有发生变化，不会影响其父结点及以上结点的平衡因子
			}
			else if (delParentPos->_bf == -2 || delParentPos->_bf == 2) //需要进行旋转（此时delParentPos树已经不平衡了）
			{
				if (delParentPos->_bf == -2)
				{
					if (delParentPos->_left->_bf == -1)
					{
						Node* tmp = delParentPos->_left; //记录delParentPos右旋转后新的根结点
						RotateR(delParentPos); //右单旋
						delParentPos = tmp; //更新根结点
					}
					else if (delParentPos->_left->_bf == 1)
					{
						Node* tmp = delParentPos->_left->_right; //记录delParentPos左右旋转后新的根结点
						RotateLR(delParentPos); //左右双旋
						delParentPos = tmp; //更新根结点
					}
					else //delParentPos->_left->_bf == 0
					{
						Node* tmp = delParentPos->_left; //记录delParentPos右旋转后新的根结点
						RotateR(delParentPos); //右单旋
						delParentPos = tmp; //更新根结点
						//平衡因子调整
						delParentPos->_bf = 1;
						delParentPos->_right->_bf = -1;
						break; //更正
					}
				}
				else //delParentPos->_bf == 2
				{
					if (delParentPos->_right->_bf == -1)
					{
						Node* tmp = delParentPos->_right->_left; //记录delParentPos右左旋转后新的根结点
						RotateRL(delParentPos); //右左双旋
						delParentPos = tmp; //更新根结点
					}
					else if (delParentPos->_right->_bf == 1)
					{
						Node* tmp = delParentPos->_right; //记录delParentPos左旋转后新的根结点
						RotateL(delParentPos); //左单旋
						delParentPos = tmp; //更新根结点
					}
					else //delParentPos->_right->_bf == 0
					{
						Node* tmp = delParentPos->_right; //记录delParentPos左旋转后新的根结点
						RotateL(delParentPos); //左单旋
						delParentPos = tmp; //更新根结点
						//平衡因子调整
						delParentPos->_bf = -1;
						delParentPos->_left->_bf = 1;
						break; //更正
					}
				}
				//delParentPos树的高度变化，会影响其父结点的平衡因子，需要继续往上更新平衡因子
				delPos = delParentPos;
				delParentPos = delParentPos->_parent;
				//break; //error
			}
			else
			{
				assert(false); //在删除前树的平衡因子就有问题
			}
		}
		//进行实际删除
		if (del->_left == nullptr) //实际删除结点的左子树为空
		{
			if (del == delP->_left) //实际删除结点是其父结点的左孩子
			{
				delP->_left = del->_right;
				if (del->_right)
					del->_right->_parent = parent;
			}
			else //实际删除结点是其父结点的右孩子
			{
				delP->_right = del->_right;
				if (del->_right)
					del->_right->_parent = parent;
			}
		}
		else //实际删除结点的右子树为空
		{
			if (del == delP->_left) //实际删除结点是其父结点的左孩子
			{
				delP->_left = del->_left;
				if (del->_left)
					del->_left->_parent = parent;
			}
			else //实际删除结点是其父结点的右孩子
			{
				delP->_right = del->_left;
				if (del->_left)
					del->_left->_parent = parent;
			}
		}
		delete del; //实际删除结点
		return true;
	}

7. AVL树的遍历

中序遍历和二叉树的中序实现一样，只不过因为中序是递归遍历，涉及到传参，所以需要写一个子函数。

代码示例

private:
	// 中序遍历（子函数）
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}
public:
	// 中序遍历
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

8. AVL树的查找

AVL树的查找与二叉搜索树一样：

• 若树为空树，则查找失败，返回 nullptr。
• 若树不为空树，则有以下三种情况：
  • 若 key 值小于当前结点的值，则应该在该结点的左子树当中进行查找。
  • 若 key 值大于当前结点的值，则应该在该结点的右子树当中进行查找。
  • 若 key 值等于当前结点的值，则查找成功，返回对应结点。

代码示例

public:
	// 查找函数
	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key) // key值大于该结点的值
			{
				cur = cur->_left; // 在该结点的右子树当中查找
			}
			else if (cur->_kv.first < key) // key值小于该结点的值
			{
				cur = cur->_right; // 在该结点的左子树当中查找
			}
			else // 当前节点的值等于key值
			{
				return cur; //返回该结点
			}
		}
		return nullptr; //查找失败
	}

9. AVL树的高度

这里和求二叉树的深度是一样的方式，采用分治的思想：

• 若为空树，则深度为 0。

• 若不为空树，则深度 = 左右子树中深度最大的值 + 1（为什么要加1呢？因为还有第一层，也就是根节点这一层！）

代码示例

private:
	// 求树的高度（子函数）
	int _Height(Node* root)
	{
		if (root == nullptr) // 空树高度为0
			return 0;

		int lh = _Height(root->_left); // 递归计算左子树高度
		int rh = _Height(root->_right); // 递归计算右子树高度

		return lh > rh ? lh + 1 : rh + 1; // 左树高度或者右树高度大的哪一个，然后再+1，就是整棵树的高度
	}
public:
	// 树的高度
	int Height()
	{
		return _Height(_root);
	}

10. AVL树的验证

AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分为下面两步：

（1）验证其为二叉搜索树

• 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树

（2）验证其为平衡树

• 每个节点子树高度差的绝对值不超过 1（注意节点中如果没有平衡因子）

• 节点的平衡因子是否计算正确

检测二叉树是否平衡的代码

private:
	// 判断是否为平衡二叉树（子函数）
	bool _IsBalanceTree(Node* root)
	{
		// 空树也是AVL树
		if (nullptr == root)
			return true;

		// 计算pRoot节点的平衡因子：即pRoot左右子树的高度差
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = rightHeight - leftHeight;

		// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
		// pRoot平衡因子的绝对值超过1，则一定不是AVL树
		if (abs(diff) >= 2)
		{
			cout << root->_kv.first << "节点平衡因子异常" << endl;
			return false;
		}

		if (diff != root->_bf)
		{
			cout << root->_kv.first << "节点平衡因子不符合实际" << endl;
			return false;
		}

		// pRoot的左和右如果都是AVL树，则该树一定是AVL树
		return _IsBalanceTree(root->_left)
			&& _IsBalanceTree(root->_right);
	}
public:
	// 判断是否为平衡二叉树
	bool IsBalanceTree()
	{
		return _IsBalanceTree(_root);
	}

🍑 数据测试

（1）测试一组有序值

// 插入有序值
void TestAVLTree1()
{
	const int N = 20;

	vector<int> v;
	v.reserve(N);
	srand(time(0));
	for (size_t i = 0; i < N; ++i)
	{
		v.push_back(i);
	}

	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
	}

	if (t.IsBalanceTree())
	{
		cout << "AVL树平衡" << endl;
	}
	else
	{
		cout << "AVL树不平衡" << endl;
	}
	
	cout << "AVL树高度：" << t.Height() << endl;

	cout << "中序遍历：";
	t.InOrder();
}

运行结果

（2）测试一组随机值

// 插入随机值
void TestAVLTree2()
{
	const size_t N = 20;

	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; ++i)
	{
		v.push_back(rand());
	}

	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
	}
	if (t.IsBalanceTree())
	{
		cout << "AVL树平衡" << endl;
	}
	else
	{
		cout << "AVL树不平衡" << endl;
	}
	cout << "AVL树高度：" << t.Height() << endl;

	cout << "中序遍历：";
	t.InOrder();
}

运行结果

11. AVL树优缺点分析

优点：

• 平衡二叉树的优点不言而喻，相对于二叉排序树（BST）而言，平衡二叉树避免了二叉排序树可能出现的最极端情况（斜树）问题，其平均查找的时间复杂度为 $O(logN)$

缺点：

• 平衡二叉树为了保持平衡，动态进行插入和删除操作的代价也会增加。因此出现了后来的红黑树（下篇文章会讲解）

时间复杂度分析：

• 左旋和右旋操作仅需要改变几个指针，时间复杂度为 $O(1)$，更新结点的深度以及获得平衡因子仅需要常数时间，所以平衡二叉树的删除操作的时间复杂度与二叉排序树BST的删除操作一样，均为 $O(h)$，其中 h 为树的高度。由于AVL 树是平衡的，所以高度 $h=logN$ ，因此，AVL 删除操作的时间复杂度为 $O(logN)$

总结：文章来源地址https://www.toymoban.com/news/detail-784525.html

• AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过 1，这样可以保证查询时高效的时间复杂度，即$O(logN)$。
• 但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。
• 因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的（即不会改变），可以考虑AVL树，但一个结构经常修改，就不太适合。

到了这里，关于C/C++数据结构（十一）—— 平衡二叉树（AVL树）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！