深度优先搜索算法(Depth First Search,简称DFS):一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
一、基本思想
- 为了求得问题的解,先选择某一种可能情况向前探索;
- 在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索;
- 如此反复进行,直至得到解或证明无解。
二、操作步骤:
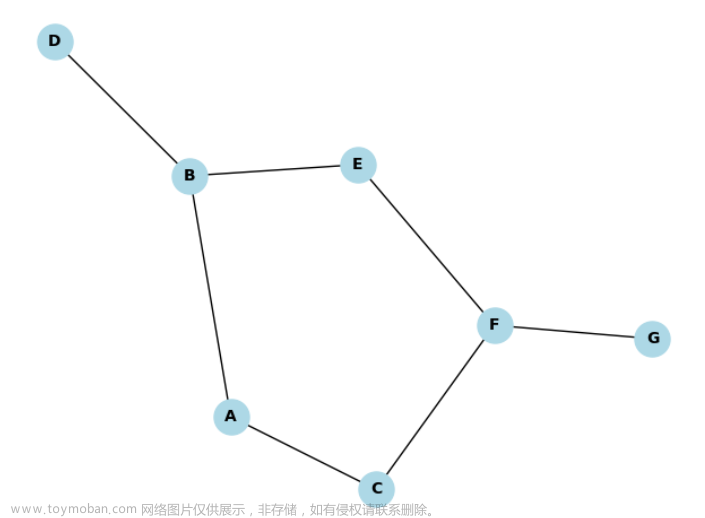
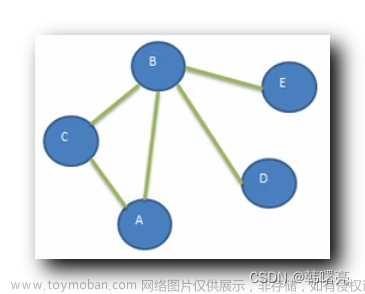
- 初始原点为v0,使用深度优先搜索,首先访问 v0 -> v1 -> v2 -> v5,到 v5 后面没有结点,则回溯到 v1 ,即最近的且连接有没访问结点的结点v1;
- 此次从 v1 出发,访问 v1 -> v4 -> v6 -> v3,此时与v3相连的两个结点 v0 与 v6 都已经访问过,回溯到 v6 (v6 具有没访问过的结点);
- 此次从 v6 出发,访问 v6 -> v7,到 v7 后面没有结点,回溯;
- 一直回溯到源点 v0 ,没有没访问过的结点,程序结束。
注:下面图中箭头为回溯方向
三、模板
C模板:
int a[510]; //存储每次选出来的数据
int book[510]; //标记是否被访问
int ans = 0; //记录符合条件的次数
void DFS(int cur){
if(cur == k){ //k个数已经选完,可以进行输出等相关操作
for(int i = 0; i < cur; i++){
printf("%d ", a[i]);
}
ans++;
return ;
}
for(int i = 0; i < n; i++){ //遍历 n个数,并从中选择k个数
if(!book[i]){ //若没有被访问
book[i] = 1; //标记已被访问
a[cur] = i; //选定本数,并加入数组
DFS(cur + 1); //递归,cur+1
book[i] = 0; //释放,标记为没被访问,方便下次引用
}
}
}
C++模板:
vector<int> a; // 记录每次排列
vector<int> book; //标记是否被访问
void DFS(int cur, int k, vector<int>& nums){
if(cur == k){ //k个数已经选完,可以进行输出等相关操作
for(int i = 0; i < cur; i++){
printf("%d ", a[i]);
}
return ;
}
for(int i = 0; i < k; i++){ //遍历 n个数,并从中选择k个数
if(book[nums[i]] == 0){ //若没有被访问
a.push_back(nums[i]); //选定本输,并加入数组
book[nums[i]] = 1; //标记已被访问
DFS(cur + 1, n, nums); //递归,cur+1
book[nums[i]] = 0; //释放,标记为没被访问,方便下次引用
a.pop_back(); //弹出刚刚标记为未访问的数
}
}
}
四、例题
学算法当然要刷题领悟啦,不然就是我这种一看就会(只是背了下来),一写就废的菜鸡 ^ - ^
下面就让我们一起看看这个俗称不撞南墙不回头算法都有哪些例题!!!
1、排列问题
题目一:
设有n个整数的集合{1,2,…,n},从中取出任意r个数进行排列(1<=r<n<=10),试列出所有的排列。
示例:
输入:n = 4, r = 3
输出:
1 2 3
1 2 4
1 3 2
1 3 4
1 4 2
1 4 3
2 1 3
2 1 4
2 3 1
2 3 4
2 4 1
2 4 3
3 1 2
3 1 4
3 2 1
3 2 4
3 4 1
3 4 2
4 1 2
4 1 3
4 2 1
4 2 3
4 3 1
4 3 2
24
分析:
在这里某个元素按不同次序出现的组合应视为不同的排列。例如:1 2 3和2 1 3,元素均为1.2.3,只是排列顺序不同,因此应视为元素1.2.3的不同排列。
实现过程:
- 定义两个数组 a[] 与 book[] ,其中数组a保存每次的排列数据,数组book用来标记 i 这个数是否被访问;
- 初始化相关数据;
- 递归填数并判断第i个数填入是否合法:
合法:填数,并判断是否已经到达环的终点。如果到达终点,打印结果;否则,继续填下一个数;
不合法:选择下一种可能。
特别地,当n=r时,称为n的全排列。实现时只需把下面程序的终点改为cur==n即可。
AC代码:
#include<iostream>
using namespace std;
int n, r, ans; //r个数进行全排列 ans为排列个数
int book[510]; //标记是否被访问
int a[510]; //记录每次的排列数据
void DFS(int cur){ //从{1,2,...,n}中取r个数构成的排列
if(cur == r){ //已经去够r个数
for(int i = 0; i < cur; i++){ //循环输出
cout << a[i] << ' ';
}
cout << endl;
ans++; //数量加1
return ;
}
for(int i = 1; i <= n; i++){ //循环遍历保证不漏
if(!book[i]){ //若没访问过
book[i] = 1; //标记已访问
a[cur] = i; //i符合条件加入
DFS(cur + 1); //寻找一个数字
book[i] = 0; //回溯:清除标记
}
}
}
int main(){
cin >> n >> r;
DFS(0);
cout << ans << endl;
return 0;
}
题目二:
【LeetCode每日一题】46. 全排列 —— DFS算法(C/C++)
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
分析:
具体分析与提交答案请点击题目,这里就不在一一赘述!!!
AC代码:
vector<vector<int>> ans; //记录答案
vector<int> a; // 记录每次排列
map<int, int> book; //标记是否被访问
void DFS(int cur, int n, vector<int>& nums){
if(cur == n){
ans.push_back(a);
return ;
}
for(int i = 0; i < n; i++){
if(book[nums[i]] == 0){
a.push_back(nums[i]);
book[nums[i]] = 1;
DFS(cur + 1, n, nums);
book[nums[i]] = 0;
a.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
int n = nums.size();
DFS(0, n, nums);
return ans;
}
题目三:
【LeetCode每日一题】784. 字母大小写全排列 —— DFS算法(C/C++)
给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。
返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。
示例 1:
输入:s = “a1b2”
输出:[“a1b2”, “a1B2”, “A1b2”, “A1B2”]
示例 2:
输入: s = “3z4”
输出: [“3z4”,“3Z4”]
提示:
1 <= s.length <= 12
s 由小写英文字母、大写英文字母和数字组成
分析:
具体思路方案与题目一差不多,这里我说一些需要用到的别的东西 ^ -^
在本题中首先使用 isdigit() 函数判断,若为数字则直接进行递归,即不用管;若为字母则使用 tolower() 函数——变为小写,然后递归,再使用 toupper() 函数——变为大写,递归。
若不明白 isdigit() 函数请看这篇:isdigit函数详解
AC代码:
vector<string> ans; //记录最终结果
void DFS(int cur, string s){
if(cur == s.size()){
ans.push_back(s);
return ;
}
if(isdigit(s[cur])){
DFS(cur + 1, s);
}else{
s[cur] = tolower(s[cur]);
DFS(cur + 1, s);
s[cur] = toupper(s[cur]);
DFS(cur + 1, s);
}
}
vector<string> letterCasePermutation(string s) {
DFS(0, s);
return ans;
}
2、组合问题
题目一:
【LeetCode每日一题】77. 组合 —— DFS算法(C/C++)
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 :
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
提示:
1 <= n <= 20
1 <= k <= n
分析:
具体思路与排序差不多,具体需要注意的是,这里某种数字组合的多种排列视为相同情况,因此需 “去重” 。
一种可行的方案是填数的时候:
- 如果当前填的是第一个数,则直接填入;
- 在 1 的基础上,后面填入的数都要比前面的数大,因此要进行大小的比较。如果不符合条件,则不能填入。这样既能保证每种组合中数是递增的,也能保证组合是按字典序输出的。
AC代码:
vector<vector<int>> a; //存储排列数据
vector<int> b; // 存储每次的排列数据
void DFS(int cur, int n, int k){
if(cur == k){
a.push_back(b);
return ;
}
for(int i = 1; i <= n; i++){
int temp;
if(cur > 0) temp = b.back(); //返回b数组的最后一个元素
if((cur == 0) || (cur > 0 && i > temp)){ //第一个数或者后面的数大于前面的数
b.push_back(i); //符合加入
DFS(cur + 1, n, k); //递归选择下一个数
b.pop_back(); //弹出
}
}
}
vector<vector<int>> combine(int n, int k) {
DFS(0, n, k);
return a;
}
3、n皇后问题
题目一:
洛谷——P1219 [USACO1.5]八皇后 Checker Challenge
一个如下的 6 * 6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 33 个解。最后一行是解的总个数。
输入格式:
一行一个正整数 n,表示棋盘是 n×n 大小的。
输出格式:
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
示例:
输入:6
输出:
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
分析:
问题的关键在于如何判定某个皇后所在的行、列、斜线上是否有别的皇后;可以从矩阵的特点上找到规律,如果在同一行,则行号相同;如果在同一列上,则列号相同;如果同在/斜线上的行列值之和相同;如果同在\斜线上的行列值之差相同;从下图可验证:
在摆放皇后时,可以”按行摆放”(这样就保证了皇后不会横向攻击)。即:
(1)起点为 dfs(0),即从第0行开始摆放皇后,逐行进行。同时使用一维数组 map 保存第 cur 行的皇后摆放的列,也就是说每次尝试摆放皇后的位置坐标为 (cur, map[cur]);
(2)逐列遍历,若发现位置 (i, map[j]) 与位置 (cur, map[cur]) 在同一列 或 同一主对角线 或 同一副对角线上时,摆放失败,该方案”作废”,继续执行;
(3)若摆放成功,则 dfs(cur+1),表示继续摆放下一行,过程同上;
(4)当 cur=n,即n行皇后均摆放完成时,表示该方案可行,总方案数+1。
AC代码:
#include<iostream>
using namespace std;
const int M = 20;
int ans = 0, n;
int a[M]; //标记i行 纵坐标为a[i]
void dfs(int cur){
int flag = 1; //标记该序列是否可行
if(cur == n){
if(ans < 3){
for(int i = 0; i < n-1; i++){
cout << a[i] << " ";
}
cout << a[n-1] << endl;
}
ans++;
return;
}
for(int i = 1; i <= n; i++){
flag = 1;
a[cur] = i;
for(int j = 0; j < cur; j++){
if(a[cur] == a[j] || cur+a[cur] == j+a[j] || cur-a[cur] == j-a[j]){
flag = 0;
break;
}
}
if(flag == 1){
dfs(cur+1);
}
}
}
int main(){
cin >> n;
dfs(0);
cout << ans << endl;
return 0;
}
4、素数问题
素数问题有好多经典题型,例如素数环、素数和、和为素数等等;下面就来介绍几个经典例题,大家一起来学习吧。
题目一:
洛谷——P1036 [NOIP2002 普及组] 选数
已知 n 个整数 x1,x2,……,xn,以及 1 个整数 k(k<nk<n)。从 n 个整数中任选 k 个整数相加,可分别得到一系列的和。例如当 n=4,k=3,4 个整数分别为 3,7,12,19 时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=29。
输入格式:
第一行两个空格隔开的整数 n,k(1≤n≤20,k<n)。
第二行 n 个整数,分别为 x1,x2,……,xn(1 ≤ xi ≤ 5*10^6)
输出格式:
输出一个整数,表示种类数。
示例:
输入:
4 3
3 7 12 19
输出:
1文章来源:https://www.toymoban.com/news/detail-784579.html
分析:
本题是 dfs 中的一个非常经典的问题——素数问题中的一个分支,总体思路同上,都是循环遍历加判断 cur == k ;与上面不同的地方在于本类问题需要判断素数,下面我介绍一个判断素数的方法:文章来源地址https://www.toymoban.com/news/detail-784579.html
- 0,1 直接返回 false;
- 循环从 2 开始,根号下 x 结束,若 x % i 为 0 ,说明 x 有除 1 和它本身的其他因数,返回 false ;
AC代码:
#include<iostream>
using namespace std;
int a[30], book[30];
int n, k, cnt = 0;
bool Judge(int x){
for(int i = 2; i*i <= x; i++){
if(x % i == 0) return false;
}
return true;
}
void dfs(int cur, int sum, int t){
if(cur == k){
if(Judge(sum)) cnt++;
return;
}
for(int i = t; i < n; i++){
dfs(cur+1, sum+a[i], i+1);
}
return;
}
int main(){
fill(book, book + 30, 0);
cin >> n >> k;
for(int i = 0; i < n; i++){
cin >> a[i];
}
dfs(0, 0, 0);
cout << cnt << endl;
return 0;
}
到了这里,关于DFS (深度优先搜索) 算法详解 + 模板 + 例题,这一篇就够了的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!