原文链接:https://arxiv.org/abs/2312.09243
1. 引言
3D目标检测任务受到无限类别和长尾问题的影响。3D占用预测则不同,其关注场景的几何重建,但多数方法需要从激光雷达点云获取的3D监督信号。
本文提出OccNeRF,一种自监督多相机占用预测模型。首先使用图像主干提取2D特征。为节省空间,本文直接插值2D特征得到3D体素特征,而不使用交叉注意力。此外,本文考虑相机视野的无限空间,因此将占用场参数化,以表达无界环境。本文将整个3D空间分为内部和外部区域,其中内部区域保留原始坐标,外部区域使用收缩坐标。还设计专门的采样策略和神经渲染,将参数化占用场转化为多相机深度图。
使用渲染图像和训练图像之间的损失来监督占用预测效果不佳,因此本文使用时间光度损失作为监督,其常用于自监督深度估计任务。还使用了多帧光度约束,以更好地利用时间线索。对于语义占用,本文提出3个策略将类别名映射为提示,并输入预训练的开放词汇分割模型获取2D语义标签。然后使用额外的语义头渲染语义图像并受上述标签监督。
3. 方法
3.1 概述

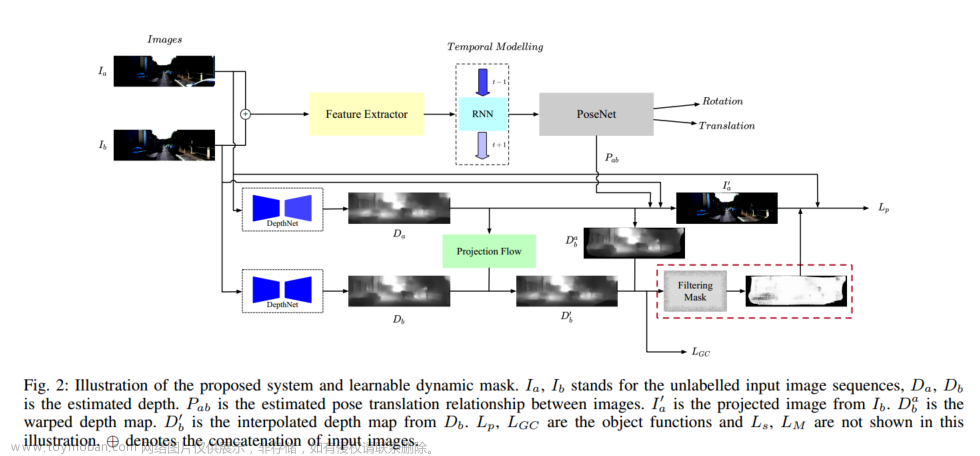
如上图所示为本文方法的流程。多视图图像输入
{
I
i
}
i
=
1
N
\{I^i\}_{i=1}^N
{Ii}i=1N首先通过2D主干提取特征
{
X
i
}
i
=
1
N
\{X^i\}_{i=1}^N
{Xi}i=1N,并根据相机内参
{
K
i
}
i
=
1
N
\{K^i\}_{i=1}^N
{Ki}i=1N和外参
{
T
i
}
i
=
1
N
\{T^i\}_{i=1}^N
{Ti}i=1N插值到3D空间。然后使用坐标参数化将无限的距离压缩为有限占用场。使用体积渲染将占用转化为多视图深度图,并通过光度损失监督。最后,使用预训练的开放词汇分割模型获取2D语义标签。
3.2 参数化占用场
需要在内部区域(自车附近的区域,感兴趣区)保留高分辨率,而外部区域也是必要的,但影响较小,需要压缩空间表达以节省空间。使用可调整感兴趣区和压缩阈值的体素坐标参数化函数:
f
(
r
)
=
{
α
⋅
r
′
∣
r
′
∣
≤
1
r
′
∣
r
′
∣
⋅
(
1
−
(
1
−
α
)
2
α
∣
r
′
∣
−
2
α
+
1
)
∣
r
′
∣
>
1
f(r)=\left\{\begin{matrix}\alpha\cdot r'&|r'|\leq1\\\frac{r'}{|r'|}\cdot(1-\frac{(1-\alpha)^2}{\alpha|r'|-2\alpha+1})&|r'|>1\end{matrix}\right.
f(r)={α⋅r′∣r′∣r′⋅(1−α∣r′∣−2α+1(1−α)2)∣r′∣≤1∣r′∣>1
其中
r
′
=
r
/
r
b
r'=r/r_b
r′=r/rb为
r
∈
{
x
,
y
,
z
}
r\in\{x,y,z\}
r∈{x,y,z}的归一化坐标,
f
(
r
)
∈
(
−
1
,
1
)
f(r)\in(-1,1)
f(r)∈(−1,1)为归一化参数化坐标。
r
b
r_b
rb为内部区域的界(各坐标维度对应不同的值),
α
∈
[
0
,
1
]
\alpha\in[0,1]
α∈[0,1]为感兴趣区在参数化空间中的比例,越高表示使用越多的空间表达内部区域。上述公式的两个分支在
r
=
r
b
r=r_b
r=rb处有相同的值和梯度。
为从2D视图得到3D体素特征,首先在参数化空间生成体素对应的点
P
p
c
=
[
x
p
c
,
y
p
c
,
z
p
c
]
T
\mathcal{P}_{pc}=[x_{pc},y_{pc},z_{pc}]^T
Ppc=[xpc,ypc,zpc]T,然后映射回自车坐标系:
P
=
[
f
x
−
1
(
x
p
c
)
,
f
y
−
1
(
y
p
c
)
,
f
z
−
1
(
z
p
c
)
]
T
\mathcal{P}=[f^{-1}_x(x_{pc}),f^{-1}_y(y_{pc}),f^{-1}_z(z_{pc})]^T
P=[fx−1(xpc),fy−1(ypc),fz−1(zpc)]T
然后投影到2D图像平面(
proj
(
)
\text{proj}()
proj())并使用双线性插值(
⟨
⋅
⟩
\langle\cdot\rangle
⟨⋅⟩)得到特征:
F
i
=
X
i
⟨
proj
(
P
,
T
i
,
K
i
)
⟩
\mathcal{F}^i=X^i\langle\text{proj}(\mathcal{P},T^i,K^i)\rangle
Fi=Xi⟨proj(P,Ti,Ki)⟩
将来自多个视图的特征取平均,得到体素特征。最后,使用3D卷积提取3D特征并预测占用。
3.3 多帧深度估计
为将占用场投影为多视图深度图,使用NeRF的体积渲染。对于待进行深度渲染的像素,从相机中心
o
o
o投射指向像素的射线(方向
d
d
d),得到
v
(
t
)
=
o
+
t
d
v(t)=o+td
v(t)=o+td。然后沿射线采样
L
L
L个点
{
t
k
}
k
=
1
L
\{t_k\}_{k=1}^L
{tk}k=1L以得到密度
σ
(
t
k
)
\sigma(t_k)
σ(tk)。按下式计算像素的深度:
D
(
v
)
=
∑
k
=
1
L
T
(
t
k
)
(
1
−
exp
(
−
σ
(
t
k
)
δ
k
)
)
t
k
D(v)=\sum_{k=1}^L T(t_k)(1-\exp(-\sigma(t_k)\delta_k))t_k
D(v)=k=1∑LT(tk)(1−exp(−σ(tk)δk))tk其中
T
(
t
k
)
=
exp
(
−
∑
k
′
=
1
k
−
1
σ
(
t
k
′
)
δ
k
′
)
T(t_k)=\exp(-\sum_{k'=1}^{k-1}\sigma(t_{k'})\delta_{k'})
T(tk)=exp(−∑k′=1k−1σ(tk′)δk′),
δ
k
=
t
k
+
1
−
t
k
\delta_k=t_{k+1}-t_k
δk=tk+1−tk为样本点的间距。
由于
o
o
o在坐标系原点附近,本文直接从
U
[
0
,
1
]
U[0,1]
U[0,1]采样参数化坐标系下的
L
(
r
)
L(r)
L(r)个点,然后根据
f
−
1
f^{-1}
f−1计算自车坐标系下的
{
t
k
}
k
=
1
L
(
r
)
\{t_k\}_{k=1}^{L(r)}
{tk}k=1L(r)。
L
(
v
)
L(v)
L(v)与
r
b
(
v
)
r_b(v)
rb(v)按下式计算:
r
b
(
v
)
=
(
d
⋅
i
l
x
)
2
+
(
d
⋅
j
l
y
)
2
+
(
d
⋅
k
l
z
)
2
2
∥
d
∥
L
(
v
)
=
2
r
b
(
v
)
α
d
v
r_b(v)=\frac{\sqrt{(d\cdot il_x)^2+(d\cdot jl_y)^2+(d\cdot kl_z)^2}}{2\|d\|}\\ L(v)=\frac{2r_b(v)}{\alpha d_v}
rb(v)=2∥d∥(d⋅ilx)2+(d⋅jly)2+(d⋅klz)2L(v)=αdv2rb(v)其中
i
,
j
,
k
i,j,k
i,j,k为
x
,
y
,
z
x,y,z
x,y,z轴的单位向量,
l
x
,
l
y
,
l
z
l_x,l_y,l_z
lx,ly,lz为内部区域的长宽高,
d
v
d_v
dv为体素大小。本文直接预测渲染权重而非密度。
传统的监督方法计算渲染RGB与原始RGB图像的损失,但实验表明这样的性能不佳。这可能是视图数量太少且场景太大。本文使用时间光度损失,将相邻帧根据渲染深度和相对姿态投影到当前帧,计算投影图像与原始图像的重建损失:
L
p
c
i
=
β
2
(
1
−
SSIM
(
I
i
,
I
^
i
)
)
+
(
1
−
β
)
∥
I
i
,
I
^
i
∥
1
\mathcal{L}_{pc}^i=\frac{\beta}{2}(1-\text{SSIM}(I^i,\hat{I}^i))+(1-\beta)\|I^i,\hat{I}^i\|_1
Lpci=2β(1−SSIM(Ii,I^i))+(1−β)∥Ii,I^i∥1其中
I
^
i
\hat{I}^i
I^i为投影图像,
β
=
0.85
\beta=0.85
β=0.85。此外,还使用逐像素最小重投影损失和自动掩膜静态像素。对每个视图渲染短序列以进行多帧光度损失。
3.4 开放词汇语义监督
多视图图像的2D图像语义标签提供像素级监督,使网络能捕捉几何一致性和体素空间关系。本文使用预训练的开放词汇模型GroundedSAM,生成2D语义标签。该模型能在给定类别名称时得到语义匹配的2D标签。
当处理
c
c
c类物体时,使用3种方法决定Grounding DINO(以文字提示进行目标检测的开放世界模型)的输入提示:同义替换(如使用“汽车”的同义词“小轿车”以与“卡车”和“公交车”区分)、细分类别(如“人造物”被分为“建筑”、“广告牌”、“桥”等以加强区分)、引入额外信息(如引入“自行车手”以促进自行车上人的检测)。得到检测边界框与分数(logits,置信度分数在sigmoid归一化前的值)、短语后,输入SAM(分割一切模型)生成
M
M
M个精确的分割二值掩膜,并与Grounding DINO输出的分数相乘。这样,每个像素的分数为
{
l
i
}
i
=
1
M
\{l_i\}_{i=1}^M
{li}i=1M。使用下式得到逐像素类别:
S
p
i
x
=
ψ
(
arg max
i
l
i
)
\mathcal{S}^{pix}=\psi(\argmax_il_i)
Spix=ψ(iargmaxli)其中
ψ
\psi
ψ将
l
i
l_i
li的索引根据短语映射为类别标签的函数。若某像素不属于任何类别(得到
M
M
M个0分),则标记为“不确定”标签。
使用
c
c
c个通道输出的语义头将体素特征映射到语义输出,记为
S
(
x
)
S(x)
S(x),并使用类似3.3节的体积渲染公式得到逐像素语义渲染输出:
S
^
p
i
x
(
r
)
=
∑
k
=
1
L
s
T
(
t
k
)
(
1
−
exp
(
−
σ
(
t
k
)
δ
k
)
)
S
(
t
k
)
\hat{\mathcal{S}}^{pix}(r)=\sum_{k=1}^{L_s}T(t_k)(1-\exp(-\sigma(t_k)\delta_k))S(t_k)
S^pix(r)=k=1∑LsT(tk)(1−exp(−σ(tk)δk))S(tk)
为节省空间,本文不渲染“不确定”标签的像素,且只渲染中心帧,并将采样点数降为
L
s
=
L
/
4
L_s=L/4
Ls=L/4。总损失如下:
L
t
o
t
a
l
=
∑
i
L
p
e
i
+
λ
L
s
e
m
i
(
S
^
p
i
x
,
S
p
i
x
)
\mathcal{L}_{total}=\sum_i\mathcal{L}_{pe}^i+\lambda\mathcal{L}_{sem}^i(\hat{\mathcal{S}}^{pix},\mathcal{S}^{pix})
Ltotal=i∑Lpei+λLsemi(S^pix,Spix)其中
L
s
e
m
\mathcal{L}_{sem}
Lsem为交叉熵损失。
4. 实验
4.1 实验设置
数据集:自监督深度估计任务真值通过激光雷达点云投影到图像上获得,以进行评估。语义占用使用Occ3D-nuScenes基准。
实施细节:图像主干使用ResNet-101。深度渲染时渲染5帧(关键帧和其相邻的4帧非关键帧)中的3帧。
评估指标:深度估计使用Abs Rel、Sq Rel、RMSE、RMSE log与
δ
<
t
\delta<t
δ<t指标。语义占用预测使用各类mIoU(仅对图像可见体素进行评估)。
4.2 自监督深度估计
本任务不使用预训练模型。实验表明,本文方法能大幅超过其余SotA。
需要注意的是,部分方法可能仅使用关键帧图像作为训练输入,而本文的方法使用了非关键帧图像。
4.3 语义占用预测
实验表明,本文方法能超过其余自监督方法,且能达到一些全监督方法相当的性能。对于某些类别,本文的方法能超过所有监督方法,但对小型物体,本文方法与监督方法之间的差距还很大。这可能是目前的开放词汇模型会忽略小物体。
4.4 消融研究
监督方法:使用渲染RGB色彩与真值的损失作为监督,性能很差。这可能是因为仅有少量的视角图像,NeRF难以学习场景结构。而使用时间光度损失可以利用相邻帧的几何线索。
坐标参数化:使用收缩坐标能提高性能;在此基础上使用本文提出的采样策略替代均匀采样策略能进一步提高性能。
语义标签生成:直接使用SAM的输出分数,性能较差,因其有噪声且不连续;使用原始类别名称作为开放词汇模型输入生成2D监督。结果同样较差,因其不提供细粒度语义指导,会带来模糊性。
5. 局限性与未来工作
本文的方法在推断时仅使用单帧输入进行占用预测,因此不能预测占用流。此外,本文方法的性能受到开放词汇分割模型性能的限制。
附录
A. 参数化占用场推导

上图所示为原始无界空间与参数化有界空间的比较。内部空间需要线性映射以保留高分辨率;而外部空间点的分布于视差成比例,而视差与距离成反比。可得变换函数:
f
(
r
)
=
{
α
⋅
r
′
∣
r
′
∣
≤
1
r
′
∣
r
′
∣
⋅
(
1
−
a
∣
r
′
∣
+
b
)
∣
r
′
∣
>
1
f(r)=\left\{\begin{matrix}\alpha\cdot r'&|r'|\leq1\\\frac{r'}{|r'|}\cdot(1-\frac{a}{|r'|+b})&|r'|>1\end{matrix}\right.
f(r)={α⋅r′∣r′∣r′⋅(1−∣r′∣+ba)∣r′∣≤1∣r′∣>1
保证上述两段在
r
′
=
1
r'=1
r′=1处连续且导数连续,可解得
a
,
b
a,b
a,b的值。文章来源:https://www.toymoban.com/news/detail-784588.html
C. 评估指标
- Abs Rel: 1 ∣ T ∣ ∑ d ∈ T ∣ d − d ∗ ∣ / d ∗ \frac{1}{|T|}\sum_{d\in T}|d-d^*|/d^* ∣T∣1∑d∈T∣d−d∗∣/d∗
- Sq Rel: 1 ∣ T ∣ ∑ d ∈ T ∣ d − d ∗ ∣ 2 / d ∗ \frac{1}{|T|}\sum_{d\in T}|d-d^*|^2/d^* ∣T∣1∑d∈T∣d−d∗∣2/d∗
- RMSE: 1 ∣ T ∣ ∑ d ∈ T ∣ d − d ∗ ∣ 2 \sqrt{\frac{1}{|T|}\sum_{d\in T}|d-d^*|^2} ∣T∣1∑d∈T∣d−d∗∣2
- RMSE log: 1 ∣ T ∣ ∑ d ∈ T ∣ log d − log d ∗ ∣ 2 \sqrt{\frac{1}{|T|}\sum_{d\in T}|\log d-\log d^*|^2} ∣T∣1∑d∈T∣logd−logd∗∣2
- δ < t \delta<t δ<t:满足 max ( d d ∗ , d ∗ d ) = δ < t \max(\frac{d}{d^*},\frac{d^*}{d})=\delta<t max(d∗d,dd∗)=δ<t的像素所占的百分比。
其中 T T T为像素集合。文章来源地址https://www.toymoban.com/news/detail-784588.html
到了这里,关于【论文阅读】OccNeRF: Self-Supervised Multi-Camera Occupancy Prediction with Neural Radiance Fields的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!