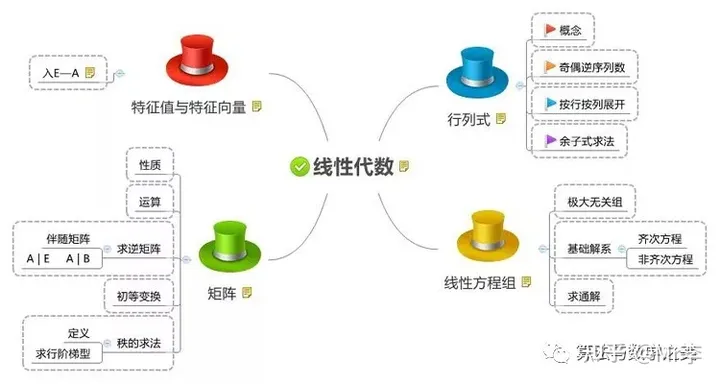
线性代数是数学的一个分支,主要研究向量空间、线性变换、矩阵等概念及其应用。以下是线性代数的应用场景、学习路线及要点分析:
应用场景
线性代数在很多领域都有应用,例如:
- 计算机图形学:三维图形的旋转、缩放和投影都可以用矩阵变换来表示。
- 机器学习:线性代数是机器学习中的基础,例如线性回归、主成分分析等算法都需要用到矩阵运算。
- 信号处理:信号可以用向量表示,线性代数可以用来处理信号的滤波、降噪等问题。
- 量子力学:量子态可以用向量表示,线性代数是量子力学的基础。
学习路线
线性代数的学习路线可以大致分为以下几个阶段:文章来源:https://www.toymoban.com/news/detail-784600.html
- 向量和矩阵基础:向量和矩阵的定义、加法、数乘、内积、外积等基本概念和运算。
- 线性方程组:高斯消元法、矩阵求逆、LU分解等方法求解线性方程组。
- 行列式和特征值:行列式的定义和计算方法,特征值和特征向量的定义和计算方法。
- 线性变换:线性变换的定义、矩阵表示、特征值和特征向量等概念。
- 向量空间:向量空间的定义、子空间、基和维数等概念。
要点分析
线性代数的重点在于理解向量空间、线性变换和矩阵等概念,并能够熟练地进行矩阵运算和求解线性方程组。以下是一些重要的要点:文章来源地址https://www.toymoban.com/news/detail-784600.html
- 理解向量空间的定义和基本性质,例如向量加法、数乘、内积、范数等。
- 理解矩阵的定义和基本运算,例如矩阵加法、数乘、乘法等。
- 熟练掌握高斯消元法、矩阵求逆、LU分解等方法求解线性方程组。
- 理解行列式的定义和计算方法,掌握行列式的性质和应用。
- 理解特征值和特征向量的定义和计算方法,掌握特征值和特征向量的性质和应用。
- 理解线性变换的定义和矩阵表示,掌握线性变换的基本性质和应用。
- 理解向量空间的子空间、基和维数等概念,掌握向量空间的基本性质和应用。
到了这里,关于线性代数-学习指引的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!