【学习笔记】【DOA子空间算法】4 ESPRIT 算法

4 ESPRIT 算法

4.1 算法原理

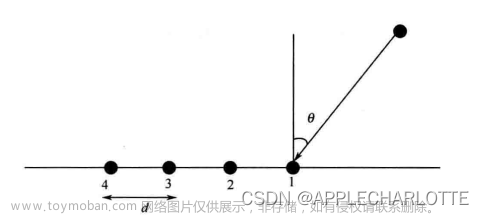
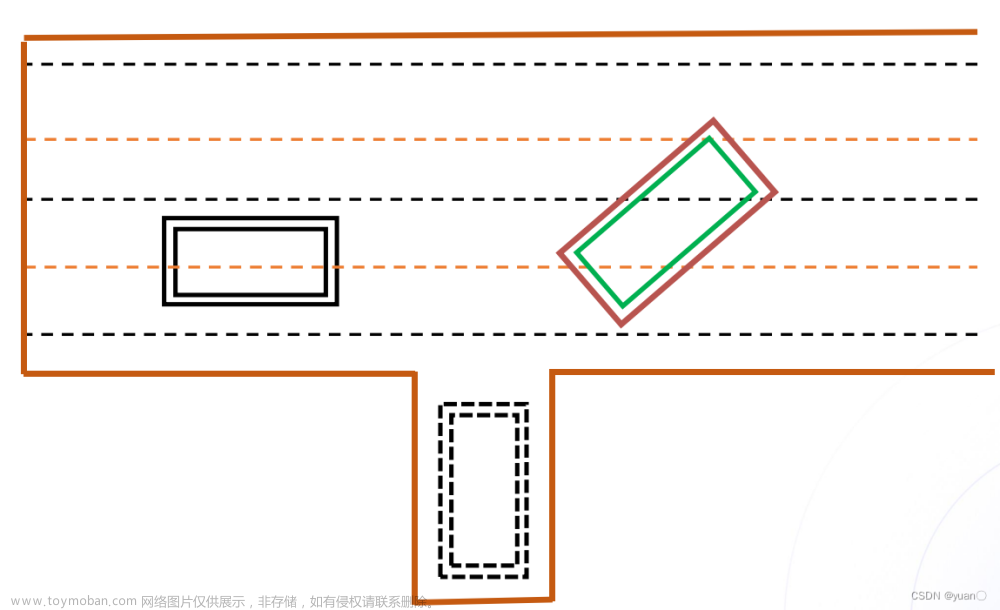
  ESPRIT 算法假设阵列传感器成对出现（即有一组平行的传感器），并且每对传感器之间有相同的位移 $\Delta$。这两组传感器的阵列接收向量分别表示如下：
$$\begin{array}{c}\begin{array}{rl}\mathbf{x}(t)& =\mathbf{As}(t)+{\mathbf{n}}_x(t)\\ \mathbf{y}(t)& =\mathbf{A}\Phi \mathbf{s}(t)+{\mathbf{n}}_y(t)\end{array}\end{array}$$
其中 $\mathbf{x}(t)$ 和 $\mathbf{y}(t)$ 为两个子阵列，该两个阵列的阵元数相同，且对应阵元之间的相位差相同；$\Phi$ 表示由阵列 $\mathbf{x}(t)$ 向阵列 $\mathbf{y}(t)$ 转换的矩阵，以 ULA 为例，则有：
Φ = diag ⁡ { exp ⁡ ( j 2 π Δ sin ⁡ θ 1 / λ ) , ⋯   , exp ⁡ ( j 2 π Δ sin ⁡ θ K / λ ) } \begin{equation*} \Phi = \operatorname{diag}\{\exp(j 2\pi \Delta \sin \theta_1 / \lambda), \cdots, \exp(j 2\pi \Delta \sin \theta_K / \lambda) \} \end{equation*} Φ=diag{exp(j2πΔsinθ1​/λ),⋯,exp(j2πΔsinθK​/λ)}​
  由该对平行传感器组成的总阵列接收向量 $\mathbf{z}(t)\in {\mathbb{C}}^{2M\times 1}$ 如下：
$$\begin{array}{c}\begin{array}{rl}\mathbf{z}(t)& =\left[\begin{array}{c}\mathbf{x}(t)\\ \mathbf{y}(t)\end{array}\right]=\overline{\mathbf{A}}\mathbf{s}(t)+{\mathbf{n}}_z(t)\\ & =\left[\begin{array}{c}\mathbf{A}\\ \mathbf{A}\Phi \end{array}\right]\mathbf{s}(t)+\left[\begin{array}{c}{\mathbf{n}}_x(t)\\ {\mathbf{n}}_y(t)\end{array}\right]\end{array}\end{array}$$
且总阵列接收矩阵为 $\mathbf{Z}=[\mathbf{z}(1),\cdots ,\mathbf{z}(T)]$，利用 $\mathbf{Z}$ 可以获得信号子空间 ${\mathbf{U}}_S\in {\mathbb{C}}^{2M\times K}$。
  信号子空间的一个特性就是与方向矢量矩阵所张成的空间是一致的，即 $\mathrm{span}(\overline{\mathbf{A}})=\mathrm{span}({\mathbf{U}}_S)$，因此必定存在一个唯一的非奇异满秩方阵 $\mathbf{T}$ 使得下式成立：
$$\begin{array}{c}{\mathbf{U}}_S=\overline{\mathbf{A}}\mathbf{T}\end{array}$$
且 ${\mathbf{U}}_S$ 同样可以分成上下两部分：
$$\begin{array}{c}{\mathbf{U}}_S=\left[\begin{array}{c}{\mathbf{U}}_X\\ {\mathbf{U}}_Y\end{array}\right]=\left[\begin{array}{c}\mathbf{AT}\\ \mathbf{A}\Phi \mathbf{T}\end{array}\right]\end{array}$$
由上式可以推导出：
$$\begin{array}{c}{\mathbf{U}}_Y={\mathbf{U}}_X{\mathbf{T}}^{-1}\Phi \mathbf{T}\end{array}$$
此时令 $\Psi ={\mathbf{T}}^{-1}\Phi \mathbf{T}$ 则有：
$$\begin{array}{c}{\mathbf{U}}_Y={\mathbf{U}}_X\Psi \end{array}$$
上式表明了：${\mathbf{U}}_Y$ 和 ${\mathbf{U}}_X$ 所张成的空间是一致的，即 $\mathrm{span}({\mathbf{U}}_X)=\mathrm{span}({\mathbf{U}}_Y)$，且 $\Phi$ 和 $\Psi$ 为相似矩阵，$\Phi$ 的对角元素是 $\Psi$ 的特征值。这意味着只需要求得 $\Psi$ 然后进行特征值分解即可：
$$\begin{array}{c}\Psi ={\mathbf{U}}_X^{†}{\mathbf{U}}_Y\end{array}$$
其中 $(\cdot {)}^{†}$ 表示伪逆。由前面的讨论可以看出，只要能估计出 $\Psi$，就能估计出 $\Phi$，同时可以得到到达角度。
  然而通常情况下只有一组传感器阵列 $\mathbf{X}=[\mathbf{x}(1),\cdots ,\mathbf{x}(T)]$，因此需要做的就是通过 $\mathbf{X}$ 构造 $\mathbf{Z}=[\mathbf{z}(1),\cdots ,\mathbf{z}(T)]$，对于 ULA 而言，第一组元素可以取 $M$ 个阵元中的 $1\sim M-1$ 个（前 $M-1$ 个），第二组元素可以取 $M$ 个阵元中的 $2\sim M$ 个（后 $M-1$ 个），则此时可以认为 $\Delta =-d$。
  具体来说，我们不需要直接构造 $\mathbf{Z}$，因为利用 $\mathbf{Z}$ 构造 ${\mathbf{U}}_S\in {\mathbb{C}}^{2M\times K}$ 计算量上较大；可以通过 $\mathbf{X}$ 构造 ${\mathbf{U}}_S$，然后分别取 ${\mathbf{U}}_S$ 的前 $M-1$ 个和后 $M-1$ 个组成 ${\mathbf{U}}_X\in {\mathbb{C}}^{(M-1)\times K}$ 和 ${\mathbf{U}}_Y\in {\mathbb{C}}^{(M-1)\times K}$。需要注意的是这两种构造方法是等价操作。

4.2 算法步骤

  ESPRIT 算法步骤如下（输入为阵列接收矩阵 $\mathbf{X}$）：文章来源地址https://www.toymoban.com/news/detail-784669.html

1. 计算协方差矩阵 $\mathbf{R}=\frac{1}{T}\mathbf{X}{\mathbf{X}}^H$。
2. 对 $\mathbf{R}$ 进行特征值分解，并对特征值进行排序，然后取得 $K$ 个较大特征值对应的特征向量来组成信号子空间 ${\mathbf{U}}_S$。
3. 分别取 ${\mathbf{U}}_S$ 的前 $M-1$ 行和后 $M-1$ 行形成 ${\mathbf{U}}_X$ 和 ${\mathbf{U}}_Y$。
4. 使用最小二乘法（或者完全最小二乘法）求解出 $\Psi$：
   $$\begin{array}{c}\Psi ={\mathbf{U}}_X^{†}{\mathbf{U}}_Y\end{array}$$
5. 对 $\Psi$ 进行特征值分解，得到 $K$ 个特征值 { z i : i = 1 , ⋯   , K } \{z_i:i = 1, \cdots, K\} {zi​:i=1,⋯,K}。
6. 利用下式求得角度 { θ i : i = 1 , ⋯   , K } \{\theta_i: i = 1,\cdots, K\} {θi​:i=1,⋯,K}：
   θ i = arcsin ⁡ ( − λ 2 π d arg ⁡ { z i } ) , i = 1 , ⋯   , K \begin{equation*} \theta_i = \arcsin\left(-\frac{\lambda}{2\pi d} \arg \{ z_i \} \right), i = 1, \cdots, K \end{equation*} θi​=arcsin(−2πdλ​arg{zi​}),i=1,⋯,K​

4.3 代码实现

% esprit.m
clear;
clc;
close all;

%% 参数设定
c = 3e8;                                              % 光速
fc = 500e6;                                           % 载波频率
lambda = c/fc;                                        % 波长
d = lambda/2;                                         % 阵元间距，可设 2*d = lambda
twpi = 2.0*pi;                                        % 2pi
derad = pi/180;                                       % 角度转弧度
theta = [-20, 30]*derad;                              % 待估计角度
idx = 0:1:7; idx = idx';                              % 阵元位置索引

M = length(idx);                                      % 阵元数
K = length(theta);                                    % 信源数
T = 512;                                              % 快拍数
SNR = 10;                                             % 信噪比

%% 信号模型建立
S = randn(K, T) + 0j*randn(K,T);                      % 复信号矩阵S，维度为K*T
% A = exp(-1j*twpi*d*idx*sin(theta)/lambda);          % 方向矢量矩阵A，维度为M*K
A = exp(-1j*pi*idx*sin(theta));                       % 2d = lambda，直接忽略不写
X = A*S;                                              % 接收矩阵X，维度为M*T
X = awgn(X,SNR,'measured');                           % 添加噪声

%% ESPRIT 算法
% 计算协方差矩阵
R = X*X'/T;
% 特征值分解并取得信号子空间
[U,D] = eig(R);                                       % 特征值分解
[D,I] = sort(diag(D));                                % 将特征值排序从小到大
U = fliplr(U(:, I));                                  % 对应特征矢量排序，fliplr 之后，较大特征值对应的特征矢量在前面
Us = U(:, 1:K);                                       % 信号子空间
% 角度估计
Ux = Us(1:M-1, :);
Uy = Us(2:M, :);

% 方法一：最小二乘法
% Psi = pinv(Ux)*Uy;
% Psi = linsolve(Ux,Uy);                                % Ux\Uy

% 方法二：完全最小二乘法
Uxy = [Ux, Uy];
Uxy = Uxy'*Uxy;
[U,D] = eig(Uxy);
[D,I] = sort(diag(D));
F = fliplr(U(:,I));
F0 = F(1:K, K+1:K*2);                                 % F0是F的左上角部分
F1 = F(K+1:K*2, K+1:K*2);                             % F1是F的右下角部分
Psi = -F0/F1;

[T,Phi] = eig(Psi);
Theta = asin(-angle(diag(Phi))/pi)/derad;             % 估计角度
Theta = sort(Theta).';
disp('估计结果：');
disp(Theta);

4.4 参考内容

1. Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on acoustics, speech, and signal processing, 1989, 37(7): 984-995.
2. 【知乎】ESPRIT算法的数理逻辑（DOA）（包含每一个细节）
3. 【CSDN】DOA算法2：ESPRIT算法
4. 【CSDN】【阵列信号处理】DOA估计算法

到了这里，关于【学习笔记】【DOA子空间算法】4 ESPRIT 算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！