云计算工作流调度

Cost-driven scheduling of service processes in hybrid cloud with VM deployment and interval-based charging

阅读笔记

首先，我们提出了一个更实用的混合云服务流程成本驱动调度模型，该模型在不降低VM部署弹性的情况下更精确地定义资源约束，并考虑了基于间隔的综合收费，包括计费周期和持续使用折扣。
其次，提出了一种改进的基于FWA（烟花算法）的方法来解决这一问题。在FWA框架[28,29]的基础上，设计了一种考虑任务间依赖关系的烟花表示，并提出了一种基于虚拟机部署和基于间隔充电的解码策略，将每个烟花映射到一个可行的调度解决方案。
此外，还设计了一种基于大都市接受准则的烟花更新策略，以降低计算复杂度，脱离局部最优。
与现有的工作相比，本文的贡献如下：
（1）为混合云中成本驱动的服务流程调度建立了一个更实用的模型。由此可见，在不降低虚拟机部署弹性的情况下，更精确地表述了混合云中的资源约束，从而正确地约束了搜索空间。此外，还考虑了计费周期和持续使用折扣等全面的间隔收费，通过合理增加虚拟机的持续使用来降低成本。
（2）改进烟花算法开发解决这个问题，其中具体表示和解码的烟花提出我们解决的问题（例如，考虑任务之间的依赖关系，虚拟机部署和间隔充电），和基于大都市接受标准烟花更新是用来提高效率和有效性。

本文的其余部分组织如下。在第二节中，提出了动机案例和问题陈述。第3节介绍了相关的工作。第4节介绍了初步的内容形式主义和形式模型。.第5节描述了我们的方法。第6节通过各种实验评估了我们的方法与其他方法的性能。第7节总结了论文，并探讨了未来的工作。

2.动机案例和问题陈述

在本节中，我们首先给出一个示例来演示混合云中的服务流程调度，这是对[30,31]中描述的一个示例的摘录和改编。

2.1.动机案例 (Motivation case)

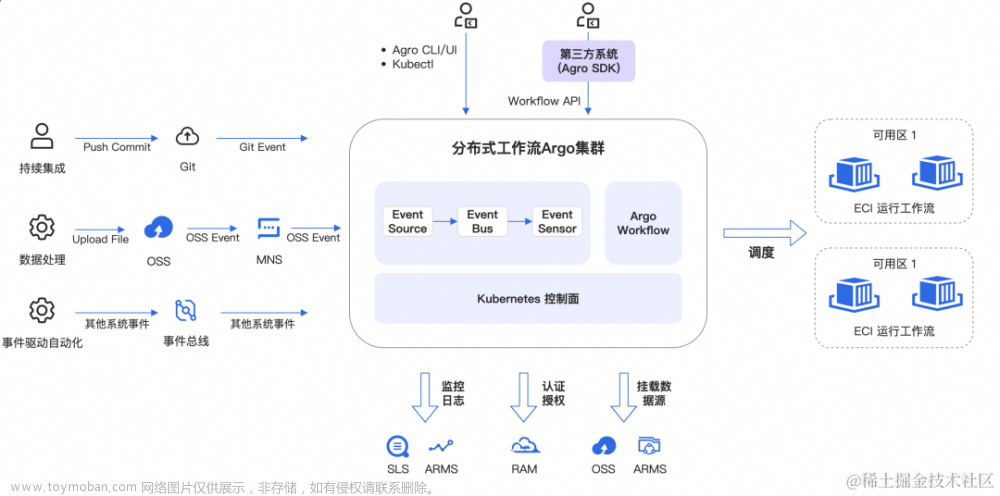
由两个并发工作流网组成的新产品开发的服务流程如图1所示。以WFN1为例。它由19个任务组成，包括从分析需求（t11）到制造模拟（t19），其中电弧显示了依赖关系。标记为cp1的制造商拥有两台物理机器，每台都有10个cpu和20GB内存，它们可以实例化到几种类型的vm。在这里，我们引用[10,32]来定义VM类型，而不同VM类型对每个任务的预期运行时的描述见表1.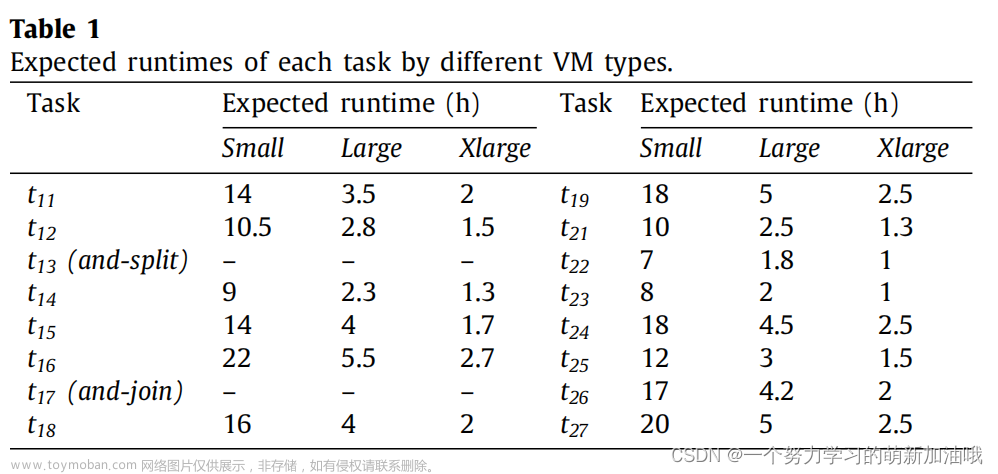

为了缩短产品上市时间，获得更大的市场份额，制造商cp1要求整个过程持续时间不能超过12h。然而，由于服务过程涉及到一些计算密集型的任务，如模拟和数据分析，因此资源无法以承诺的QoS来完成任务。为了确保及时执行，cp1将把其部分任务外包给外部公共云，这些外部公共云可以提供不同价格的VM类型，这就需要在混合云中进行服务进程调度。

近年来，许多研究人员解决了混合云中服务流程的调度问题，以降低QoS满意的用户成本。但是，他们很少考虑虚拟机部署和基于间隔的充电所造成的复杂性，这可能会导致不可行的解决方案和成本的增加。

(1) VM deployment

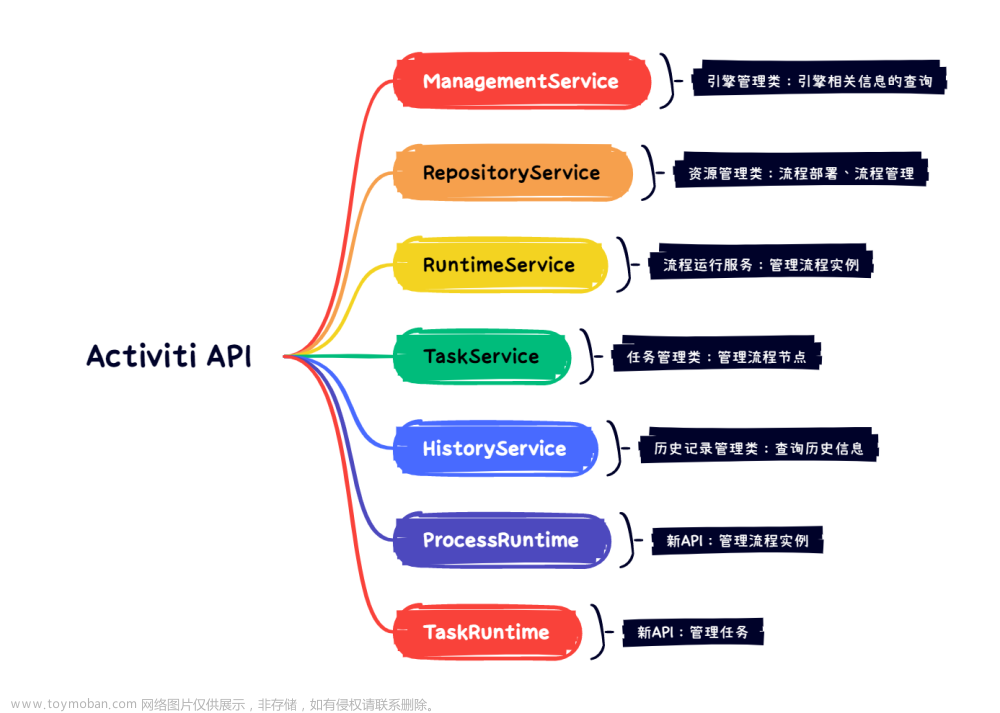
为了使虚拟机资源及其容量约束形式化，许多研究假设虚拟机是预先确定的。例如，它们定义了私有云中存在一个Xlarge类型VM和两个大型类型VM。但是，如图2所示，cp1的资源也可以实例化为两个Xmlarge类型vm，每个有8个cpu和15GB内存，或者4个大型类型vm，每个有4个cpu和7.5GB内存，可以同时实现4个任务。因此，预定义虚拟机可能会降低弹性。

为了增加弹性，一些研究定义了云机类型，并形式化了混合云中所有资源的容量约束。例如，它们形式化了私有云中的vm所需的资源不能扩展10个×2cpu和 20 × 2GB内存大小。因此，可以创建两个Xlarge类型虚拟机和一个大型类型虚拟机（假设应用的下降率为1），满足8×2+4≤20(cpu)和15×2+7.5≤40(GB)。然而，这是一个不可行的VM配置，因为除了一个Xlarge类型VM，没有由于8+4>10(CPUs)，PM不能同时托管一个大型类型VM。因此，只考虑所有资源的容量限制是不精确的。为了提供可行的解决方案，一旦VM在资源有限的私有云中运行，就应该明确地决定VM的部署。

（2）基于间隔的充电

此外，现有的研究很少全面考虑在云计算中广泛使用的基于间隔的充电。例如，腾讯是中国最有价值的科技公司之一，它为其部分云产品提供了三个价格细分市场，如下：[31]。
根据表2，计费周期为1小时，这意味着用户即使只使用了其中的一小部分，也要完全收取1小时的费用。假设任务t11是由一个大型类型的虚拟机实现的，其收费为每小时$0.1，因此用户必须支付4×0.1=$0.4，剩余时间为0.5h。然而，许多最近的研究要么在不考虑计费周期的情况下计算成本为0.35美元，要么在不利用尾部时间间隔的情况下将执行时间相加计算成本为0.4美元。由于任务的持续时间可能不是计费周期的整数倍，因此不考虑尾部的时间间隔可能会增加成本。
此外，它表明用户可以获得持续使用折扣，即他运行VM的时间越长，他能获得的折扣就越大。假设t12也被分配给了同一个VM。由于计费间隔增加到7小时，可以达到表2中的第二个价格部分，因此实施t11和t12的总成本为5×0.1×（7-5）×0.9×0.1=$0.68。然而，现有的研究很少考虑持续使用造成的价格折扣，因此不能通过合理增加租用虚拟机的持续使用来精确计算和降低成本。

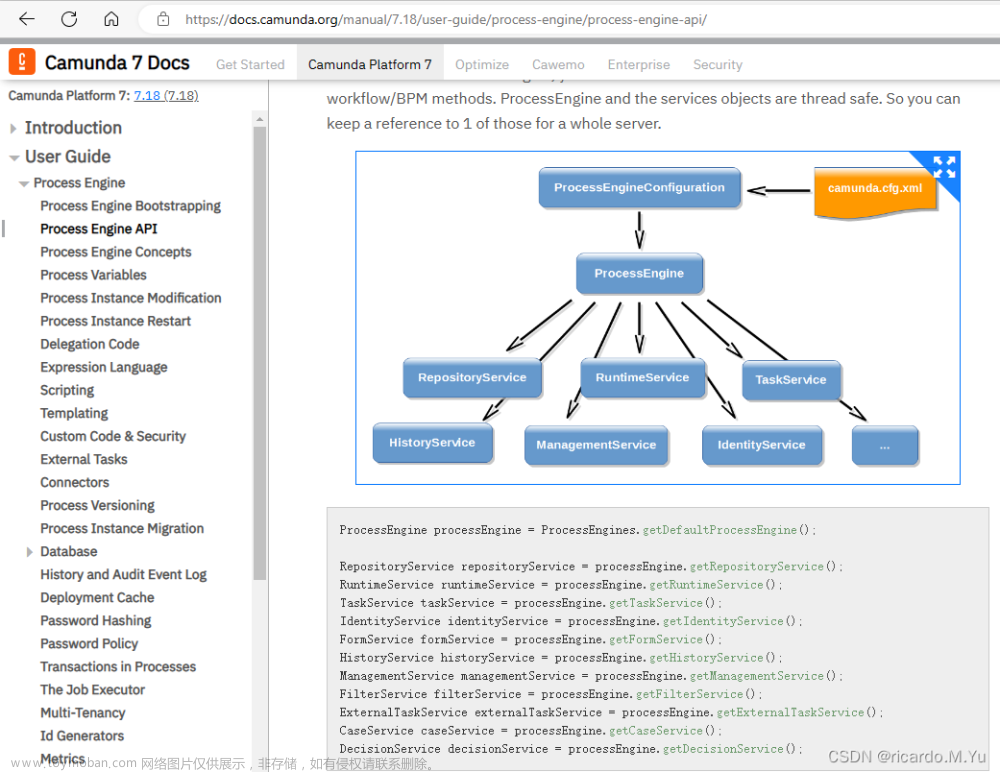
此外，由于基于间隔的收费，我们认为有必要制定一个计费计划来回答所分配的虚拟机，这在降低成本方面起着重要的作用。假设根据一个执行计划，t11和t14都是由大型虚拟机实现的。请注意，有两种方法来实现执行计划。如图3所示，计费计划I是分别为t11和t14租用两个大型虚拟机，而计费计划II是为这两个任务租用一个大型虚拟机。由于t11的计费间隔是4小时，而t14的计费间隔是3小时，所以计费计划I的成本是4×0.1+3×0.1=$0.7。假设t11和t14之间的空闲时间为0.5h，因此首选计费计划II，因为成本可以降低到5×0.1+（0-5）×0.9×0.1=$0.68。而如果空闲时间为1.5h，其成本将增加到5×0.1+（8-5）×0.9×0.1=$0.77，因此计费计划I是首选。

如本例所示，在混合云中做出调度决策不仅依赖于具有复杂依赖关系的任务，还依赖于私有云和公共云中的各种弹性资源。特别是提供多少和何时提供虚拟机的数量受到用户物理资源的限制，而基于间隔的充电起着重要的作用.
因此，为了以满意的QoS降低用户成本，需要对混合云与虚拟机部署和基于间隔的收费的服务流程调度问题进行适当的分析和解决。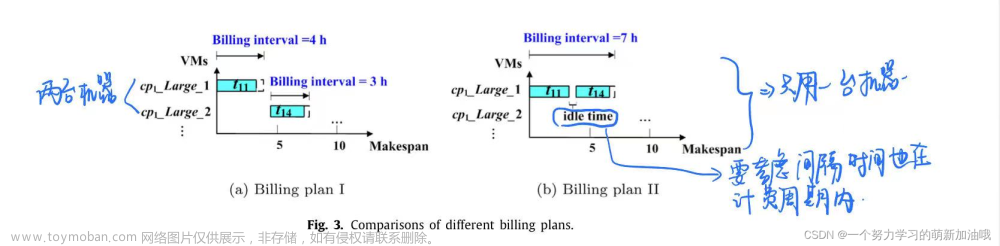

2.2.问题陈述

讨论的问题描述如下：
给定（1）一个私有云cp1和一组公共云ExCs，每一个都提供不同类型的虚拟机VS；
（1）cp1拥有一组物理机器PS，每个物理机都可以在其容量内托管不同类型的虚拟机；
（2）每个云采用基于间隔的收费，其中用户按计费周期数和持续使用折扣收费；
（3）安排一组任务，其中存在依赖关系和期限限制。

我们如何找到最佳的调度解决方案S来最小化用户的成本，它可以回答每个任务租用的VM，以及一旦虚拟机在私有云中运行，它被部署在哪个物理机器上？

3.相关工作

在本节中，我们将我们的方法与现有的混合云中服务流程的成本驱动调度[4,10-17]、考虑虚拟机部署的任务调度[18,19,33-36]和考虑基于间隔的收费[24–27]的任务调度的研究进行了比较。

3.1.混合云中服务流程的成本驱动调度

成本驱动的服务进程成本驱动调度是以最小的成本将一组依赖任务分配给资源的过程，这是云计算中最具挑战性的问题之一。与公共云或私有云中的调度不同，混合云中的服务进程的调度更为复杂，因为它不仅考虑了起源本身所拥有的“有限”资源，而且还考虑了公共云中的“无限”资源。目前，许多研究者已经解决了这个问题，并取得了很好的结果。

[11–13]提出了一些基于启发式的方法，一旦在私有云中没有满足任务的截止期限，任务将被分配给公共云。本文将问题形式化，并提出了一些基于元启发式的方法来提高计算的有效性。然而，上述研究都假设虚拟机是预先确定的。由于虚拟机可以被云中的物理资源弹性地实例化，因此预定义虚拟机将会减少搜索空间，从而减少了找到好的解决方案的可能性。

为了增加弹性，一些研究定义了虚拟机类型，每一个都可以提供不确定数量的虚拟机，并形式化的容量限制私有云分配虚拟机的资源需求不能超过所有可用资源的容量(例如，cpu总数)[10,16,17]。但是，由于是否可以创建虚拟机取决于特定物理机器的容量，上述方法会使搜索空间太大，从而导致大量不可行的解决方案。为了精确地绑定搜索空间，必须考虑能够满足私有云中物理机器的资源约束的虚拟机部署。

等等。。。

4.初步的形式主义和形式化模型

在本节中，我们首先在第4.1节中对我们的问题的关键概念提出一些初步的形式主义。然后，在第4.2节中讨论了形式化模型。为了清晰起见，本节中使用的所有符号都在手稿的开头以命名法的形式进行了总结。

本文根据混合云中常用的资源模型定义了资源模型。在这个资源模型中，一方面，私有云由一组物理机器组成，每台物理机器都有有限的CPU和内存大小，并且可以在其资源限制范围内托管各种VM类型的实例。另一方面，存在一组公共云，每个公共云都有无限的资源，可以提供无限数量的各种类型的虚拟机。此外，资源以互斥的方式访问，这意味着每次按照FIFO的顺序只能执行一个任务。此外，我们遵循云中使用的典型网络模型，其中每个虚拟机都有网络带宽，其网络容量足以完成任务。一旦任务产生数据，它就从分配的虚拟机转移到其直接后继者分配给的虚拟机，从而实现具有依赖关系的任务。

在混合云中的服务进程的调度问题中，在私有云和公共云中同时调度一组依赖的任务，并制定执行计划，为每个任务分配了哪个VM。在本节的其余部分中，我们只给出了本文中使用的一些新概念，而省略了一些一般的定义（如混合云、执行计划），它们可以参考[10]

首先，基于计费周期和持续使用折扣的间隔收费定义如下：

Definition 1 (Interval-based Charging).间隔收费

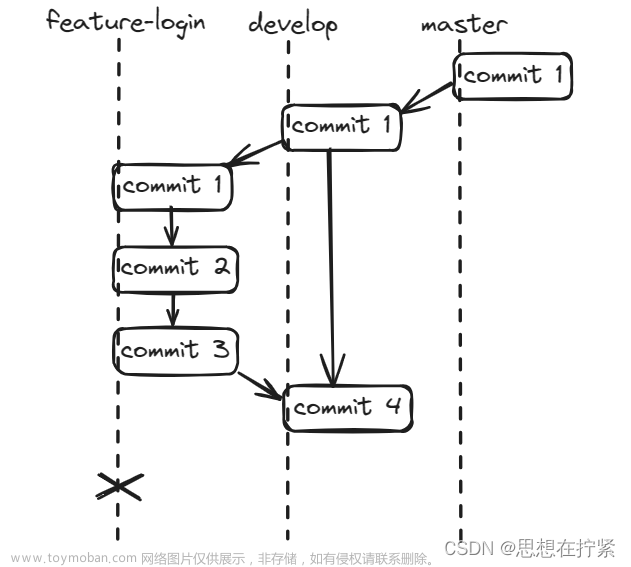
根据表2，计费周期可以形式化为b=1。另外，计费函数F(t)如图4所示，其中c是一种特定VM类型的单价，持续使用间隔分别为[0、5)、[5、10)和[10、+∞)。
此外，为了利用尾部时间，增加持续使用，有必要对所有分配的虚拟机制定计费计划：

定义2（虚拟机的计费计划）。考虑一个混合云CS和一组要计划为TS的任务。计费计划被定义为BP={cpk、vmtkv、BSkv、TSkv|cpk∈CS、TSkv⊂TS}，其中：（1）cpk和vmtvk代表第k云提供商和其提供的VM类型；（2）BSvk={BSvk1，BSvk2，…每项BSvkq代表第qVM的计费间隔；（3）TSvk={TSvk1，TSvk2，…每个项TSvkq代表第qVM执行的任务集。此外，只有当私有云提供的每个虚拟机都可以部署在物理机器上时，调度解决方案才可行，因此部署计划的定义如下：

定义3（虚拟机的部署计划）

考虑私有云cp1中的一组物理机器PS，以及一组已分配的vm，其计费间隔为BS。部署计划定义为

其中：（1）vmtv1表示私有云提供的第一种VM类型；（2）BSv1q表示第一种VM的计费间隔；（3）pmp是部署在VM上的物理机器。
重新考虑第2.1节中的例子。计费计划被正式化为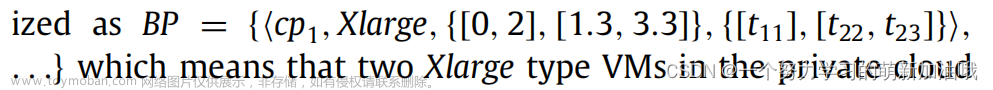

这意味着在私有云中租用了两个Xmarge类型的vm，一个是任务t11，计费间隔为[0,2]，另一个是任务t22和t23，计费间隔为[1.3,3.3]。此外，虚拟机的部署计划可以形式化为DP={Xlarge，[0,2]，pm1，……这意味着私有云提供的第一个Xmalage类型VM部署在pm1上。

请注意，定义2∼3也可以合并为一个定义，它由任务分配、虚拟机的计费间隔及其部署组成。在本文中，我们将它们分开，使其更加清楚。

4.2.基于虚拟机部署和基于间隔计费的混合云服务流程调度的形式化模型

在一个真实的商业世界中，许多参数都会对成本产生影响。
本文考虑了计算（处理）成本，即根据用户使用的时间间隔和云提供商的收费价格进行收费。特别是，我们的模型在计算计算成本时，综合考虑了计费周期和持续使用折扣。由于每个分配的虚拟机的计费间隔可能覆盖多个价格段，因此可以根据计费功能获得其成本，如等式所示 (1)
总之，我们所讨论的服务流程调度的形式化模型可以定义如下：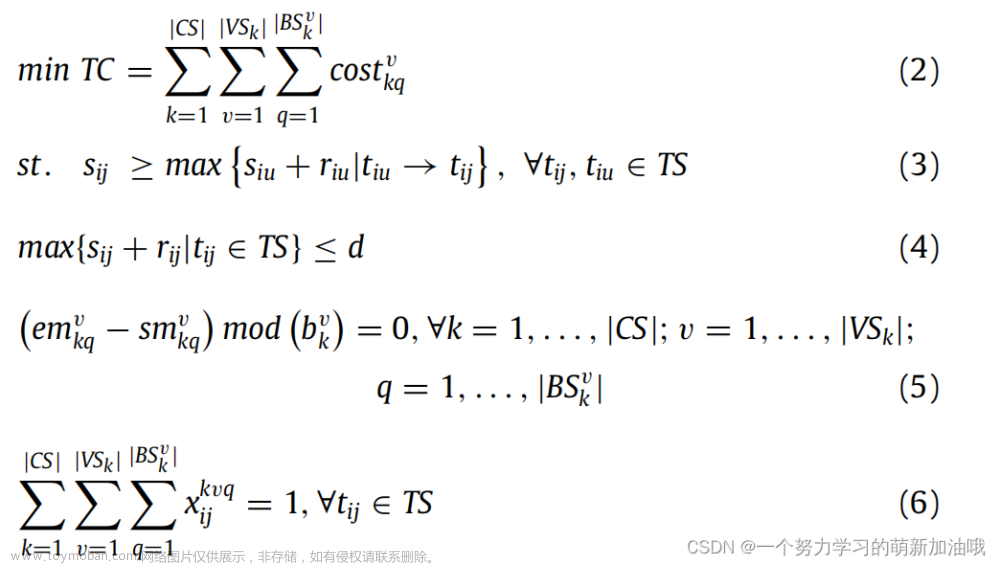
决策变量v=
和ztwij可以回答混合云中的哪个虚拟机以及何时分配给每个任务；

目标（2）旨在最小化用户的总成本。约束（3）∼（4）定义了依赖关系关系和截止日期约束。约束（5）显示虚拟机的计费间隔是计费周期的整数倍。约束（6）表示每个任务都被分配给一个VM类型的实例。约束（7）表示每个虚拟机只能同时运行一个任务，每个任务必须在分配的虚拟机的计费间隔内执行。约束（8）保证私有云提供的每个虚拟机都恰好部署在一台物理机器上。
应用约束（9）∼（10）可以确保cpu和内存大小不会超过私有云中每个物理机器的可用资源限制。“公式”。（11）∼（14）给出了决策变量的定义.

与现有的研究成果相比，本文从以下几个方面提出了一种更实用的混合云服务流程成本驱动调度模型：

（1）我们的模型考虑了在商业世界中广泛使用的基于间隔的收费。我们不仅定义了约束（5）来形式化每个虚拟机所基于的计费周期，而且还定义了等式。（1）∼（2）来计算考虑持续使用折扣的总成本。此外，我们将每个虚拟机的计费间隔作为决策变量，将约束（6）∼（7）形式化，将任务分配给虚拟机，有助于精确计算成本，并通过合理增加虚拟机的持续使用来降低成本。

(2)我们的模型考虑了虚拟机的部署计划，其中我们定义了等式对虚拟机部署的决策变量（14）和使用约束（8）∼（10）来形式化资源约束。它可以在不降低弹性的情况下更精确地描述混合云中的资源约束，有助于正确地约束搜索空间。此外，它还可以给出关于VM部署的明确决策，这有助于私有云配置其物理资源。

5.一种改进的基于烟花烟花的调度算法

我们所解决的问题包含各种决策变量和非线性约束。为了在合理的计算时间内获得令人满意的解，我们采用了能够在收敛性和多样性方面实现良好平衡的元启发式方法,
受夜间天空爆炸的启发，2010年[28]提出了一种新的元启发式方法烟花算法(FWA)。它模拟了烟花的爆炸过程，其中烟花意味着一个解决方案，而产生的火花代表了一组潜在的解决方案，填补了周围的烟花空间。FWA的关键原理是，高适应度的烟花可以在一个小的社区内产生大量的火花，这有助于提高收敛速度。同时，低适合度烟花在大范围内产生少量火花，以提高勘探能力，保持[28,29,37,38]的多样性。这些吸引人的特性表明，它非常适合我们所解决的问题。针对问题的特殊性，提出了一些基于FWA框架的问题相关策略：

一种新的烟花表示，它表示满足任务之间依赖关系的秩值的可行列表。

一种新的烟花解码策略，它可以将烟花映射到一个考虑虚拟机部署和基于间隔的充电的可行解决方案

一种基于大都市验收标准的新型烟花更新策略，可以摆脱传统FWA容易陷入的局部最优状态，提高了计算效率。

综上所述，我们基于FWA的混合云中基于VM部署和基于间隔的收费(FWAPS_VI)的服务流程调度算法的流程图如图5所示。上述改进的策略将在第5.1节∼5.3中详细阐述。整个过程在5.4节中设计，动机案例被用来说明如何通过5.5节中的方法找到最佳解决方案。

5.1在任务之间考虑依赖关系的烟花表示

一个烟花通常被编码到一个位置列表中。请注意，这样的位置列表不能直接用于调度问题。根据[16,17]中的排序顺序值(ROV)规则，可以将其进一步转换为任务的排序值，其中将值较小的任务首先分配给资源。然而，[16,17]只关注独立的任务。考虑到任务之间的依赖关系，我们之前的研究[10]设计了一种新的表示方法，其中一个变量不断更新，以记录准备好的任务。但是，它不能处理由实数组成的位置列表。

针对上述方法，算法1提出了一种针对烟花的混合表示策略。

根据它，在任意k时间，给式得到的任务分配一个秩值k。（15），通过轮盘赌选择策略[2]具有高概率选择最高位置值或小概率的任务，以增加多样性(L3∼L4)。此外，只有在分配了一个任务时，才能考虑其后继任务，以保证每个任务的秩值必须大于其前一个任务的秩值(L5∼L6)。
其中，tij(k)是分配给第k个等级值的任务。STP是一组可以随时安排好的任务。fwij为任务tij的位置值。P0是一个预设的阈值。rand（0,1）是在（0,1）范围内随机生成的一个分数。Rou（·）是指轮盘赌的选择策略。

--------------------------------------------------------插入轮盘赌的定义和计算方式----------------------------------------------------------------------------------

Proportionate Roulette Wheel Selection

此轮盘赌选择策略，是最基本的选择策略之一，种群中的个体被选中的概率与个体相应的适应度函数的值成正比。我们需要将种群中所有个体的适应度值进行累加然后归一化，最终通过随机数对随机数落在的区域对应的个体进行选取，类似赌场里面的旋转的轮盘。
轮盘赌法是一种常用的随机算法
其目的，是为了让个体被选择的次数，遵循个体在总体中的适应度及选择概率。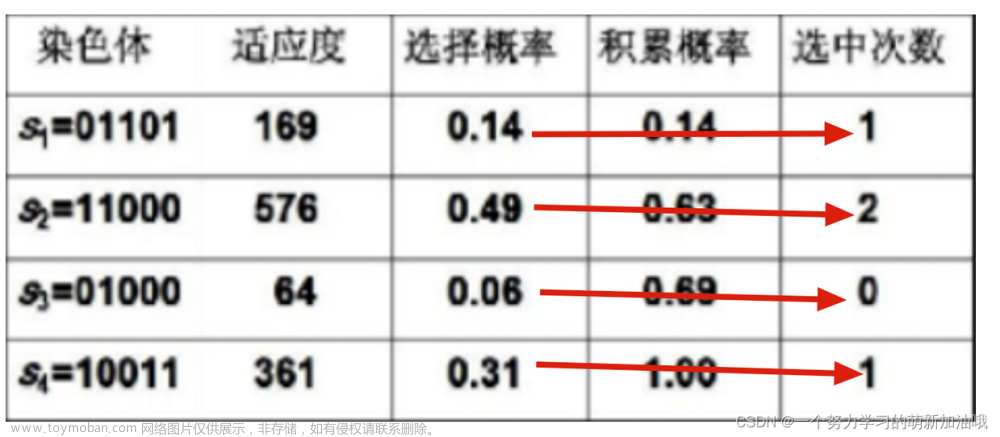

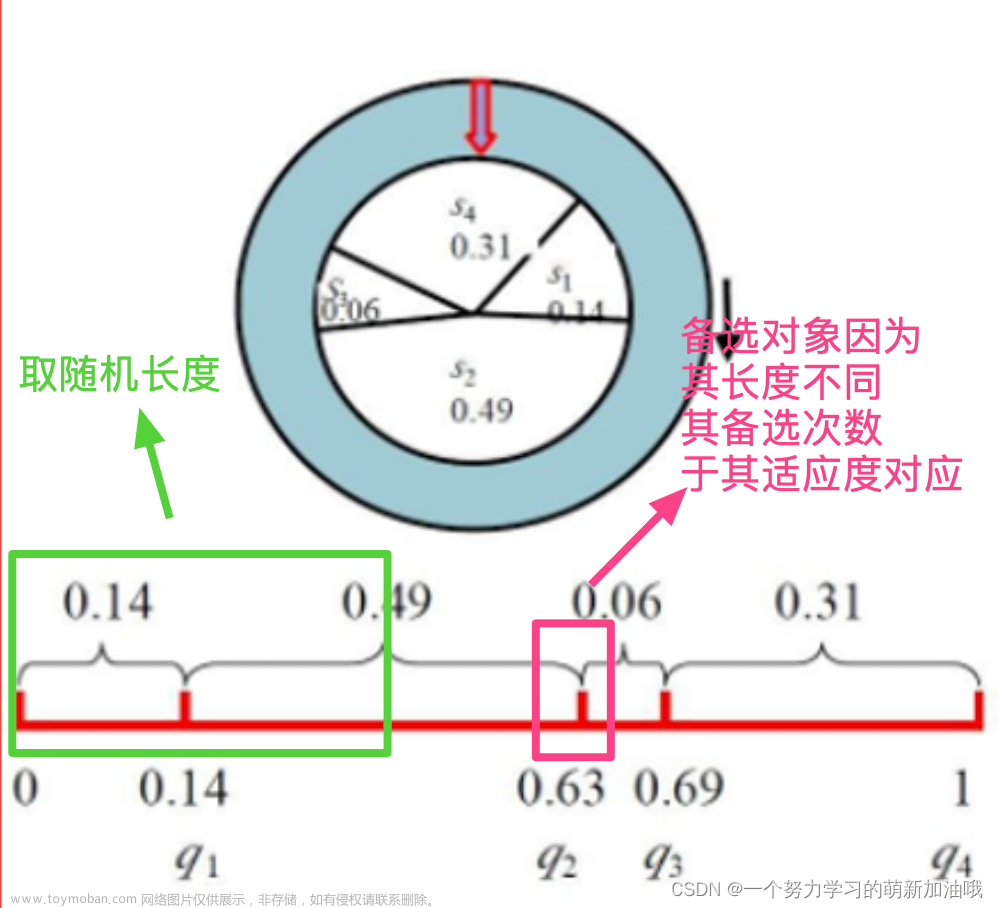
当然，处于计算机精度的考量，使用小数计算可能会导致种群概率总和小于或大于1，在面对海量数据的情况下，这种微小的差距可能带来难以想象的后果，所以我们也可以使用适应度和总适应度代替个体被选概率和总概率
----------------------------------------轮盘赌介绍结束----------------------------------------------------------------------------------------------------------

以第2.1节中的调度问题为例。如图6所示，由于需要14个任务，所以首先将烟花编码为长度为14的位置列表。接下来，算法1运行如下：首先，初始化STP={t11，t21}，这是WFN1和WFN2的启动任务。第二，假设随机分数不大于0.8，表示为预设阈值p0，则选择位置值最高的任务t21，否则，t11的选择概率为0.63/（0.63+0.72）=0.46，而t21的选择概率为0.54。假设选择了t21，因此我们可以得到rv[t21]=1，并更新STP={t11，t22}。重复上述过程，我们可以得到图6中所有任务的秩值。

5.2.解码烟花 考虑虚拟机部署和基于间隔的计费

在评估之前，每个烟花都应该被解码为一个调度解决方案。在我们之前的研究[10]中，我们将现有虚拟机的数量初始化为零。每次，分配给任务的现有虚拟机和每种VM类型的新虚拟机都被视为候选任务，因此一个任务以最小的成本贪婪地分配给一个合理的虚拟机。但是，这种方法没有考虑到基于间隔的充电和虚拟机部署，并且为每个任务迭代所有候选虚拟机是很耗时的。为了克服这些缺点，我们提出了一种新的基于启发式的策略来解码烟花到一个可行的解决方案，这在以下几个方面创造了新颖性：
1.设计了一种基于区间收费的成本计算方法，该方法可以精确地计算出考虑基于区间收费的特定虚拟机实现任务的成本。
2.•对于私有云提供的每个虚拟机，都设计了一种虚拟机部署方法来找到一个可行的物理机器来托管虚拟机。
3.•在此基础上，设计了一种新的解码策略，可以将任务分配给考虑资源优先级的虚拟机，从而降低计算复杂度，提高资源利用率。为了更清楚，我们使用算法2∼3来显示前两点，然后在算法4中给出了我们的解码策略。

（1）考虑基于间隔的收费的cost

要计算通过特定虚拟机实现任务的成本，首先要获得任务的计费间隔。对于新虚拟机，它的计费间隔从任务开始时间开始，它是计费周期的整数倍，不小于任务的执行时间。相比之下，对于之前已分配给任务的现有虚拟机，新添加的计费间隔从上一个计费间隔的结束时间开始，它是计费周期的整数倍。一旦获得了计费间隔，就可以计算出由该任务引起的附加成本。总之，所述过程如算法2所示。

（2）决定一个可行的VM部署

请注意，只有当一个PM有足够的资源来托管VM时，才能在私有云中创建VM。在本文中，我们提出了算法3来运行虚拟机部署。如L1∼L5（下面算法中步骤1到5）所示，如果VM是新创建的，则认为所有可用的PM都可以找到满足资源需求的可行的。而如果是现有的虚拟机，情况会更加复杂，因为VM必须部署在一个PM上。因此，考虑以下两种情况(L7∼L13)：一旦部署VM的PM有足够的资源，则首选；否则，认为所有其他PM都可以找到可行的。

（3）考虑资源优先级将任务分配给虚拟机

为了避免对所有计算复杂度较高的虚拟机进行迭代，提高持续使用间隔，设计了三种资源优先级。
首先，首选已分配给该任务的直接前辈的虚拟机。由于虚拟机可以不需要等待地继续执行任务，因此充分利用由计费周期造成的尾部时间，增加持续使用间隔是有帮助的。
其次，一旦没有将属于第一优先级的虚拟机分配给任务，搜索范围将扩大到之前已分配给任务的所有虚拟机，从而增加现有虚拟机的持续使用间隔。否则，将考虑所有新创建的VM类型的实例，以保证为该任务找到一个可行的VM。

总之，我们提出了算法4，将烟花解码为一个调度解决方案，其中任务根据烟花定义的等级值进行调度。每次都获得一个第个秩值的任务，并贪婪地将其分配给一个考虑资源优先级的虚拟机。特别是，一旦分配了一个新的虚拟机，它就会成为一个现有的虚拟机，并将其作为后续任务的候选对象。

以图6中的烟花表演为例。假设t16现在已经准备好调度，并且有两个现有的虚拟机已经分配给任务。
首先，获得三种资源优先级，分别是分配给其直接前身t12的VM cp1_Xlarge_1，另一种分配给其他前身任务的虚拟机，以及云中每种VM类型的新虚拟机。其中，首先考虑的是cp1_Xlarge_1。由于cp1_Xlarge_1的原始计费间隔为[0,4]，尾部间隔为0.5h，因此根据算法2，新增的计费间隔为[4,7]，成本为0.672美元。此外，算法3表明，虚拟机可以继续部署在第二台物理机器上。因此，我们可以将解决方案更新为EP=…，t16，cp1，Xlarge，3.5；BP=…，cp1，Xlarge，{[0,7]}，{[t11，t12，t16]}和DP=…，Xmarge，[0,7]，pm2。此外，在4到7的时间段内，pm2的可用cpu和内存大小被更新为10−8=2cpu和20−15=5GB。

5.3 根据大都市验收标准（based on Metropolis acceptance criterion）更新烟花表演

在随机生成一个初始烟花种群后，会更新它们，以找到最佳解决方案。根据FWA的框架，在每次迭代中，首先计算火花的数量及其振幅，以控制高适合度烟花在一个小区域内产生更多的火花，而低适合度烟花在一个大范围区域内产生更少的火花。其次，由爆炸或高斯算子产生一组火花，其中随机选择一些位置，并根据爆炸的振幅或高斯突变率更新其值。考虑到我们使用与[28]相同的策略来产生火花，为了清晰起见，本文省略了它们。详情请参考[28]。

一旦火花产生，烟花通常会通过分类所有的烟花和火花来更新。需要注意的是，这种方法非常耗时，因为需要排序大量的候选解，而且很容易陷入局部最优，因为在一个小的局部空间中有太多好的解会加剧不成熟的收敛。为了降低计算复杂度，逃离局部最优，我们采用大都市验收准则**[39]**来设计烟花更新策略

首先，获得每个烟花的最佳火花。第二，根据等式计算接受率 (16).一旦其目标值优于烟花的目标值，接受比等于1，从而替换烟花；否则，只有当随机小数大于接受比时，才会替换烟花，以便更广泛地搜索全局最优解。在搜索过程中，温度根据冷却速度逐渐降低，以模拟冷却概率的缓慢降低在探索解决方案空间时接受更差的解决方案。

综上所述，基于大都市验收准则的烟花更新流程见算法5。首先，由算法1和算法4生成并解码一组火花，从而得到一组潜在的解(L1∼L8)。其次，在火花火花中找到最佳的解决方案，并根据大都市验收标准(L9∼L13)更新烟花。

以第2.1节中的调度问题为例。如图7所示，假设一个烟花为fw=[0.63,0.68，……]，目标值为$10.656。我们首先计算 ne=3的爆炸火花数，这意味着产生三个新的爆炸火花。以爆炸火花es1为例。假设随机选择第2、第5、第7个维度，从而更新这些维度的位置值。同样地，用高斯突变替换其部分位置值也会产生高斯火花。在得到火花后，我们可以找到其中目标值为15.832美元的最佳解。由于它比fw差，所以用等式进一步计算了接受概率（16）为0.94。因此，一旦一个随机生成的分数小于0.94，烟花fw就会被更新。

5.4.我们的方法的整个过程

算法6展示了基于FWA的混合云VM部署和基于间隔的充电(FWAPS_VI)算法的过程。在初始阶段，就产生了一群初始烟花(L2∼L5)。对于每个烟花，首先随机生成位置列表，并通过算法1得到任务的秩值。此外，算法 4 解码每个烟花成调度解，这样我们就可以计算出烟花的客观值。 在迭代阶段（L6∼L11），烟花由算法 5 不断更新。在每个迭代，首先产生一组火花，然后是烟花根据 Metropolis 验收标准进行更新。一旦停止条件（例如，最大迭代时间）是满意，我可以输出最好的解决方案。

1. 假设有N个任务要调度，V是每个云提供的VM类型，P是私有云中的物理机器的数量。我们的算法由初始种群生成和迭代阶段组成，其复杂度分析如下：
   

   在初始阶段，由于烟花表示需要一个排序算法，在最坏的情况下，所有任务都是并行结构，其复杂度为O（Nlg(N)）。此外，为了解码烟花，在最坏的情况下，每个任务都被分配给由私有云提供的新虚拟机，复杂度为O(N(V+N)P)。最后，生成Gpop烟花，因此初始阶段的整体复杂度是O(Nlg(N)Gpop)+O((NVP+N2P)Gpop)=O((NVP+N2P)Gpop)。在迭代阶段，由于每个火花都需要表示和解码，因此其复杂性分别为O(Nlg(N))和O((NVP+N2P))。

2. 在所有的火花产生后，根据复杂度为O(E)的标准，其中E为火花的最大数量。总而言之，更新烟花的复杂性是O(Nlg(N))+O((NVP+N2P))+O(E)=O((NVP+N2P))。由于要生成的烟花的数量最大，迭代阶段的复杂性是O((NVP+N2P)最大)。结果表明，迭代阶段的复杂度最大。由于Maxiter和Gpop是常数，所以在最坏的情况下，我们的方法的总体复杂性是O(NVP+N2P)。请注意，根据我们定义了三种资源优先级的解码策略，大多数任务可以通过迭代少量的vm而不是所有任务来调度，因此实际计算复杂度比最坏情况下要低得多。文章来源地址https://www.toymoban.com/news/detail-785305.html

5.5.在动机案例中的应用

到了这里，关于云计算工作流调度的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！