Tracking-KCF Algorithm
注:本文涉及的算法的代码实践已上传至GitHub,恳求大佬们指点!^ _ ^
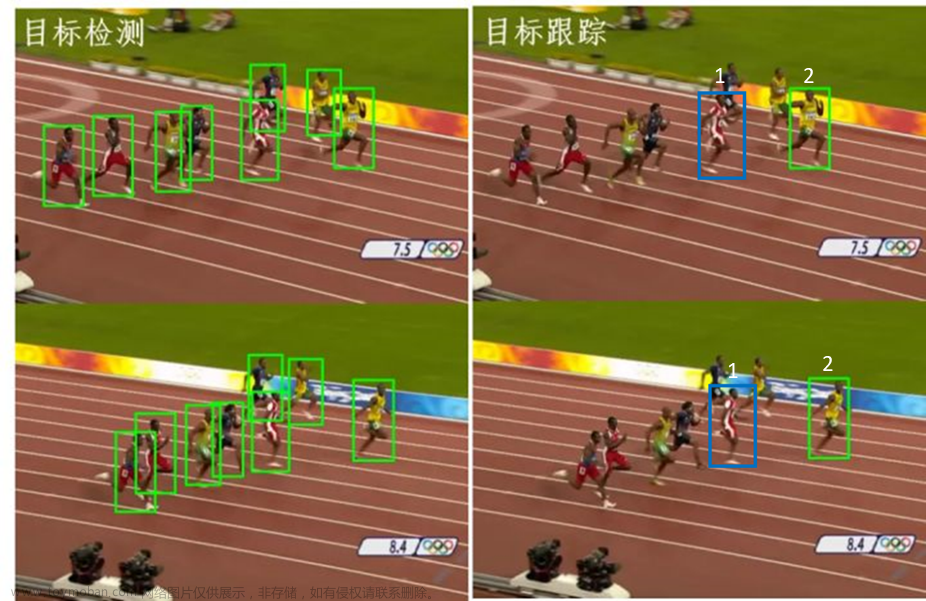
1. 目标检测跟踪与算法背景概述
目标跟踪任务在许多的计算机视觉系统中都是极为关键的一个组成部分。对于任意给定的一个初始图像的Patch(Filter滑过的区域),目标跟踪任务的目的在于训练一个分类器来将待跟踪的目标与它所处的环境区分开,为了能够在后续帧中能继续检测到这个目标,分类去需要能够在很多位置上都能进行详尽的评估,同时在滑动的过程中都会提供一个新的图像Patch来帮助提升模型的性能。
在上述任务中,我们将感兴趣的对象——即待追踪的目标称作正样本(positive samples),将目标所在的环境或者背景称作负样本。一幅图像中包含的负样本数量几乎是无限的,在达到合并尽可能多的样本和保持较低的计算量之间的平衡上,前人作出了很多尝试。KCF算法中,引入了轮转矩阵(circulant matrices)这一工具来合并大量的样本,实现了一个基于“核岭回归”的跟踪器(tracer),该跟踪器可以认为是一个核化版的线性相关滤波器(Linear Correlation Filter )。
Correlation Filter(CF)源于信号处理领域,其用于tracking方面的想法是:相关是衡量两个信号相似值的度量,如果两个信号越相似,那么其相关值就越高。在tracking的应用里,设计一个滤波模板,利用该模板与目标候选区域做相关运算,最大输出响应的位置即为当前帧的目标位置。
用数学语言来表述, x x x表示一幅图像, w \mathcal{w} w表示相应的滤波模板, y y y表示模板与相关候选区域进行相关运算后的相应输出,则有如下关系: y = x ⊗ w y=x\otimes\mathcal{w} y=x⊗w,为减小计算量,可将 x , y , w x,y,\mathcal{w} x,y,w分别转换到其傅里叶空间后计算点积,即 y ^ = x ^ ⋅ w ^ ∗ \hat{y} = \hat{x}· \hat{\mathcal{w}}^* y^=x^⋅w^∗。相关滤波的任务则是寻找最优的滤波模板 w \mathcal{w} w。
目下以相关滤波类的方法和深度学习方法为代表的判别类模型方法效果普遍好于生成模型,其显著特点是分类器的训练过程中运用到了前景与背景信息,分类器的任务专注于区分前景与背景。Kernelized Correlation Filter(KCF)是相关滤波方法中的典型算法,该方法的一般流程是:在跟踪的过程中训练一个目标检测器,使用目标检测器去检测下一帧预测位置是否是目标,然后再使用新检测结果去更新训练集进而更新目标检测器。
2. HOG特征
KCF算法中使用了图像的HOG特征替代了传统跟踪器所用的灰度特征。
HOG特征全称为Histogram of Oriented Gradients,即方向梯度直方图。作为一种图像的特征描述子(图像的一种表示,通过提取有用的信息并扔掉多余的信息来简化图像),HOG特征将一张大小为 w i d t h × h e i g h t × c h a n n e l s width \times height \times channels width×height×channels的图像转化为一个长度为 n n n的特征向量,例如输入图像大小为 64 × 128 × 3 64 \times 128 \times 3 64×128×3,HOG特征的输出为长度 3780 3780 3780的向量。HOG特征的计算过程如下:
(1)图像预处理
最早提出的HOG特征通过在一张 64 × 128 64 \times 128 64×128的图像上计算得到,预处理的操作要求图片保持1:2的横纵比,原文中提及的 γ \gamma γ矫正已知其增益效果较小,不再考虑。
(2)计算梯度图
首先计算图像的水平方向梯度
g
x
g_x
gx和竖直方向的梯度
g
y
g_y
gy,以如下公式来计算梯度的强度值
g
g
g和梯度方向
θ
\theta
θ:
g
=
g
x
2
+
g
y
2
θ
=
a
r
c
t
a
n
g
x
g
y
g=\sqrt{g_x^2+g_y^2}\\ \theta = arctan \frac{g_x}{g_y}
g=gx2+gy2θ=arctangygx
同时梯度方向有如下的性质:
θ
∈
[
0
,
π
]
\theta \in [0,\pi]
θ∈[0,π]。
(3)计算梯度直方图
这一步中,首先将图像分割成多个 8 × 8 8 \times 8 8×8的cell,在这些cell中计算梯度直方图。(2)中计算的每个像素点的位置处包含了2个值: g 和 θ g和\theta g和θ,一个cell就保存了128个值,单个像素的梯度信息往往包含了噪声,采用 8 × 8 8 \times 8 8×8的图片块表示后能够是的直方图对噪声不敏感。
由(2)的性质,将0-180度分成9个区间:0,20,40,…160,之后统计每个像素点所在的区间——将这个区间命名为bin,采取的原则是对每个像素点处的 g g g值,按 θ \theta θ的比例将 g g g分配给相邻的bin,如下图所示。
最终统计得到如下图所示的直方图:
(4)对 16 × 16 16 \times 16 16×16大小的Block进行标准化
标准化(Normalization)也称归一化,即将每个向量的分量除以向量的模长。Block选取示意图如下:
(5)得到HOG向量
将(4)中计算的单个Block的向量连接起来得到整个图片块的最终的特征向量,其中可以由这样的认识:每个16×16块由36×1向量表示。
OpenCV中封装了提取HOG特征的类HOGDescriptor,实现过程中只需构造一个hog对象来实现,见于HOG.py文件中的构造方法:
def __init__(self, winSize):
self.winSize = winSize
self.blockSize = (8, 8)
self.blockStride = (4, 4)
self.cellSize = (4, 4)
self.nbins = 9
self.hog = cv2.HOGDescriptor(winSize,self.blockSize, self.blockStride,self.cellSize, self.nbins)
3. 傅里叶变换
3.1 傅里叶变换概念简述
傅里叶变换(Fourier transform,FT)是一种线性积分变换,用于函数(应用上称作“信号”)在时域和频域之间的变换,在物理学和工程学中有许多应用,其作用是将函数分解为不同特征的正弦函数的和,如同化学分析来分析一个化合物的元素成分。对于一个函数,也可对其进行分析,来确定组成它的基本(正弦函数)成分。
经过傅里叶变换生成的函数 f ^ \hat {f} f^称作原函数 f f f的傅里叶变换,应用意义上称作频谱。在特定情况下,傅里叶变换是可逆的,即将 f ^ \hat{f} f^通过逆变换可以得到其原函数 f f f。通常情况下, f f f是一个实函数,而 f ^ \hat{f} f^ 则是一个复数值函数,其函数值作为复数可同时表示振幅和相位。高斯函数是傅里叶变换的本征函数(也称固有函数,即对已定义的函数空间中任意一个非零函数 f f f 进行变换仍然是函数 f f f或者其标量倍数的函数。更加精确的描述就是 A f = λ f \mathcal{A}f = \lambda f Af=λf其中 λ \lambda λ是标量,它是对应的特征值),即若一个函数(或分布)在真实空间中是一个高斯函数,则在傅里叶空间中它还是一个高斯函数,如下图所示:
维基百科中对连续可积函数
f
f
f的傅里叶变换给出的定义形式如下:
f
^
(
ξ
)
=
∫
−
∞
∞
f
(
x
)
e
−
2
π
i
x
ξ
d
x
,
ξ
为
定
义
在
频
域
上
的
任
意
实
数
\hat{f}(\xi)=\int _{-\infty}^{\infty}f(x)e^{-2 \pi ix\xi}dx, \xi为定义在频域上的任意实数
f^(ξ)=∫−∞∞f(x)e−2πixξdx,ξ为定义在频域上的任意实数
同时在适当的条件下,
f
^
\hat{f}
f^的逆傅里叶变换可得到
f
f
f:
f
(
x
)
=
∫
−
∞
∞
f
^
(
ξ
)
e
−
2
π
i
x
ξ
d
ξ
,
x
为
定
义
在
时
域
上
的
任
意
实
数
f(x)=\int _{-\infty}^{\infty}\hat{f}(\xi)e^{-2 \pi ix\xi}d\xi, x为定义在时域上的任意实数
f(x)=∫−∞∞f^(ξ)e−2πixξdξ,x为定义在时域上的任意实数
3.2 傅氏空间与离散傅里叶矩阵
傅里叶变换的奇妙之处就在于,将真实空间中复杂的波形通过“分解”之后可以得到若干简单的正弦波,这个“分解”操作是为傅里叶变换,从而“傅里叶空间”也可理解为“频率空间”,如下图所示:
离散傅里叶变换矩阵则是将离散傅里叶变换以矩阵乘法来表示的一种表达形式,其一般形式为:
F
=
1
n
[
1
1
.
.
.
1
1
1
w
.
.
.
w
n
−
2
w
n
−
1
1
w
2
.
.
.
w
2
(
n
−
2
)
w
2
(
n
−
1
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
w
n
−
1
.
.
.
w
(
n
−
1
)
(
n
−
2
)
w
(
n
−
1
)
2
]
F=\frac{1}{\sqrt{n}}\begin{bmatrix} 1&1&...&1&1\\ 1&\mathcal{w}&...&\mathcal{w}^{n-2}&\mathcal{w}^{n-1}\\ 1&\mathcal{w}^2&...&\mathcal{w}^{2(n-2)}&\mathcal{w}^{2(n-1)}\\ {...}&{...}&{...}&{...}&{...}&\\ \\ 1&\mathcal{w}^{n-1}&...&\mathcal{w}^{(n-1)(n-2)}&\mathcal{w}^{(n-1)^2}\end{bmatrix}
F=n1⎣⎢⎢⎢⎢⎢⎢⎡111...11ww2...wn−1...............1wn−2w2(n−2)...w(n−1)(n−2)1wn−1w2(n−1)...w(n−1)2⎦⎥⎥⎥⎥⎥⎥⎤
4.快速核相关计算
在part1中提及,实现快速相关计算的方法为:将模板、图像以及相应输出转换到傅里叶空间做点积运算。同时,KCF中创新性地使用了 循环转换模型(cyclic shift model),即前文提及的循环矩阵来解决了计算量的问题,将计算复杂度由 O ( n 2 ) \mathcal{O}(n^2) O(n2)降为了 O ( n l o n g n ) \mathcal{O}(nlong\mathcal {n}) O(nlongn)。
具体来说,由如下定理:循环矩阵都能够在傅氏空间中使用离散傅里叶矩阵进行对角化,即 X = F d i a g ( x ^ ) F H X = Fdiag(\hat{x})F^H X=Fdiag(x^)FH。
对于多项式 K ( X , X ′ ) = ( X T X ′ + a ) b \mathcal{K}(X,X')=(X^TX'+a)^b K(X,X′)=(XTX′+a)b,可有如下的表示形式: K X X ′ = ( F − 1 ( x ^ ∗ ⊙ x ′ ^ ) + a ) b \mathcal{K}^{XX'} = (\mathcal{F^{-1}}(\hat{x}^* \odot\hat{x'})+a)^b KXX′=(F−1(x^∗⊙x′^)+a)b,相关的证明过程参见原文,其中的 F − 1 \mathcal{F^{-1}} F−1代表离散傅里叶逆变换(IDFT), x ^ ∗ 与 x ′ ^ \hat{x}^* 与\hat{x'} x^∗与x′^代表各自在傅里叶空间中的映射。
径向基函数可以认为是
∣
∣
x
i
−
x
j
∣
∣
2
||x_i-x_j||^2
∣∣xi−xj∣∣2的函数,对于一些核函数h,径向基核如有如下的形式:
k
(
X
,
X
′
)
=
h
(
∣
∣
x
i
−
x
j
∣
∣
2
)
\mathcal{k}(X,X')=h(||x_i-x_j||^2)
k(X,X′)=h(∣∣xi−xj∣∣2)
于是在高斯核中,径向基函数的形式为:
K
x
x
′
=
e
x
p
(
−
1
σ
2
(
∣
∣
x
i
∣
∣
2
+
∣
∣
x
j
∣
∣
2
)
−
2
(
F
−
1
(
x
^
∗
⊙
x
′
^
)
)
T
)
K^{xx'}=exp(-\frac{1}{\sigma^2}(||x_i||^2+||x_j||^2)-2(\mathcal{F}^{-1}(\hat{x}^* \odot\hat{x'}))^T)
Kxx′=exp(−σ21(∣∣xi∣∣2+∣∣xj∣∣2)−2(F−1(x^∗⊙x′^))T),其中关于循环矩阵对角化及其推导的内容参见原文。这一部分计算的实现过程如下:
def kernel_correlation(self, x1, x2, sigma):
"""
核化的相关滤波操作
:param x1:
:param x2:
:param sigma:
:return:
"""
# 转换到傅里叶空间
fx1 = fft2(x1)
fx2 = fft2(x2)
# 相乘并返回共轭复数
tmp = conj(fx1) * fx2
# 离散傅里叶逆变换转换回真实空间
idft_rbf = ifft2(np.sum(tmp, axis=0))
# 将零频率分量移到频谱中心。
idft_rbf = fftshift(idft_rbf)
d = np.sum(x1 ** 2) + np.sum(x2 ** 2) - 2.0 * idft_rbf
# 径向基函数
k = np.exp(-1 / sigma ** 2 * np.abs(d) / d.size)
return k
5. 响应值的计算与分类器训练
训练的过程即是在核空间中做岭回归。具体来说,线性不可分的样本,经过非线性映射函数
ϕ
(
x
)
\phi (x)
ϕ(x)后可变为线性可分的样本,此时所处的新空间即时核空间,此时的任务是:在核空间中使用岭回归寻找一个分类器
f
(
x
i
)
=
w
T
ϕ
(
x
i
)
f(x_i)=\mathcal{w}^T \phi(x_i)
f(xi)=wTϕ(xi),目标在于寻找最优的
w
\mathcal{w}
w,根据梯度取零可以表示出
w
\mathcal{w}
w的向量表达式,详细推导过程参见原文。将
w
\mathcal{w}
w表示为如下形式后,可得到其对偶问题
w
=
∑
i
α
i
ϕ
(
x
i
)
\mathcal{w}=\sum_i\alpha_i\phi(x_i)
w=∑iαiϕ(xi),对偶表达为
α
=
m
i
n
α
∣
∣
ϕ
(
X
)
ϕ
(
X
)
T
α
−
y
∣
∣
2
+
λ
∣
∣
ϕ
(
X
)
T
α
∣
∣
\alpha = min_{\alpha}||\phi(X)\phi(X)^T\alpha-y||^2+\lambda||\phi(X)^T\alpha||
α=minα∣∣ϕ(X)ϕ(X)Tα−y∣∣2+λ∣∣ϕ(X)Tα∣∣
同样令其梯度为零可求得其表达式:
α
∗
=
(
ϕ
(
X
)
ϕ
(
x
)
T
+
λ
I
)
−
1
y
\alpha ^* = (\phi(X)\phi(x)^T+\lambda I)^{-1}y
α∗=(ϕ(X)ϕ(x)T+λI)−1y,由于并不清楚非线性映射函数
ϕ
(
X
)
\phi(X)
ϕ(X)的具体形式,并且只关心刻画在核空间的核矩阵
(
ϕ
(
X
)
ϕ
(
x
)
T
(\phi(X)\phi(x)^T
(ϕ(X)ϕ(x)T,故令
K
K
K表示这个核矩阵。
KCF算法始终未离开一个工具——循环矩阵,借助循环矩阵的傅里叶对角化来简化计算,核矩阵虽然得到了表示但是仍旧不知道其具体数值、形式,接下来的任务就变成了将 K K K对角化——希望找到一个核函数能使得对应的核矩阵是循环矩阵。原文中给出了如下的定理:
-
Given circulant data C (x), the corresponding kernel matrix K is circulant if the kernel function satisfifies
K ( x , x ′ ) = K ( M x , M x ′ ) K(x,x') = K(Mx, Mx') K(x,x′)=K(Mx,Mx′), for any permutation matrixM。
即:第一个样本和第二个样本都是由生成样本循环移位产生的,可以不是同一个样本。从而,在train函数中核矩阵的计算,以及 α \alpha α的计算方式有如下表示:
def train(self, x, y, sigma, lambdar):
"""
原文所给参考train函数
:param x:
:param y:
:param sigma:
:param lambdar:
:return:
"""
k = self.kernel_correlation(x, x, sigma)
return fft2(y) / (fft2(k) + lambdar)
在计算得到 α \alpha α之后,即可借助 α \alpha α来计算响应值:
def detect(self, x, z, sigma):
"""
原文所给参考detect函数
:param x:
:param z: x的HOG特征
:param sigma: 高斯参数
:return:
"""
k = self.kernel_correlation(x, z, sigma)
# 傅里叶逆变换的实部,对应响应的值
return np.real(ifft2(self.alphaf * fft2(k)))
之后即可根据响应值来更新检测的目标,详细代码参见update()函数。
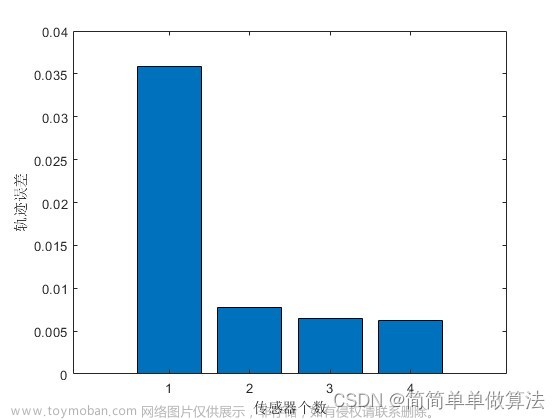
6. 运行结果
详见于result文件夹。文章来源:https://www.toymoban.com/news/detail-785546.html
Reference
- High-Speed Tracking with Kernelized Correlation Filters: https://arxiv.org/pdf/1404.7584
- Histogram of Oriented Gradients explained using OpenCV (learnopencv.com) : https://learnopencv.com/histogram-of-oriented-gradients/
- 傅里叶变换 - 维基百科:https://zh.wikipedia.org/wiki/傅里叶变换
- 从真实空间到傅立叶空间 - 知乎: https://zhuanlan.zhihu.com/p/37061414
- KCF目标跟踪方法分析与总结 - 一只有恒心的小菜鸟 - 博客园 : https://www.cnblogs.com/YiXiaoZhou/p/5925019.html
- GitHub代码仓库: https://github.com/chuanqi305/KCF
Appendix:库函数说明以及原文相关说明
1. HOG.py
| 项目1 | 对应内容 |
|---|---|
| 函数名 | cv2.HOGDescriptor.compute() |
| 功能描述 | 计算给定图像的HOG特征描述子 |
| 参数 |
img: 待计算的图像Patch winStride: 窗口滑动的步长 **padding **: Padding |
| 返回值 | 拼接好的n*1维HOG特征向量 |
2. KCF.py
| 项目1 | 对应内容 |
|---|---|
| 函数名 | numpy.conj() |
| 功能描述 | 帮助用户对任何复数进行共轭 |
| 参数 | x[array_like]: 输入值 |
| 返回值 | numpy.ndarray: x的复共轭 |
3. runKCF.py
| 项目1 | 对应内容 |
|---|---|
| 函数名 | cv2.VideoCapture(video_path or device index) |
| 功能描述 | 实例化一个VideoCapture对象 |
| 参数 | video_path:以.mp4/.avi结束的string类型 ,代表视频所在路径 or device index:指定camare的序号,值为0或-1 |
| 返回值 | VideoCapture对象 |
| 项目2 | 对应内容 |
|---|---|
| 函数名 | cv2.VideoCapture.read() |
| 功能描述 | 逐帧读取视频,返回值分两部分:是否正确读取以及每一帧的图像 |
| 参数 | 无 |
| 返回值 | bool ret:是否正确读取&&是否读取到视频末尾 np.ndarray frame:每一帧的图像,是一个三维矩阵 |
| 项目3 | 对应内容 |
|---|---|
| 函数名 | cv2.selectROI(windowName, img, showCrosshair=None, fromCenter=None) |
| 功能描述 | 在一幅图像中对特定图像区域以矩形框的形式进行截取 |
| 参数 |
windowName:选择的区域被显示在的窗口的名字 img:要在什么图片上选择ROI showCrosshair:是否在矩形框里画十字线. fromCenter:是否是从矩形框的中心开始画 |
| 返回值 | tuple (min_x, min_y, w, h),依次表示: 矩形框中最小的x值 矩形框中最小的y值 矩形框的宽 矩形框的高 |
| 项目4 | 对应内容 |
|---|---|
| 函数名 | cv2.rectangle(image, start_point, end_point, color, thickness) |
| 功能描述 | 在一幅图像上绘制一个矩形 |
| 参数 |
image:待绘制矩阵的图像 start_point:矩形的起始坐标,tuple类型 end_point:矩阵的结束坐标,tuple类型 color:绘制边框线的颜色 thickness:边框线的粗细 |
| 返回值 | np.ndarray:image |
| 项目5 | 对应内容 |
|---|---|
| 函数名 | cv2.VideoCapture.isOpen() |
| 功能描述 | 判断摄像头是否初始化成功 |
| 参数 | 无 |
| 返回值 | bool res:True or False |
| 项目6 | 对应内容 |
|---|---|
| 函数名 | argparse.ArgumentParser() |
| 功能描述 | 创建一个命令行参数解释器 |
| 参数 | 无(本例中) |
| 返回值 | 一个ArgumentParser对象 |
| 项目7 | 对应内容 |
|---|---|
| 函数名 | argparse.ArgumentParser.parse_args() |
| 功能描述 | 给ArgumentParser对象中的参数赋值 |
| 参数 | 无(本例中) |
| 返回值 | argparse.Namespace 参数名等 |
4. 原文参考源码与超参数
参考源码:文章来源地址https://www.toymoban.com/news/detail-785546.html
到了这里,关于单目标跟踪--KCF算法(核化相关滤波算法)Python实现(超详细)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!