Tarjan 算法——图论学习笔记-Toy模板网

这篇具有很好参考价值的文章主要介绍了Tarjan 算法——图论学习笔记。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

Tarjan 算法——图论学习笔记

Part.1 引入

在图论问题中，我们经常去研究一些连通性问题，比如：

有向图的联通性：传递闭包——Floyd 算法；
有向图连通性的对称性：强联通分量（SCC）——Tarjan 算法缩点；
无向图的联通性：并查集；
无向图的关键边：桥（割边）、边双——Tarjan 算法缩点；
无向图的关键点：割点、点双——Tarjan 建立圆方树。

那么，Tarjan 算法到底是什么呢？

Part.2 Tarjan 算法求 SCC

SCC，即强联通分量，是一张有向图的极大子图，满足任意两个点 $u, v$ 强联通（即 $u$ 可以到 $v$ ， $v$ 可以到 $u$ ）。一个重要的性质就是强联通具有传递性。

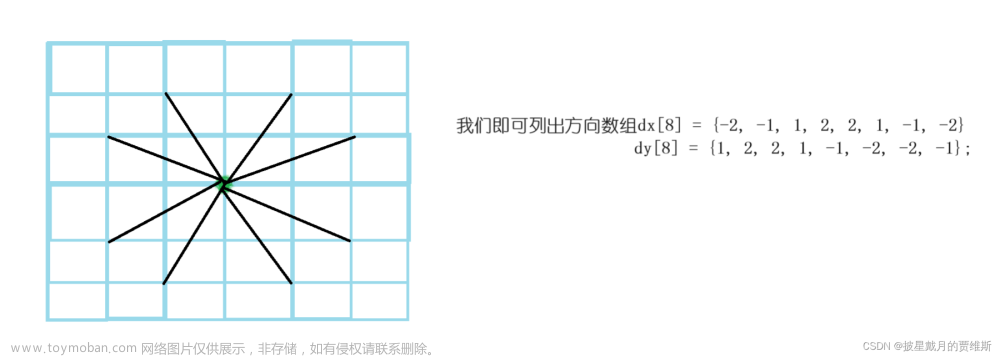
在有向图中，我们会用 Tarjan 算法去建一棵 DFS 生成树：

Tarjan 算法——图论学习笔记,学习笔记,算法,图论,图搜索算法

在 DFS 的过程中，我们会对于每个点，处理出一个 DFS 序号，并把 DFS 到的点放入一个栈中，定义一个新数组 $l o w$ ，其中， $low_x$ 表示 $x$ 号节点能跳到的在栈中的 DFS 序的最小值。

接下来就是 Tarjan 算法的核心思想：对于一个点 $u$ ，如果满足 $dfn_u=low_u$ ，说明点 $u$ 不存在向上跳的非树边，是一个顶点。那么当前节点及以后在栈中的节点就构成了一个 SCC。

代码如下：

int dfn[N],low[N],idx,stk[N],top,scc[N],c;
bool inc[N];
void dfs(int u)
{
	dfn[u] = low[u] = ++idx,stk[++top] = u,inc[u] = 1;
	for(int i = head[u];i;i = nxt[i])//建 DFS 树且维护 low 数组
	{
		int v = to[i];
		if(!dfn[v])//树边
		{
			dfs(v);
			low[u] = min(low[u],low[v]);
		}
		else if(inc[v]) low[u] = min(low[u],dfn[v]);//非树边
	}
	if(dfn[u]==low[u])//是一个顶点，构成一个 SCC
	{
		c++;//SCC个数+1
		while(stk[top]!=u)
			inc[stk[top]] = 0,scc[stk[top]] = c,top--;
		inc[u] = 0,scc[u] = c,top--;
	}
}

求 SCC 有什么用呢？

在一些与连通性有关的问题中，我们把每个 SCC 缩成一个点，可以得到一个 DAG，因为如果还环的话就能形成一个新的 SCC。这样就可以在 DAG 上做 DP 之类来解决问题；
在 2-SAT 问题（有 $m$ 个二元方程，并且每个未知数都是 $0$ 或 $1$ ）中，我们求解和判无解也需要用到 SCC，有兴趣的可以自己去看。

Part.3 Tarjan 求割边、边双

在无向图中，定义割边（也叫桥）为删掉这条边后图的连通性改变的边。边双连通分量（简称边双），即为不存在割边的极大子图，与 SCC 一样，具有传递性。

和求 SCC 一样，我们还是去建立一颗 DFS 树。我们重新定义 $low_x$ 为 $x$ 号节点最多通过一条非树边能跳到的 DFS 序的最小值。那一条连接 $u, v$ 的边是桥当且仅当 $dfn_u<low_v$ ，就相当于 $v$ 经过一条非树边到不了 $u$ ，这样肯定是割边。

至于求边双，就是每次选一个点，在不经过桥的前提下能到的所有点就形成了一个边双。

一个细节就是边表的 cnt 记得赋值为 $1$ ，方便求反向边。

代码和求 SCC 差不多，具体如下：

int n,m,dfn[N],low[N],t;
bool brg[M];
void dfs(int u,int ine)//求割边
{
	dfn[u] = low[u] = ++t;
	for(int i = head[u];i;i = nxt[i])
	{
		if(i==ine) continue;//不往回走
		int v = to[i];
		if(dfn[v]==0)
		{
			dfs(v,i^1);
			low[u] = min(low[u],low[v]);
			if(low[v]>dfn[u]) brg[i] = brg[i^1] = 1;//是割边
		}
		else low[u] = min(low[u],dfn[v]);
	}
}
bool vis[N];
int c;//记录边双的个数
void dfs(int u)
{
	ans[c].push_back(u),vis[u] = 1;
	for(int i = head[u];i;i = nxt[i])
	{
		if(brg[i]) continue;//不经过桥
		int v = to[i];
		if(!vis[v]) dfs(v);
	}
}

Part.4 Tarjan 求割点、点双

参照割边、边双的定义，割点为删掉这个点后图的连通性改变的点。点双连通分量（简称点双），即为不存在割点的极大子图。但是点双不具有传递性，所以点双是最难的。画一个图就知道了：

Tarjan 算法——图论学习笔记,学习笔记,算法,图论,图搜索算法

左边 $4$ 个点是个点双，右边 $4$ 个点也是点双，但是整张图却不是点双，因为中间的点是个割点。

仍然建出 DFS 树，发现用顶点找出一个点双已经不可行了，因为一个点能在多个点双当中。

Tarjan 算法——图论学习笔记,学习笔记,算法,图论,图搜索算法

我们发现，两个点双至多有一个交点，这个点就是割点。如上图，这个交点一定在下面的点双中 $df n$ 是最小的，而上面的点双可以由另外的点（类似树根）求出。

所以，对于一条边 $(u, v)$ ，如果满足 $low_v\ge dfn_u$ ，就说明找到一个点双了。

上代码：

int n,m,dfn[N],low[N],c,stk[N],top,t;
vector<int> ans[N];
void dfs(int u,int fa)
{
	dfn[u] = low[u] = ++t;
	stk[++top] = u;
	int son = 0;
	for(int i = head[u];i;i = nxt[i])
	{
		int v = to[i];
		if(v==fa) continue;
		if(dfn[v]==0)
		{
			++son;
			dfs(v,u);
			low[u] = min(low[u],low[v]);
			if(low[v]>=dfn[u])//找到点双
			{
				++c;
				while(stk[top]!=v) ans[c].push_back(stk[top--]);
				ans[c].push_back(v);--top;ans[c].push_back(u);//细节：不能将点 u 弹出栈
			}
		}
		else low[u] = min(low[u],dfn[v]);
	}
	if(fa==0&&son==0) ans[++c].push_back(u);//特判：单独一个点也是点双
}