Android Matrix （三）矩阵组合和应用变换-Toy模板网

这篇具有很好参考价值的文章主要介绍了Android Matrix （三）矩阵组合和应用变换。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在 Android 开发中，Matrix 类不仅提供了 mapPoints 方法来变换点坐标，还提供了多种其他用法，使其成为处理图像和视图变换的强大工具。以下是 Matrix 类的一些关键用法：
Android Matrix （三）矩阵组合和应用变换,android,矩阵,线性代数,android

1. 变换方法

setTranslate(float dx, float dy): 设置矩阵为平移矩阵。
setScale(float sx, float sy, float px, float py): 设置矩阵为缩放矩阵，px 和 py 为缩放的轴心。
setRotate(float degrees, float px, float py): 设置矩阵为旋转矩阵，degrees 为旋转角度，px 和 py 为旋转的轴心。
setSkew(float kx, float ky, float px, float py): 设置矩阵为倾斜矩阵，kx 和 ky 为倾斜角度，px 和 py 为倾斜的轴心。

2. 组合和应用变换

postConcat(Matrix other): 后置连接另一个矩阵，可以用于组合多个变换。
preConcat(Matrix other): 前置连接另一个矩阵，同样用于组合变换，但顺序与 postConcat 相反。
setConcat(Matrix a, Matrix b): 将两个矩阵的变换组合起来。

3. 变换应用

mapRect(RectF rect): 变换矩形区域。
mapVectors(float[] vecs): 变换向量而不涉及位移。
mapRadius(float radius): 变换圆的半径，常用于变换圆形或椭圆。

4. 矩阵操作

reset(): 重置矩阵为单位矩阵。
set(Matrix src): 设置当前矩阵与指定矩阵相同。
invert(Matrix inverse): 计算当前矩阵的逆矩阵。

5. 辅助方法

isIdentity(): 检查矩阵是否为单位矩阵。
rectStaysRect(): 检查矩阵变换后，矩形是否仍然保持为矩形。

6. 与 Canvas 的结合

Matrix 类在结合 Canvas 使用时尤为强大，可用于实现图像、文本和形状的复杂变换效果。

canvas.setMatrix(Matrix matrix): 设置画布的变换矩阵。
canvas.concat(Matrix matrix): 将画布当前的变换矩阵与另一个矩阵组合。

这些方法使得 Matrix 成为一个多功能且强大的工具，可以在图形处理、动画制作和视图变换中发挥关键作用。通过这些方法的组合使用，开发者可以实现复杂和精确的图形变换效果。接下来将对第2部分重点介绍一下。
Android Matrix （三）矩阵组合和应用变换,android,矩阵,线性代数,android

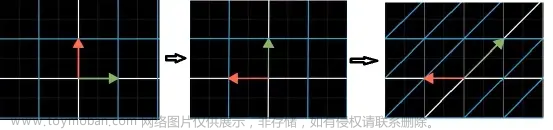
在 Android 的 Matrix 类中，组合变换是一项非常强大的功能。postConcat、preConcat 和 setConcat 方法允许开发者以灵活的方式组合不同的图形变换。以下是这些方法的详细说明和例子：

1. postConcat(Matrix other)

postConcat 方法将当前矩阵与另一个矩阵相乘，乘法顺序是先应用当前矩阵的变换，然后应用参数中提供的矩阵的变换。

例子

假设您想先旋转一个图像，然后再对其进行缩放：

val matrix = Matrix()
matrix.setRotate(45f) // 旋转45度

val scaleMatrix = Matrix()
scaleMatrix.setScale(2f, 2f) // 缩放，x和y都放大两倍

matrix.postConcat(scaleMatrix) // 先旋转，再缩放

2. preConcat(Matrix other)

与 postConcat 相反，preConcat 方法先应用参数中的矩阵变换，然后应用当前矩阵的变换。

例子

假设您想先缩放一个图像，然后再旋转它：

val matrix = Matrix()
matrix.setRotate(45f) // 旋转45度

val scaleMatrix = Matrix()
scaleMatrix.setScale(2f, 2f) // 缩放，x和y都放大两倍

matrix.preConcat(scaleMatrix) // 先缩放，再旋转

3. setConcat(Matrix a, Matrix b)

setConcat 方法结合两个矩阵的变换，先应用第二个参数 b 的变换，然后是第一个参数 a 的变换。

例子

假设您有两个矩阵，一个用于旋转，另一个用于缩放，您想先缩放后旋转：文章来源地址https://www.toymoban.com/news/detail-786201.html

val rotateMatrix = Matrix()
rotateMatrix.setRotate(45f) // 旋转45度

val scaleMatrix = Matrix()
scaleMatrix.setScale(2f, 2f) // 缩放，x和y都放大两倍

val resultMatrix = Matrix()
resultMatrix.setConcat(rotateMatrix, scaleMatrix) // 先缩放，再旋转