1. Toy模板网首页
  2. > Toy博客

【C数据结构】迷宫问题

9月前 作者：Ahao_te 分类：Toy博客 阅读(38) 违法举报

这篇具有很好参考价值的文章主要介绍了【C数据结构】迷宫问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

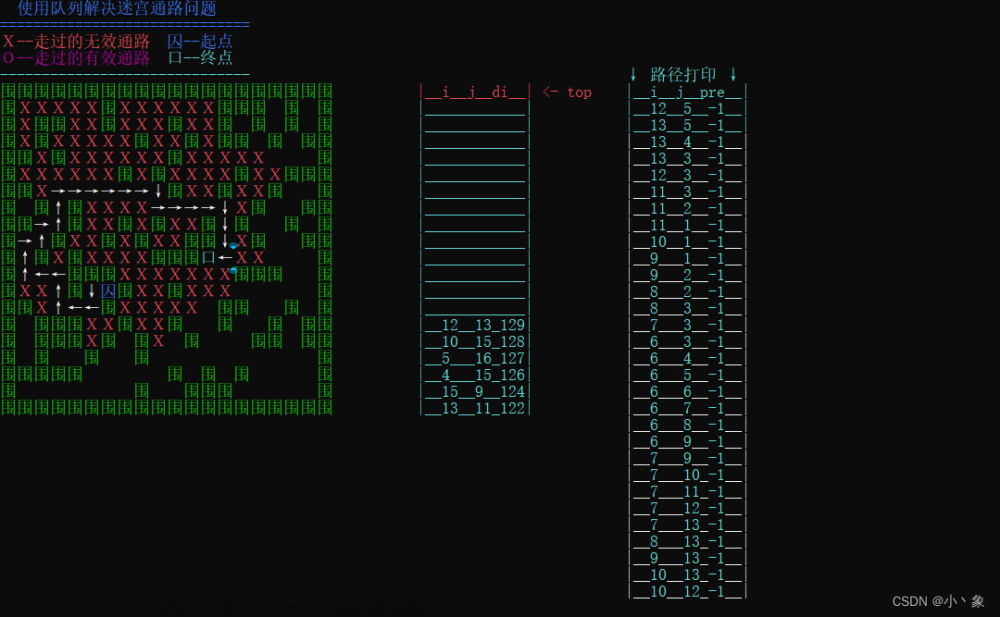
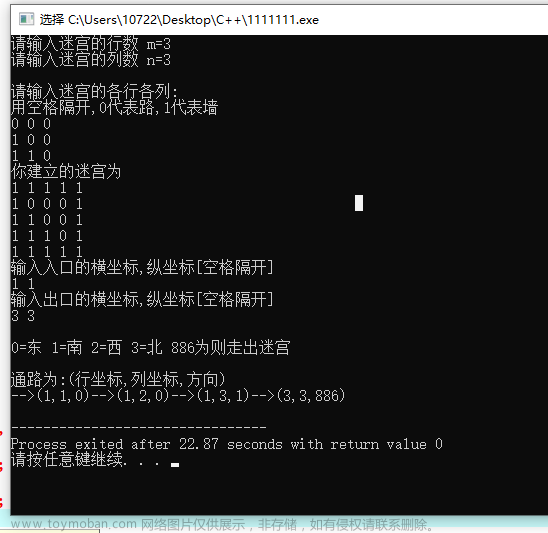
前言:本章记录作者学习中，遇到的两个比较有趣的问题，一个简单和一个较复杂的迷宫问题。

 
 

一、迷宫问题的思路

让我们先来看简单的：迷宫问题
它的具体要求：

输入描述：
输入两个整数，分别表示二维数组的行数，列数。再输入相应的数组，其中的1表示墙壁，0表示可以走的路。数据保证有唯一解,不考虑有多解的情况，即迷宫只有一条通道。
如

5 5
0 1 0 0 0
0 1 1 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

要求输出 如：

(0,0)
(1,0)
(2,0)
(2,1)
(2,2)
(2,3)
(2,4)
(3,4)
(4,4)

这道题的重点有：只能上下左右走，不能斜着走；左上角为起点，右下角为终点；只有唯一解。

思路分析：

  1. 对于不支持变长数组的C版本来说，如果需要实现二维变长数组的话，就需要动态开辟二维数组。
  2. 每次需要对上下左右四个方向进行判断，才能到达下一个坐标，并且如果四个方向都不能走而且还没到达终点，那么就要往回走。
  3. 为了判断往回是否还有其它能走的方向，我们需要对走过的坐标进行标记，这样就不会出现走重复的路线。
  4. 在结束的时候，我们需要打印这条路径的每个坐标，那么我们就需要对我们走过的坐标进行储存，对到达不了终点的路上的坐标消除，所以似乎需要栈来帮我们储存这个坐标。

 
 

二、简单迷宫的代码实现

动态实现二维变长数组：

先创建一个二维指针，储存N个一维指针的地址，这些一维指针都分别指向一个开辟了M个数据的数组
迷宫问题,数据结构,c语言,数据结构,开发语言

#include<stdio.h>
void PrintMaze(int** maze, int N, int M)
{
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < M; j++)
		{
			printf("%d ", maze[i][j]);
		}
		printf("\n");
	}
}

int main()
{
	int N = 0, M = 0;
	scanf("%d %d", &N, &M);

	//动态开辟二维数组
	int** maze = (int**)malloc(sizeof(int*) * N);
	for (int i = 0; i < N; i++)
	{
		maze[i] = (int*)malloc(sizeof(int) * M);
	}
	
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < M; j++)
		{
			scanf("%d", &maze[i][j]);
		}
	}

	PrintMaze(maze, N, M);//测试是否能打印，看看有没有问题
	
	for (int i = 0; i < N; i++)
	{
		free(maze[i]);
	}
	free(maze);
	return 0;
}

 
 
四个方向判断的实现：
为了方便操作，我们建立一个结构体类型，方便定义坐标。

typedef struct position
{
	int row;
	int col;
}PT;

并且在测试页定义初始变量：

PT cur = { 0,0 };
  1. 从（0，0）坐标开始，假设先判断上下，再判断左右，如果能通过就移动坐标，并且进入下次判断，直到到达终点，或者不能移动，并且需要对每次到达的坐标进行标记，假设标记为2.
  2. 如果四个方向都不能走，并且没到达终点，那么将一直返回上一个位置，直到有其它方向能走。
  3. 如果到达终点，返回true，直到跳出所有递归。
//判断下一个坐标是否能通过
bool IsPass(int** maze, int N, int M, PT cur)
{
	if (cur.col >= 0 && cur.col < M && cur.row >= 0 && cur.row < N
		&& maze[cur.row][cur.col] == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

bool GetPath(int** maze, int N, int M, PT cur)
{
	//到达终点
	if (cur.row == N - 1 && cur.col == M - 1)
	{
		return true;
	}


	//上下左右判断
	PT next;
	maze[cur.row][cur.col] = 2;//标记

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, N, M, next))
	{	
		//上方向可以通过就移动到上方向的坐标，并且继续判断四个方向是否可以移动
		if (GetPath(maze, N, M, next))
		{
			//1.只有到达终点才会进入这次判断，并且一直返回true，直到退出所有递归。
			//2.因为这题只有唯一解，所以一旦找到终点就可以直接返回。
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}
	
	//四个方向都不能走，就返回false，跳到上一个坐标判断它剩下的其它方向是否可以走
	return false;
}

 
 
利用栈记录坐标的实现：
因为C语言没有自己的栈，所以我们还需要自己搭建一个栈。
栈的实现

  1. 每次判断坐标前，先将当前坐标存入栈中，如果四个方向都不能走的时候，再出栈。
  2. 当到达终点，返回完后，对栈中数据进行处理。
  3. 因为栈中数据打印后与题目要求的打印相反，所有需要再创建一个栈，将当前栈中的数据导入另一个栈中，从而实现相反的打印。

完整代码：

#include<stdio.h>;
#include<stdlib.h>;
#include<assert.h>;
#include<stdbool.h>;

typedef struct position
{
	int row;
	int col;
}PT;

typedef PT STDataType;
typedef struct stack {
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST*ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

//

void StackInit(ST* ps) {
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;//或者-1
	
}

void StackPush(ST* ps, STDataType x) {

	if (ps->capacity == ps->top) {
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL) {
			printf("realloc fail\n");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top++] = x;
}

void StackDestroy(ST* ps) {
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

void StackPop(ST* ps) {
	assert(ps);
	/*assert(ps->top > 0);*/
	assert(!StackEmpty(ps));
	ps->top--;
}

STDataType StackTop(ST* ps) {
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top-1];
}

int StackSize(ST* ps) {
	assert(ps);
	return ps->top;
}

bool StackEmpty(ST* ps) {
	return ps->top==0;
}

//

ST path;//可以创局部变量，这里方便一下

bool IsPass(int** maze, int N, int M, PT cur)
{
	if (cur.col >= 0 && cur.col < M && cur.row >= 0 && cur.row < N
		&& maze[cur.row][cur.col] == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

bool GetPath(int** maze, int N, int M, PT cur)
{
	//走过的坐标先入栈
	StackPush(&path, cur);

	//到达终点
	if (cur.row == N - 1 && cur.col == M - 1)
	{
		return true;
	}


	//上下左右判断
	PT next;
	maze[cur.row][cur.col] = 2;

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next))
		{
			return true;
		}
	}

	//四个方向都不能走，就出栈返回
	StackPop(&path);
	return false;
}

void PrintPath(ST* ps)
{
	ST rpath;//创建需要导数据的另一个栈
	StackInit(&rpath);

	while (!StackEmpty(ps))
	{
		StackPush(&rpath, StackTop(ps));
		StackPop(ps);
	}

	while (!StackEmpty(&rpath))
	{
		PT cur = StackTop(&rpath);
		printf("(%d,%d)\n", cur.row, cur.col);
		StackPop(&rpath);
	}

	StackDestroy(&rpath);
}

int main()
{
	int N = 0, M = 0;
	scanf("%d %d", &N, &M);

	PT cur = { 0,0 };

	StackInit(&path);
	//动态开辟二维数组
	int** maze = (int**)malloc(sizeof(int*) * N);
	for (int i = 0; i < N; i++)
	{
		maze[i] = (int*)malloc(sizeof(int) * M);
	}

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < M; j++)
		{
			scanf("%d", &maze[i][j]);
		}
	}

	if (GetPath(maze, N, M, cur))
	{
		PrintPath(&path);
	}

	StackDestroy(&path);

	for (int i = 0; i < N; i++)
	{
		free(maze[i]);
	}
	free(maze);
	return 0;
}

三、地下迷宫问题的思路

看看这个问题：地下迷宫
迷宫问题,数据结构,c语言,数据结构,开发语言
迷宫问题,数据结构,c语言,数据结构,开发语言

记录重点：

  1. 现在0代表障碍物，1代表通路，并且增加了体力值，左右移动减1，上移动减3，下移动不消耗，如果体力值为0还未到达出口，将无法逃离迷宫。
  2. （0，0）位置为起点，（0，m-1）位置为出口，并且现在要求最后打印的是最短路径。
  3. 体力值为0还未到达出口，结果需要打印：Can not escape!
  4. 坐标打印改变变成[0,0],

分析思路：

  1. 增加体力值P变量，并且当判断四个方向分别可以通过时，同时传入参数P，向上方向能通过传参数P-3，向左或者右方向能通过传P-1，向下传P；同时改变通路为1，出口为（0，m-1）
  2. 为了找到最短路径，直接通过建两个栈，一个记录当前路径的坐标，一个记录当前为止最短路径的坐标；利用递归列出所有可以走的路径，然后挑出最小的路径。（下面会重点介绍如何安全的转移栈以及如何用递归找到所有路径）
  3. 挑选的路径也要满足体力值条件；当所有的路径，体力都会耗尽且没有到达终点，记录最短路径坐标的栈为空，就可以通过这个情况打印Can not escape!。

四、地下迷宫的代码实现

先搭建一个基本的框架。

  1. 动态创建二维数组
  2. 获得路径
  3. 打印路径

创建体力值，并且改变通路条件、出口、打印和函数参数调用

//

ST path;//可以创局部变量，这里方便一下

bool IsPass(int** maze, int N, int M, PT cur)
{
	if (cur.col >= 0 && cur.col < M && cur.row >= 0 && cur.row < N
		&& maze[cur.row][cur.col] == 1) //通路条件为1
	{
		return true;
	}
	else
	{
		return false;
	}
}

bool GetPath(int** maze, int N, int M, PT cur, int P)
{
	//走过的坐标先入栈
	StackPush(&path, cur);

	//到达终点
	if (cur.row == 0 && cur.col == M - 1) //终点为(0,m-1)
	{
		return true;
	}


	//上下左右判断
	PT next;
	maze[cur.row][cur.col] = 2;

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next, P-3))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next, P))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next, P-1))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, N, M, next))
	{
		if (GetPath(maze, N, M, next, P-1))
		{
			return true;
		}
	}

	//四个方向都不能走，就出栈返回
	StackPop(&path);
	return false;
}

void PrintPath(ST* ps)
{
	ST rpath;
	StackInit(&rpath);

	while (!StackEmpty(ps))
	{
		StackPush(&rpath, StackTop(ps));
		StackPop(ps);
	}

	while (StackSize(&rpath) > 1)
	{
		PT cur = StackTop(&rpath);
		printf("[%d,%d],", cur.row, cur.col);
		StackPop(&rpath);
	}
	//前面打印带"," 最后一个不带
	PT cur = StackTop(&rpath);
	printf("[%d,%d]\n", cur.row, cur.col);
	StackPop(&rpath);

	StackDestroy(&rpath);
}

int main()
{
	int N = 0, M = 0, P = 0; //体力值P
	scanf("%d %d %d", &N, &M, &P);

	PT cur = { 0,0 };

	StackInit(&path);
	//动态开辟二维数组
	int** maze = (int**)malloc(sizeof(int*) * N);
	for (int i = 0; i < N; i++)
	{
		maze[i] = (int*)malloc(sizeof(int) * M);
	}

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < M; j++)
		{
			scanf("%d", &maze[i][j]);
		}
	}

	if (GetPath(maze, N, M, cur, P))
	{
		PrintPath(&path);
	}

	StackDestroy(&path);

	for (int i = 0; i < N; i++)
	{
		free(maze[i]);
	}
	free(maze);
	return 0;
}

找到所有的路径和记录的实现：
主要难的是这里的递归思想。

  1. 如果有通路，就移动到下一个坐标进行四个方向的判断，直到体力值用完到达终点或者没有到达终点。
  2. 到达终点之后，第一次到达终点保存这条路径，之后比较两条路径，选最短的路径；之后回到上一个坐标点
  3. 到达终点之后，当前坐标继续进行四个方向的判断，当四个方向都不能通过的时候，为了让下次能访问这个坐标，将这个坐标恢复为1，并且返回上一个坐标。
  4. 每个可以通过的坐标都将进行4个方向的判断，当所有可通过坐标判断完成，递归函数结束。

为什么要创建两个栈？
因为有一个栈里面的数据是会变的，所有需要深拷贝一个栈记录原来不变的数据。


void StackCopy(ST* path, ST* minpath)
{

	minpath->a = (STDataType*)malloc(sizeof(STDataType*) * path->capacity);
	memcpy(minpath->a, path->a, sizeof(STDataType) * path->top);
	minpath->capacity = path->capacity;
	minpath->top = path->top;
}


void GetPath(int** maze, int N, int M, PT cur, int P)
{
	StackPush(&path, cur);


	//到达终点
	if (cur.row == 0 && cur.col == M - 1)
	{
		if (P >= 0 && StackEmpty(&minpath) || StackSize(&path) < StackSize(&minpath))
		{
			StackDestroy(&minpath);
			StackCopy(&path, &minpath);
		}
	}


	//上下左右判断
	PT next;
	maze[cur.row][cur.col] = 2;

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P - 3);
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P);
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P - 1);
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P - 1);
	}

	//恢复
	maze[cur.row][cur.col] = 1;
	StackPop(&path);
}

完整代码：

#include<stdio.h>;
#include<stdlib.h>;
#include<assert.h>;
#include<stdbool.h>;
#include<string.h>;

typedef struct position
{
	int row;
	int col;
}PT;

typedef PT STDataType;
typedef struct stack {
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST* ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);



void StackInit(ST* ps) {
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;//或者-1

}

void StackPush(ST* ps, STDataType x) {

	if (ps->capacity == ps->top) {
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL) {
			printf("realloc fail\n");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top++] = x;
}

void StackDestroy(ST* ps) {
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

void StackPop(ST* ps)
{
	assert(ps);
	/*assert(ps->top > 0);*/
	assert(!StackEmpty(ps));
	ps->top--;
}

STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];
}

int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

bool StackEmpty(ST* ps)
{
	return ps->top == 0;
}

void StackCopy(ST* path, ST* minpath)
{

	minpath->a = (STDataType*)malloc(sizeof(STDataType*) * path->capacity);
	memcpy(minpath->a, path->a, sizeof(STDataType) * path->top);
	minpath->capacity = path->capacity;
	minpath->top = path->top;
}


ST path;
ST minpath;

//判断通路
bool IsPass(int** maze, int N, int M, PT cur)
{
	if (cur.col >= 0 && cur.col < M && cur.row >= 0 && cur.row < N
		&& maze[cur.row][cur.col] == 1)
	{
		return true;
	}
	else
	{
		return false;
	}
}

//递归找到最小路径
void GetPath(int** maze, int N, int M, PT cur, int P)
{
	StackPush(&path, cur);


	//到达终点
	if (cur.row == 0 && cur.col == M - 1)
	{
		if (P >= 0 && StackEmpty(&minpath) || StackSize(&path) < StackSize(&minpath))
		{
			StackDestroy(&minpath);
			StackCopy(&path, &minpath);
		}
	}


	//上下左右判断
	PT next;
	maze[cur.row][cur.col] = 2;

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P - 3);
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P);
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P - 1);
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, N, M, next))
	{
		GetPath(maze, N, M, next, P - 1);
	}

	maze[cur.row][cur.col] = 1;
	StackPop(&path);
}

//打印坐标
void PrintPath(ST* ps)
{
	ST rpath;
	StackInit(&rpath);

	while (!StackEmpty(ps))
	{
		StackPush(&rpath, StackTop(ps));
		StackPop(ps);
	}

	while (StackSize(&rpath) > 1)
	{
		PT cur = StackTop(&rpath);
		printf("[%d,%d],", cur.row, cur.col);
		StackPop(&rpath);
	}
	PT cur = StackTop(&rpath);
	printf("[%d,%d]\n", cur.row, cur.col);
	StackPop(&rpath);

	StackDestroy(&rpath);
}

int main()
{
	int N = 0, M = 0, P = 0;
	scanf("%d %d %d", &N, &M, &P);

	PT cur = { 0,0 };

	StackInit(&path);
	StackInit(&minpath);
	//动态开辟二维数组
	int** maze = (int**)malloc(sizeof(int*) * N);
	for (int i = 0; i < N; i++)
	{
		maze[i] = (int*)malloc(sizeof(int) * M);
	}

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < M; j++)
		{
			scanf("%d", &maze[i][j]);
		}
	}

	//获得最小路径
	GetPath(maze, N, M, cur, P);
	
	if (!StackEmpty(&minpath))
	{
		PrintPath(&minpath);
	}
	else
	{
		printf("Can not escape!");
	}

	StackDestroy(&path);
	StackDestroy(&minpath);

	for (int i = 0; i < N; i++)
	{
		free(maze[i]);
	}
	free(maze);
	return 0;
}

总结：迷宫问题的难点主要是怎么找到路径，如何打印路径坐标。如果能解决这些问题，那么对递归的理解以及栈的应用有很大的提升。文章来源地址https://www.toymoban.com/news/detail-786314.html

到了这里，关于【C数据结构】迷宫问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 【数据结构】迷宫问题实现(包含界面)

    【数据结构】迷宫问题实现(包含界面)

    🎈🎈 问题描述：假设迷宫由m行n列构成，有一个入口和一个出口，入口坐标为(1,1),出口坐标为(m,n),试设计并验证一下算法：找出一条入口通往出口的路径，或报告一个\\\"无法通过\\\"的信息。 具体需求如下： 用C语言实现顺序存储结构上队列的基本操作，然后利用该队列的基本操

    2024年02月04日
    浏览(36)
  • 数据结构——迷宫问题（顺序栈、C++）

    数据结构——迷宫问题（顺序栈、C++）

     讲解： 一、采用二维数组和srand函数随机生成只有0和1的迷宫。 二、求解迷宫大概思路：先将入口处的坐标即方向d入栈，然后当栈不为空时，取出栈顶（即当前节点）的数据。遍历当前节点的四个方向，找到可行的下一个节点，并将其入栈；如没有可行的下一个节点，则将

    2024年02月13日
    浏览(33)
  • 《数据结构与算法分析》课程设计——迷宫问题

    《数据结构与算法分析》课程设计——迷宫问题

    中国矿业大学信控学院   补一下我之前在博客园发布的内容  懒得调了， 想复制完整代码直接复制最下面的 ，想复制分布代码去看我博客园链接吧 《数据结构与算法分析》课程设计——迷宫问题 - 刷子zz - 博客园 一、  问题描述 问题中迷宫可用方阵[m,n]表示，0表示能通过

    2024年02月10日
    浏览(49)
  • C数据结构与算法——队列 应用（C语言纯享版 迷宫）

    C数据结构与算法——队列 应用（C语言纯享版 迷宫）

    实验任务 (1) 掌握顺序循环队列及其C语言的表示； (2) 掌握入队、出队等基本算法的实现； (3) 掌握顺序循环队列的基本应用（求解迷宫通路）。 实验内容 使用C语言实现顺序循环队列的类型定义与算法函数； 编写main()函数并根据需要修改、补充相关的类型定义与函数，以实

    2024年02月15日
    浏览(52)
  • 数据结构与算法大作业：走迷宫程序（C语言,DFS)(代码以及思路）

    数据结构与算法大作业：走迷宫程序（C语言,DFS)(代码以及思路）

    好家伙，写大作业,本篇为代码的思路讲解   问题描述： 以一个 m * n 的长方阵表示迷宫， 0和1分别表示迷宫的通路和障碍。 设计一个程序， 对任意设定的迷宫， 求出一条从入口到出口的通路， 或得出没有通路的结论。 基本要求： （1） 实现一个以链表做存储的栈类型，

    2024年02月03日
    浏览(40)
  • 数据结构--迷宫求解

    数据结构--迷宫求解

    文章目录 一、问题的描述 二、系统功能设计 三、各个代码部分 四、整体代码及其运行 五、总结 迷宫求解--C语言 在一个迷宫中，需要我们找到出去的道路，并且得到的路经是最短的。 迷宫设置如下：迷宫使用标记（0，1，2，3分别代表迷宫的墙壁，通道，入口和出口） 从开

    2024年02月15日
    浏览(38)
  • 数据结构线性结构（二）6迷宫最短路径

    数据结构线性结构（二）6迷宫最短路径

       

    2024年02月08日
    浏览(31)
  • 数据结构—约瑟夫环问题(C语言版)

    数据结构—约瑟夫环问题(C语言版)

    目录 首先什么是约瑟夫环 约瑟夫环实现方式 一、创建结构体变量 二、初始化链表 三、构建循环链表 四、删除链表  五、完整代码及注释讲解 约瑟夫环 是 循环链表 中的一个经典问题；题目描述：n 个人围成一圈，从第一个人开始报数,数到 m 的人出列，再由下一个人重新

    2024年02月11日
    浏览(41)
  • 软件开发中常用数据结构介绍：C语言队列

    软件开发中常用数据结构介绍：C语言队列

    工作之余来写写C语言相关知识，以免忘记。今天就来聊聊 C语言实现循环队列 ，我是分享人M哥，目前从事车载控制器的软件开发及测试工作。 学习过程中如有任何疑问，可底下评论！ 如果觉得文章内容在工作学习中有帮助到你，麻烦 点赞收藏评论+关注 走一波！感谢各位的

    2024年02月11日
    浏览(46)
  • 《数据结构、算法与应用C++语言描述》-列车车厢重排问题

    《数据结构、算法与应用C++语言描述》-列车车厢重排问题

    完整可编译运行代码见：Github::Data-Structures-Algorithms-and-Applications/_10Train_carriages_rearrangement/ 一列货运列车有 n 节车厢，每节车厢要停靠在不同的车站。假设 n个车站从 1 到n 编号，而且货运列车按照从n到1的顺序经过车站。车厢的编号与它们要停靠的车站编号相同。为了便于从

    2024年04月10日
    浏览(61)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包