三维旋转矩阵描述的是在三维空间中物体的旋转关系,我们难以直观地从旋转矩阵上看出旋转的具体情况。但是,它可以由欧拉角变换而来,也就是可以视为绕着xyz三个轴分别进行旋转后结果的叠加,是一系列三角函数相乘的结果。比如,通常我们所使用的rpy角:

关于不同旋转表达方式之间的转换这里不做赘述,感兴趣的可以参考:四种三维空间旋转表示方法“轴角、旋转矩阵、欧拉角、四元数”之间的相互转换总结。下面直接进入正题,理解旋转矩阵中不同元素的含义。
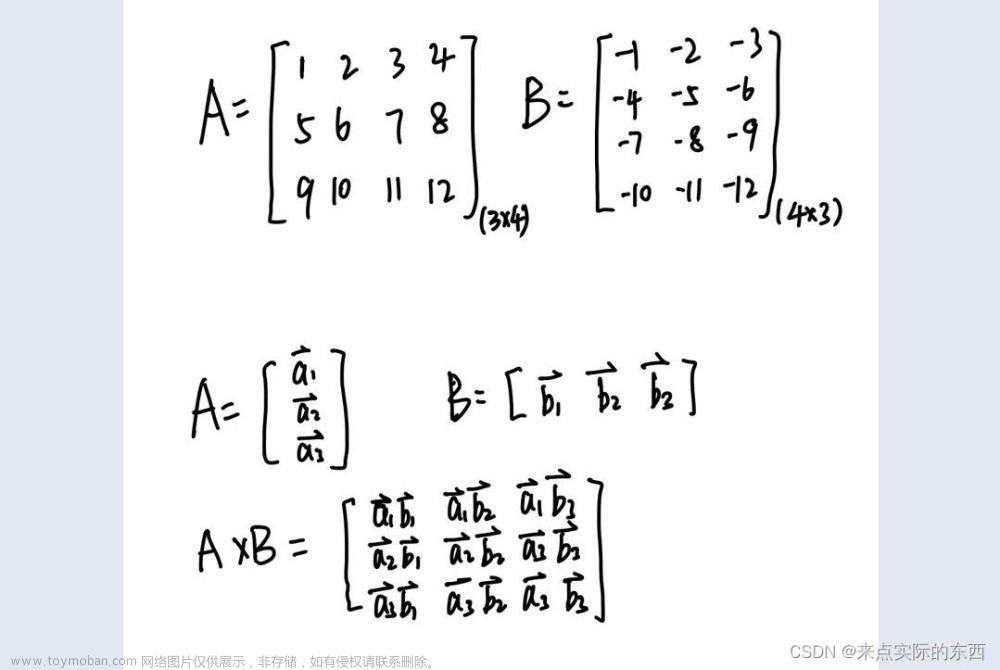
记被旋转的点p1坐标为(x1, y1, z1),经过旋转矩阵R3×3的作用后,其在新坐标系下的坐标p2变为(x2, y2, z2)。用代码语言描述如下:
# 定义
p1 = [x1,y1,z1].T
R = [[r11, r12, r13],
[r21, r22, r23],
[r31, r32, r33]]
p2 = [x2,y2,z2].T
# 变换
p2 = R@p1 = [r11*x1 + r12*y1 + r13*z1, r21*x1 + r22*y1 + r23*z1, r31*x1 + r32*y1 + r33*z1].T
1. 旋转矩阵行代表的意义
对于一个旋转矩阵,其每一行表示p2的三轴坐标分别由p1的三轴坐标的多少分量组成。即:
第一行表示x1、y1、z1分别在x2上的分量,相乘相加即得x2坐标的值:
x2 = r11*x1 + r12*y1 + r13*z1
第二行表示x1、y1、z1分别在y2上的分量,相乘相加即得y2坐标的值:
y2 = r21*x1 + r22*y1 + r23*z1
第三行表示x1、y1、z1分别在z2上的分量,相乘相加即得z2坐标的值:
z2 = r31*x1 + r32*y1 + r33*z1
在三维视觉中,如果R表示相机在世界坐标系中的朝向信息,那么其每行对应于其每个轴在世界坐标系中的朝向。即通常的,第一行表示X轴朝向,第二行表示Y轴朝向,第三行表示Z轴朝向。
2. 旋转矩阵列代表的意义
其每一列表示p1的三轴坐标分别由p2的三轴坐标的多少分量组成。即:
第一列表示x1分别在x2、y2、z2上的分量,即:
x1 = r11*x2 + r21*y2 + r31*z2
第二列表示y1分别在x2、y2、z2上的分量,即:
y1 = r12*x2 + r22*y2 + r32*z2
第三列表示z1分别在x2、y2、z2上的分量,即:
z1 = r13*x2 + r23*y2 + r33*z2
其实上式就是p2 = R@p1的逆变换结果,即p1 = R.T@p2。可以自己动手推一下。
3. 关于R是单位正交阵的理解
根据旋转矩阵的定义,有:文章来源:https://www.toymoban.com/news/detail-786407.html
- 一个矩阵是旋转矩阵,当且仅当它是正交矩阵并且它的行列式是单位一。正交矩阵的行列式是 ±1;如果行列式是 −1,则它包含了一个反射而不是真旋转矩阵。
- 它在乘以一个向量的时候,有改变向量的方向但不改变大小的效果,并保持了手性。
我们知道,旋转矩阵的每一行、每一列的模长均为1。那么,为什么它的模长一定要是1呢?当然,一个理由是它就是这么定义的。实际上,旋转矩阵只是对向量进行了旋转,并不会对向量进行缩放,也就是旋转前后向量的长度应该是一样的。从上面说的旋转矩阵的行列意义可以直观看出这一点:将上述的点视为从坐标系原点出发的有向向量,那么,无论是正变换还是逆变换,变换前后坐标轴的分量模长之和总是1。文章来源地址https://www.toymoban.com/news/detail-786407.html
到了这里,关于深入理解三维旋转矩阵——R的行和列分别有什么含义的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!