笔记——Python数据结构与算法
一、栈和队列
1.1 栈的定义
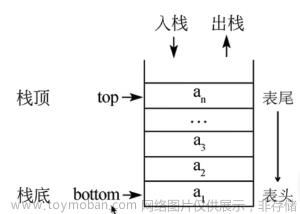
栈、队列、双端队列和列表都是有序的数据集合, 其元素的顺序取决于添加顺序或移除顺序。一旦某个元素被添加进来,它与前后元素的相对位置将保持不变。这样的数据集合经常被称为线性数据结构。
栈的添加操作和移除操作总发生在同一端。栈中的元素离底端越近,代表其在栈中的时间越长,因此栈的底端具有非常重要的意义。最 新添加的元素将被最先移除。这种排序原则被称作 LIFO(last-in first-out),即后进先出。它提供了一种基于在集合中的时间来排序的方式。最近添加的元素靠近顶端,旧元素则靠近底端。


1.2 栈的实现
代码实现:(注:定义栈顶位于列表末尾)
class Stack:
def __init__(self):
self.items = []
# 判断栈是否为空
def isEmpty(self):
return self.items == []
# 入栈,使用列表中的append方法
def push(self,item):
self.items.append(item)
# 出栈,使用列表中的pop方法
def pop(self):
return self.items.pop()
# 返回栈顶元素
def peek(self):
return self.items(len(self.items)-1)
# 返回栈的大小
def size(self):
return len(self.items)
## 栈的应用
a = Stack()
a.isEmpty()
>> True
a.push(4)
a.size()
>> 2
a.pop()
>> 4
1.3 应用案例一(括号匹配)
案例描述:从左到右读取一个括号串,然后判断其中的括号是否匹配。匹配括号是指每一个左括号都有与之对应的一个右括号,并且括号有正确的嵌套关系。下面是正确匹配的括号串:()()();((()))
解决思路:为了解决这个问题,需要注意到一个重要现象。当从左到右处理括号时,最右边的无匹配左括号 必须与接下来遇到的第一个右括号相匹配,如下图所示。并且,在第一个位置的左括号可能要 等到处理至最后一个位置的右括号时才能完成匹配。相匹配的右括号与左括号出现的顺序相反。这一规律暗示着能够运用栈来解决括号匹配问题。

# 导入Stack类
from pythonds.basic import Stack
# 定义括号匹配函数
def parCherker(symbolString):
# 实例化stack类
s = Stack()
# 设置balanced 为True 一个标志位
balanced = True
# 初始化序号0
index = 0
# 当index符合要求时,遍历symbolString
while index < len(symbolString) and balanced:
# 获取括号
symbol = symbolString[index]
# 如果是左括号压入堆栈
if symbol == '(':
s.push(symbol)
# 若是右括号则进一步判断
else:
# 如果堆栈为空,则设置标志位为False,跳出循环
if s.isEmpty():
balanced = False
# 否则返回栈顶括号,即遇到")"返回栈顶括号
else:
s.pop()
index = index + 1
# 所有括号匹配并且栈为空,返回TRUE
if balanced and s.isEmpty():
return True
else:
return False1.3 应用案例二(十进制转换)
案例描述: 利用栈将十进制转换为二进制
解决思路:如下图所示,每次将整数除以2然后取余,将所得余数压入栈中,随后出栈逆序输出。

def divideBy2(decNumber):
# 实例化堆栈
remstack = Stack()
# 判断为整数
while decNumber > 0:
# 除2取余
rem = decNumber %2
# 将其压入堆栈
remstack.push(rem)
# 取整数
decNumber = decNumber //2
# 初始化字符串
binString = ''
# 将堆栈的值逆序取出
while not remstack.isEmpty():
binString = binString + str(remstack.pop())
return binString二、队列
2.1 队列的定义
队列是有序集合,添加操作发生在“尾部”,移除操作则发生在“头部”(头删尾插)。新元素从尾部进入队列,然后一直向前移动到头部,直到成为下一个被移除的元素。最新添加的元素必须在队列的尾部等待,在队列中时间最长的元素则排在最前面。这种排序原则被称作 FIFO(first-in first-out),即先进先出,也称先到先得。队列的存储结构有顺序队或链队,主要以循环队列更为常见。根据其队列的存储方式的区别其实现方式也有所差异。

2.2 队列的常见应用
- 脱机打印输出:按申请的先后顺序依次输出。
- 多用户系统中,多个用户排成队,分时地循环使用CPU和主存。
- 按用户的优先级排成多个队,每个优先级一个队列
- 实时控制系统中,信号按接收的先后顺序依次处理
- 网络电文传输,按到达的时间先后顺序依次进行
2.3 队列的实现
def Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
# 在队头插入
def enqueue(self,item):
self.items.insert(0,item)
# 在队尾出栈
def dequeue(self):
return self.items.pop()
# 计算队列的大小
def size(self):
return len(self.items)
## 队列的操作
q = Queue()
q.isEmpty()
>> True
q.enqueue('dog')
q.enqueue(4)
q.enqueue(True)
q.size()
>> 3
q.deque()
>> 'dog'2.4 应用案例一(击鼓传花)
案例描述:该程序接受一个名字列表和一个用于计数的常 量 num,并且返回最后一人的名字。 我们使用队列来模拟一个环。假设握着土豆的孩子位于队列的头部。在模拟传土豆的过程中,程序将这个孩子的名字移出队列,然后立刻将其插入队列的尾部。随后,这个孩子会一直等待,直到再次到达队列的头部。在出列和入列 num 次之后,此时位于队列头部的孩子出局,新一轮游戏开始。如此反复,直到队列中只剩下一个名字(队列的大小为 1)。
解决思路:队列结构是一个循环队列的结构,即出列后的元素再进列
from pythonds.basic import Queue
# 传入两个参数,namelist和num
def hotPotato(namelist, num):
# 定义一个空列表
simqueue = Queue()
# 遍历namelist
for name in namelist:
# 将所有name传入队列中
simqueue.enqueue(name)
# 当队列中的元素大于1时,进行击鼓传花的游戏
while simqueue.size() >1:
# 进行num次循环
for i in range(num):
# 每次将头部出队列,在尾部加入队列
simqueue.enqueue(simqueue.dequeue())
# 当num次循环结束后,返回当前头部的队列
simqueue.dequeue()
return simqueue.dequeue()三、链表
3.1 链表的定义
在了解链表的定义之前,需要知道什么是链式存储结构,链式存储结构其结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻。链表就相当于无序列表。
为了实现无序列表,我们要构建链表。无序列表需要维持元素之间的相对位置,但是并不需要在连续的内存空间中维护这些位置信息。

需要注意的是,必须指明列表中第一个元素的位置。一旦知道第一个元素的位置,就能根据 其中的链接信息访问第二个元素,接着访问第三个元素,依此类推。指向链表第一个元素的引用被称作头。最后一个元素需要知道自己没有下一个元素。
3.2 链表的构建
节点(node)是构建链表的基本数据结构。每一个节点对象都必须持有至少两份信息。首先, 节点必须包含列表元素,我们称之为节点的数据变量。其次,节点必须保存指向下一个节点的引用。

注意,Node 的构造方法将 next 的初始值设为 None。由于这有时被称为“将节点接地”,因此我们使用接地符号来代表指向 None 的引用。将 None 作为 next 的初始值是不错的做法。
## 节点数据结构的构建
class Node:
# 初始化
def __init__(self,initdata):
self.data = initdata
self.next = None
# 查(每次需要设置两个部分)
def getData(self):
return self.data
def getNext(self):
return self.next
# 改(每次修改设置两个部分)
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext 链表是基于节点集合来构建的,每个节点都通过显示的引用指向下一个节点。只要知道第一个节点的位置(包括第一个节点包含第一个元素),其后的每个元素都能通过下一个引用找到。因此每次查找某个元素时,都需要从第一个元素开始寻找。

class UnorderedList:
def __init__(self):
self.head = None
def isEmpty(self):
return self.head == None
# 增
def add(self,item):
temp = Node(item)
temp.setNext(self.head) # 将新节点的末尾与头节点进行连接
self.head = temp # 将头节点设置为新加入的节点
# 计算长度
def length(self):
current = self.head
count = 0
while current != None:
count = count +1
current = current.getNext()
return count
# 查
def search(self,item);
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
current = current.getNext()
return found
# 删
def remove(self,item):
current = self.head # 头节点设置为current
previous = None # previous设置为None
found = False
while not found:
if current.getData() == item:
found = True # 检查当前节点中的元素是否为要移除的元素
else:
previous = current
current = current.getNext() # 进行蠕动
if previous == None: # 要删除的节点正好是头节点
self.head = current.getNext()
else: # 要删除的节点位于链表的中间
previous.setNext(current.getNext())
删除过程中必须先将previous移动到current的位置,然后再移动current。这一过程类似为"蠕动",previous必须在current向前移动之前指向当前位置。
3.3 有序列表的构建
在有序列表中,元素的相对位置取决于它们的基本特征。它们通常以升序或者降序排列,并 且我们假设元素之间能进行有意义的比较。
class OrderedList:
def __init__(self):
self.head = None
# 与无序列表相同
def isEmpty(self):
return self.head == None
def length(self):
current = self.head
count = 0
while current != None:
count = count +1
current = current.getNext()
return count
# 查
def search(self,item):
current = self.head
found = False
stop = False
while current != None and not found and not stop:
if current.getData() == item:
found = True
else:
if current.getData() > item:
stop = True
else:
current = current.getNext()
return found
# 增
def add(self,item):
current = self.head
previous = None
stop = False
while current != None and stop:
if current.getData() > item:
stop = True
else:
previous = current
current = current.getNext()
temp = Node(item)
if previous == None:
temp.setNext(self.head)
self.head = temp
else:
temp.setNext(current)
previous.setNext(temp)通过增加新的布尔型变量 stop,并将其初始化 为 False,可以将上述条件轻松整合到代码中。当 stop 是 False 时,我们可以继续搜索链表。如果遇到其值大于目标元素的节点,则将 stop 设为 True.从而不需要遍历完全部的链表。
四、搜索与排序
4.1 顺序搜索

从列表中的第一个元素开始,沿着默认的顺序逐个查看,直到找到目标元素或者查完列表。如果查看列表后仍然没有找到目标元素,则说明目标元素不在列表中。
def sequentialSearch(alist,item):
# 起始指针
pos = 0
# 设置一个found标志位
found = False
# 如果指针为超过列表长度并且还没有找到元素
while pos < len(alist) and not found :
if alist[pos] == item:
found = True
else:
pos = pos +1
return found时间复杂度为O(n)

4.2 二分搜索

二分搜索的首要条件是列表必须是有顺序的,即从小到大排列或者从大到小排列。二分搜索相较于顺序搜索,它的起始元素不是第一个元素,而是中间元素。其搜索逻辑如下:如果这个元素就是目标元素,那么就立即停止搜索;如果不是,则利用列表的有序性,排除一半元素,再在剩余一半的元素继续应用二分搜索,直至找到目标元素。
def binarySearch(alist,item):
# 头指针
first = 0
# 尾指针
last = len(alist) - 1
# 设置found标志位
found = False
# 循环操作,条件:如果还有搜索空间,并且没有找到
while first <= last and not found:
# 寻找中间二分点
midpoint = (first + last)//2
# 二分点对左右两边进行判断
if alist(midpoint) == item:
found = True
else:
# 如果目标元素比中间元素小,修改尾指针至中间元素的前一个元素
if item < alist[midpoint]:
last = midpoint -1
# 如果目标元素比中间元素大,修改头指针至中间元素的后一个元素
else:
first = midpoint +1
return found4.3 散列
4.3.1 散列表的定义
散列是元素的集合,其中一个元素以一种便于查找的方式存储。散列表中的每个位置通常被称为槽,其中可以存储一个元素。散列表的基本思想就是记录存储位置与存储关键字之间的对应关系,这个对应关系我们称之为哈希函数。
通过构建散列,我们可以得到一个时间复杂度为O(1)的数据结构。槽用一个从0开始的整数标记,例如0号槽,1号槽等。初始情形下,散列表中没有元素,每个槽都是空的。可以用列表来实现散列表,并将每个 元素都初始化为 Python 中的特殊值 None。

4.3.2 散列函数的定义
散列函数将散列表中的元素与其所属位置对应起来。对散列表中的任一元素,散列函数返回 一个介于 0和m – 1之间的整数。这个散列函数可以通过自定义编码的方式,将函数值和槽值对应起来。常见的散列函数是取余函数,具体算法如下:将整数元素除以表的大小,将得到的余数作为散列值。

4.3.3 散列表的冲突
显然,当每个元素的散列值是不同的情况下,这个散列表是完美的,但是如果散列值是相同的情况下,例如77和44,在散列表大小为11的情况下,散列值均为0,此时散列函数会将两个元素都放入同一个槽中,这种情况称作冲突。处理冲突是散列计算的重点,因为如果构建想要一个完美的散列表的话,任何一种散列函数所耗费的内存,在预估元素很多的情况下是相当大的。所以,我们需要解决好冲突问题,这样可以进一步降低所需内存。这里主要有两种办法。
一种方法是在散列表中找到另一个空槽,用于放置引起冲突的元素。简单的做法是从起初的 散列值开始,顺序遍历散列表,直到找到一个空槽。注意,为了遍历散列表,可能需要往回检查第一个槽。这个过程被称为开放定址法,它尝试在散列表中寻找下一个空槽或地址。由于是逐个访问槽,因此这个做法被称作线性探测。
另一种处理冲突的方法是让每个槽有一个指向元素集合(或链表)的引用。链接法允许散列 表中的同一个位置上存在多个元素。发生冲突时,元素仍然被插入其散列值对应的槽中。不过, 随着同一个位置上的元素越来越多,搜索变得越来越困难。图 5-12 展示了采用链接法解决冲突后的结果。

4.3.4 利用散列表来实现字典
字典是最有用的python集合之一,字典能根据给定的一个key,快速找到其关联的value,从而达到其高效搜索的实现方案。字典是存储键–值对的数据类型。键用来查 找关联的值,这个概念常常被称作映射。映射抽象数据类型定义如下。它是将键和值关联起来的无序集合,其中的键是不重复的,键和值之间是一一对应的关系。
# 初始长度为11的散列表的创建
class HashTable:
def __init__(self):
# 设置散列表的大小
self.size = 11
# 设置两个列表,一个存放键,一个存放值
self.slots = [None]*self.size
self.data = [None]*self.size
# 增,参数键值对
def put(self,key,data):
# 定义hashfunction为简单的取余函数,hashfunction返回的是散列值
hashvalue = self.hashfunction(key,len(self.slots))
# 如果散列表当前位置为空,则直接添加
if self.slots[hashvalue] == None:
# slots存放键,在列表的散列值处存放键
self.slots[hashvalue] = key
# data存放值,在列表的散列值处存放值,这样实现了键和值的一一对应(通过散列值)
self.data[hashvalue] = data
# 如果散列表当前位置不为空,有冲突
else:
# 如果键相同,值不同,则直接将原来的值修改,参考字典修改值的操作
if self.slots[hashvalue] == key:
self.data[hashvalue] = data
# 如果键不同,但是散列值相同
else:
# 再散列操作,定义一个nextslot变量
nextslot = self.rehash(hashvalue,len(self.slots))
# 如果再散列后的槽中的值不是空,并且键不相同,继续再散列操作
while self.slots[nextslot] != None and self.slots[nextslot] != key:
nextslot = self.rehash(nextslot,len(self.slots))
# 设置键值对
if self.slots[nextslot] == None:
self.slots[nextslot] = key
self.data[nextslot] = data
else:
self.data[nextslot] = data
# 取余哈希函数
def hashfunction(self,key,size):
return key%size
# 再哈希
def rehash(self,oldhash,size):
return (ordhash+1)%size
# 查
def get(self,key):
# 获取散列值
startslot = self.hashfunction(key,len(self.slots))
# 设置三个标志位
data = None
stop = False
found = False
position = startslot
# 如果当前当前散列值的槽不为空且没有找到也没有停止(因为有冲突的存在,所以有可能再散列)
while self.slots[position] != None and not found and not stop:
# 如果找到该键则跳出循环,返回data值
if self.slots[position] == key:
found = True
data = self.data[position]
# 如果键发生冲突,存在再散列操作
else:
# 再散列
position = self.rehash(position,len(self.slots))
if position == startslot:
stop = True
return data
def __getitem__(self,key):
return self.get(key)
def __setitem__(self,key,data):
return self.put(key,data)注:散列表的搜索效率是O(1),它是以一种空间换时间的数据结构。
4.4 冒泡排序
冒泡排序多次遍历列表。它比较相邻的元素,将不合顺序的交换。每一轮遍历都将下一个最 大值放到正确的位置上。本质上,每个元素通过“冒泡”找到自己所属的位置。

# 冒泡排序
def bubbleSort(alist):
# 左闭右开,逆序递减
for passnum in range(len(alist)-1,0,-1):
# 第一轮比较n-1对,最大的元素一直往前挪,直到遍历过程结束,逐轮递减
for i in range(passnum):
# 如果前一个元素比后一个元素大,则要进行转移数值的操作
if alist[i] > alist[i+1]:
temp = alist[i]
alist[i] = alist[i+1]
alist[i+1] = temp
4.5 选择排序
选择排序在冒泡排序的基础上做了改进遍历列表时只进行一次交换,选择排序在每次遍历时寻找最大值,并在遍历完之后将它放到正确位置上。和冒泡排序一样,每次遍历完后,当前最大的元素就位。

# 选择排序
def selectionSort(alist):
# 类似冒泡排序
for fillslot in range(len(alist)-1,0,-1):
# 初始化最大值标志位
positionofMax = 0
# 左闭右开,遍历未排序的整个序列,寻找最大值
for location in range(1,fillslot+1):
if alist[location] > alist[positionofMax]:
positionofMax = location
# 将最大值就位
temp = alist[fillslot]
alist[fillslot] = alist[positionofMax]
alist[positionofMax] = temp
# 时间复杂度与冒泡排序一致,均为o(n^2)4.6 插入排序
插入排序的时间复杂度也是 2 On ,但原理稍有不同。它在列表较低的一端维护一个有序的子列表,并逐个将每个新元素“插入”这个子列表。

# 插入排序
def insertionSort(alist):
for index in range(1,len(alist)):
# 获取当前指针和当前的元素值
currentvalue = alist[index]
position = index
# 如果当前指针大于0并且前一个元素值大于当前的元素值,那么需要调换操作
while position > 0 and alist[position-1] > currentvalue:
# 将前一个元素值与当前元素值交换
alist[position] = alist[position-1]
# 并且将指针做减一操作,尝试一直遍历到列表头
position = position-1
alist[position] = currentvalue4.7 归并排序
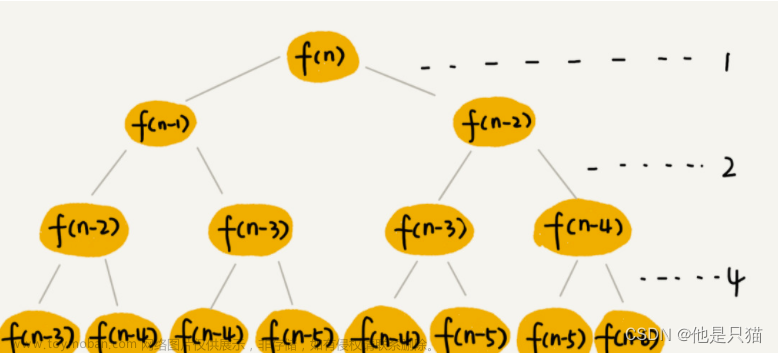
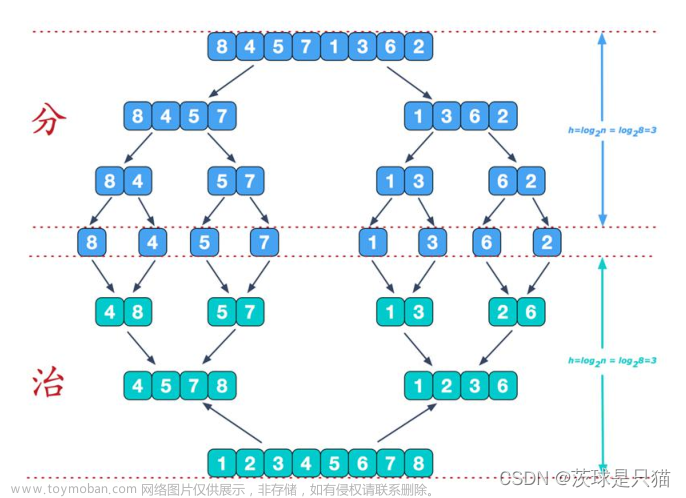
归并排序是递归算法,每次将一个列表一分为二。如果列表为空或只有一个元素,那么从定义上来说它就是有序的(基本情况)。如果列表不止一个元素,就将列表一分为二,并对两部分都递归调用归并。归并是指将两个较小的有序列表归并为一 个有序列表的过程。

def merge(alist,low,mid,high):
# 第一个有序列表的第一个元素
i = low
# 第二个有序列表的第一个元素
j = mid+1
ltmp = []
# 只要左右两个列表都有数
while i<=mid and j<=high:
# 比较两个列表当前指针的数的大小
if alist[i] < alist[j]:
# 先放入较小的那个
ltmp.append(alist[i])
# i+1
i+=1
else:
ltmp.append(alist[j])
j+=1
# while执行完,肯定有一部分是已经遍历完
# 如果第一个有序列表有数
while i<=mid:
ltmp.append(alist[i])
i +=1
# 如果第二个有序列表有数
while j<=high:
ltmp.append(alist[j])
j+=1
# 将ltmp传入alist
alist[low:high+1]=ltmp
# 归并操作,将列表越分越小,直至分为一个元素
def merge_sort(alist,low,high):
if low < high: # 至少有两个元素,递归;终止条件:只有一个元素
# 设置中间元素
mid = (low+high)//2
# 归并左边
merge_sort(alist,low,mid)
# 归并右边
merge_sort(alist,mid+1,high)
# 排序
merge(alist,low,mid,high)4.8快速排序
快速排序也是交换排序的一种,其原理是:将未排序的元素根据一个作为基准的“主元”分为两个子序列,其中一个子序列的记录均大于主元,而另一个子序列均小于主元,然后递归地对这两个子序列用类似的方法进行排序。本质上,快速排序使用分治法,将问题规模减小,然后再分别进行处理。


def quickSort(alist):
quickSoertHelper(alist,0,len(alist)-1)
def quickSoertHelper(alist,first,last):
if first < last: # 至少两个元素
# 递归
mid = partition(alist,first,last)
quickSort(alist,first,mid-1)
quickSort(alist,mid+1,last)
def partition(alist,left,right):
# tmp作为主元
tmp = alist[left]
# 如果之间还有两个元素
while left < right:
# 从右边找比temp小的数
while left < right and alist[right] >= tmp:
# 指针往左走一步
right -= 1
# 如果右边的值比主元小,则要换位置
alist[left] = alist[right]
# 在左边找比temp大的数
while left < right and alist[left] <= tmp:
left +=1
alist[right]=alist[left]
alist[left] = tmp
# 返回此时的主元位置
return left五、树
5.1 数的定义
数据的逻辑结构分为线性结构和非线性结构,上面我们提到的像栈、队列、线性表等均为线性结构;而这个树和图属于非线性结构。

树是n个节点的有限集。若n =0,称为空树;若n>0,则它满足如下两个条件:1、有且仅有一个特定的根称为根节点;2、其余结点可分为m个互不相交的有限集$T1,T2,T3...$,其中每个集合本身又是一棵树,并称为根的子树。因此可以看出来树的定义本身就是一个递归的过程,

5.2 二叉树的定义
二叉树不是树的特殊情况,而是两个概念。
二叉树结点的子树要区分左子树和右子树,即使只有一棵子树也要区分其是左子树还是右子树。
- 满二叉树
- 二叉树分类
- 二叉树的遍历
5.3 使用列表进行树的创建
在“列表之列表”的树 中,我们将根节点的值作为列表的第一个元素;第二个元素是代表左子树的列表;第三个元素是代表右子树的列表。

# 列表的列表进行树的定义
def BinaryTree(r):
return [r,[],[]]
# 添加左子树
def insertLeft(root,newBranch):
t = root.pop(1)
if len(t) > 1:
root.insert(1,[newBranch,t,[]])
else:
root.insert(1,[newBranch,[],[]])
return root
# 添加右子树
def insertRight(root,newBranch):
t = root.pop(2)
if len(t) > 1:
root.insert(2,[newBranch,[],t])
else:
root.insert(2,[newBranch,[],[]])
return root
# 树的访问函数
def getRootVal(root):
return root[0]
def setRootVal(root,newVal):
root[0] = newVal
def getLeftChild(root):
return root[1]
def getRightChild(root):
return root[2]5.4 二叉树的建立
二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间采用类似链表的链接方式来链接
class BiTreeNode:
def __init__(self,data):
# 设置根节点
self.key = data
# 设置左右子树
self.leftchild = None
self.rightchild = None
# 添加左子树
def insertLeft(self,newNode):
if self.LeftChild == None:
self.LeftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.left = self.LeftChild
self.LeftChild = t
# 添加右子树
def insertRight(self,newNode):
if self.rightchild == None:
self.rightchild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.right = self.rightchild
self.rightchild = t
# 实例一、构建二叉树,利用初始化类函数
a = BiTreeNode('A')
b = BiTreeNode('B')
c = BiTreeNode('C')
d = BiTreeNode('D')
e = BiTreeNode('E')
f = BiTreeNode('F')
g = BiTreeNode('G')
e.leftchild = a
e.rightchild = g
a.rightchild = c
c.leftchild = b
c.rightchild = d
g.rightchild = f
# 设置说明根节点为e
root = e
# 打印根节点的左子树的右子树的值
print(root.leftchild.rightchild.key)
# 返回结果
>> C上述实例一构建的二叉树模型如下图所示

5.5 二叉树的遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中所有节点,使得每个节点被访问一次且被访问一次。遍历方式分为以下三种:
1、前序遍历(根左右)
在前序遍历中,先访问根节点,然后递归地前序遍历左子树,最后递归地前序遍历右子树。

2、 中序遍历(左根右)
先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。

注:可以理解为将树从上往下拍扁,然后从左往右进行依次遍历
3、 后序遍历(左右根)
先递归地后序遍历右子树,然后递归地后序遍历左子树,最后访问根节点。

# 前序遍历
def pre_order(root):
if root:
print(root.key,end=',')
pre_order(root.leftchild)
pre_order(root.rightchild)
# 中序遍历
def in_order(root):
if root:
in_order(root.leftchild)
print(root.key,end=',')
in_order(root.rightchild)
# 后序遍历
def post_order(root):
if root:
post_order(root.leftchild)
post_order(root.rightchild)
print(root.key,end='')
## 遍历充分利用了递归的思想5.6 二叉搜索树
二叉搜索树具有如下特性:
1、若它的左子树不空,则左子树上所有结点的值均小于根节点的值;
2、若它的右子树不空,则右子树上所有结点的值均大于根节点的值;
3、它的左右子树也都是二叉排序树。
二叉搜索树的操作:查询、插入、删除
5.6.1 查找
查找的伪代码如下所示:
若二叉搜索树为空,则查找不成功;
否则:
1、若给定值等于根节点,则查找成功;
2、若给定值小于根节点,则继续在左子树上查找;
3、若给定值大于根节点,则继续在右子树上进行查找5.6.2 删除
删除的伪代码如下所示:
1、删除的结点是叶子节点
直接删除,然后修改其父节点的指针,置空即可。
2、 删除的结点有左子树和右子树
将其右子树的最小节点删除,并替换当前节点。
3、 删除的结点只有左子树或只有右子树
将此节点的父亲与孩子连接,然后删除该节点。5.6.3 代码实现
class BinarySearchTree:
def __init__(self,li=None):
self.root = None
self.size = 0
self.parent = None
if li:
for val in li:
self.insert_no_rec(val)
# 二叉搜索树的插入操作(使用递归)
def insert(self,node,val):
# 如果节点为可空
if not node:
node = BiTreeNode(val)
# 如果插入值小于节点,遍历左子树
elif val < node.key:
node.leftchild = self.insert(node.leftchild,val)
node.leftchild.parent = node
# 如果插入值大于节点,遍历右子树
elif val > node.key:
node.rightchild = self.insert(node.rightchild,val)
node.rightchild.parent = node
else:
return node
# 插入操作(不使用递归)
def insert_no_rec(self,key):
p = self.root
# 空树
if not p:
self.root = BiTreeNode(key)
return
while True:
# 如果插入节点比根节点小
if key < p.key:
# 如果左子树存在
if p.leftchild:
# 令p指针指向左子树
p = p.leftchild
# 如果左子树不存在
else:
# p的左子树为该插入节点
p.leftchild = BiTreeNode(key)
# 与父节点做链接
p.leftchild.parent = p
return
elif key > p.key:
if p.rightchild:
p = p.rightchild
else:
p.rightchild = BiTreeNode(key)
p.rightchild.parent = p
return
# 如果插入节点和根节点相同,则返回
else:
return
# 查询操作
def query(self,node,val):
if not node:
return None
if node.data < val:
return self.query(node.rchild,val)
elif node.data > val:
return self.query(node.leftchild,val)
else:
return node
# 查询操作非递归的方法
def query_no_rec(self,val):
p = self.root
while p:
if p.data < val:
p = p.rightchild
elif p.data > val:
p = p.leftchild
else:
return p
return None
# 删除操作
def delete(self,key):
p = None
q = self.root
# 当根节点不为空时,且添加的值不为根节点值时
while q and q.key != key:
# 将当前根节点指针赋予p
p = q
# 如果删除的值小于当前根节点,则往左子树搜索
if key < q.key:
# 将q指针指向q的左子树
q = q.leftchild
# 反之,往右子树搜索
else:
q = q.rightchild
if not q:
return
# 上面已经找到了要删除的节点,用q引用。而p则是q的父节点或者None。情况一、删除的节点没有左子树
if not q.leftchild:
# 如果删除节点的父节点是空,则要删除的是根节点,那么直接将其右节点设置为根节点
if p is None:
self.root = q.rightchild
# 如果要删除的节点是p的左子树,那么直接将p的左子树指向q的右子树
elif q is p.leftchild:
p.leftchild = q.rightchild
# 如果要删除的节点是p的右子树,那么直接将p的右子树指向q的右子树
else:
p.rightchild = q.rightchild
return
# 查找节点q的左子树的最右节点,将q的右子树链接为该节点的右子树
r = q.leftchild
# 查找到最小的右子树
while r.rightchild:
r = r.rightchild
r.rightchild = q.rightchild
if p is None:
self.root = q.leftchild
elif p.leftchild is q:
p.leftchild = q.leftchild
else:
p.rightchild = q.leftchild
# 三种遍历
def pre_order(self,root):
if root:
print(root.key, end=',')
pre_order(root.leftchild)
pre_order(root.rightchild)
def in_order(self,root):
if root:
in_order(root.leftchild)
print(root.key, end=',')
in_order(root.rightchild)
def post_order(self,root):
if root:
post_order(root.leftchild)
post_order(root.rightchild)
print(root.key, end='')六、图及其算法
6.1 图的定义
对于上面的树进行比较,图是更通用的结构,事实上,树可以看做一种特殊的图。图有多个前驱和多个后继。图可以理解为顶点和边的集合。

6.2 邻接矩阵
要实现图,最简单的方式就是使用二维矩阵。在矩阵实现中,每一行和每一列都表示图中的 一个顶点。第 v行和第 w列交叉的格子中的值表示从顶点 v到顶点 w的边的权重。如果两个顶点被一条边连接起来,就称它们是相邻的。

第v行和第w列交叉的格子中的值表示从顶点v到顶点w的边的权重,邻接矩阵总共大致分为以下三类。
1、无向图
对于n个顶点的无向图,其邻接矩阵是一个n×n的方阵。

2、有向图

3、加权图

6.3 图的实现
class Vertext(): # 包含了顶点信息,以及顶点连接边
def __init__(self,key):#key表示是添加的顶点
self.id = key
self.connectedTo = {} # 初始化临接列表
def addNeighbor(self,nbr,weight=0):# 这个是赋值权重的函数
self.connectedTo[nbr] = weight
def __str__(self):
return str(self.id)+ ' connectedTo: '+str([x.id for x in self.connectedTo])
def getConnections(self): #得到这个顶点所连接的其他的所有的顶点 (keys类型是class)
return self.connectedTo.keys()
def getId(self): # 返回自己的key
return self.id
def getWeight(self,nbr):#返回所连接ner顶点的权重是多少
return self.connectedTo[nbr]
'''
Graph包含了所有的顶点
包含了一个主表(临接列表)
'''
class Graph():# 图 => 由顶点所构成的图
'''
存储图的方式是用邻接表实现的.
数据结构: {
key:Vertext(){
self.id = key
self.connectedTo{
相邻节点类实例 : 权重
..
..
}
}
..
..
}
'''
def __init__(self):
self.vertList = {} # 邻接列表
self.numVertices = 0 # 顶点个数初始化
def addVertex(self,key):# 添加顶点
self.numVertices = self.numVertices + 1 # 顶点个数累加
newVertex = Vertext(key) # 创建一个顶点的临接矩阵
self.vertList[key] = newVertex
return newVertex
def getVertex(self,n):# 通过key查找定点
if n in self.vertList:
return self.vertList[n]
else:
return None
def __contains__(self,n):# transition:包含 => 返回所查询顶点是否存在于图中
#print( 6 in g)
return n in self.vertList
def addEdge(self,f,t,cost=0): # 添加一条边.
if f not in self.vertList: # 如果没有边,就创建一条边
nv = self.addVertex(f)
if t not in self.vertList:# 如果没有边,就创建一条边
nv = self.addVertex(t)
if cost == 0:# cost == 0 代表是没有传入参数,而使用的默认参数0,即是是无向图
self.vertList[f].addNeighbor(self.vertList[t],cost) # cost是权重.无向图为0
self.vertList[t].addNeighbor(self.vertList[f],cost)
else:#
self.vertList[f].addNeighbor(self.vertList[t],cost) # cost是权重
def getVertices(self):# 返回图中所有的定点
return self.vertList.keys()
def __iter__(self): #return => 把顶点一个一个的迭代取出.
return iter(self.vertList.values())
#
# -------------------------------------------------
# 以下是测试数据.可删除
# -------------------------------------------------
#
g = Graph()
# for i in range(6):
# g.addVertex(i)
# print(g.vertList)
'''
# a = g.vertList[0]
# print(a.connectedTo)
'''
g.addEdge(0,5,2)
g.addEdge(1,2,4)
g.addEdge(2,3,9)
g.addEdge(3,4,7)
g.addEdge(3,5,3)
g.addEdge(4,0,1)
g.addEdge(5,4,8)
g.addEdge(5,2,1)
print(g.getVertices())
# vertList = { key :VertextObject}
# VertextObject = ||key = key, connectedTo = {到达节点:权重}|| => |||| 表示的是权重的意思
# print(g)
for v in g: # 循环类实例 => return -> g = VertextObject的集合 v = VertextObject
for w in v.getConnections(): # 获得类实例的connectedTO
# print(w)
print("({},{}:{})".format(v.getId(),w.getId(),v.getWeight(w))) ## 为什么会是这样 => 因为这个时候v就是class啊6.4 图的遍历

图常用的遍历方式有两种,分别是深度优先搜索(DFS)和广度优先搜索(BFS)
6.4.1 深度优先搜索
深度优先其思想就是从图中某一个顶点出发,然后沿着边一直搜索,一条道走到黑!直到走投无路为止,然后再回退(迷途知返),当回退到能看到有尚未访问的顶点时,继续向前搜索,一条道走到黑。直到迷途知返回到顶点,且所有顶点均被访问为止,算法搜索结束。


from pythonds.graphs import Graph
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)6.4.2 广度优先搜索
广度优先类似于树的层次遍历,从图中的某个顶点出发,然后一次访问顶点未曾访问过的邻接点,然后从这些邻接点依次访问它们的邻接点。直至所有点被访问到


def bfs(g,start):
start.setDistance(0)
start.srtPred(None)
vertQueue = Queue()
vertQueue.enqueue(start)
while (vertQueue.size()>0):
currentVert = vertQueue.dequeue()
for nbr in currentVert.getConnections():
if (nbr.getColor() == 'white'):
nbr.setColor('gray')
nbr.setDistance(currentVert.getDistance()+1)
nbr.serPred(currentVert)
vertQueue.enqueue(nbr)
currentVert.setColor('black')七、参考资料
1、《python数据结构与算法》
2、清华大学博士讲解Python数据结构与算法(完整版)全套100节文章来源:https://www.toymoban.com/news/detail-786523.html
数据结构与算法文章来源地址https://www.toymoban.com/news/detail-786523.html
到了这里,关于Python数据结构与算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!