Prim算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了Prim算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前置知识：图的概念与性质

为了保证学习效果，请保证已经掌握前置知识之后，再来学习本章节！如果在阅读中遇到困难，也可以回到前面章节查阅。

引入

通过前面的学习，对于含有 n 个顶点的连通图来说可能包含有多种生成树，例如图 1 所示：

图 1 连通图的生成树

图 1 中的连通图和它相对应的生成树，可以用于解决实际生活中的问题：假设A、B、C 和 D 为 4 座城市，为了方便生产生活，要为这 4 座城市建立通信。对于 4 个城市来讲，本着节约经费的原则，只需要建立 3 个通信线路即可，就如图 1（b）中的任意一种方式。

在具体选择采用（b）中哪一种方式时，需要综合考虑城市之间间隔的距离，建设通信线路的难度等各种因素，将这些因素综合起来用一个数值表示，当作这条线路的权值。

prim算法的,数据结构&算法,算法,图论,数据结构

图 2 无向网

假设通过综合分析，城市之间的权值如图 2（a）所示，对于（b）的方案中，选择权值总和为 7 的两种方案最节约经费。

这就是本节要讨论的最小生成树的问题，简单得理解就是给定一个带有权值的连通图（连通网），如何从众多的生成树中筛选出权值总和最小的生成树，即为该图的最小生成树。

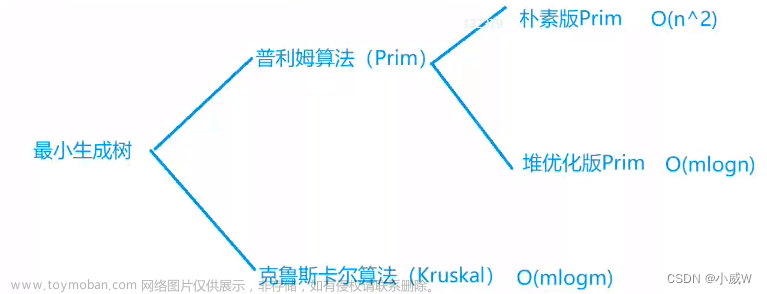
给定一个连通网，求最小生成树的方法有：普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。

普里姆算法

一种贪心的算法，适用于稠密图，时间复杂度 O(n^2)O(n2)。

核心思想：每次挑一条与当前集合相连的距离最近的点。

原理

普里姆算法在找最小生成树时，将顶点分为两类，一类是在查找的过程中已经包含在树中的（假设为 A 类），剩下的是另一类（假设为 B 类），并且 Prim 算法总是维护最小生成树的一部分，类似 Dijkstra 算法。

对于给定的连通网，起始状态全部顶点都归为 B 类。在找最小生成树时，选定任意一个顶点作为起始点，并将之从 B 类移至 A 类；然后找出 B 类中到 A 类中的顶点之间权值最小的顶点，将之从 B 类移至 A 类，如此重复，直到 B 类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。

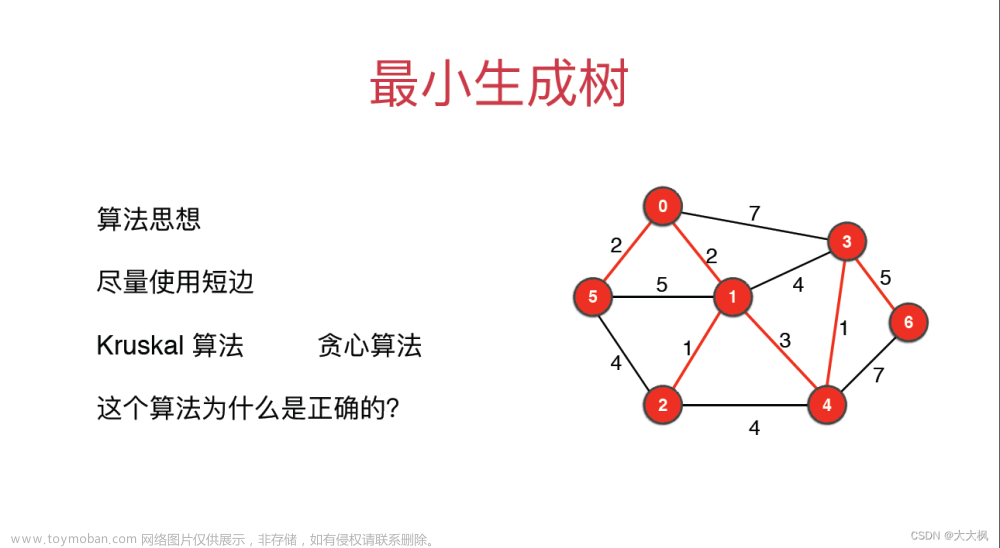
切分定理

❓为什么每次选最小边是正确的呢

Prim 算法是基于切分定理的。

切分（Cut）：把图中的节点分为两部分，称为一个切分。下图有个切分 C = (S, T)，S = {A, B, D}，T = {C, E}

prim算法的,数据结构&算法,算法,图论,数据结构

横切边（Crossing Edge）：如果一个边的两个顶点，分别属于切分的两部分，这个边称为横切边。比如上图的边 BC、BE、DE 就是横切边。
切分定理：给定任意切分，横切边中权值最小的边必然属于最小生成树。
- 证明：假设原图切分后的两个部分各自组成了一棵最小生成子树，那么在这两个部分之间加入任意一条边都可以将形成整个图的生成树。很容易得知，加入所有横切边中权值最小的边就可以形成最小生成树。

算法过程

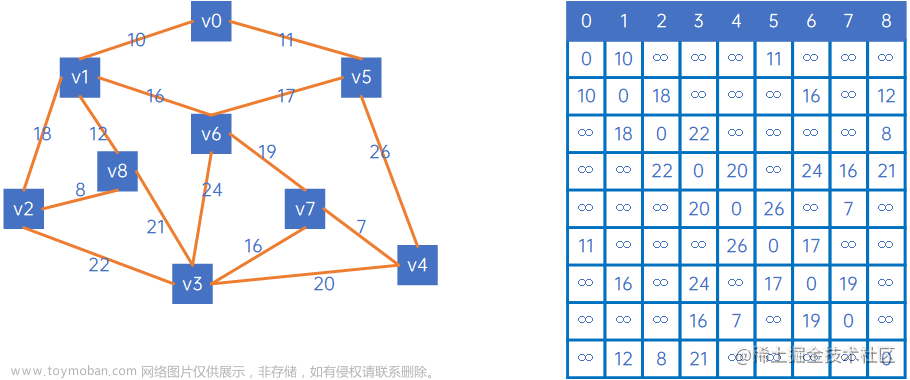
例如，通过普里姆算法查找图 2（a）的最小生成树的步骤为：

假如从顶点A出发，顶点 B、C、D 到顶点 A 的权值分别为 2、4、2，所以，对于顶点 A 来说，顶点 B 和顶点 D 到 A 的权值最小，假设先找到的顶点 B：

prim算法的,数据结构&算法,算法,图论,数据结构

继续分析顶点 C 和 D，顶点 C 到 B 的权值为 3，到 A 的权值为 4；顶点 D 到 A 的权值为 2，到 B 的权值为无穷大（如果之间没有直接通路，设定权值为无穷大）。所以顶点 D 到 A 的权值最小：

prim算法的,数据结构&算法,算法,图论,数据结构

最后，只剩下顶点 C，到 A 的权值为 4，到 B 的权值和到 D 的权值一样大，为 3。所以该连通图有两个最小生成树：

prim算法的,数据结构&算法,算法,图论,数据结构

示例代码

具体实现代码为：

/*
S:当前已经在联通块中的所有点的集合
1. dis[i] = inf
2. for n 次
    t<-S外离S最近的点
    利用t更新S外点到S的距离
    st[t] = true
n次迭代之后所有点都已加入到S中
联系：Dijkstra算法是更新到起始点的距离，Prim是更新到集合S的距离
*/
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;

int n, m;
int g[N][N], dis[N];
//邻接矩阵存储所有边
//dis存储其他点到S的距离
bool st[N];

int prim() {
    // 如果图不连通返回 0x3f3f3f3f, 否则返回 res
    memset(dis, 0x3f, sizeof dis);
    dis[1] = 0;
    int res = 0;

    for(int i = 0; i < n; i++) {
        int t = -1;
        for(int j = 1; j <= n; j++)  // 寻找离集合S最近的点 
            if(!st[j] && (t == -1 || dis[t] > dis[j]))
                t = j;
                // 不连通，无最小生成树
        if(i && dis[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
        res += dis[t];
        st[t] = true;
        //最新所有点到 S 的距离，注意和 dijkstra 对比，不是路径权值和
        for(int j = 1; j <= n; j++)
                    dis[j] = min(dis[j], g[t][j]);
    }
    return res;
}

int main() {
    cin >> n >> m;
    int u, v, w;

    memset(g, 0x3f, sizeof g);
    for(int i = 1; i <= n; i++)
        g[i][i] = 0;

    while(m--) {
        cin >> u >> v >> w;
        g[u][v] = g[v][u] = min(g[u][v], w);
    }
    int t = prim();
    if(t == 0x3f3f3f3f) puts("impossible");
    else cout << t << endl;
}

Copy

时间复杂度

普里姆算法的运行效率只与连通网中包含的顶点数相关，而和网所含的边数无关。所以普里姆算法适合于解决边稠密的网，该算法运行的时间复杂度为：O(n^2)O(n2)。

如果连通网中所含边的绸密度不高，则建议使用克鲁斯卡尔算法求最小生成树。

堆优化的Prim算法

堆prime的优化，主要从for循环里的两个for循环下手：

第一个for循环是找最小值，方式使用堆进行优化；

对第二个for循环，用邻接表进行操作。

思路

如果使用二叉堆，prim算法的复杂度能降到O(E log V)。

之前实现的这个Prim算法，是用邻接矩阵表示图。而堆优化的Prim算法，将用邻接表来表示图，且使用最小堆来寻找，连接MST集合和非MST集合的边中，最小权值的那条边。

基本思想：基本思想和原Prim算法大体相同，但此算法是，根据邻接表，通过广度优先遍历（BFS）来遍历所有节点，遍历的总操作为O(V+E)次数。同时使用最小堆存储非MST集合中的节点，每次遍历时用最小堆来选择节点。最小堆操作的时间复杂度为O(LogV)。

基本步骤

创建一个大小为V的最小堆，V是图的节点个数。最小堆的每个元素，存储的是节点id和节点的key值。
初始化时，让堆的第一个元素作为最小生成树的根节点，赋值根节点的key值为0。其余节点的key值赋值为无穷大。 3.只要最小堆不为空，就重复以下步骤： (i)从最小堆中，抽取最小key值的节点，作为u。 (ii)对于u的每个邻接点v，检查v是否在最小堆中（即还没有加入到MST中）。如果v在最小堆中，且v的key值是大于边u-v的权值时，就更新v的key值为边u-v的权值。

示例代码

#include <cstring>
#include <iostream>
#include <queue>
using namespace std;

const int MAXN = 510, MAXM = 2 * 1e5 + 10, INF = 0x3f3f3f3f;
typedef pair<int, int> PII;
int h[MAXM], e[MAXM], w[MAXM], ne[MAXM], idx;
bool vis[MAXN];
int n, m;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int Prim()
{
    memset(vis, false, sizeof vis);
    int sum = 0, cnt = 0;
    priority_queue<PII, vector<PII>, greater<PII>> q;
    q.push({0, 1});

    while (!q.empty())
    {
        auto t = q.top();
        q.pop();
        int ver = t.second, dst = t.first;
        if (vis[ver]) continue;
        vis[ver] = true, sum += dst, ++cnt;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (!vis[j]) {
                q.push({w[i], j});
            }
        }
    }

    if (cnt != n) return INF;
    return sum;
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 0; i < m; ++i)
    {
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
        add(b, a, w);
    }

    int t = Prim();
    if (t == INF) cout << "impossible" << endl;
    else cout << t << endl; 
}

Copy

时间复杂度

使用二叉堆，prim算法的复杂度降到了 O(E log V)。

对比两种最小生成树算法

Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。 1. 把图中的所有边按代价从小到大排序； 2. 把图中的n个顶点看成独立的n棵树组成的森林； 3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。 4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

适用于稀疏图，代码实现简洁。