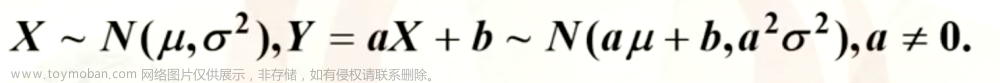正态分布的极大似然估计

8月前作者：Uncertainty!! 分类：Toy博客阅读(77) 违法举报

这篇具有很好参考价值的文章主要介绍了正态分布的极大似然估计。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 正态分布的极大似然估计

笔记来源：Maximum Likelihood For the Normal Distribution, step-by-step!!!

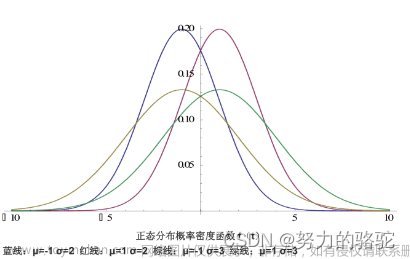
1.1 正态分布的参数对其形状的影响

1.1.1 μ值对正态分布的影响

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

1.1.2 σ值对正态分布的影响

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

1.2 极大似然估计

极大似然估计提供了一种给定观察数据来评估模型参数的方法【引用自：一文搞懂极大似然估计】

P(所求 | 已知)、L(所求 | 已知)
概率是已知模型和参数，推数据 $P(x|\mu,\sigma)$

统计是已知数据，推模型和参数 $L(\mu,\sigma|x)$ 【引用自：详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解】

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

我们简单的计算一下某个数据32在两个正态分布下的似然值
$L(\mu=28，\sigma=2\ |\ x=32)\\ L(\mu=30，\sigma=2\ |\ x=32)$

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

寻找极大似然估计的流程解释：
1.固定标准差，改变均值，计算出所给数据在正态分布（标准差相同、均值不同）下的似然值，绘制均值似然值函数图像，函数图像导数为0的地方就是均值的极大似然
2.将第一步中找到的均值最大似然固定下来，这次我们只改变标准差，计算出所给数据在正态分布（均值相同、标准差不同）下的似然值，绘制标准差似然值函数图像，函数图像导数为0的地方就是标准差的极大似然

因为要完成上面流程需要大于1个观测数据，但为了解极大似然估计图像如何绘制，我们这里先以一个数据来展示

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布
寻找最优标准差需要大于1个数据

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

接下来进入正题：计算n个数据的极大似然估计

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布
为方便处理，我们将上式两端同时取对数
取对数不改变极值的位置

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

首先对上面的等式求 $\mu$ 的偏导（将 $\mu$ 视为变量，将 $\sigma$ 视为常数），然后令其等于0，找到均值的极大似然估计

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布

上面我们找到了均值的极大似然估计，接下来上面的等式求 $\sigma$ 的偏导（将 $\sigma$ 视为变量，将 $\mu$ 视为常数），找到标准差的极大似然估计

正态分布的极大似然估计,# 概率与数理统计,概率论,极大似然估计,MLE,正态分布文章来源地址https://www.toymoban.com/news/detail-787717.html

到了这里，关于正态分布的极大似然估计的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

标准正态分布的概率密度函数和累积分布函数

标准正态分布概率密度函数：累积分布函数：图像：

2024年02月11日
浏览(178)
基于python/scipy学习概率统计(3)：正态分布

目录 1. 前言 2. 概率密度函数(PDF: Probability Density Function)¶ 3. 累积分布函数(CDF: Cumulative Distribution Function) 4. 百分点函数(PPF: Percent Point Function) 5. 生成函数和风险函数 6. 常用统计特征 7. 应用示例 7.1 从正态分布中采样 7.2 The 68-95-99.7 Rule 8. Why is the normal distribution useful and importan

2023年04月08日
浏览(77)
python绘制二维正态分布概率密度图（2d,3d）

2024年02月04日
浏览(30)
正态分布t个标准差范围内的概率

如果一个随机变量具有概率密度函数 f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , − ∞ x ∞ begin{aligned} f(x)=frac{1}{sqrt{2pi} sigma} e^{-frac{(x-mu)^2}{2sigma^2}}, quad -infty x infty end{aligned} f ( x ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2 , − ∞ x ∞ 则称X为正态随机变量并记为 X ∼ N

2024年02月07日
浏览(47)
【小呆的概率论学习笔记】正态分布的代数运算

0. 正态分布简介正态分布应该是概率论和数理统计中最重要的一类概率分布，最早的完整论述是由数学王子高斯提出，高斯主要用来分析观测的误差分析中推导出正态分布。虽然随着概率统计学的发展，自然分布形式多种多样，但是正态分布仍然可以说是最重要的自然分布。

2024年02月11日
浏览(43)
概率论与数理统计：正态分布相关推论及推导（更新ing）

统计量： X ‾ = 1 n ∑ i = 1 n X i ，其中 X i ~ N ( μ , σ 2 ) overline{X}= cfrac{1}{n}sum_{i=1}^nX_{i}，其中X_{i}text{textasciitilde} N(mu,{sigma^{2}} ) X = n 1 i = 1 ∑ n X i ，其中 X i ~ N ( μ , σ 2 ) S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^2= cfrac{1}{n-1}sum_{i=1}^n(X_{i}-overline{X})^2 S 2 = n −

2024年02月07日
浏览(34)
概率论之证明正态分布的上a 分位点的对称的性质

公式(Z(a) = -Z(1-a)) 表示正态分布的上(a)分位点与下(1-a)分位点在分布曲线上关于均值的对称性。左侧 (Z(a))：这是分布曲线上累积概率为(a)的那个点。也就是说，这是一个使得这个点及其左侧的面积占据整个曲线下方(a)的位置。右侧 (Z(1-a))：这是分布曲线上累积概率为(1-a)的

2024年01月15日
浏览(27)
人工智能数学基础--概率与统计13：连续随机变量的标准正态分布

一、引言在《人工智能数学基础–概率与统计12：连续随机变量的概率密度函数以及正态分布》介绍了连续随机变量概率分布及概率密度函数的概念，并介绍了连续随机变量一个重要的概率密度函数：正态分布的概率密度函数的定义以及推导、使用场景，本文将介绍连续随机

2023年04月25日
浏览(34)
【概率论与数理统计】猴博士笔记 p41-44 统计量相关小题、三大分布的判定、性质、总体服从正态分布的统计量小题

题干：总体X 有一些样本X1、X2、X3… 解法：注意，S的分母是 n-1 接下来练习套公式：例1：直接背公式。例2：解：除X，S，n外有其他位置数的就不是统计量。则，D。例3：解：用到的考点：还有正态分布的方差。答案：n-1 题型如下：题解：只有三种分布： X（卡方）

2023年04月08日
浏览(44)
概论_第3章_正态分布的重要结论__正态分布与标准正态分布关系

在两个随机变量的函数这一章节，会涉及到正态分布。一. 二. 若X, Y相互独立， X~N(), Y~N(), 则 aX+bY+c ~ N( ) . 特别注意相加后，不用加c 注意以下推理： 1， X 服从正态分布， Y 服从正态分布， X+Y 不一定服从正态分布举例： Y= -X, 则X+Y=0, 就

2024年02月03日
浏览(52)