深度学习
必备的数学知识
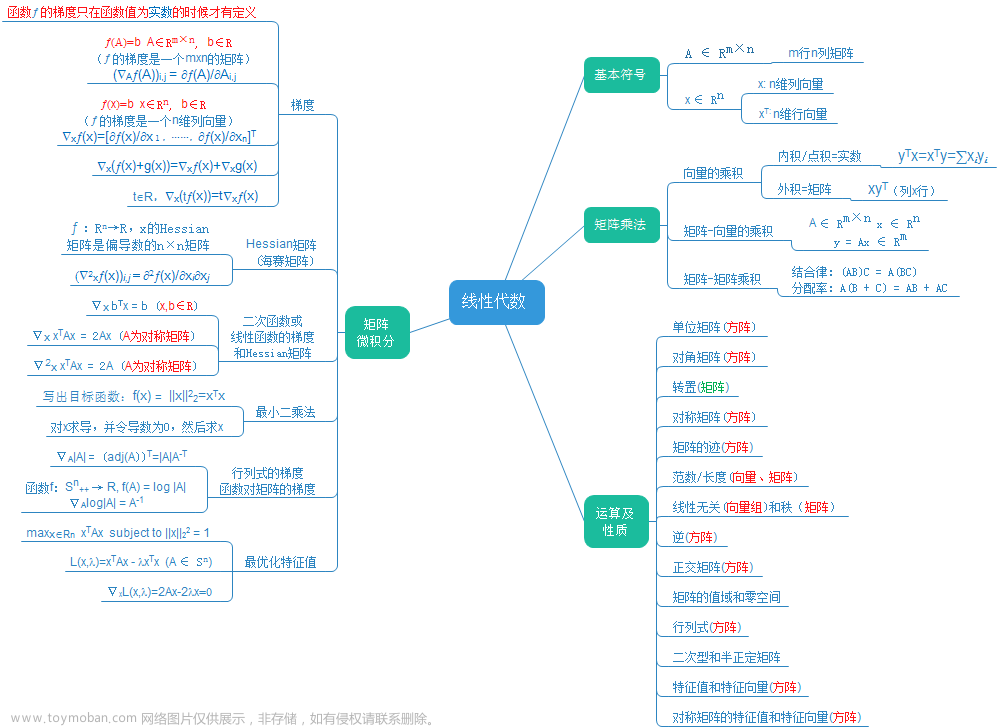
线性代数
在数学中,分解通常指的是将一个复杂的对象或结构分解为更简单的部件或组件。这个概念在许多数学领域都有应用。在线性代数中,矩阵分解是常见的一个主题,我们通过分解矩阵来发现它不明显的性质。
矩阵有许多种的分解方式:LU分解、QR分解、特征分解、奇异值分解等
这篇文章将会讲解其中的两种分解方式:特征分解、奇异值分解。
特征分解
矩阵的特征分解是指将矩阵分解成一组特征向量和一组特征值。
满足
A
v
=
λ
v
\mathbf{A}\mathbf{v}=\lambda\mathbf{v}
Av=λv
的向量
v
\mathbf{v}
v称为右特征向量(right eigenvector),特征向量与矩阵相乘相当于对于它自身进行缩放。标量
λ
\lambda
λ称为特征值(eigenvalue)。需要注意的是,特征向量是非零向量。
满足
v
T
A
=
v
λ
\mathbf{v}^T\mathbf{A}=\mathbf{v}\lambda
vTA=vλ
的特征向量称为左特征向量(left eigenvector);
在线性代数中,我们通常讨论的是右特征向量。
矩阵分解的目标是将找到一组线性无关的特征向量作为新的基(基是一个向量空间中的一组线性无关的向量,它们可以组合起来生成整个向量空间)。在这个基下,原矩阵可以被表示为一个
d
i
a
g
(
v
)
diag(\mathbf{v})
diag(v)。其中
v
\mathbf{v}
v是由特征值组成的向量。
并不是所有的矩阵都可以进行特征分解,主要是因为并不是每一个矩阵都由足够的线性无关的特征向量来构成一个完整的基。有些矩阵的特征分解还涉及到了复数。但是如果一个矩阵是对称的,那么它总是可以被特征分解,这桑因为对称矩阵总是可以找到一个由其特征向量构成的正交基。
对于每一个实对称矩阵,可以将它分解成实特征向量和实特征值:
A
=
Q
Λ
Q
T
\mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^T
A=QΛQT
其中矩阵
Q
\mathbf{Q}
Q是由特征向量为列向量组成的正交矩阵,矩阵
Λ
\mathbf{\Lambda}
Λ是以特征值为对角元素的对角矩阵。特征向量
Q
:
,
i
Q_{:,i}
Q:,i对应的特征值是
Λ
i
,
i
\Lambda_{i,i}
Λi,i。
让我们详细看一下这个式子。这个式子分两步运算:
第一步:计算
Q
Λ
\mathbf{Q}\mathbf{\Lambda}
QΛ,这一步将
A
\mathbf{A}
A 从原来的坐标系转换到特征向量构成的新坐标系中的对角矩阵。
第二步:计算(
Q
Λ
\mathbf{Q}\mathbf{\Lambda}
QΛ)
Q
T
\mathbf{Q}^T
QT 。乘以
Q
T
\mathbf{Q}^T
QT是将第一步得到的新坐标转换为原来的坐标。
特征分解可以被视为一种坐标系的转换。在特征分解中,我们找到一组新的基向量(即特征向量),这些基向量定义了一个新的坐标系。在这个新的坐标系中,原矩阵被表示为一个对角矩阵,其对角线上的元素是特征值。这个对角矩阵在新的坐标系中更容易处理,因为它只在对角线上有非零元素。所以,特征分解可以被看作是从原坐标系到特征向量定义的新坐标系的转换。
通过特征分解我们可以知道很多关于矩阵的信息:
- 矩阵是奇异的,当且仅当它含有零特征值
- 实对称矩阵的特征分解可以用于优化二次方程 f ( x ) = x T A x f(x)=x^T\mathbf{A}x f(x)=xTAx,其中现在 ∣ ∣ x ∣ ∣ 2 = 1 ||x||_2=1 ∣∣x∣∣2=1。如果 x \mathbf{x} x等于 A \mathbf{A} A的某个特征向量时, f f f将返回对应的特征值。在限制条件下,函数 f f f的最大值是最大特征值,最小值是最小特征值。
如果一个矩阵的所有特征值都是正数,则称为正定(positive definite);所有特征值都是非负数,则称为半正定(positive semidefinite);所有特征值都是负数,则称为负定(negative definite);所有特征值都是非正数,则称为半负定(negative semidefinite)。文章来源:https://www.toymoban.com/news/detail-787797.html
奇异值分解
奇异值分解(singular value decomposition,SVD)是将矩阵分解成奇异向量(singular)和奇异值(singular value)。每一个实数矩阵都有一个奇异值分解。奇异值分解可以让我们得到一些与特征分解相同的信息。
我们将矩阵
A
\mathbf{A}
A分解成三个矩阵的乘积
A
=
U
D
V
T
\mathbf{A}=\mathbf{U}\mathbf{D}\mathbf{V}^T
A=UDVT
矩阵
U
\mathbf{U}
U和
V
\mathbf{V}
V被定义为正交矩阵,矩阵
V
\mathbf{V}
V是对角矩阵。
如果
A
\mathbf{A}
A是一个m行n列的矩阵,则
U
\mathbf{U}
U是一个m行m列的方阵,
D
\mathbf{D}
D是一个m行n列的矩阵,
V
\mathbf{V}
V是一个n行n列的方阵。
矩阵
U
U
U的列向量称为左奇异向量(left singular vector),它是
A
A
T
\mathbf{A}\mathbf{A}^T
AAT的特征向量;矩阵
V
\mathbf{V}
V的列向量被称为右奇异向量(right singular vector) ,它是
A
T
A
\mathbf{A}^T\mathbf{A}
ATA的特征向量;矩阵
D
\mathbf{D}
D的对角元素称为矩阵
A
\mathbf{A}
A的奇异值(singular value),非零奇异值是
A
T
A
\mathbf{A}^T\mathbf{A}
ATA特征值的平方根,同时也是
A
A
T
\mathbf{A}\mathbf{A}^T
AAT的平方根。文章来源地址https://www.toymoban.com/news/detail-787797.html
到了这里,关于深度学习-必备的数学知识-线性代数5的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!