层次分析法

人们常常面临一个由 相互关联、相互制约的众 多因素构成的复杂而往往 缺少定量数据的系统；
AHP是对一些较为复杂、较为模糊的问题作出决策的简易方法，特别适用于那些难于完全定量分析的问题；
美国运筹学家T. L. Saaty 教授于上世纪70 年代初期提出的一种简便、灵活而又实用的 多准则决策方法。

1.层次分析法的基本原理与步骤

---

• 建立递阶层次结构模型；
• 构造出各层次中的所有 判断矩阵；
• 层次单排序及 一致性检验；
• 层次总排序及一致性检验。

1.1 递阶层次结构的建立与特点

---

最高层（ 目标层）：只有 一个元素，是分析问题的 预定目标或理想结果；
中间层（ 准则层）：为实现目标所涉及的中间环节，可以由若干个层次组成，包括 所需考虑的准则、子准则；
最底层（ 措施层）：为实现目标可供选择的 各种措施、决策方案等，也称为方案层。
层次数与问题的复杂程度及需要分析的详尽程度有关，一般层次数不受限制。每一层次中各元素所支配的元素一般不超过9个。

例：

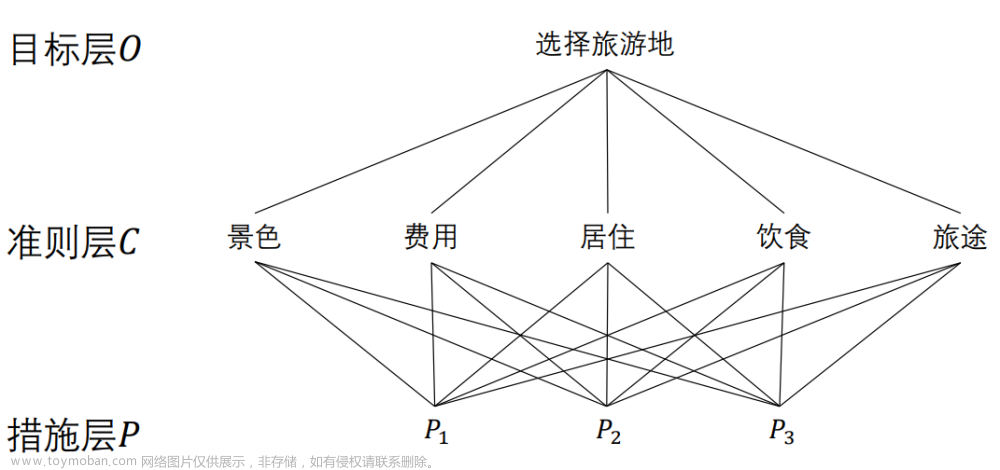
假期旅游有3个旅游胜地𝑃1, 𝑃2, 𝑃3供你选择，试确定一个最佳地点。

1.2 构造判断矩阵

---

在确定影响某因素的诸因子所占的比重时，这些比重常常不易定量化；
因子较多时，决策者常常会因考虑不周全提出与他实际认为的重要性程度不相一致的数据。
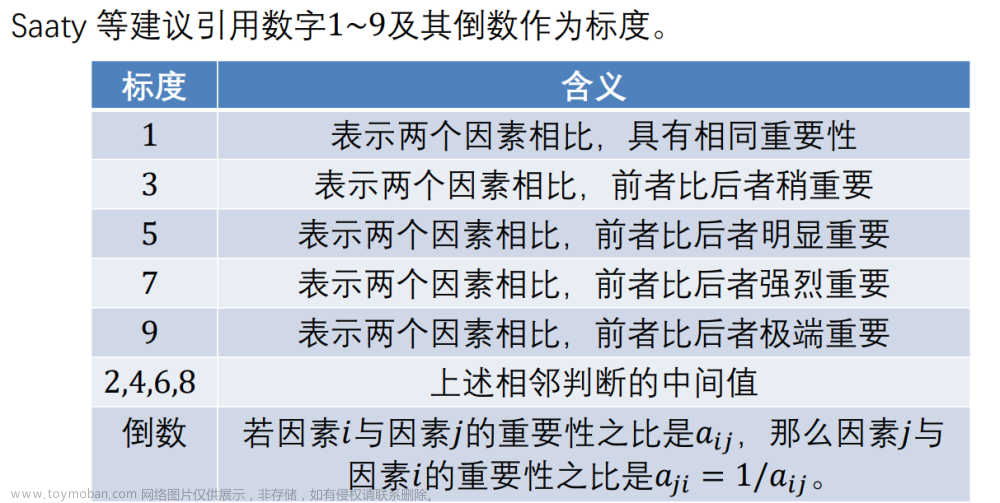
Saaty 等建议可以采取对因子进行 两两比较建立成对比较判断矩阵的办法。

成对比较判断矩阵

1.3 层次单排序及一次性检验

---

层次单排序：判断矩阵𝐴对应于最大特征值𝜆𝑚𝑎𝑥的特征向量𝑊，经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值。

• 减少其它因素的干扰，较客观地反映出一对因子影响力的差别；

• 但综合全部比较结果时，其中难免包含一定程度的非一致性。

➢ 如果比较结果是前后完全一致的，则矩阵A 的元素还应当满足： 𝑎𝑖𝑗𝑎𝑗𝑘 = 𝑎𝑖𝑘，∀𝑖,𝑗, 𝑘 = 1,2, … 𝑛 满足关系式的正互反矩阵称为一致矩阵。 需要检验构造出来的正互反判断矩阵𝐴是否严重地非一致，以便确定是否接受𝐴。

定理1：

正互反矩阵𝐴的最大特征根𝜆𝑚𝑎𝑥必为正实数，其对应特征向量的所有分量均为正实数。𝐴的其余特征值的模均严格小于𝜆𝑚𝑎𝑥。

定理2：

若𝐴为一致矩阵，则
（1）𝐴必为正互反矩阵；
（2）𝐴的转置矩阵𝐴 𝑇也是一致矩阵；
（3）𝐴的任意两行成比例，比例因子大于零，从而𝑟𝑎𝑛𝑘(𝐴) = 1（任意两列类似）；
（4）𝐴的最大特征值 𝜆𝑚𝑎𝑥 = 𝑛，其中𝑛为矩阵𝐴的阶。𝐴的其余特征根均为0；
（5）若A 的最大特征值𝜆𝑚𝑎𝑥对应的特征向量为𝑊 = (𝑤1, . . , 𝑤𝑛)^ 𝑇 ，则𝑎𝑖𝑗 = 𝑤𝑖 / 𝑤𝑗

定理3：

𝑛阶正互反矩阵𝐴为一致矩阵当且仅当其最大特征根 𝜆𝑚𝑎𝑥 = 𝑛，且当正互反矩阵𝐴非一致时，必𝜆𝑚𝑎𝑥 > 𝑛。

• 可由𝜆𝑚𝑎𝑥是否等于𝑛来检验判断矩阵𝐴是否为一致矩阵；

• 𝜆𝑚𝑎𝑥比𝑛大得越多，𝐴的非一致性程度也就越严重，𝜆𝑚𝑎𝑥对应的标准化特征向量也就越不能真实地反映出 𝑋 = {𝑥1, … 𝑥𝑛}在对因素𝑍的影响中所占的比重。

➢ 作一次一致性检验，以决定是否能接受它。

一次性检验的步骤

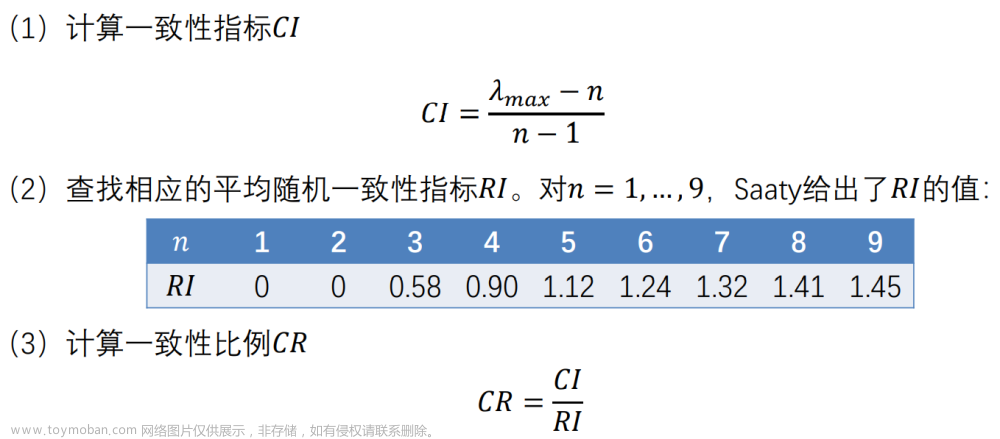
Saaty的𝑅𝐼值的取法：

• 用随机方法构造500个样本矩阵；

• 随机地从1~9及其倒数中抽取数字构造正互反矩阵；

• 求得最大特征根的平均值𝜆′ 𝑚𝑎𝑥；

𝑅𝐼 = (𝜆′ 𝑚𝑎𝑥 − 𝑛) / (𝑛 − 1)

➢ 当𝐶𝑅 < 0.10时，认为判断矩阵的一致性是可以接受的，否则应对判断矩阵作适当修正。

1.4 层次总排序及一致性检验

---

我们最终要得到各元素，特别是最低层中各方案对于目标的排序权重，从而进行方案选择。总排序权重要自上而下地将单准则下的权重进行合成。

• 上层(𝐴层)包含𝐴1, 𝐴2, … 𝐴𝑚共𝑚个因素，层次总排序权重为𝑎1, 𝑎2, … 𝑎𝑚；
• 下层(𝐵层)包含𝐵1, 𝐵2, … 𝐵𝑛共𝑛个因素，关于𝐴𝑗的层次单排序权重为𝑏1𝑗 , 𝑏2𝑗 , … 𝑏𝑛𝑗； 则𝐵层各因素关于总目标的权重，即各因素的层次总排序权重为：

2.层次分析法的应用

---

2.1 两个困难

---

如何根据实际情况抽象出较为贴切的层次结构；
如何将某些定性的量作比较接近实际定量化处理。

2.2 两个局限性

---

很大程度上依赖于人们的经验，主观因素的影响很大， 它至多只能排除思维过程中的严重非一致性， 却无法排除决策者个人可能存在的严重片面性。
比较、判断过程较为粗糙，不能用于精度要求较高的决策问题。

例1：

---

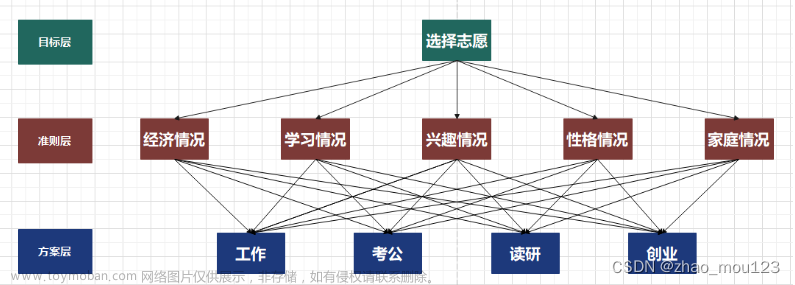
挑选合适的工作。经双方恳谈，已有三个单位表示愿意录用某毕业生。该生 根据已有信息建立了一个层次结构模型，如图所示。

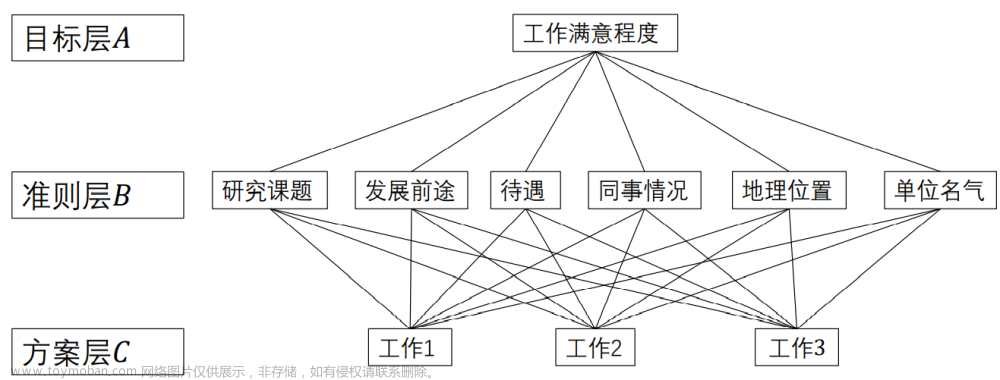
准则层的判断矩阵

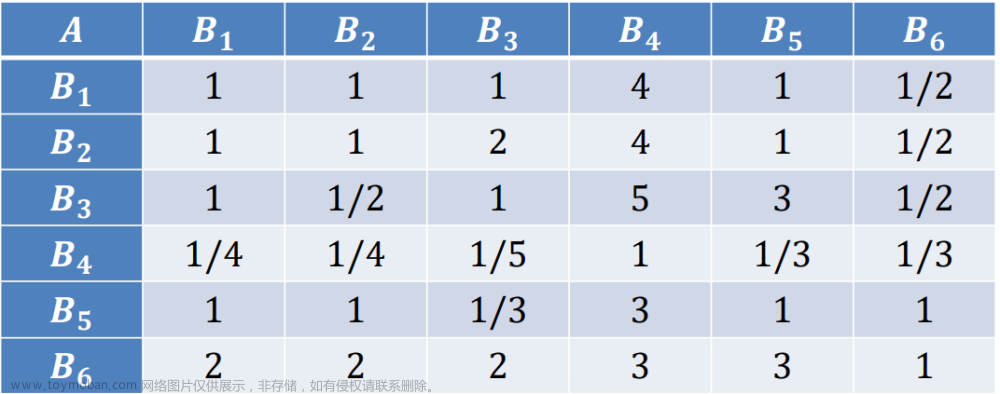
方案层的判断矩阵

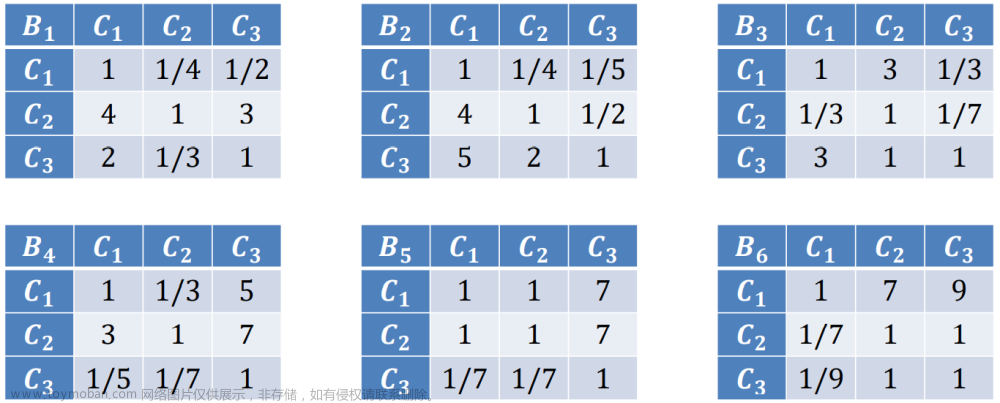
层次总排序

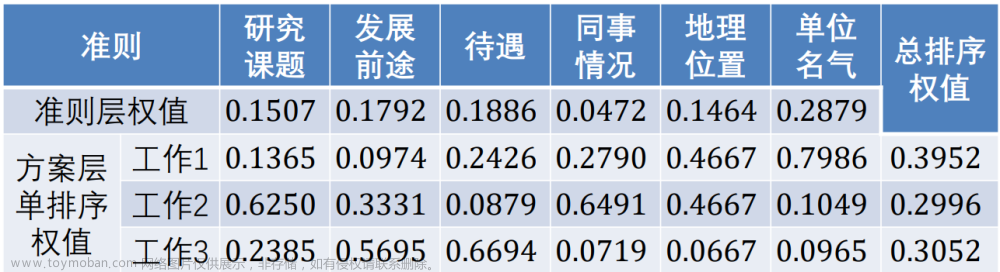
最满意的工作为工作1。

代码

我们继续把最开始的那个例子仔细分析好（这个例子的分析参考于：数模01 层次分析法_哔哩哔哩_bilibili）文章来源地址https://www.toymoban.com/news/detail-788049.html

例2：

假期旅游有3个旅游胜地𝑃1, 𝑃2, 𝑃3供你选择，试确定一个最佳地点。

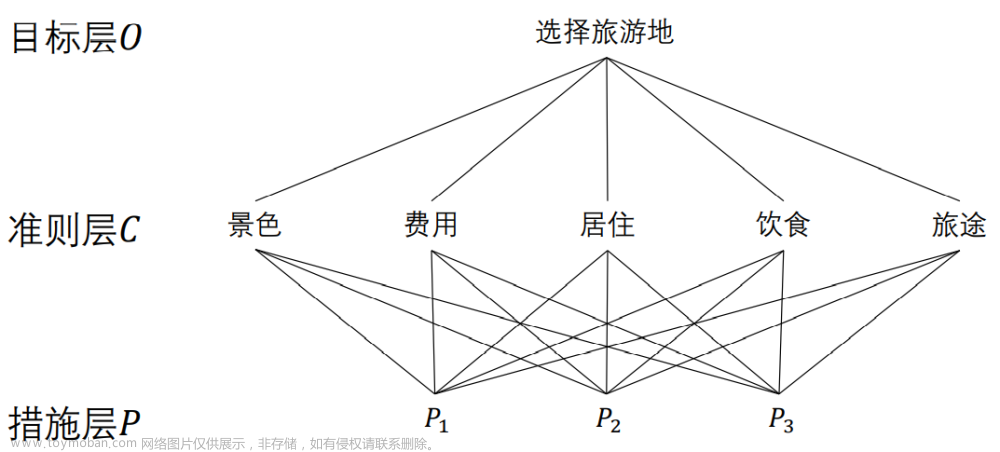
建模

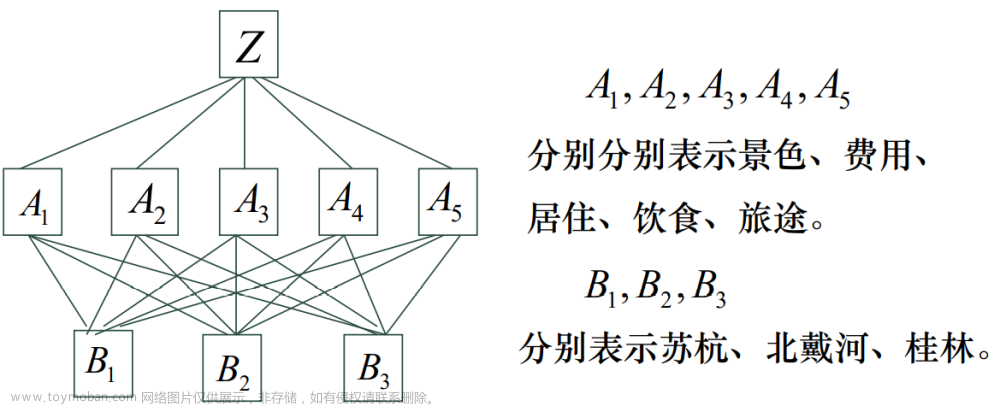
构造成对分析矩阵

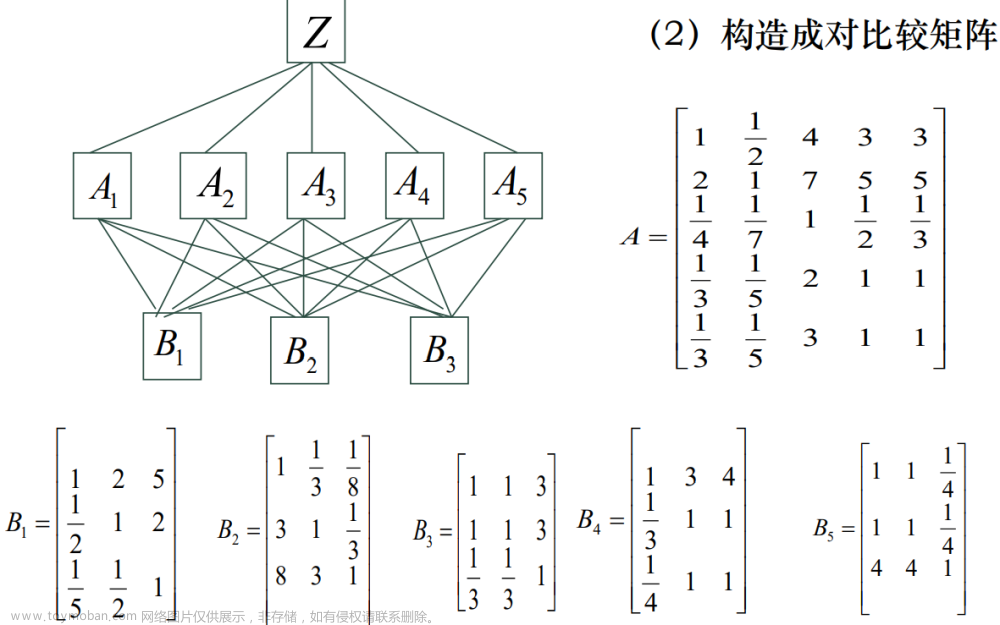
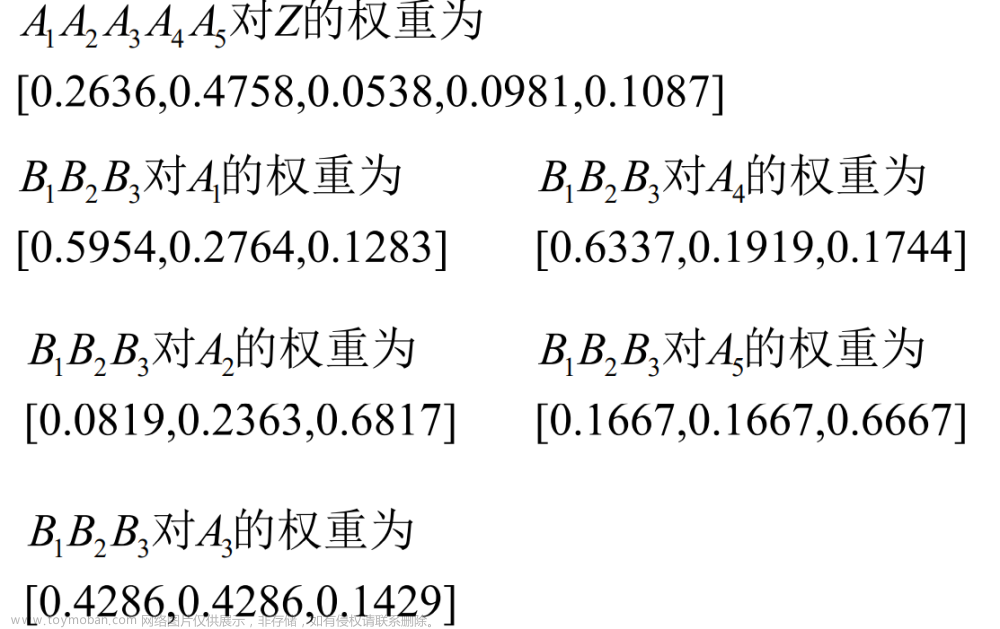
代码

disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while  k>p
  i=i+1;
  x(:,i)=A*y(:,i-1);
  m(i)=max(x(:,i));
  y(:,i)=x(:,i)/m(i);
  k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
         %以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
    disp('此矩阵的一致性可以接受!');
    disp('CI=');disp(CI);
    disp('CR=');disp(CR);
end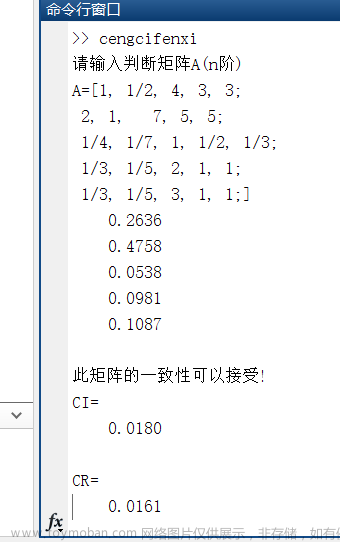

其中这个例子的矩阵可以直接复制我下面敲的

[1, 1/2, 4, 3, 3;
 2, 1,   7, 5, 5;
 1/4, 1/7, 1, 1/2, 1/3;
 1/3, 1/5, 2, 1, 1;
 1/3, 1/5, 3, 1, 1;]
[1,2,5;
1/2,1,2;
1/5,1/2,1;]
[1,1/3,1/8;
3,1,1/3;
8,3,1;]
[1,1,3;
1,1,3;
1/3,1/3,1;]
[1,3,4;
1/3,1,1;
1/4,1,1;]
[1,1,1/4;
 1,1,1/4;
 4,4,1;]